Introduction

Hepatocellular carcinoma is one of the most common malignant tumors worldwide and a leading cause of cancer-related deaths, posing a significant threat to human health1. According to data from the World Cancer Research Fund, although the growth rate of liver cancer cases has declined2, the disease burden remains high, survival rates are generally low, and treatment levels urgently need improvement. The early manifestations of liver cancer are often subtle and nonspecific, making early diagnosis and treatment crucial. Currently, doctors typically segment liver lesions based on CT image diagnoses to enhance the speed and accuracy of diagnosis and treatment. However, each CT scan usually contains dozens to hundreds of image sequences, with liver tumors varying widely in shape and size, and differences between patients adding to the complexity. This makes manual segmentation by doctors time-consuming and labor-intensive, and the process can be influenced by personal subjectivity and experience, leading to potential misdiagnoses. Therefore, there is an urgent need to propose a computer-aided diagnostic task for liver tumor segmentation in CT images to reduce clinical workload and improve diagnostic efficiency.

To advance the development of automatic segmentation tasks related to lesion regions in medical images, scholars both domestically and internationally conduct relevant research. These efforts are mainly categorized into machine learning-based methods and deep learning-based methods. Machine learning-based methods often degrade the quality of medical images, causing more blurred boundaries and making localization difficult. In contrast, deep learning-based methods can effectively extract features of the region of interest and have been widely used across various fields of medical imaging, achieving success in lung nodule detection3, skin lesion segmentation4, and more. With the FCN5 deep learning network architecture demonstrating excellent performance in segmentation tasks, the medical imaging field has also begun to improve on the FCN model, as shown in Fig. 1a. In medical image segmentation tasks, the most representative U-Net6 structure combines high-resolution and low-resolution features to effectively address the multi-scale and morphological differences of the lesion region, as depicted in Fig. 1b. However, this structure has a significant semantic gap between the encoder and decoder, making it challenging to fuse information effectively through simple skip connections. Consequently, researchers have proposed various improved U-shaped structure models, such as the one shown in Fig. 1c.

Fig. 1
figure 1

Classical model of medical image segmentation and its improvement method.

Full size image

Although existing work has achieved good results in the task of liver tumor segmentation, two significant problems remain: (1) Tumor lesions vary significantly in size. This variation complicates feature extraction, leading to potential misses or misdetections, and hampers accurate identification of the tumor ___location. (2) Blurred boundaries. The differences between the tumor region and the surrounding tissue are minimal, and the tumor boundaries are often blurred in CT images. Consequently, accurately delineating the lesion area from the liver region is challenging.

To address the problem of significant size differences in liver tumor targets, existing tumor segmentation tasks do not fully consider multi-scale contextual information and often overlook the role of feature fusion for information enhancement. Although some papers, such as ASF-YOLO7, have noted this issue and addressed it using the TPM module, they fuse features from large, medium, and small neighboring encoders directly through the channel in the middle layer. This approach does not consider the differences in the information, making it difficult to balance the fusion ratio between the various parts, thus resulting in sub-optimal fusion outcomes. To address the problem of blurred boundaries in the liver tumor region, existing papers often adopt the encoder-decoder structure represented by U-Net for liver tumor segmentation tasks. However, this approach overlooks the semantic gap between the low-level features extracted by the encoder and the high-level features produced by the decoder before fusion. Although this method supplements the subsequent segmentation process with rich, detailed information, the encoder passes through a relatively small number of convolutional layers and retains a large amount of noise information along with the detailed information. As a result, direct fusion incorporates substantial noise into the decoder, which interferes with the subsequent segmentation results.

This paper investigates improvements in two key areas to resolve the aforementioned issues. First, adaptive fusion is applied to the features of each layer of the encoder, enabling the AFFM module to adaptively select appropriate features for fusion based on the size and characteristics of the tumor in the CT image. This ensures that the detailed information at each encoder stage is fully utilized and that multi-scale information is enriched. Second, the ESGM module is proposed to use edge-aware guidance to filter noise after feature fusion and enhance edge information. The refined detail information is then fused with the semantic information from the decoder, ensuring that features with enhanced expression capabilities are utilized in the subsequent segmentation process. This method guides the segmentation model by integrating boundary information. To summarize, the contributions of this paper are threefold:

·We propose MAEG-Net, a multi-scale adaptive feature fusion network based on edge-guidance, to mitigate the effects of large tumor size variations and ambiguous boundary regions in segmentation tasks.

·An advanced adaptive feature fusion module is proposed to enhance the multi-scale expression ability of the encoder features by adaptively fusing the features of each layer using a channel partition selection mechanism. Additionally, an edge-sensing guided module is introduced to effectively capture boundary information. Simultaneously, noise filtering is applied to the detail information after feature fusion, allowing the filtered detail information to be fused with the semantic information from the decoder.

·Experimental results on the LiTS2017 dataset confirm the effectiveness of the proposed module in liver tumor segmentation tasks.

Related work

Liver tumor segmentation

In recent years, computer-aided diagnostic techniques have garnered significant attention from the medical and academic communities, and Convolutional Neural Networks (CNNs) have achieved remarkable success in medical image segmentation tasks8,9,10. Liu et al.11 proposed a spatial feature fusion convolutional network, which makes full use of multiscale feature information and adds residual structure in the downsampling process so that the spatial information can be effectively transmitted and the problem of information loss in the downsampling process can be alleviated. Jha, Debesh, et al.12 proposed to augment semantic features based on a pre-trained Pyramid Vision Transformer (PVT v2) by combining a residual upsampling module and a decoder module to generate high-quality segmentation maps. Song et al.13 introduced a hybrid convolutional network combining 2D CNNs and 3D CNNs to bridge the contextual gap, making full use of temporal information along the z-axis of CT images and retaining spatial detail information between slices, achieving good results in segmenting liver tumors in CT images. Wang et al.14 utilized a contextually parallel attention module in skip connections to narrow the codec semantic gap and increase detailed information. Hybrid dilation convolution and double dilation convolution were used in the codec stage to enhance the receptive field. Zhang et al.15 proposed the scale attention mechanism to effectively address the multiscale problem of liver and tumor segmentation. Kushnure et al.16 developed HFRU-Net to improve skip connection using local feature reconstruction and feature fusion mechanisms to represent detailed contextual information in high-level features. Although these methods achieve good results in the tumor segmentation task, they do not adequately take into account the high variability of liver tumor target sizes with uncertain locations and the ambiguity of tumor edges. Therefore, we propose a network structure that combines an adaptive multiscale feature fusion module and an edge-aware guidance module to enhance the multiscale expressiveness of the encoder features and improve boundary segmentation capability, thereby increasing the model's effectiveness.

Edge detection

As edge detection tasks continue to mature, several studies have emerged that incorporate edge detection into semantic segmentation tasks to improve segmentation accuracy. Especially in the field of medical image segmentation boundary information is utilized to compensate for the blurring of boundary information present in the image. A common method involves using boundary information to obtain additional supervised edge signals by incorporating ground truth. Lee et al.17 proposed a boundary shape-aware evaluator that includes expert-labeled boundary ground truth, providing feedback to the segmentation network based on boundary key points. Tang et al.18 introduced an edge prediction module in the network structure and incorporated additional supervised signals to train the edge enhancement network. Some studies enhance the basic features of the boundary by designing special modules in the model. Zhu et al.19 proposed a parallel architecture for semantic segmentation and edge detection, utilizing a graph convolutional network for feature fusion. Ta et al.20 proposed a boundary learning and enhancement network that recovers the edge information by constructing two new boundary modules to produce boundary information discriminative features. Bui et al.21 preserved boundary information and enhanced polyp segmentation models by combining edge detection and attention mechanisms. Le et al.22 addressed the weak boundary image segmentation problem by proposing a two-branch network structure: the first branch extracts high-level features as region information, while the second branch extracts low-level features as boundary information. An attention mechanism added to the boundary extraction branch considers the target contour as a hyperplane, using all information near the contour as supplementary boundary information.

Method

Overall architecture

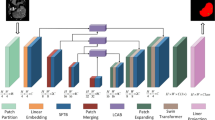
Our proposed MAEG-Net architecture consists of four main modules: encoder, decoder, adaptive feature fusion module, and edge-aware guidance module. MAEG-Net is divided into an encoder and a decoder by skip-connection. The encoder stage uses ResNet50 as the backbone network for extracting the multilevel features of the input image, denoted as \(\left\{ {{\text{F}}_{{\text{i}}} {\text{,i}} = 1,2,3,4,5} \right\}\). After that, the skip-connection of U-Net is improved by inputting each feature \({\text{F}}_{{\text{i}}}\) into the Adaptive Feature Fusion Module (AFFM), so that the neighboring low-level features and high-level features undergo adaptive multi-scale feature fusion. In addition, the integrated features pass through an Edge Sensing Guidance Module (ESGM) that extracts the edge information while noise filtering the fused detail information. Finally, the decoder stage passes the output of the feature from the hopping stage through two residual blocks consisting of \(3 \times 3\) convolutions. The overall model architecture is shown in Fig. 2.

Fig. 2
figure 2

Liver tumor segmentation network architecture (MAEG-Net).

Full size image

Encoder-Decoder stage

We improve the encoder-decoder structure using a pre-trained ResNet50 network as an encoder. The input image is fed into the pre-trained encoder to extract the image \(1/2\), \(1/4\), \(1/8\) and \(1/16\) scale information. To ensure the stability of the features, we normalize the encoder output features by employing a Batch Normalization layer to normalize each feature. The normalized \(1/16\) scale information is passed through a parallel Transformer encoder module and a null convolution module. The Transformer module23 consists of a self-attention network followed by a feed-forward neural network. Meanwhile, the dilated convolution can expand the receptive field so that the convolution contains a larger range of information. The encoder block using a combination of Transformer and dilated convolution can improve the ability of global context modeling and capture detailed information better. The dilated convolution block uses four parallel \(3 \times 3\) convolutions with the dilated rate of each layer set to 1, 3, 4, and 9, after which the four layers of features are connected through the \(1 \times 1\) convolution layer. The Transformer encoder module and the dilated convolution module outputs are connected and passed to the decoder block. The decoder is connected to the jump connection by bilinear upsampling, and the features output from the last decoder block are passed through a \(1 \times 1\) convolution layer and a Sigmoid function to generate a prediction mask map.

Adaptive feature fusion module

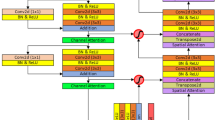
The encoder, based on ResNet50, outputs normalized feature maps at different resolutions, where low-level features are beneficial for predicting small liver tumors. However, the low-dimensional features are limited and do not provide enough contextual information, which is not very effective in the segmentation results of liver tumours. Meanwhile, after multiple downsampling, the high-dimensional features may lose the information of the small target tumour. Most of the previous medical image segmentation models24,25 up-sample the low-resolution feature maps and the up-sampled feature maps are fused with the high-resolution feature maps output by the encoder to exploit the high-level semantic information. However, this approach is still sub-optimal for objects with large size differences. To solve these problems, we propose an adaptive feature fusion strategy (e.g., Fig. 3), which selectively fuses neighboring features output from the encoder when the multiscale fusion process exists with both high- and low-dimensional features. Firstly, the high dimensional feature \(F_{l} \in R^{{H_{l} \times W_{l} \times C_{l} }}\) and low dimensional feature \(F_{s} \in R^{{H_{s} \times W_{s} \times C_{s} }}\) are initially aligned with the current middle layer feature \(F_{m} \in R^{H \times W \times C}\) by \(3 \times 3\) convolution and \(1 \times 1\) convolution, respectively, to obtain \(F_{l}^{fa} \in R^{H \times W \times C}\), \(F_{s}^{fa} \in R^{H \times W \times C}\) and \(F_{m}^{fa} \in R^{H \times W \times C}\). In order to fully capture richer independent features, feature partitioning divides the high-dimensional features, low-dimensional features, and intermediate layer features into four parts uniformly along the channel dimensions, each with the same number of channels, i.e., \(F_{l}^{d} = \left[ {l_{1} ,l_{2} ,l_{3} ,l_{4} } \right]\),\(F_{s}^{d} = \left[ {s_{1} ,s_{2} ,s_{3} ,s_{4} } \right]\),\(F_{m}^{d} = \left[ {m_{1} ,m_{2} ,m_{3} ,m_{4} } \right]\), where \(\left( {l_{i} } \right)_{i = 1}^{i = 4} \in R^{{H \times W \times \frac{C}{4}}}\) , \(\left( {s_{i} } \right)_{i = 1}^{i = 4} \in R^{{H \times W \times \frac{C}{4}}}\), \(\left( {m_{i} } \right)_{i = 1}^{i = 4} \in R^{{H \times W \times \frac{C}{4}}}\). \(l_{i}\), \(s_{i}\) , \(m_{i}\) represent the high dimensional features, low dimensional features and intermediate features of the \(i\) th partition, respectively. The four components are processed by independent convolutional processing for more fine-grained feature processing. In the presence of \(l_{i}\) or \(s_{i}\), these features are combined with \(m_{i}\) and further processed by convolutional operations to extract deeper semantic information. When both \(l_{i}\) and \(s_{i}\) are present, an adaptive fusion strategy is used to effectively fuse these two features.

Fig. 3
figure 3

Adaptive feature fusion module.

Full size image

These operations are computed as follows:

$$ \mu = Sigmoid\left( {m_{i} } \right) $$
(1)
$$ m_{i}^{\prime} = \mu \cdot s_{i} + \left( {1 - \mu } \right) \cdot l_{i} $$
(2)

where \(\mu\) denotes the value of the middle layer feature \(m_{i} \in R^{{H \times W \times \frac{C}{4}}}\) obtained by the activation function. When \(\mu > 0.5\), the model gives priority to more detailed features; when \(\mu < 0.5\), the model pays more attention to contextual features. Secondly, the result of feature-based aggregation for each partition is obtained, and the four partition features are merged in the channel dimension.

$$ F_{m}^{\prime} = \left[ {m_{1}^{\prime} ,m_{2}^{\prime} ,m_{3}^{\prime} ,m_{4}^{\prime} } \right] $$
(3)

where \(m_{i}^{\prime} \in R^{{H \times W \times \frac{C}{4}}}\) denotes the selective aggregation result for each partition. After merging \(\left( {m_{i}^{\prime} } \right)_{i = 1}^{4}\) in the channel dimension, we obtain \(F_{m}^{\prime} \in R^{H \times W \times C}\).

Since not all features after multi-scale fusion are useful information, irrelevant features may negatively affect the final segmentation accuracy. Incorporating the CBAM attention mechanism26 further filters the useful features to focus the model on important features. In addition, while multi-scale feature fusion can capture tumors of different sizes, some of the fine-grained information may be lost after fusion, especially when dealing with small tumors. Incorporating an attention mechanism allows the model to better balance global and local information. Therefore, the merged features are passed through the channel and spatial attention mechanism to adaptively learn each channel and spatial ___location information to better capture the key information. The input feature maps \(F_{m}^{\prime}\) are subjected to global max pooling and global average pooling through channel attention, followed by feeding them into a two-layer neural network MLP, respectively. The output features from the MLP are summed up and then subjected to a Sigmoid activation operation to generate the final channel attention feature, i.e., \(M_{c} \left( {F_{m}^{\prime} } \right)\).

$$ M_{c} \left( {F_{m}^{\prime} } \right) = \sigma \left( {MLP\left( {AvgPool\left( {F_{m}^{\prime} } \right)} \right) + MLP\left( {MaxPool\left( {F_{m}^{\prime} } \right)} \right)} \right) $$
(4)

where \(\sigma\) denotes the Sigmoid activation function26. A multiplication operation is done between \(M_{c} \left( {F_{m}^{\prime} } \right)\) and the input feature map \(F_{m}^{\prime}\) to generate the input features \(F_{m}^{^{\prime\prime}}\) required by the spatial attention module.

$$ F_{m}^{^{\prime\prime}} = M_{c} \left( {F_{m}^{\prime} } \right) \otimes F_{m}^{\prime} $$
(5)

where \(W_{0}\), \(W_{1}\) denote MLP weights and \(\otimes\) denotes element-by-element multiplication26. Through the spatial attention mechanism, i.e., we obtain \(M_{s} \left( {F_{m}^{^{\prime\prime}} } \right)\).

$$ M_{s} \left( {F_{m}^{^{\prime\prime}} } \right) = \sigma \left( {f^{7 \times 7} \left( {\left[ {AvgPool\left( {F_{m}^{^{\prime\prime}} } \right);MaxPool\left( {F_{m}^{^{\prime\prime}} } \right)} \right]} \right)} \right) $$
(6)

where \(\sigma\) denotes the Sigmoid activation function26. Multiply \(M_{s} \left( {F_{m}^{^{\prime\prime}} } \right)\) with the input feature map \(F_{m}^{^{\prime\prime}}\).

$$ F_{m}^{\prime \prime \prime } = M_{s} \left( {F_{m}^{\prime \prime } } \right) \otimes F_{m}^{\prime } $$
(7)

where \(f^{7 \times 7}\) denotes a convolution operation with a convolution kernel \(7 \times 7\), and \(\left[ {AvgPool\left( {F_{m}^{^{\prime\prime}} } \right);MaxPool\left( {F_{m}^{^{\prime\prime}} } \right)} \right]\) denotes splicing the average pooling and maximum pooling results along the channel. Finally, it is output by convolution. The calculation process is as follows:

$$ \tilde{F}_{m} = \delta \left( {\beta \left( {Conv\left( {F_{m}^{\prime \prime \prime } } \right)} \right)} \right) $$
(8)

where operations \(Conv()\), \(\beta ()\), and \(\delta ()\) denote convolution, BatchNorm, and ReLU, respectively, and the final output \(\tilde{F}_{m} \in R^{H \times W \times C}\).

Edge sensing guided module

Some previous papers27,28 applied edge guidance to semantic segmentation tasks, filtering noise while enhancing edge information, thus providing more useful fine-grained constraints to guide feature extraction during segmentation for accurate segmentation. Boundary ambiguity is a significant issue in medical image segmentation. Existing methods typically integrate low-level features to learn edge information, which, while useful for understanding edge features, can also introduce noise from non-edge areas. For this reason, we propose a boundary-aware guidance module (ESGM) that filters the noise information of features fused by multi-scale features while enhancing edge features. Specifically, it is shown in Fig. 4. Where \(\tilde{F}_{m}^{i}\) refers to the output features after the multi-scale adaptive feature fusion module, \(\widehat{F}_{m}^{i}\) refers to the edge features after feature extraction, and \(F_{out}\) refers to the boundary enhancement features after edge guidance.

Fig. 4
figure 4

Edge sensing guided module.

Full size image

The ESGM module consists of two main parts: 1) it provides an edge-guidance method to enhance the efficient extraction of features in jump-connected paths, and 2) it supervises the early convolutional layers using edge detection losses. In our ESGM module, the feature \(\tilde{F}_{m}^{i}\) that has been output by the multi-scale adaptive feature fusion module in 3.3 is successively passed through two \(3 \times 3\) convolution blocks. Afterwards, the output features are passed through a \(1 \times 1\) convolution block and a portion of the output is used to predict early supervised edge detection results. The other part obtains the \(\widehat{F}_{m}^{i}\) edge feature by Sigmoid function, and incorporates \(\widehat{F}_{m}^{i}\) into the original feature \(\tilde{F}_{m}^{i}\) to obtain \(F_{out}\), which is used for edge-guided features in the decoder. The process is as follows:

$$ \widehat{F}_{m}^{i} = Sigmoid\left( {Conv\left( {Conv\left( {Conv\left( {\tilde{F}_{m}^{i} } \right)} \right)} \right)} \right) $$
(9)
$$ F_{out} = \tilde{F}_{m}^{i} \times \widehat{F}_{m}^{i} + \tilde{F}_{m}^{i} $$
(10)

where, \(\times\) denotes element-by-element multiplication, \(\left( {\widehat{F}_{m}^{i} } \right)_{i = 1}^{i = 4} \in R^{H \times W \times C}\) is the edge feature after feature extraction and \(F_{out}\) denotes the boundary enhancement feature after edge guiding.

Multi-loss function

In summary, we use the joint loss consisting of segmentation loss \(L_{S}\) and boundary loss \(L_{E}\) to optimize our MAEG-Net model. The specific representation is as follows:

$$ L = \alpha L_{S} + \beta L_{E} $$
(11)

where \(L_{S}\) is derived from BCE-Dice multi-loss and \(L_{E}\) is calculated after bootstrapping by edge sensing. To achieve good results, we choose \(\alpha = 1\) , \(\beta = 0.3\). The details are as follows:

Segmentation loss

To perform liver tumor segmentation more accurately, we use a method that combines BCE Loss and Dice Loss, called the BCE-Dice Loss method. BCE Loss measures the difference between the background region and the predicted region, while Dice Loss evaluates the similarity between the actual and predicted regions. By combining these two losses, we optimize both the internal similarity and the external difference of the predicted region, resulting in improved segmentation performance. The definition is as follows:

$$ L_{S} = L_{BCE} + L_{Dice} $$
(12)

Boundary loss

We adopt a deeply supervised strategy to address the issue of fuzzy boundary information loss during the skip connection process by introducing Cross-Entropy Loss29 after each scale edge-aware bootstrap module. The definition is as follows:

$$ L_{E} = \sum\limits_{i = 1}^{4} {l_{i} } ,l_{i} = CE\left( {z_{i} ,\widehat{z}} \right) $$
(13)

where \(\left( {l_{i} } \right)_{i = 1}^{4}\) denotes multiple scale loss, \(z_{i}\) is the predicted edge mask, and \(\widehat{z}\) is the true edge mask.

Experiments and results

Experimental dataset

The proposed MAEG-Net was evaluated on the Liver Tumor Segmentation Benchmark (LiTS)30 dataset, LiTS2017, a CT dataset focusing on the liver and its tumor segmentation. This dataset, derived from the MICCAI2017 Liver Tumor Segmentation Challenge, includes data collected from seven different medical centers. It was manually reviewed by three radiologists and comprised 131 training cases and 70 test cases, each providing contrast-enhanced CT images of the patient's liver and underlying tumor. Of the 131 cases, the training set tumor labels are publicly available for download. The number of axial slices per CT scan varied, ranging from 42 to 1,026 cross-sections per volume, resulting in a total of 16,917 images. We extracted the 7,190 slices containing liver tumors. To make the slices beneficial for network training, the image intensity values were truncated to [-200,200] Hu by preprocessing to remove other irrelevant tissues. Similar to31, we used only the available training dataset (131 cases) in our experiments, which was randomly split at the patient level, with 80% training set, 10% validation set, and 10% test set.

Implementation details

Our MAEG-Net was implemented using the PyTorch deep learning framework, with all experiments conducted on two NVIDIA RTX 2080Ti GPUs. The network was trained with a batch size of 16, and the learning rate was set to 1e-4. The training was performed over 200 epochs, with an early stopping mechanism set at 50 epochs to optimize network parameter fine-tuning. To enhance network performance, we employed a joint loss function based on segmentation and edge refinement and utilized the Adam optimizer for parameter updates.

Evaluation metrics

To comprehensively evaluate the segmentation performance of the model, we utilized the Dice coefficient32, Volume Overlap Error (VOE)33, Relative Volume Difference (RVD)34, Recall35 and HD9536 metrics in this study. Among these, the Dice coefficient serves as the primary evaluation index. Here, P denotes the segmentation result produced by the proposed network, while G represents the ground truth segmentation labeled by medical professionals. The specific indexes are calculated as follows:

Dice coefficient

The Dice coefficient measures the similarity between the segmentation result and the ground truth. Its value ranges from 0 to 1, where a larger value indicates better segmentation performance.

$$ Dice\left( {P,G} \right) = \frac{{2\left| {P \cap G} \right|}}{\left| P \right| + \left| G \right|} $$
(14)

VOE

Volumetric Overlap Error, the error between the segmented volume and the ground truth volume. Its value ranges from 0 to 1, where a smaller value indicates higher segmentation accuracy.

$$ VOE\left( {P,G} \right) = 1 - \frac{{\left| {P \cap G} \right|}}{\left| P \right| \cup \left| G \right|} $$
(15)

RVD

Relative Volume Difference, mainly reacting to the segmentation results and ground truth between the over-segmentation and under-segmentation problems; the smaller the absolute value, the higher the segmentation accuracy.

$$ RVD\left( {P,G} \right) = \frac{\left| P \right| - \left| G \right|}{{\left| G \right|}} $$
(16)

Recall

Measures the ability to segment the region of interest in a segmentation experiment. A higher value indicates a higher probability that the model can segment the target region.

$$ {\text{Re}} call = \frac{TP}{{TP + FN}} $$
(17)

HD

Calculate the distance between the inferred result and the true label. HD95 is a robust version of the Hausdorff distance that more accurately reflects the differences between most boundaries by considering only the worst-case 95% of the distances. Lower HD95 values indicate more similar boundary results.

$$ d_{H} (X,Y) = \max \left\{ {\mathop {\max }\limits_{x \in X} \mathop {\min }\limits_{y \in Y} d(x,y),\mathop {\max }\limits_{y \in Y} \mathop {\min }\limits_{x \in X} d(x,y)} \right\} $$
(18)

Ablation analysis

Ablation of network complexity

To further explore the impact of network complexity on model performance, we performed ablation experiments by adjusting the number of encoders and decoders as well as adjusting the loss term parameter to assess the impact of changes in network complexity on the results of liver tumor segmentation.

Reduced network depth comparisons

We reduced the number of network encoder and decoder layers from 4 to 3 to evaluate the effect of shallow networks on the segmentation effect of liver tumors. Table 1 shows the segmentation scores, with bold indicating the best results. In particular, the Dice coefficient of the model with reduced network depth decreased by 2.1%, and the other metrics VOE and RVD likewise decreased. The results show that although the number of model parameters decreases by reducing the number of layers of encoder and decoder, which improves the computational efficiency of the model, there is a problem that the shallow network makes it difficult to adequately capture the complex information in the CT images of tumors, which affects the segmentation performance.

Table 1 Comparison of model performance with different network depths.
Full size table

Figure 5 shows the predicted liver tumor segmentation maps obtained by reducing the number of encoder and decoder blocks in the above ablation experiments. The visualized output shows that by reducing the network depth, the shallow network is unable to fully extract the deep semantic information, resulting in a degradation of the segmentation performance of the model, and the model struggles to effectively identify small target tumors in complex contexts.

Fig. 5
figure 5

Comparative visualization results of model performance at different network depths. The green area is the label and the red line is the boundary of the prediction area.

Full size image
Increase network depth comparisons

We increased the number of network encoder and decoder layers from 4 to 5 to assess whether a deeper network can improve the segmentation performance of liver tumors. However, the results from Table 1 show that after increasing the network depth, the number of parameters of the network increases to about four times of the original, but this complexity does not translate into better segmentation performance, with the Dice coefficient decreasing by 4.41%, and the evaluation metrics, VOE and RVD, decreasing in a relatively obvious way.

The visualization results of liver tumor segmentation after increasing the network depth are shown in Fig. 5. We can see that with the increase of the network depth, the segmentation effect shows a significant decrease, especially in the segmentation of small-sized tumors, the accuracy and boundary integrity of the model are reduced. This may be because deeper networks, although capable of extracting more complex multi-scale features, are overfitted due to the increase in model complexity because of the smaller liver tumor dataset. This results in inaccurate liver tumor segmentation boundaries and incorrect prediction of lesion areas.

Comparison of the effects of parameters in multiple loss terms

In our model, the loss function consists of two parts, including the segmentation loss \(L_{S}\) and the boundary loss \(L_{E}\), both of which correspond to loss term weight parameters of \(\upalpha \) and \(\upbeta \), respectively. In our experiments, \({\upalpha = 1}\) and \(\beta = 0.3\) were chosen. Since \(L_{S}\) is the main supervision for model training, keeping the \(L_{S}\) weights constant can help stabilize the model training. Therefore, we fix the value of the segmentation loss \(L_{S}\), \(\upalpha \), to 1. To assess the impact of the loss term weighting parameter, \(\upbeta \), on the model performance, we select \({\upbeta = }\left[ {0,0.1,0.3,0.5,0.7,1} \right]\), for parameter comparison experiments. The experimental results are shown in Table 2, with bold indicating the best results. When \(\upbeta \) is increased from 0 to 0.3, the Dice coefficient of the model grows from 70.48% to 71.84%, and the VOE and RVD improve accordingly. This indicates that proper enhancement of edge loss weights helps the model to capture the target region more accurately and improve the segmentation performance. When \(\upbeta \) exceeds 0.3, the performance of the model starts to decline. It is hypothesized that too high an edge loss weight may cause the model to pay too much attention to the edge features, thus ignoring the overall region accuracy. Thus, the model achieves the best performance at \({\upalpha = 1}\) and \(\beta = 0.3\).

Table 2 Comparison of model performance under different combinations of loss weight parameters.
Full size table

Module ablation

As described in the methodology mentioned in the text, the Adaptive feature fusion module (AFFM) and Edge sensing guided module (ESGM) modules are used in the backbone, the effectiveness of which is demonstrated through a series of ablation experiments. Table 3 shows the segmentation scores (Dice, VOE, and RVD). The segmentation performance is greatly improved by adding the AFFM module and ESGM module to the base model. Among them, the segmentation performance is improved by 4.29% by adding the AFFM module to adaptively fuse the multi-scale features of the encoder. The addition of the ESGM module further improves the tumor segmentation metrics with the Boundary Enhancement Assisted Task and provides additional supervision with a 4.06% improvement in segmentation performance. When the AFFM + ESGM module, MAEG-Net, is added, the performance improvement is up to 5.56%. After adding the AFFM module and ESGM module, the RVD index decreased. It is presumed that this is because the improved model is more accurate in segmenting the tumor boundary, but due to the blurring of the boundary region in the tumor image, the model is more conservative in predicting the target region overall, resulting in a low prediction region. Despite this situation, the RVD gap was not serious, and there was a relatively significant improvement in Dice, the main assessment metric. In addition, the improved model also obtained satisfactory results in HD95 and Recall assessment metrics. Therefore, the segmentation performance keeps improving with the addition of modules. The experimental results show that both AFFM and ESGM modules play a vital role in the network.

Table 3 Ablation experiment results of network structure.
Full size table

Figure 6 shows the prediction of liver tumor segmentation at baseline and with the addition of modules in the ablation experiment above. Visualization in the segmentation task shows that the baseline model segmentation is inaccurate when the liver tumor target is tiny or when the CT image tumor and tumor edges are blurred. However, the AFFM module performs better in the segmentation task for small tumors, while the ESGM module brings the edges of the tumor closer to the ground truth situation. The visualization results demonstrate the effectiveness of the proposed modules for liver tumor segmentation.

Fig. 6
figure 6

Comparison of the visualization of each module in the ablation experiment. The blue area is the label and the red line is the boundary of the prediction area.

Full size image
Effectiveness of integrating the CBAM attention mechanism into the AFFM module

To evaluate the effectiveness of incorporating the CBAM attention mechanism into the AFFM (Adaptive Feature Fusion Module), we performed ablation studies by removing the CBAM from the AFFM module. The results are presented in Table 4, where the best results are highlighted in bold. By comparing the experimental outcomes, we observed that the addition of the CBAM module led to an improvement in segmentation accuracy as measured by the Dice coefficient. Simultaneously, both the VOE and RVD metrics showed enhancements. This indicates a higher degree of correspondence between the predicted tumor regions and the ground truth, resulting in reduced discrepancies. Therefore, the introduction of the CBAM attention mechanism effectively enhances the model's performance in liver tumor segmentation tasks. It not only boosts segmentation accuracy but also reduces prediction errors, further demonstrating the pivotal role of the CBAM attention mechanism within the AFFM module.

Table 4 Results of the Attention Mechanism Ablation Experiment.
Full size table
Necessity of the fusion module under different model complexities

To evaluate the necessity of the AFFM (Adaptive Feature Fusion Module) under different model complexities, we replaced the encoder from the original ResNet50 with ResNet34 (reduced parameters) and ResNet101 (increased parameters) to observe changes in model performance. The results are shown in Table 5, with the best results highlighted in bold. From the experimental results, we can observe that when using the shallower encoder ResNet34, although the number of model parameters is reduced, the performance decreases, with the Dice coefficient dropping to 68.24%. This indicates that simply simplifying the model by reducing parameters cannot replace the effective integration of multi-scale features by the fusion module. When using the deeper encoder ResNet101, the number of model parameters increases, but the performance does not improve; the Dice coefficient decreases to 69.48%. We speculate that an encoder with too many parameters may extract excessive semantic information, thereby losing some edge and detail features important for the liver tumor segmentation task. Therefore, regardless of whether the model's number of parameters is increased or decreased, the AFFM module is irreplaceable in integrating multi-scale features and enhancing model performance.

Table 5 Performance of models combining different encoders and fusion modules.
Full size table
Comparison with other possible fusion designs

To further validate the effectiveness of the fusion module, we compared it with other possible fusion designs. We experimented with the following two methods: replacing the fusion module with simple feature concatenation and fusing multi-scale features using only the multi-head attention mechanism. The results are shown in Table 6, with the best results highlighted in bold. Under the same experimental conditions, we replaced the fusion module with simple feature concatenation and then processed the concatenated features through convolutional layers. The Dice coefficient dropped to 67.23%, representing a 4.61% decrease in performance compared to our proposed method. This indicates that simple fusion methods cannot fully capture the correlations among multi-scale features, leading to degraded model performance.

Table 6 Comparison of model performance for different fusion designs.
Full size table

Additionally, we fused the multi-scale features using only the multi-head attention mechanism, without the other components of our fusion module. The tumor segmentation Dice coefficient was 69.89%. Although this shows some improvement compared to simple fusion without attention, it is still 1.95% lower than our method. This suggests that while the multi-head attention mechanism can capture feature relationships to some extent, the method remains suboptimal. Therefore, our proposed AFFM fusion module integrates multiple attention mechanisms and adaptive fusion strategies, enabling a more comprehensive integration of multi-scale features, thereby enhancing model performance.

Impact of different convolution kernel sizes on the performance of the AFFM module

To verify the effectiveness of using \(1 \times 1\) convolutions in extracting low-dimensional features within the Adaptive Feature Fusion Module (AFFM), we conducted ablation experiments. We evaluated the processing effects of \(1 \times 1\) and \(3 \times 3\) convolution kernels on low-dimensional features in the AFFM. Specifically, we replaced the first \(1 \times 1\) convolution kernel used for processing low-dimensional features in the AFFM with a \(3 \times 3\) convolution kernel. The experimental results are presented in Table 7, with the best results highlighted in bold. The model using \(1 \times 1\) convolutions outperformed the model using \(3 \times 3\) convolutions in terms of Dice coefficient, VOE, and RVD, achieving a 3.56% increase in the Dice coefficient. This indicates that \(1 \times 1\) convolutions can effectively extract features when processing low-dimensional features, while \(3 \times 3\) convolutions did not bring significant performance improvements. We speculate that \(1 \times 1\) convolutions can aggregate channel information while keeping the spatial positions of features unchanged, thereby enhancing the model's segmentation capability. Additionally, as shown by the FLOPs and Param metrics, using \(1 \times 1\) convolutions also have advantages in computational efficiency.

Table 7 Impact of Different Convolution Kernel Sizes on Model Performance.
Full size table

Compared with other methods

To further evaluate the proposed MAEG-Net, we conducted experiments comparing it with several classical and recent medical image segmentation models on the LiTS2017 training set. These models include U-Net6, Att-UNet37, TransUNet38, TransNetR39, PVTformer12, UNeXt40, and Brau_Net +  + 41. Additionally, to more comprehensively evaluate the effectiveness of our proposed method, especially in comparison with non-U-shaped architecture models, we included the Swin Transformer42 in our experiments—an advanced non-U-shaped architecture model. We conducted all comparative experiments under the same environment and used identical hyperparameters and training configurations to ensure a fair comparison. Table 8 presents the comparison results between our proposed method and other methods. Notably, the proposed MAEG-Net achieved excellent scores (Dice: 0.7184, VOE: 0.3864, RVD: -0.1238), which can be attributed to its ability to effectively utilize multi-scale and boundary features. This shows advantages over experimental results from methods such as PVTformer and Brau_Net +  + and Swin Transformer.

Table 8 Comparison of medical image segmentation baseline models on LiTS dataset.
Full size table

PVTformer employs a pre-trained Pyramid Vision Transformer along with advanced residual upsampling, enabling more accurate capture of detailed positional and contextual feature information. It outperforms Transformer-based methods like TransNetR and TransUNet. The Brau_Net +  + model also combines Transformers and CNNs; however, compared to MAEG-Net, these two models lack edge enhancement capabilities. MAEG-Net improves upon PVTformer and Brau_Net +  + by 2.27%, 3.00%, 10.88% and 1.98%, 0.93%, 0.86% in Dice coefficient, VOE, and RVD, respectively. As an advanced non-U-shaped architecture model, Swin Transformer leverages a hierarchical Transformer architecture and a shifted window self-attention mechanism, which offers advantages in capturing multi-scale information. However, in our experiments, the performance of Swin Transformer did not surpass that of our proposed model. This may be because Swin Transformer lacks specialized enhancement for edge features, whereas MAEG-Net better captures and utilizes edge information, leading to superior segmentation performance. Specifically, MAEG-Net outperforms Swin Transformer by 1.24%, 1.03%, and 0.58% in Dice coefficient, VOE, and RVD, respectively. Although Att-UNet has the best RVD metrics, which may be attributed to its attention gate that suppresses irrelevant regions, focuses on useful salient features, helps in clustering features, and may obtain lower RVD scores. But Dice coefficient as the main evaluation metric is 7.1% higher for MAEG-Net than Att-UNet.

Figure 7 shows the visual segmentation results of the proposed network on the LiTS2017 dataset. The results show that MAEG-Net achieves higher accuracy and more precise segmentation of edges in false positive cases and fuzzy boundary locations. After the edge guidance module, the boundary region segmentation is relatively complete and closer to the ground truth. In contrast, other methods will show imprecise segmentation of the tumor lesion region and high error in tumor boundary segmentation. Especially compared with UNet and TransNetR. Overall, the proposed network can effectively segment tumors while exhibiting good performance.

Fig. 7
figure 7

Visual comparison of the proposed network with other medical segmentation baseline networks. The green area is the label and the red line is the boundary of the prediction area.

Full size image

Conclusion

In this paper, we introduce MAEG-Net, a novel architecture designed for liver tumor segmentation. Our approach leverages an advanced adaptive feature fusion module (AFFM) and an edge-aware guidance module (ESGM) to simultaneously explore multi-scale relationships and boundary information in CT images for liver tumor segmentation. The AFFM enhances the expression capability of multi-scale features by employing a channel partition selection mechanism to adaptively fuse features from each layer of the encoder. On the other hand, the ESGM module effectively filters noise, captures boundary information, and integrates with the Canny operator to provide robust supervision, thereby enhancing boundary perception. Through extensive experiments conducted on the LiTS dataset, our method demonstrates superior performance in liver tumor segmentation compared to conventional pure CNN and Transformer-based approaches.