Introduction

As a vital helicopter component, the main reducer primarily transfers the engine power to the main and tail rotors. Due to space limitations and the need for weight reduction, the main reducer in helicopters typically utilizes a gear split-torsion transmission system. While advantageous for being compact, lightweight, possessing a high transmission ratio, and ensuring high reliability, this configuration also introduces dynamic issues such as bias loads and system vibrations1,2,3.

These bias loads and vibrations arise from various sources, including external load excitations, internal time-varying meshing stiffness excitations, and error excitations. These errors encompass geometric errors, transmission errors, manufacturing errors, and installation errors. Reviewing the literature reveals that numerous studies have explored the impact of these errors on system dynamics. For instance, Dong et al.4 developed a solution algorithm applicable to spur and helical gears, achieving high accuracy between experimental and simulation results for geometric transmission errors. Zhou et al.5 analyzed the effect of centering errors on the fatigue life of herringbone gears, noting a decrease in gear life with larger errors. Donmez et al.6 created a rattle prediction model for spur gears that includes manufacturing errors like eccentricity and tooth indexing errors, discovering that tooth indexing errors significantly worsen gear rattle. Hu et al.7 introduced a nonlinear dynamics model for spur gears considering the uncertainties of multi-degree-of-freedom shaft deviations and found that shaft misalignment greatly amplifies system vibrations. Xie et al.8 proposed a torsional dynamics model for spur gears, highlighting that misalignment errors notably affect the dynamic meshing force of the system.

Enhanced load-sharing performance can significantly extend the life and improve the reliability of gear split-torsion transmission systems. Consequently, exploring the influence of various errors on the load-sharing performance of these systems is crucial. In this context, Yi9 and Hu10 formulated kinetic equations that account for transmission errors, revealing an inverse relationship between transmission errors and the load-sharing coefficient (LSC). Beyond transmission errors, numerous investigations have been conducted focusing on load-sharing in various transmission systems, factoring in manufacturing, and installation errors. For instance, Dong11 and Zhang12 studied the load-sharing characteristics of herringbone tooth planetary systems, performing sensitivity analyses on parameters. Similarly, Hu et al.13 analyzed the load sharing and dynamic load coefficient (DLC) for spur planetary gear systems. Dong et al.14 assessed the impact of parameters on the LSC in twin rotors concentric face gear power-split transmission systems (TRFGPSTS) and optimized gear system geometry for minimal mass. Liu et al.15 explored the influence of various errors on LSC in a two-stage six-branch herringbone transmission system, providing limit values for manufacturing and installation errors. Mo et al.16 developed a refined LSC solution model for a two-stage planetary gear system and analyzed its load-sharing performance. Hu et al.17 investigated load-sharing behaviors in a closed differential planetary transmission.

Manufacturing and installation errors in the components can be encapsulated into the center distance error and backlash18, which influence the system’s dynamic characteristics. Li18 and Shi19 developed mathematical models for gear backlash based on error and deformation. Yi20 and Shi21 used bifurcation diagrams, Floquet characteristic multipliers, Lyapunov exponents, phase diagrams, and Poincaré sections to quantify backlash’s impact on the system’s dynamic response. Huang et al.22 proposed fixed and fractal backlash modeling methods, finding that fixed backlash systems exhibit more pronounced nonlinear behaviors. Molaie23 and Ambaye24 studied backlash effects on system dynamics using theoretical and simulation methods, verifying backlash as a key factor in system nonlinearity. Dai et al.25 introduced center distance error (CDE) and alignment angles based on local defects in bearings and gears, investigating CDE’s impact on meshing stiffness. Li26 and Han27 explored CDE effects on system dynamics by creating three-dimensional finite element models. Zorko28 and Wei29 researched CDE’s impact on gearbox lifespan, showing that CDE consistently increases system vibration and reduces lifespan.

The performed literature survey reveals that existing research primarily focuses on the influence of manufacturing and installation errors on the dynamic characteristics of planetary gear systems within gear torsion drive systems. However, there is no comprehensive investigation of the dynamic characteristics of single-input and double-output gear split-torsion transmission systems, particularly in the context of backlash and center distance errors.

Aiming at addressing this gap, the present study develops a nonlinear dynamics model for a single-input dual-output gear torsion drive system. The study explores the effects of center distance error and backlash on the system’s dynamic characteristics by analyzing changes in LSC and DLC under various parameters. Sensitivity analysis and orthogonal test matching analysis are employed to redistribute the parameter values for a comprehensive investigation.

Dynamic modeling of gear split-torsion transmission systems

Modelling of gear split-torsion transmission systems

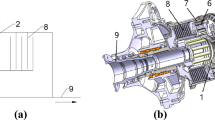
Figure 1 illustrates the structure of a single-input double-output gear split-torsion drive system. The transmission path for this configuration, which features a three-stage transmission with a single power input, is detailed as follows: The input stage bevel gear Zm meshes with Zn to change the direction of power transmission. In the split-torsion stage, the gear Zp simultaneously meshes with two gears (ZLs and ZRs) to distribute the load. The power then converges through two herringbone gears (ZLh and ZRh) in the parallel-level stage, both of which mesh with the gear ZB. Finally, the output shaft delivers the power, with a portion of the power being diverted to the tail transmission system via the tail transmission gear (ZW).

Fig. 1
figure 1

Configuration of the transmission system.

Full size image

Dynamic modeling of a gear-split torsion transmission system

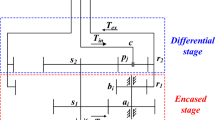
Assuming that various deformations in the system can be modeled as spring couplings, a bending-torsion coupling dynamics model was established using the concentrated parameter method, as shown in Fig. 2. In this model, the subscripts m, n, p, s, h, B, and W denote the driving bevel gear, driven bevel gear, split-torsion stage driving gear, split-torsion stage driven gear, parallel-level stage driving gear, parallel-level stage-driven gear, and tail-transfer stage driven gear, respectively. Moreover, the subscripts L and R represent the left and right shafts, respectively.

Furthermore, Knmn, KnpLs, KnpRs, KnBLh, KnBRh, and KnBW represent the meshing stiffnesses of each gear pair, KDm, Knp, KLsLh, KRsRh, and KBo denote the torsional stiffnesses of each shaft, Kmx, Kmy, and Kmz are the support stiffnesses of the power shaft, Kpx, Kpy, and Kpz represent the support stiffnesses of the input shaft, KLx, KLy, KRx, and KRy denote the support stiffnesses of the left and right shafts, KBx, KBy signify the support stiffnesses of the output shaft, KWx, KWy are the support stiffnesses of the tail transmission shaft, c is the damping value and e signifies the transmission error on the meshing line.

The meshing stiffness values of spur and herringbone gears were calculated according to the GB3480-83 involute cylindrical gear load capacity calculation method30. The meshing stiffness of bevel gears was determined using Romax Designer software. Meanwhile, the meshing damping was calculated using the following equation:

$${c_{nij}}=2{\zeta _{nij}}\sqrt {\frac{{{K_{mij}}({I_i}r_{{bi}}^{2}{I_j}r_{{bj}}^{2})}}{{{I_i}r_{{bi}}^{2}+{I_j}r_{{bj}}^{2}}}} $$
(1)

where kmij is the average meshing stiffness of the gear pair; ξnij represents the meshing damping coefficient, Ii, Ij, rbi, and rbj are the moment of inertia and the radius of the base circle of the two gears that mesh with each other, respectively.

The torsional stiffness and torsional damping of each drive shaft were determined using the following expressions:

$${K_i}=1/\sum\limits_{{k=1}}^{n} {\frac{{{l_k}}}{{G{I_{pk}}}}} $$
(2)
$${c_i}=2{\zeta _i}\sqrt {{K_i}/\left( {\frac{1}{{{I_i}}}+\frac{1}{{{I_j}}}} \right)} $$
(3)

where G is the shear modulus of the drive shaft, lk and Ipk are the length and polar moment of inertia of the kth shaft segment, respectively, ξi represents the torsional damping coefficient of the drive shaft, Ii and Ij are the moments of inertia of the two gears on the shaft.

The support stiffness of the bearing was calculated31, assuming that the support damping varies with the support stiffness. And this variation can be mathematically expressed in the form below:

$${c_{id}}={\zeta _{id}}{K_{id}}$$
(4)

where Kid is the support stiffness of the bearing, ξid represents the support damping coefficient, with an approximate range of 0.0023 to 0.025 as determined from experiments32, and the subscripts d denote the directions x, y, and z.

Fig. 2
figure 2

Dynamic model of gear transmission system.

Full size image

The dynamic meshing force of the gear pair is affected by static transmission errors, which include manufacturing and installation errors and center distance errors. In addition, the dynamic meshing force is affected by the backlash. In this paper, the backlash and CDEs of the gear pairs in the split-torsion stage and the parallel-level stage are determined mathematically to investigate their effects on the gear transmission system’s load sharing and dynamic load. In contrast, a constant value is set for the backlash and CDEs of the gear pairs in the input stage and the tail transmission stage.

The equivalent displacement of the backlash on the mesh line can be obtained using the following expression:

$$\left\{ \begin{gathered} {J_{npis}}=\frac{1}{2}{J_{wtpis}}\cos ({\alpha _{tnpis}}) \hfill \\ {J_{nBih}}=\frac{1}{2}{J_{wtBih}}\cos ({\alpha _{tnBih}})\cos {\beta _{bBih}} \hfill \\ \end{gathered} \right.$$
(5)

where Jwtpisand JwtBih represent the circumferential side clearance of the split-torsion stage and the parallel-level stage gear pair, respectively, αtnpisand αtnBih represent the end pressure angle of the split-torsion stage and the parallel-level stage gear pair, respectively, and βbBih represents the helix angle of the herringbone gear in the parallel-level stage gear pair.

As shown in Fig. 3, coordinate systems X-Y and X1-Y1 were established on a pair of meshing gears, with the center of the large gear circle On and the center of the pinion circle Om as the origins, respectively. The Y direction is oriented from On to Om. Assuming the position of the center of the large gear circle On remains unchanged, the relative displacements of the centers of the two gears can be obtained by moving the center of the pinion circle. When the pinion center moves from Om to O’m along the direction \(\varvec{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {r} }\), the center distance error Ed is obtained. The angle between OnO’m and the X-axis is denoted as α, and the meshing angle of the gear pair is denoted as αn.

Fig. 3
figure 3

Schematic diagram of center distance error.

Full size image

For a constant α angle, the relative displacement between the pinion gear and the large gear caused by the center distance error is expressed as:

$$\left\{ {\begin{array}{*{20}{l}} {\Delta {x_{mn}}=\left( {a+{E_d}} \right)\cos \left( \alpha \right)} \\ {\Delta {y_{mn}}=\left( {a+{E_d}} \right)\sin \left( \alpha \right) - a} \end{array}} \right.$$
(6)

where a is the center distance. Projecting Δxmn and Δymn onto the meshing line, the equivalent displacement en of the center distance error on the meshing line can be obtained in the form below:

$${e_n}=\Delta {x_{mn}}\cos (\zeta )+\Delta {y_{mn}}\sin (\zeta )$$
(7)

where

$$\left\{ \begin{gathered} \zeta ={\alpha _n} - \theta \hfill \\ \theta =\frac{\pi }{2} - \alpha \hfill \\ \end{gathered} \right.$$
(8)

where ζ is the angle between the meshing line and the horizontal direction, θ is the angle between OnOm and OnO’m. The equivalent displacement of the center distance error of the split-torsion stage and parallel-level stage on the corresponding meshing line can be expressed in the form below:

$$\left\{ \begin{gathered} {e_{npis}}={\kern 1pt} ({a_{pis}}+{E_{dpis}})\cos ({\alpha _{pis}}){\text{sin}}({\alpha _{npis}}+{\alpha _{pis}}) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \left[ {({a_{pis}}+{E_{dpis}})\sin ({\alpha _{pis}}) - {a_{pis}}} \right]\cos ({\alpha _{npis}}+{\alpha _{pis}}) \hfill \\ {e_{nBih}}={\kern 1pt} {\kern 1pt} ({a_{Bih}}+{E_{dBih}})\cos ({\alpha _{Bih}})\sin ({\alpha _{nBih}}+{\alpha _{Bih}}) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \left[ {({a_{Bih}}+{E_{dBih}})\sin ({\alpha _{Bih}}) - {a_{Bih}}} \right]\cos ({\alpha _{nBih}}+{\alpha _{Bih}}) \hfill \\ \end{gathered} \right.$$
(9)

where apis and aBih represent the center distance of the split-torsion stage and parallel-level stage, respectively, αnpis and αnBih denote the meshing angle of the split-torsion stage and parallel-level stage gear pair, respectively, αpis and αBih are the angle between the line connecting the centers of the meshing gears and the X-axis positively after the pinion center is shifted due to the center distance error of the split-torsion stage and parallel-level stage, respectively.

Mathematical modeling of gear split-twist transmission system

To derive the nonlinear dynamical equations of the system, a local coordinate system (denoted with asterisks) and a generalized coordinate system were established. Additionally, the coordinate system specific to the bevel gear drive was illustrated separately, as shown in Fig. 4.

Fig. 4
figure 4

Coordinate system of single-input double-output gear split-torsion transmission system

Full size image
Fig. 5
figure 5

Influence of center distance error (CDE) in different gear pairs on the load-sharing coefficient of split torsion stage (LSC-STS), load-sharing coefficient of the parallel level stage (LSC-PLS), dynamic load coefficient of split torsion stage (DLC-STS), dynamic load coefficient of the parallel level stage (DLC - PLS).

Full size image

The gear transmission system has a total of 25 generalized degrees of freedom, which can be expressed as follows:

$$\begin{gathered} \varvec{Y}=({\varphi _n},{\varphi _m},\varphi _{p}^{{}},{\varphi _{Ls}},{\varphi _{Rs}},{\varphi _{Lh}},{\varphi _{Rh}},{\varphi _D},{\varphi _B},{\varphi _o},{\varphi _w},{X_m}_{n},{Y_{mn}},{Z_{mn}},{X_{np}},{Y_{np}},{Z_{np}}, \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {X_L},{Y_L},{X_R},{Y_R},{X_B},{Y_B},{X_w},{Y_w}) \hfill \\ \end{gathered} $$
(10)

where φn, φm, φp, φis, φih, φB, and φw denote the torsional displacement of each gear, φo and φD denote the torsional displacement of the output and input power points, respectively, Xmn, Xnp, Xi, XB, and Xw denote the transversal displacements of each shaft, Ymn, Ynp, Yi, YB, and YW denote the longitudinal displacements of each shaft, Zmn and Znp denote the axial displacement.

In a transmission system, when meshing, torsional, and transverse deformations occur, projecting the displacement of each gear onto the meshing line determines the relative displacement between each pair of gears.

$$\left\{ \begin{gathered} {Y_{nmn}}={P_X}\left( { - {X_m} - {X_n}} \right) - {P_Z}\left( { - {Z_m} - {Z_n}} \right) \hfill \\ \begin{array}{*{20}{c}} {}&{} \end{array} - {P_Y}\left( { - {Y_m}+{\theta _m}{r_{pm}} - {Y_n} - {\theta _n}{r_{pn}}} \right) - {e_{nmn}} \hfill \\ {Y_{npLs}}=\left( { - Y_{p}^{ * }+{r_{bp}}{\varphi _p}} \right) - \left( {{Y_L}+{r_{bLs}}{\varphi _{Ls}}} \right) - {e_{npLs}} \hfill \\ {Y_{npRs}}=\left( { - {Y_p}+{r_{bp}}{\varphi _p}} \right) - \left( {Y_{R}^{ * }+{r_{bRs}}{\varphi _{Rs}}} \right) - {e_{npRs}} \hfill \\ {Y_{nBLh}}=\left( { - Y_{L}^{ * }+{r_{bLh}}{\varphi _{Lh}}} \right) - \left( {Y_{B}^{{}}+{r_{bB}}{\varphi _B}} \right) - {e_{nBLh}} \hfill \\ {Y_{nBRh}}=\left( { - Y_{R}^{{}}+{r_{bRh}}{\varphi _{Rh}}} \right) - \left( {Y_{B}^{ * }+{r_{bB}}{\varphi _B}} \right) - {e_{nBRh}} \hfill \\ {Y_{nBw}}=\left( { - Y_{{Bw}}^{{}}+{r_{bB}}{\varphi _B}} \right) - \left( {Y_{w}^{{}}+{r_{bw}}{\varphi _w}} \right) - {e_{nBw}} \hfill \\ \end{gathered} \right.$$
(11)

where enmn, enpis, enBih, and enBw represent the static transmission errors between each gear pair, which include center distance errors. The radii of the pitch circles for the curved bevel gears are denoted as rpm and rpn. The coefficients Px, Py, and Pz are calculation factors that can be determined as follows.

$$\left\{ \begin{gathered} {P_x}=\cos {\delta _n}\sin {\alpha _n}+\sin {\delta _n}\sin {\beta _n}\cos {\alpha _n} \hfill \\ {P_y}=\cos {\beta _n}\cos {\alpha _n} \hfill \\ {P_z}=\cos {\delta _n}\sin {\beta _n}\cos {\alpha _n} - \sin {\delta _n}\sin {\alpha _n} \hfill \\ \end{gathered} \right.$$
(12)

where δn, αn, and βn denote the pitch cone, pressure, and helix angles, respectively.

The dynamic meshing force for each gear pair can be determined by considering the meshing stiffness, the relative displacement in the gear pairs and the backlash, and is calculated as follows:

$$\left\{ \begin{gathered} {F_{nmn}}={K_{nmn}}f({Y_{nmn}},{J_{nmn}})+{c_{nmn}}\dot {f}({Y_{nmn}},{J_{nmn}}) \hfill \\ {F_{npis}}={K_{npis}}f({Y_{npis}},{J_{npis}})+{c_{npis}}\dot {f}({Y_{npis}},{J_{npis}}) \hfill \\ {F_{nBih}}=K{}_{{nBih}}f({Y_{nBih}},{J_{nBih}})+{c_{nBih}}\dot {f}({Y_{nBih}},{J_{nBih}}) \hfill \\ {F_{nBw}}={K_{nBw}}f({Y_{nBw}},{J_{nBw}})+{c_{nBw}}\dot {f}({Y_{nBw}},{J_{nBw}}) \hfill \\ \end{gathered} \right.$$
(13)

where Knmn, Knpjs, KnBih, and KnBw denote the time-varying meshing stiffness between the gear pairs, cnmn, cnpis, cnBih, and cnBw are the meshing damping between the gear pairs.

Meanwhile, f(Ynmn,Jnmn), f(Ynpis,Jnpis), f(YnBih,JnBih), and f(YnBw,JnBw) are the nonlinear function of gear backlash, which can be described by the following uniform from.

$$f(\delta n,Jn)=\left\{ \begin{gathered} \delta n - Jn{\text{ }}\delta n>Jn \hfill \\ 0{\text{ }} - Jn \leqslant \delta n \leqslant Jn \hfill \\ \delta n+Jn{\text{ }}\delta n< - Jn \hfill \\ \end{gathered} \right.$$
(14)

where δn indicates the relative displacement of gear meshing pairs, Jn represents the gear backlash of gear meshing pairs.

By decomposing the meshing force along the X and Y axes of the generalized coordinates, the components of the meshing force can be determined as follows:

$$\left\{ \begin{gathered} {F_{mx}}={F_{nmn}}\cos {\alpha _n}\sin {\beta _n}\sin {\delta _n}+{F_{nmn}}\sin {\alpha _n}\cos {\delta _n} \hfill \\ {F_{my}}={F_{nmn}}\cos {\alpha _n}\cos {\beta _n} \hfill \\ {F_{mz}}={F_{nmn}}\cos {\alpha _n}\sin {\beta _n}\cos {\delta _n} - {F_{nmn}}\sin {\alpha _n}\sin {\delta _n} \hfill \\ {F_{px}}= - {F_{npLs}}{\text{sin}}{\theta _p}+{F_{nx}}\cos {\theta _n} - {F_{ny}}\sin {\theta _n} \hfill \\ {F_{py}}={F_{npLs}}\cos {\theta _p}+{F_{npRs}}+{F_{nx}}\sin {\theta _n}+{F_{ny}}\cos {\theta _n} \hfill \\ {F_{pz}}={F_{mz}} \hfill \\ {F_{Lx}}= - {F_{nBLh}}{\text{sin}}{\theta ^*}_{L} \hfill \\ {F_{Ly}}={F_{nBLh}}\cos {\theta ^*}_{L}+{F_{npLs}} \hfill \\ {F_{Rx}}= - {F_{npRs}}{\text{sin}}{\theta ^*}_{R} \hfill \\ {F_{Ry}}={F_{npRs}}\cos {\theta ^*}_{R}+{F_{nBRh}} \hfill \\ {F_{Bx}}= - F{}_{{nBRh}}\sin {\theta _B} - {F_{nBw}}\sin {\theta _{Bw}} \hfill \\ {F_{By}}={F_{nBLh}}+F{}_{{nBLh}}\cos {\theta _B}+{F_{nBw}}\cos {\theta _{Bw}} \hfill \\ {F_{wx}}=0 \hfill \\ {F_{wy}}={F_{nBw}} \hfill \\ \end{gathered} \right.$$
(15)

In a single-rotor helicopter with a tail rotor, the main rotor experiences a reaction torque from the air as it rotates, referred to as counter torque. This counter torque can transmit as an excitation force to the helicopter’s gearbox. Concurrently, the rotation of the tail rotor generates a yawing moment, adding another external excitation to the transmission system. The counter torque from the main rotor can be calculated using an empirical formula as follows33:

$$\begin{gathered} {M_K}=nR[{P_0}+{P_b}\cos (nwt)+{P_{2b}}\cos (2nwt)+{P_{3b}}\cos (3nwt)+ \cdots \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} +{P_{mb}}\cos (mnwt)+{Q_b}\sin (nwt)+{Q_{2b}}\sin (2nwt) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} +{Q_{3b}}\sin (3nwt)+ \cdots +{Q_{mb}}\sin (mnwt)] \hfill \\ \end{gathered} $$
(16)

where n is the number of blades, R is the radius of the blades, P and Q are the amplitudes of the harmonic moments of each order, ω is the rotor excitation frequency, and t is the time variable. Since higher-order harmonic moments have a lesser excitation effect on the rotor, only the first three terms are considered33.

$${M_K}=nR[{P_0}+{P_b}\cos (nwt)+{P_{2b}}\cos (2nwt)]$$
(17)

where Pb=P2b=0.1P0 according to34. Due to the similarity in the working principles of the tail rotor and the main rotor, Eq. (17) can be slightly adjusted to calculate the yawing moment of the tail rotor.

Using the dynamics model of a single-input dual-output split-torque transmission system, the dynamic equations of the system were derived by taking into account the helicopter rotor counter-torque and the tail rotor yawing moment.

$$\left\{ \begin{gathered} {I_D}f{{\ddot {\varphi }}_D}={T_D} - {K_{Dm}}\left( {f{\varphi _D} - f{\varphi _m}} \right) - {c_{Dm}}\left( {f{{\dot {\varphi }}_D} - f{{\dot {\varphi }}_m}} \right) \hfill \\ {I_m}f{{\ddot {\varphi }}_m}={K_{Dm}}\left( {f{\varphi _D} - f{\varphi _m}} \right)+{c_{Dm}}\left( {f{{\dot {\varphi }}_D} - f{{\dot {\varphi }}_m}} \right) - {F_{ym}}{r_{pm}} \hfill \\ {m_{mx}}{{\ddot {X}}_m}={F_{mx}} - {K_{mx}}{X_m} - {c_{mx}}{{\dot {X}}_m} \hfill \\ {m_{my}}{{\ddot {Y}}_m}={F_{my}} - {K_{my}}{Y_m} - {c_{my}}{{\dot {Y}}_m} \hfill \\ {m_{mz}}{{\ddot {Z}}_m}={F_{mz}} - {K_{mz}}{Z_m} - {c_{mz}}{{\dot {Z}}_m} \hfill \\ {I_n}f{{\ddot {\varphi }}_n}={F_{yn}}{r_{pn}} - {K_{np}}\left( {f{\varphi _n} - f{\varphi _p}} \right) - {c_{np}}\left( {f{{\dot {\varphi }}_n} - f{{\dot {\varphi }}_p}} \right) \hfill \\ {I_p}f{{\ddot {\varphi }}_p}={K_{np}}\left( {f{\varphi _n} - f{\varphi _p}} \right)+{c_{np}}\left( {f{{\dot {\varphi }}_n} - f{{\dot {\varphi }}_p}} \right) - \sum\limits_{i} {{F_{npis}}{r_{bp}}} \hfill \\ \left( {{m_p}+{m_n}} \right){{\ddot {X}}_p}={F_{px}} - {K_{px}}{X_p} - {c_{px}}{{\dot {X}}_p} \hfill \\ \left( {{m_p}+{m_n}} \right){{\ddot {Y}}_p}={F_{py}} - {K_{py}}{Y_p} - {c_{py}}{{\dot {Y}}_p} \hfill \\ \left( {{m_p}+{m_n}} \right){{\ddot {Z}}_p}={F_{pz}} - {K_{pz}}{Z_p} - {c_{pz}}{{\dot {Z}}_p} \hfill \\ {I_{is}}f{{\ddot {\varphi }}_{is}}={F_{npis}}{r_{bis}} - {K_{isih}}\left( {\varphi {f_{is}} - f{\varphi _{ih}}} \right) - {c_{isih}}\left( {f{{\dot {\varphi }}_{is}} - f{{\dot {\varphi }}_{ih}}} \right) \hfill \\ {I_{ih}}f{{\ddot {\varphi }}_{ih}}={K_{isih}}\left( {f{\varphi _{is}} - f{\varphi _{ih}}} \right)+{c_{isih}}\left( {f{{\dot {\varphi }}_{is}} - f{{\dot {\varphi }}_{ih}}} \right) - {F_{nBih}}{r_{bih}} \hfill \\ \left( {{m_{ih}}+{m_{is}}} \right){{\ddot {X}}_i}={F_{ix}} - {K_{ix}}{X_i} - {c_{ix}}{{\dot {X}}_i} \hfill \\ \left( {{m_{ih}}+{m_{is}}} \right){{\ddot {Y}}_i}={F_{iy}} - {K_{iy}}{Y_i} - {c_{iy}}{{\dot {Y}}_i} \hfill \\ {I_B}f{{\ddot {\varphi }}_B}=\sum\limits_{i} {{F_{nBih}}} {r_{bB}} - {K_{Bo}}\left( {f{\varphi _B} - f{\varphi _o}} \right) - {c_{Bo}}\left( {f{{\dot {\varphi }}_B} - f{{\dot {\varphi }}_o}} \right) - {F_{nBw}}{r_{bB}} \hfill \\ {I_o}f{{\ddot {\varphi }}_o}= - {T_o}+{K_{Bo}}\left( {f{\varphi _B} - f{\varphi _o}} \right)+{c_{Bo}}\left( {f{{\dot {\varphi }}_B} - f{{\dot {\varphi }}_o}} \right) \hfill \\ {m_B}{{\ddot {X}}_B}={F_{Bx}} - {K_{Bx}}{X_B} - {c_{Bx}}{{\dot {X}}_B} \hfill \\ {m_B}{{\ddot {Y}}_B}={F_{By}} - {K_{By}}{Y_B} - {c_{By}}{{\dot {Y}}_B} \hfill \\ {I_w}f{{\ddot {\varphi }}_w}={F_{nBw}}{r_{bw}} - {T_e} \hfill \\ {m_w}{{\ddot {X}}_w}={F_{wx}} - {K_{wx}}{X_w} - {c_{wx}}{{\dot {X}}_w} \hfill \\ {m_w}{{\ddot {Y}}_w}={F_{wy}} - {K_{wy}}{Y_w} - {c_{wy}}{{\dot {Y}}_w} \hfill \\ \end{gathered} \right.$$
(18)

where mm, mn, mp, mis, mih, mB, and mw are the centralized masses of the corresponding gears, Im, In, Ip, Iis, Iih, IB, and Iw represent the rotational moment of inertia of the corresponding gears, TD, To, and Te are the input torque, rotor output load, and tail output load, respectively.

Assuming that the rotor loads and tail rotor loads account for 90% and 10% of the power consumption, respectively, and that the total transmission ratio in the tail drive shaft is 10, To and Te can be calculated using the following equation:

$$\left\{ \begin{gathered} {T_{\text{o}}}=0.9 \times 9550{i_0}{i_1}{i_2}\left( {\frac{P}{n}} \right) - {M_K} \hfill \\ {T_{\text{e}}}=0.1 \times 9550 \times 10{i_0}{i_1}{i_2}{i_3}\left( {\frac{P}{n}} \right) - {M_{KT}} \hfill \\ \end{gathered} \right.$$
(19)

where MK and MKT are the rotor counter torque and tail rotor yawing moment, respectively, P is the input power of the system, n is the input rotational speed, and i0, i1, i2, and i3 are the transmission ratios of the input stage, split-torsion stage, parallel-level stage, and tail transmission stage, respectively.

Equation (11) includes both angular and linear displacements. The angular displacement can be converted to linear displacement using the conversion equation:

$$\left\{ \begin{gathered} {Y_{Dm}}={r_{Dm}}\left( {{\varphi _D} - {\varphi _p}} \right) \hfill \\ {Y_{np}}={r_{np}}\left( {{\varphi _n} - {\varphi _p}} \right) \hfill \\ {Y_{isih}}={r_{isih}}\left( {{\varphi _{is}} - {\varphi _{ih}}} \right) \hfill \\ {Y_{Bo}}={r_{Bo}}\left( {{\varphi _B} - {\varphi _o}} \right) \hfill \\ \end{gathered} \right.$$
(20)

where YDm, Ynp, Yisih, and YBo are the torsional linear displacements, rDm, rnp, risih, and rBo are the equivalent torsional radii of the corresponding axes, respectively. Substituting Eq. (20) into Eq. (18) yields nonlinear Eqs. (21)-(26):

$$\left\{ \begin{gathered} {m_{Dmx}}{{\ddot {X}}_m}+{C_{mx}}{{\dot {X}}_m}+{K_{mx}}{X_m} - {F_{mx}}=0 \hfill \\ {m_{Dmy}}{{\ddot {Y}}_m}+{C_{my}}{{\dot {Y}}_m}+{K_{my}}{Y_m} - {F_{my}}=0 \hfill \\ {m_{Dmz}}{{\ddot {Z}}_m}+{C_{mz}}{{\dot {Z}}_m}+{K_{mz}}{Z_m} - {F_{mz}}=0 \hfill \\ {M_{npx}}{{\ddot {X}}_p}+{C_{px}}{{\dot {X}}_p}+{K_{px}}{X_p} - {F_{px}}=0 \hfill \\ {M_{npx}}{{\ddot {Y}}_p}+{C_{py}}{{\dot {Y}}_p}+{K_{py}}{Y_p} - {F_{py}}=0 \hfill \\ {M_{npz}}{{\ddot {Z}}_p}+{C_{pz}}{{\dot {Z}}_p}+{K_{pz}}{Z_p} - {F_{pz}}=0 \hfill \\ {M_L}{{\ddot {X}}_L}+{C_{Lx}}{{\dot {X}}_L}+{K_{Lx}}{X_L} - {F_{Lx}}=0 \hfill \\ {M_L}{{\ddot {Y}}_L}+{C_{Ly}}{{\dot {Y}}_L}+{K_{Ly}}{Y_L} - {F_{Ly}}=0 \hfill \\ {M_R}{{\ddot {X}}_R}+{C_{Rx}}{{\dot {X}}_R}+{K_{Rx}}{X_R} - {F_{Rx}}=0 \hfill \\ {M_R}{{\ddot {Y}}_R}+{C_{Ry}}{{\dot {Y}}_R}+{K_{Ry}}{Y_R} - {F_{Ry}}=0 \hfill \\ {m_B}{{\ddot {X}}_B}+{C_{Bx}}{{\dot {X}}_B}+{K_{Bx}}{X_B} - {F_{Bx}}=0 \hfill \\ {m_B}{{\ddot {Y}}_B}+{C_{By}}{{\dot {Y}}_B}+{K_{By}}{Y_B} - {F_{By}}=0 \hfill \\ {m_w}{{\ddot {X}}_w}+{c_{wx}}{{\dot {X}}_w}+{K_{wx}}{X_w} - {F_{wx}}=0 \hfill \\ {m_w}{{\ddot {Y}}_w}+{c_{wy}}{{\dot {Y}}_w}+{K_{wy}}{Y_w} - {F_{wy}}=0 \hfill \\ \end{gathered} \right.$$
(21)
$$\left\{ \begin{gathered} {{\ddot {Y}}_{Dm}}+\frac{{{c_{Dm}}}}{{{I_D}}}{{\dot {Y}}_{Dm}}+\frac{{{c_{Dm}}}}{{{I_m}}}{{\dot {Y}}_{Dm}}+\frac{{{K_{Dm}}}}{{{I_D}}}{Y_{Dm}}+\frac{{{K_{Dm}}}}{{{I_m}}}{Y_{Dm}} - \frac{{{T_D}{r_{Dm}}}}{{{I_D}}} - \frac{{{F_{my}}{r_{pm}}{r_{Dm}}}}{{{I_m}}}=0 \hfill \\ {{\ddot {Y}}_{np}}+\frac{{{c_{np}}}}{{{I_n}}}{{\dot {Y}}_{np}}+\frac{{{c_{np}}}}{{{I_p}}}{{\dot {Y}}_{np}}+\frac{{{K_{np}}}}{{{I_n}}}{Y_{np}}+\frac{{{K_{np}}}}{{{I_p}}}{Y_{np}} - \frac{{{F_{ny}}{r_{pn}}{r_{np}}}}{{{I_n}}} - \frac{{{F_{npLs}}{r_{bp}}{r_{np}}}}{{{I_p}}} - \hfill \\ \frac{{{F_{npRs}}{r_{bp}}{r_{np}}}}{{{I_p}}}=0 \hfill \\ {{\ddot {Y}}_{LsLh}}+\frac{{{c_{LsLh}}}}{{{I_{Ls}}}}{{\dot {Y}}_{LsLh}}+\frac{{{c_{LsLh}}}}{{{I_{Lh}}}}{{\dot {Y}}_{LsLh}}+\frac{{{K_{LsLh}}}}{{{I_{Ls}}}}{Y_{LsLh}}+\frac{{{K_{LsLh}}}}{{{I_{Lh}}}}{Y_{LsLh}} - \frac{{{F_{npLs}}{r_{bLs}}{r_{LsLh}}}}{{{I_{Ls}}}} - \hfill \\ \frac{{{F_{nBLh}}{r_{bLh}}{r_{LsLh}}}}{{{I_{Lh}}}}=0 \hfill \\ {{\ddot {Y}}_{RsRh}}+\frac{{{c_{RsRh}}}}{{{I_{Rs}}}}{{\dot {Y}}_{RsRh}}+\frac{{{c_{RsRh}}}}{{{I_{Rh}}}}{{\dot {Y}}_{RsRh}}+\frac{{{K_{RsRh}}}}{{{I_{Rs}}}}{Y_{RsRh}}+\frac{{{K_{RsRh}}}}{{{I_{Rh}}}}{Y_{RsRh}} - \frac{{{F_{npRs}}{r_{bRs}}{r_{RsRh}}}}{{{I_{Rs}}}} - \hfill \\ \frac{{{F_{nBRh}}{r_{bRh}}{r_{RsRh}}}}{{{I_{Rh}}}}=0 \hfill \\ \end{gathered} \right.$$
(22)
$$\left\{ \begin{gathered} {{\ddot {Y}}_{Bo}}+\frac{{{c_{Bo}}}}{{{I_B}}}{{\dot {Y}}_{Bo}}+\frac{{{c_{Bo}}}}{{{I_o}}}{{\dot {Y}}_{Bo}}+\frac{{{K_{Bo}}}}{{{I_B}}}{Y_{Bo}}+\frac{{{K_{Bo}}}}{{{I_o}}}{Y_{Bo}} - \frac{{{F_{nBLh}}{r_{bB}}{r_{Bo}}}}{{{I_B}}} - \frac{{{F_{nBRh}}{r_{bB}}{r_{Bo}}}}{{{I_B}}}+ \hfill \\ \frac{{{F_{nBw}}{r_{bB}}{r_{Bo}}}}{{{I_B}}} - \frac{{{T_o}{r_{Bo}}}}{{{I_o}}}=0 \hfill \\ \end{gathered} \right.$$
(23)
$$\left\{ \begin{gathered} {{\ddot {Y}}_{nmRn}}+{P_x}{{\ddot {X}}_m}+{P_x}{{\ddot {X}}_n}+{P_y}{{\ddot {Y}}_m}+{P_y}{{\ddot {Y}}_n}+{P_z}{{\ddot {Z}}_m}+{P_z}{{\ddot {Z}}_n}+{{\ddot {e}}_{nmRn}} - \frac{{{P_y}{c_{Dm}}{r_{pm}}}}{{{r_{Dm}}{I_m}}}{{\dot {Y}}_{Dm}} - \hfill \\ \frac{{{P_y}{c_{np}}{r_{pn}}}}{{{r_{np}}{I_n}}}{{\dot {Y}}_{np}} - \frac{{{P_y}{K_{Dm}}{r_{pm}}}}{{{r_{Dm}}{I_m}}}{Y_{Dm}} - \frac{{{P_y}{K_{np}}{r_{pn}}}}{{{r_{np}}{I_n}}}Y_{{pn}}^{{}}+\frac{{{P_y}{F_{my}}r_{{pm}}^{2}}}{{{I_m}}}+\frac{{{P_y}{F_{ny}}r_{{pn}}^{2}}}{{{I_n}}}=0 \hfill \\ {{\ddot {Y}}_{npLs}}+\ddot {Y}_{p}^{*}+\ddot {Y}_{L}^{{}}+{{\ddot {e}}_{npLs}} - \frac{{{c_{np}}{r_{bp}}}}{{{r_{np}}{I_p}}}{{\dot {Y}}_{np}} - \frac{{{c_{LsLh}}{r_{bLs}}}}{{{r_{LsLh}}{I_{Ls}}}}{{\dot {Y}}_{LsLh}} - \frac{{{K_{np}}{r_{bp}}}}{{{r_{np}}{I_p}}}{Y_{np}} - \hfill \\ \frac{{{K_{LsLh}}{r_{bLs}}}}{{{r_{LsLh}}{I_{Ls}}}}{Y_{LsLh}}+\frac{{{F_{npLs}}r_{{bp}}^{2}}}{{{I_p}}}+\frac{{{F_{npRs}}r_{{bp}}^{2}}}{{{I_p}}}+\frac{{{F_{npLs}}r_{{bLs}}^{2}}}{{{I_{Ls}}}}=0 \hfill \\ {{\ddot {Y}}_{npRs}}+\ddot {Y}_{p}^{{}}+\ddot {Y}_{R}^{*}+{{\ddot {e}}_{npRs}} - \frac{{{c_{np}}{r_{bp}}}}{{{r_{np}}{I_p}}}{{\dot {Y}}_{np}} - \frac{{{c_{RsRh}}{r_{bRs}}}}{{{r_{RsRh}}{I_{Rs}}}}{{\dot {Y}}_{RsRh}} - \frac{{{K_{np}}{r_{bp}}}}{{{r_{np}}{I_p}}}{Y_{np}} - \hfill \\ \frac{{{K_{RsRh}}{r_{bRs}}}}{{{r_{RsRh}}{I_{Rs}}}}{Y_{RsRh}}+\frac{{{F_{npLs}}r_{{bp}}^{2}}}{{{I_p}}}+\frac{{{F_{npRs}}r_{{bp}}^{2}}}{{{I_p}}}+\frac{{{F_{npRs}}r_{{bRs}}^{2}}}{{{I_{Rs}}}}=0 \hfill \\ {{\ddot {Y}}_{nBLh}}+\ddot {Y}_{L}^{*}+\ddot {Y}_{B}^{{}}+{{\ddot {e}}_{nBLh}} - \frac{{{c_{Bo}}{r_{bB}}}}{{{r_{Bo}}{I_B}}}{{\dot {Y}}_{Bo}} - \frac{{{c_{LsLh}}{r_{bLh}}}}{{{r_{LsLh}}{I_{Lh}}}}{{\dot {Y}}_{LsLh}} - \frac{{{K_{Bo}}{r_{bB}}}}{{{r_{Bo}}{I_B}}}{Y_{Bo}} - \hfill \\ \frac{{{K_{LsLh}}{r_{bLh}}}}{{{r_{LsLh}}{I_{Lh}}}}{Y_{LsLh}}+\frac{{{F_{nBLh}}r_{{bB}}^{2}}}{{{I_B}}}+\frac{{{F_{nBRh}}r_{{bB}}^{2}}}{{{I_B}}}+\frac{{{F_{nBLh}}r_{{bLh}}^{2}}}{{{I_{Lh}}}} - \frac{{{F_{nBw}}r_{{bB}}^{2}}}{{{I_B}}}=0 \hfill \\ \end{gathered} \right.$$
(24)
$$\left\{ \begin{gathered} {Y_{nBRh}}={Y_{nBLh}}+\left( { - {Y_R} - Y_{B}^{ * }} \right)+\left( { - {e_{nBRh}}+{e_{nBLh}}} \right)+\left( {Y_{L}^{ * }+{Y_B}} \right) - \frac{{{r_{bRh}}}}{{{r_{RsRh}}}}{Y_{RsRh}}+ \hfill \\ {\text{ }}\frac{{{r_{bLh}}}}{{{r_{LsLh}}}}{Y_{LsLh}}+\frac{{{r_{bLh}}}}{{{r_{bLs}}}}\left( {{Y_{npLs}}+Y_{p}^{ * }+{Y_L}+{e_{npLs}}} \right) - \frac{{{r_{bRh}}}}{{{r_{bRs}}}}\left( {{Y_{npRs}}+{Y_p}+Y_{R}^{ * }+{e_{npRs}}} \right) \hfill \\ \end{gathered} \right.$$
(25)
$$\left\{ \begin{gathered} {{\ddot {Y}}_{nBw}}+{{\ddot {Y}}_{Bw}}+{{\ddot {Y}}_w}+{{\ddot {e}}_{nBw}}+\frac{{{c_{Bo}}{r_{bB}}}}{{{I_B}{r_{Bo}}}}{{\dot {Y}}_{Bo}}+\frac{{{K_{Bo}}{r_{bB}}}}{{{I_B}{r_{Bo}}}}{Y_{Bo}}+\frac{{{F_{nBw}}r_{{bw}}^{2}}}{{{I_w}}} - \frac{{{F_{nBLh}}r_{{bB}}^{2}}}{{{I_B}}} - \hfill \\ \frac{{{F_{nBRh}}r_{{bB}}^{2}}}{{{I_B}}}+\frac{{{F_{nBw}}r_{{bB}}^{2}}}{{{I_B}}} - \frac{{{T_e}{r_{bw}}}}{{{I_w}}}=0 \hfill \\ \end{gathered} \right.$$
(26)

Calculation of indicators

Calculation of load-sharing coefficient

The load-sharing performance of the system is quantified by the LSC, with a larger LSC indicating poorer load-sharing performance. The dynamic equations were solved using the Runge-Kutta numerical integration method to determine the dynamic meshing force. The LSC can be calculated as follows:

$$\left\{ \begin{gathered} {\Omega _{npLs}}\left( t \right)=\frac{{2{F_{npLs}}\left( t \right)}}{{{F_{npLs}}\left( t \right)+{F_{npRs}}\left( t \right)}} \hfill \\ {\Omega _{npRs}}\left( t \right)=\frac{{2{F_{npRs}}\left( t \right)}}{{{F_{npLs}}\left( t \right)+{F_{npRs}}\left( t \right)}} \hfill \\ {\Omega _{nBLh}}\left( t \right)=\frac{{2{F_{nBLh}}\left( t \right)}}{{{F_{nBLh}}\left( t \right)+{F_{nBRh}}\left( t \right)}} \hfill \\ {\Omega _{nBRh}}\left( t \right)=\frac{{2{F_{nBRh}}\left( t \right)}}{{{F_{nBLh}}\left( t \right)+{F_{nBRh}}\left( t \right)}} \hfill \\ \end{gathered} \right.$$
(27)

where Fnpis(t) and FnBih(t) represent the elastic meshing force between the gear pair of the split-torsion stage and the parallel-level stage, respectively, and Ωnpis(t) and ΩnBih(t) represent the LSC of the gear pair of the split-torsion stage and the parallel-level stage, respectively. The LSC of the split-torsion stage and the parallel-level stage can be expressed as the maximum of the LSCs observed at the transmission stages in the respective branches.

$$\left\{ \begin{gathered} {\Omega _{nps}}\left( t \right)={\left( {{\Omega _{npLs}}\left( t \right),{\Omega _{npRs}}\left( t \right)} \right)_{\hbox{max} }} \hfill \\ {\Omega _{nBh}}\left( t \right)={\left( {{\Omega _{nBLh}}\left( t \right),{\Omega _{nBRh}}\left( t \right)} \right)_{\hbox{max} }} \hfill \\ \end{gathered} \right.$$
(28)

Calculation of dynamic load coefficient

The DLC is a crucial index for assessing the transmission smoothness of gear transmission systems, where a higher DLC indicates poorer system transmission smoothness. The DLC between each gear pair can be mathematically expressed as follows:

$$\left\{ \begin{gathered} \Psi _{{npLs}}^{{}}(t)=\frac{{{F_{npLs}}(t)}}{{F_{{npLs}}^{ * }}} \hfill \\ \Psi _{{npRs}}^{{}}(t)=\frac{{{F_{npRs}}(t)}}{{F_{{npRs}}^{ * }}} \hfill \\ \Psi _{{nBLh}}^{{}}(t)=\frac{{{F_{nBLh}}(t)}}{{F_{{nBLh}}^{ * }}} \hfill \\ \Psi _{{nBRh}}^{{}}(t)=\frac{{{F_{nBRh}}(t)}}{{F_{{nBRh}}^{ * }}} \hfill \\ \end{gathered} \right.$$
(29)

where F*npis and F*nBih represent the static meshing force between the gear pair of the split-torsion and parallel-level stages, respectively. The DLC of the split-torsion stage and the parallel-level stage can be expressed as the maximum of the DLCs observed at the transmission stage in their respective branches .

$$\left\{ \begin{gathered} {\Psi _{nps}}\left( t \right)={\left( {{\Psi _{npLs}}\left( t \right),{\Psi _{npRs}}\left( t \right)} \right)_{\hbox{max} }} \hfill \\ {\Psi _{nBh}}\left( t \right)={\left( {{\Psi _{nBLh}}\left( t \right),{\Psi _{nBRh}}\left( t \right)} \right)_{\hbox{max} }} \hfill \\ \end{gathered} \right.$$
(30)

Calculation of sensitivity

Sensitivity measures how responsive a system is to a specific factor, helping to identify key factors. The sensitivity of the LSC to each parameter is defined as11:

$$S=\left| {\frac{{({\Omega _j} - {\Omega _i})/{\Omega _i}}}{{({K_j} - {K_i})/{K_i}}}} \right| \times 100{\text{\% }}$$
(31)

where Ωj and Ωi are the LSCs corresponding to Kj and Ki, respectively. The LSC is the maximum among all LSCs in the system. Kj and Ki denote the parameter after and before the change, respectively.

Dynamic analysis of a gear split-twist transmission system

The dynamic characteristics of the single-input dual-output split-torsion transmission system are explored through the analysis of load-sharing and dynamic load coefficient evolution curves affected by center distance error and backlash. The fundamental parameters of the single-input dual-output torsional transmission system are detailed in Tables 1 and 2, and 3, maintaining a constant input power of 2000 kW and input speed of 20,900 rpm.

Table 1 Gear properties.
Full size table
Table 2 Bearing stiffness.
Full size table
Table 3 Shaft torsional stiffness.
Full size table

Influence of errors on the load sharing coefficient and dynamic load coefficient

Influence of center distance error on the load sharing coefficient and dynamic load coefficient

Figure 5 depicts the variation of the LSC and DLC with varying center distance error at each gear pair while the center distance errors at other gear pairs are set to 20 μm. Observations reveal that in the left branch, the LSCs of both the split-torsion stage and the parallel-level stage decrease gradually as the center distance error increases. Conversely, in the right branch, the LSCs of both stages increase with the center distance error. Overall, the center distance error of the parallel-level stage has a slightly larger effect on LSC than that of the split-torsion stage.

Regarding the DLCs, as the center distance error increases in the left branch, both the split-torsion stage and the parallel-level stage experience a decrease, with the split-torsion stage showing a faster decline. Conversely, in the right branch, the DLCs of both stages increase with the center distance error, with the split-torsion stage showing a faster rise. Similarly, the center distance error has a more significant effect on the DLC in the parallel-level stage compared to the split-torsion stage.

In conclusion, the load-sharing performance and transmission smoothness of the system gradually improve as the center distance error of the left branch increases, while these aspects gradually deteriorate with increasing center distance error in the right branch. In addition, the integrated dynamic characteristics of the gearing system are more sensitive to center distance errors in the parallel-level stage compared to the split-torsion stage. These errors typically arise from the manufacturing, processing, and installation of gears. Based on this analysis, it is inferred that slight manufacturing and installation errors may enhance the overall performance of the system. This also indicates that the dimensional tolerances for gears in the left ranch could be increased during the design phase to balance production costs and performance. However, the dimensional tolerances for the right ranch should remain tighter.

Fig. 6
figure 6

Influence curves of backlash (B) in different gear pairs on LSC-STS, LSC-PLS, DLC-STS, DLC - PLS.

Full size image
Fig. 7
figure 7

Relationship between the LSC and the deviation value of the center distance error.

Full size image

Influence of backlash on the load sharing coefficient and dynamic load coefficient

Figure 6 illustrates the variations in LSC and DLC as the backlash at each gear pair increases, while the backlash of the other gear pairs is maintained at a constant of 20 μm. In the left branch, the LSC of the split-torsion stage increases linearly with the backlash at the split-torsion stage, while the LSC of the parallel-level stage decreases slightly. In the right branch, as the backlash at the split-torsion stage becomes more pronounced, the LSC of the split-torsion stage initially drops to 1.002 and then increases linearly, whereas the LSC of the parallel-level stage remains relatively stable. When the backlash at the parallel-level stage in the left branch increases, the LSC of the split-torsion stage first gradually decreases to 1 and then slowly rises, while the LSC of the parallel-level stage continues to increase. Conversely, in the right branch, the LSC of the split-torsion stage increases gradually with the backlash at the parallel-level stage, and the LSC of the parallel-level stage initially drops to 1.001 and then rises linearly. Overall, the LSCs of both stages are significantly influenced by the backlash of their respective stages. The LSC at the split-torsion stage is more sensitive to backlash at the split-torsion stage than the LSC at the parallel-level stage is to backlash at the parallel-level stage.

The DLC of the split-torsion stage increases linearly with the rise in backlash at the split-torsion stage in the left branch, whereas the DLC of the parallel-level stage remains mostly unchanged. In the right branch, as backlash at the split-torsion stage gradually increases, the DLC at this stage grows slowly when the backlash is less than 40 μm, and then it rapidly increases beyond this point. The DLC at the parallel-level stage changes slightly throughout this range. When the backlash at the parallel-level stage in the left branch increases, the DLC of the split-torsion stage generally decreases but begins to rise once the backlash exceeds 150 μm. Meanwhile, the DLC at the parallel-level stage continuously increases. In the right branch, as the backlash at the parallel-level stage grows, the DLC of the split-torsion stage consistently increases, while the DLC of the parallel-level stage remains stable up to 50 μm of backlash, after which it starts to increase linearly. The DLCs of both the split-torsion and parallel-level stages are notably influenced by the backlash of their respective stages. The DLC at the split-torsion stage is slightly more sensitive to backlash at its stage compared to the sensitivity of the DLC at the parallel-level stage to its corresponding backlash. The presence of backlash leads to an increase in the system’s DLC, indicating the necessity to minimize backlash as much as possible.

Overall, the load-sharing performance of the system gradually declines as the backlash in the left branch increases, whereas in the right branch, it initially improves and then deteriorates as the backlash increases. Meanwhile, transmission instability rises with increasing backlash in either the left or the right branch. However, when the backlash in the right branch is not larger than 40 μm, the increase in transmission instability is not obvious. This observation suggests that during the design phase, the backlash in the right branch can be consciously set to a certain level, allowing for a slight reduction in gear design accuracy. In contrast, the backlash in the left branch should be minimized, and the design accuracy should be maximized.

Fig. 8
figure 8

Sensitivity curve of LSC to center distance error

Full size image
Fig. 9
figure 9

Relationship between the LSC and the deviation value of backlash

Full size image

Sensitivity analysis

In a gear split-torsion transmission system, load-sharing performance is a critical metric for evaluating the system’s effectiveness. Understanding the system’s sensitivity to each error allows for adjustments that can improve load-sharing performance to some extent.

Sensitivity analysis of center distance error

The center distance errors for all gear pairs in the left and right branches are initially set to 80–90 μm. Afterward, the center distance errors of the gear pairs in the left or right branch are increased synchronously in the split-torsion and parallel-level stages. Under different initial errors, the relationship between the LSC and the deviation value of the center distance error in the left or right branch relative to the initial error of the same branch is obtained, as shown in Fig. 7. It is observed that as the deviation values of the center distance error increase, the LSC rises gradually when the center distance error in the right branch exceeds that in the left branch. Conversely, it initially decreases and then increases when the center distance error in the left branch is greater than that in the right branch. Additionally, the LSC changes more rapidly when the center distance error in the right branch is larger compared to when the center distance error in the left branch is larger. The LSC changes even faster as the initial center distance error increases.

In summary, the load-sharing performance of the system is more sensitive to center distance errors in the right branch, and this sensitivity becomes more pronounced as the initial center distance errors increase. To achieve a reasonable load-sharing performance, a high level of accuracy in part design should be ensured to minimize the initial error. Afterward, the center distance error in the right branch can be gradually adjusted in small increments to further improve the performance of the system.

Furthermore, set the deviation value in either the left or right branch to 40% and then change the initial center distance error of all gear pairs in both the left and right branches simultaneously within a range of 20 μm to 200 μm. Then, the sensitivity curves of the LSC to the initial center distance error in the left branch or right branch are obtained, as shown in Fig. 8, which indicates that with increasing initial center distance error, the sensitivity of the LSC to these errors also increases. Initially, the LSC is more sensitive to the center distance error in the right branch, but as the error continues to rise, the sensitivity of the LSC to the center distance errors in both branches becomes similar.

Fig. 10
figure 10

Sensitivity curve of LSC to backlash.

Full size image

Sensitivity analysis of backlash

The backlash for all gear pairs in both the left and right branches is initially set to 40–45 μm as the initial error. Subsequently, the backlash of the gear pairs in either the left or right branch is increased synchronously in both the split-torsion stage and the parallel-level stage. Under these different initial errors, the relationship between the LSC and the deviation in backlash, relative to the initial error in the same branch is determined, as shown in Fig. 9. The results demonstrate that as the backlash deviation value increases, the LSC rises gradually when the backlash in the left branch exceeds that in the right branch. Conversely, the LSC initially decreases and then gradually increases when the backlash in the right branch is greater than that in the left branch. Moreover, the LSC changes more rapidly when the backlash in the right branch is larger compared to the left branch. This rate of change increases further as the initial backlash grows.

In summary, the load-sharing performance of the system is more sensitive to backlash in the right branch, and this sensitivity increases as the initial backlash grows. To ensure optimal load-sharing performance, it is crucial to maintain a high level of part accuracy during the design stage to minimize the initial error. Afterward, small incremental adjustments to the backlash in the right branch can be made to further improve system performance.

Furthermore, by setting the deviation value in either the left or right branch to 2% and varying the initial backlash of all gear pairs between 20 μm and 200 μm synchronously, the sensitivity curves of LSC to the initial backlash in each branch are obtained. Figure 10 shows that LSC demonstrates greater sensitivity to backlash in the right branch as the backlash increases.

Orthogonal test analysis

To coordinate the impact of various errors on the system’s dynamic performance, an orthogonal test parameter matching analysis was employed to identify the optimal combination of errors for achieving the best dynamic performance of the transmission system. The orthogonal test method utilized in this study is a multi-indicator orthogonal test, wherein each indicator is analyzed separately to determine the influence order of each factor on each indicator. The optimal combination of factors is then identified by comprehensively considering all indicators. The principles for selecting the optimal combination are as follows:

(1) If the indicators in the test have varying levels of importance, the optimal level of the factor should be selected based on the optimal level of the most important indicator;

(2) If the indicators are equally important, the optimal factor level should be determined by the optimal level of the most significantly affected indicator;

(3) If a factor affects multiple indicators to a similar degree, the level that appears as superior most frequently should be selected as the optimal factor level;

(4) If a factor affects all indicators but the superior levels for each indicator are different, the sum of the indicator values for each level should be compared, and the level with the smallest sum should be selected as the superior level.

In this study, the goal is to find the optimal parameter combination that minimizes the LSC and DLC values, specifically targeting the maximum LSC and DLC within the system.

Orthogonal test matching analysis of center distance error

The center distance errors of all gear pairs were set at three representative levels: -60 μm, 0 μm, and 60 μm. These factors and levels were organized into an orthogonal table L9(34) to derive the test combinations. The results of the calculations and analysis are presented in Tables 4 and 5. In these tables, the Total Value of the Indicator (TVOI) is defined as the arithmetic sum of the LSC and the DLC. This definition also applies to Table 6.

Table 4 Test combinations for the center distance error and calculations.
Full size table
Table 5 Results of analysis for the center distance error.
Full size table

Where K1, K2, and K3 represent the mean values of the indicators corresponding to levels 1, 2, and 3 in each gear pair, respectively. And R denotes the range, which is the difference between the maximum and minimum values among K1, K2, and K3 in each gear pair. The definitions of K1, K2, K3, and R apply similarly to the other tables in this section.

Based on the value of R, the degree of influence of each center distance error on LSC follows this order: LPLS > RPLS > LSTS > RSTS. Similarly, the degree of influence on DLC is in the same order: LPLS > RPLS > LSTS > RSTS. This indicates that LSC and DLC are affected by center distance error to a comparable extent. For both LSC and DLC, the smaller the value, the better the dynamic characteristics of the system. Using the multi-indicator orthogonal test method, the optimal factor levels for the independent indicators should first be identified by determining the minimum value of each indicator corresponding to each gear pair. Subsequently, the final optimal factor level can be comprehensively determined according to the selection principles. The minimum values for each indicator corresponding to each gear pair can be found in Fig. 11. Consequently, the optimal factor level for LSC is determined to be 60 μm, 60 μm, -60 μm, and − 60 μm for the center distance errors in LSTS, LPLS, RSTS, and RPLS, respectively. For DLC, the optimal factor levels are 0 μm, 60 μm, -60 μm, and − 60 μm. According to the selection principle (4), the optimal combination of center distance errors is as follows: 60 μm, 60 μm, -60 μm, and − 60 μm. In this configuration, the LSC and DLC are 1.013789 and 3.032453, respectively, resulting in a total indicator value of 4.046242. This combination represents the smallest value among 9 tests and is therefore identified as the optimal choice.

Fig. 11
figure 11

Visual diagram (CDE).

Full size image

To summarize, the load-sharing performance and transmission smoothness of the system are significantly influenced by the center distance error of the parallel-level stage. To achieve favorable dynamic characteristics of the system, it is beneficial to have a larger value for the center distance error in the left branch and a smaller value in the right branch, which means that at the design stage, the design accuracy of the left branch gear can be relaxed a bit, and the design accuracy of the right branch gear needs to be ensured, aligning with previous analyses’ conclusions. However, there is a discrepancy between the conclusions drawn from the orthogonal test and sensitivity analysis regarding which center distance error impacts the LSC the most. The orthogonal test indicates that the center distance error in the parallel-level stage of the left branch has the most significant effect on the LSC, whereas sensitivity analysis highlights different factors. This difference arises because orthogonal test matching analysis considers the coupling between center distance errors, while sensitivity analysis does not. Therefore, conducting an orthogonal test analysis remains crucial for comprehensively understanding the system’s dynamic characteristics and optimizing its performance effectively.

Orthogonal test matching analysis of backlash

Three distinct levels were chosen for all backlashes, specifically 0 μm, 10 μm, and 20 μm. Using these levels, test combinations were generated by inputting the selected factors and levels into an orthogonal table L9(34). Tables 6 and 7 present the outcomes and analysis of these calculations.

Table 6 Test combinations for the backlash and calculations.
Full size table
Table 7 Results of analysis for the backlash.
Full size table

Based on the value of R, the degree of influence of each backlash on LSC is ranked as follows: LSTS > LPLS > RSTS > RPLS. For DLC, the influence is ranked as LSTS > RPLS > RSTS > LPLS. This indicates that the LSTS has the same ranking of impacts on LSC and DLC as does RSTS, while the LPLS has the opposite ranking of impacts on LSC and DLC as does RPLS. The minimum values of each indicator for each gear pair can be found in Fig. 12. Therefore, the optimal factor level for LSC is determined to be 0 μm, 0 μm, 20 μm, and 10 μm for the backlash in LSTS, LPLS, RSTS, and RPLS, respectively. For DLC, the optimal factor levels are 0 μm, 10 μm, 0 μm, and 0 μm. Applying the selection principles (2) and (4), it is inferred that the optimal combination of backlash is 0 μm, 0 μm, 0 μm, and 0 μm. In this configuration, the LSC and DLC are 1.026767 and 2.939463, respectively, resulting in a total indicator value of 3.96623. This combination represents the smallest value among 9 tests and is therefore deemed the optimal choice.

In summary, the load-sharing performance and transmission smoothness of the system are primarily influenced by the backlash of the torsion stage in the left branch. To achieve favorable dynamic system characteristics, it is advantageous to minimize the backlash in each gear pair, which means that at the design stage, the design accuracy of each gear pair in the system needs to be ensured, aligning with previous analysis conclusions. Similarly, considering the coupling effects between the backlashes of each gear pair, the factor to which LSC is most sensitive in the orthogonal test differs from the findings of sensitivity analysis.

Fig. 12
figure 12

Visual diagram (B).

Full size image

Conclusion

This study developed and analyzed a nonlinear dynamic model for a single-input dual-output gear split-torsion transmission system. It investigated how center distance errors and backlash influence the system’s dynamic characteristics and analyzed the sensitivity of the LSC to these factors. By considering the coupling effects between center distance errors and backlashes, the study utilized orthogonal test matching analysis to identify the optimal combination of factors. The conclusions drawn from this study are summarized as follows:

(1) The dynamic behavior of the system shows completely different responses to changes of center distance errors between the left and right branches. Specifically, the system’s dynamic properties improve with increasing center distance error in the left branch, whereas they deteriorate with increasing center distance error in the right branch. Moreover, the system exhibits greater sensitivity to the center distance error of the parallel-level stage. Projecting these conclusions into the design process can be summarized by saying that the design accuracy of the left branch gear can be slightly relaxed, especially on the parallel stage, while the design accuracy of the right branch gear needs to be ensured.

(2) The dynamic characteristics of the split-torsion stage are significantly influenced by the backlash of the split-torsion stage, whereas the dynamic characteristics of the parallel-level stage are notably affected by the backlash specific to that stage. The sensitivity of the dynamic characteristics in the split-torsion stage to backlash is greater than that in the parallel-level stage. Moreover, the load-sharing performance of the system gradually deteriorates as backlash increases in the left branch, whereas it initially improves and then declines as backlash increases in the right branch. Additionally, the transmission instability of the system increases with an increase in backlash in either branch. Projecting these conclusions into the design process can be summarized by saying that the design accuracy of the gears in the right branch can be appropriately relaxed, and the design accuracy of the gears in the left branch should be as high as possible.

(3) The load-sharing performance exhibits high sensitivity to both the center distance error and backlash in the right branch. This sensitivity increases as the initial center distance error and backlash increase, which means that engineers need to ensure that the gears achieve a sufficient level of accuracy during initial design.

(4) Considering the coupling effects, the system’s dynamic characteristics are highly sensitive to the center distance error of the parallel-level stage and the backlash of the split-torsion stage, respectively. To optimize the system’s dynamic characteristics, it is recommended to minimize the center distance error in the right branch, increase the center distance error in the left branch (particularly in the parallel-level stage), and minimize the backlash in all gear pairs, which means the design accuracy of all gear pairs needs to be ensured, and mounting accuracy should also be guaranteed.