Introduction

Although noncoding RNAs1 do not encode proteins, they have many essential biological functions, especially in disease regulation. When the human body is dysregulated, noncoding RNAs can lead to various diseases, such as tumors, neurological disorders, cardiovascular diseases, and developmental abnormalities2. Noncoding RNAs are closely associated with diseases. miRNAs and lncRNAs are two important components of noncoding RNAs3,4.

miRNAs are a class of endogenously-initiated noncoding RNAs with a length of approximately 22 nucleotides (nt)5. Technical limitations have caused researchers to overlook the roles of miRNAs. It was not until the 1990s that Lee et al. discovered a small noncoding RNA of 22 nt, known as lin-14, in Caenorhabditis elegans6. Reinhart et al. further discovered that lin-4 and let-7 can bind to the 3’ untranslated region (3’ UTR) of target genes to suppress or reduce their expression levels, thereby regulating the developmental timing of C. elegans7. With the deepening research on miRNAs, more studies have demonstrated that abnormal expression of miRNAs is closely related to the onset and progression of various diseases8. For example, abnormal expression of the miR-29 family (miR-29a, miR-29b-1, miR-29b-2, and miR-29c) has been closely associated with osteoarthritis, osteoporosis, cardiorenal, and immune diseases9. Moreover, abnormal expression of miRNAs is also closely linked to cancer. Zhu et al. found that hsa-miR-21 promotes cancer cell proliferation and metastasis by inhibiting the expression of various tumor suppressor genes, especially in breast cancer10. Yanaihara et al. experimentally demonstrated that hsa-miR-155 is closely associated with lung cancer11.

LncRNAs are generally ≥ 200 nucleotides (nt) in length. LncRNAs play important roles in cell biology, including the regulation of gene expression12, chromatin structure and function13, and tumorigenesis and tumor progression14. For example, lncRNA HOTAIR is closely associated with lung cancer, promoting proliferation, survival, metastasis, and drug resistance in lung cancer cells15. Chang et al. found that lncRNA MaTAR25 plays a significant role in the proliferation and migration of breast tumor cells16. Through knockout (KO) of linc-RoR in MCF-7 cells, Peng et al. discovered that linc-RoR can promote breast cancer cell growth and activation17. Jafari et al. identified three dysregulated lncRNAs (ESRG, LINC00518, and PWRN1) in clinical samples from colorectal cancer patients18. Chakravarty et al. found that NEAT1 is a key regulator of prostate cancer19.

Therefore, predicting the associations between noncoding RNAs and diseases is profoundly important. These RNAs can serve as potential biomarkers, with their expression changes reflecting disease states and progression. Knowing these noncoding RNA-disease associations in advance can provide clinicians with crucial support for diagnostic and therapeutic decision-making20. In-depth studies of the roles of noncoding RNAs in diseases can reveal new mechanisms of disease onset and biological processes. Researchers can develop personalized medical strategies by analyzing the expression characteristics of noncoding RNAs in patients, which allows them to provide effective treatment options early. Therefore, researchers are conducting extensive and in-depth studies on the associations between miRNAs and diseases, as well as lncRNAs and diseases. These methods mainly fall into three categories: the first involves using biological experimental techniques to infer the functions of noncoding RNAs; The second method uses machine learning approaches, and the third method uses deep learning techniques.

In the early stages of noncoding RNA research, researchers primarily explored the associations between noncoding RNAs and diseases using experimental biological techniques. Chen et al. developed a qRT-PCR technique21, significantly improving detection sensitivity by specifically amplifying miRNA, allowing for accurate quantification of miRNA expression levels in various biological samples. However, this method still has issues, such as high cost. Lu et al. used microarray analysis technology to systematically map miRNAs’ expression profiles across different cancer types for the first time, providing new molecular markers for cancer classification and diagnosis22. Rinn et al. studied the function of lncRNAs in the HOX gene locus through gene knockout experiments. This study explored the role of lncRNAs in gene expression regulation23. However, gene knockout experiments are time-consuming, labour-intensive, and have a low success rate, making large-scale research challenging.

With the development of big data and biological technologies, machine learning has demonstrated strong potential in processing large datasets effectively, especially in predicting associations between miRNA-disease and lncRNA-disease. Xu et al. used Support Vector Machines (SVM) to predict associations between miRNAs and tumors by constructing a miRNA target dysregulation network24. William et al. used random forests to predict associations between miRNAs and cancer25. Xuan et al. used a weighted K-nearest neighbors (KNN) algorithm to predict miRNAs associated with human diseases26. Chen et al. developed LRLSLDA, based on the Laplacian Regularized Least Squares framework, to identify potential lncRNAs related to diseases27. The LRLSLDA model achieved an AUC value of 0.776 in leave-one-out cross-validation, laying the foundation for subsequent research on lncRNA-disease association prediction. Although machine learning can handle large datasets to some extent, it faces challenges in capturing useful information effectively, lacks sufficient accuracy, and struggles to predict miRNA-disease and lncRNA-disease associations efficiently and accurately.

Computer science, particularly artificial intelligence, has rapidly advanced in recent years. As an important branch of artificial intelligence, deep learning has introduced new approaches for predicting associations between miRNA-disease and lncRNA-disease. Deep learning can learn complex nonlinear relationships and data representations through multi-layer neural network structures. Researchers have used deep learning to represent the features of noncoding RNAs and diseases, capturing useful information to achieve more accurate predictions. Liu et al. proposed the SMALF model, which utilizes a stacked autoencoder to integrate latent features of miRNAs and diseases, extracting feature vectors for miRNA-disease associations, and uses XGBoost to predict unknown miRNA-disease associations28. Ji et al. introduced the SVAEMDA model, which employs a variational autoencoder to predict miRNA-disease associations29. Xuan et al. developed the CNNLDA model, which uses a dual convolutional neural network with an attention mechanism to predict lncRNA-disease associations30. Guo et al. proposed the LDASR computational method, which constructs feature vectors for lncRNA-disease pairs by integrating Gaussian interaction profile kernel similarity for lncRNAs, disease semantic similarity, and Gaussian interaction profile kernel similarity and uses an autoencoder to reduce feature dimensionality for predicting lncRNA-disease associations31.

More and more researchers have been integrating neural networks with graph structures to capture useful information better and extract embedding vectors, aiming to achieve better predictive performance. Zhang et al. proposed the AGAEMD model, which uses a node-level Attention Graph Auto-Encoder to integrate the graph attention mechanism into the autoencoder for predicting unknown miRNA-disease associations32. Chen et al. combined graph autoencoder and self attention mechanism to predict the associations between miRNAs and diseases33. Li et al. fused multiple sources of information and used graph attention networks to predict miRNA -disease associations34. Jin et al. employed a graph attention mechanism and multiple adaptive modalities to predict associations between miRNAs and diseases35. Liao et al. introduced GCNA-MDA, which primarily uses a GCN to capture the topological information of the disease network and uses an autoencoder to extract features of miRNA-disease associations36. Lan et al. used Principal Component Analysis (PCA) to reduce noise in the raw data, employed a Graph Attention Network (GAT) to extract useful information from lncRNAs and diseases, and utilized a Multi-Layer Perceptron (MLP) to infer lncRNA-disease associations37. Shi et al. predicted lncRNA-disease association by constructing a heterogeneous graph neural network.Wang et al.38. Li et al. used a node adaptive graph transformer with structural encoding for predicting lncRNA-disease associations39. Wang et al. proposed a method based on Graph Attention Networks (GAT) to identify associations between lncRNAs and diseases40. Zhao et al. constructed lncRNA gene disease-related heterogeneous structures to predict lncRNA-disease associations41. Li et al. used a graph autoencoder to predict the associations between cricRNAs and diseases42. Sheng et al. used graph contrastive learning to predict associations among miRNAs, lncRNAs, and diseases43.

Although researchers have proposed many methods for noncoding RNA prediction, several significant challenges still exist. First, the accuracy remains insufficient, making it difficult to accurately predict the associations between noncoding RNAs and diseases. Second, miRNAs and lncRNAs have close associations with diseases, but most experimental methods cannot fully integrate, extract, and utilize the information among miRNAs, lncRNAs, and diseases. Third, most current models treat miRNA-disease and lncRNA-disease associations separately, making it impossible to predict multiple associations simultaneously.

To address the mentioned challenges, this study proposes a method that integrates the information among miRNAs, lncRNAs, and diseases using a multigraph contrastive learning model enhanced with a GCN called K-MGCMLD. This model enables multi-association predictions, including miRNA-disease, lncRNA-disease, and lncRNA-miRNA associations, all within a single framework. The main steps of K-MGCMLD are as follows:

The first step is the construction of a heterogeneous graph. This study constructs a lncRNA-miRNA-disease heterogeneous graph by integrating similarity and association information among miRNAs, lncRNAs, and diseases. The process then involves subjecting the heterogeneous graph to data augmentation and corruption.

The second step involves downsampling using the K-means clustering algorithm to balance the positive and negative samples, allowing the model to learn more effectively.

The third step is to use an encoder with a GCN architecture to extract embedding vectors. The embedding vectors can better capture the graph’s latent topological features through multigraph contrastive learning—utilizing both local and global graph contrastive learning.

In the fourth step, this study reconstructs features using the balanced positive and negative samples and the embedding vectors, which they feed into an XGBoost classifier for classification prediction.

Methods

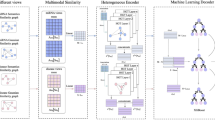
The core idea of the proposed K-MGCMLD is to integrate information among miRNAs, lncRNAs, and diseases to predict their associations. The K-MGCMLD model is composed of four parts: A, B, C, and D. In Fig. 1-A, the model integrates similarity and association information between miRNAs, lncRNAs, and diseases to construct a lncRNA-miRNA-disease (MLD) heterogeneous graph. The heterogeneous graph structure more intuitively represents the associations among multiple entities, facilitating the processing of complex relationships among different entities. By leveraging information from various nodes and edges, the model can better learn and capture more critical feature information, enhancing the model’s understanding of data details and achieving more refined feature representations. The MLD heterogeneous graph is then subjected to data augmentation and corruption, generating MLD-A and MLD-C. This step allows for more effective contrastive learning in subsequent stages, improving the model’s generalization capability and robustness, thereby enhancing the quality of feature learning.

In Fig. 1-B, the multigraph contrastive learning component applies a self-supervised learning approach to process the graph structure and its features. This self-supervised learning method does not require a large amount of labeled data. It relies only on the intrinsic structure of the data to generate training signals, significantly reducing the need for labeled data. By utilizing multigraph contrastive learning, the model can fully exploit unlabeled graph data for training, improving its representation capabilities and performance. By contrasting different views, the model can capture multi-level information within the graph and extract more enriched and meaningful embedding vectors from the heterogeneous graph. This method effectively captures multi-scale information in the graph, including local node-level information and global graph-level structure, enhancing the model’s understanding of graph-structured data.

Figure 1-C presents the unsupervised feature extraction process using an autoencoder. The process retains the features of all positive samples and applies K-means clustering to the negative sample features. From these clusters, the process uniformly extracts an equal number of negative samples from different clusters to match the number of positive samples. This approach helps balance the positive and negative samples, reducing bias and preventing the model from favoring the majority class, which ultimately helps to enhance the model’s performance.

Figure 1-D involves feature reconstruction and multi-association Prediction. K-MGCMLD is capable of performing single-association prediction and multi-association Prediction. Using multigraph contrastive learning, we extract low-dimensional embedding feature vectors denoted as Z. We reconstruct these features for miRNA-disease, lncRNA-disease, and lncRNA-miRNA associations using the sample indices balanced by the K-means clustering. Finally, we feed the reconstructed features into multiple classifiers (including MLP, XGBoost, AdaBoost, Logistic Regression, KNN, and Decision Tree) to predict miRNA-disease associations, lncRNA-disease associations, and lncRNA-miRNA interactions.

Fig. 1
figure 1

Flowchart of the K-MGCMLD model. (A) Includes the construction of the heterogeneous graph, data augmentation, and data corruption. (B) Involves using a GCN-integrated graph encoder to extract embeddings and training the model using a self-supervised learning approach with both local and global graph contrastive learning. (C) Uses an autoencoder and the K-means algorithm to balance positive and negative samples. (D) Performs feature reconstruction based on the balanced samples to predict associations among miRNA, lncRNA, and diseases. The Multigraph Contrastive Learning Algorithm is presented as shown in the Table 1:

Full size image
Table 1 Multigraph contrastive learning algorithm.
Full size table

Dataset introduction and balanced dataset

To predict associations among miRNAs, lncRNAs, and diseases, it is necessary to gather association and self-correlation information among these entities. In this study, we used the dataset published by Fu et al.44, which includes 495 human miRNAs, 240 human lncRNAs, and 405 diseases. In addition, it contains 13,559 experimentally validated miRNA-disease associations, 2,687 lncRNA-disease associations, and 1,002 lncRNA-miRNA interactions. This is shown in Table 2.

Table 2 Dataset overview.
Full size table

This study treats known miRNA-disease associations, lncRNA-disease associations, and lncRNA-miRNA interactions as positive samples. Due to the limited number of positive samples, the model might struggle to learn the associations between the positive sample features effectively.

To address this, we first retain all positive samples (i.e., known associations), then use an autoencoder to extract low-dimensional embedding feature vectors. The model then uses the low-dimensional embeddings for feature reconstruction based on the remaining negative samples. Finally, the K-means algorithm clusters all the reconstructed negative sample features. Based on the clustering results, an equal number of negative samples are uniformly extracted from each cluster, ensuring that the total number of negative samples matches the number of positive samples, thereby balancing the positive and negative samples.

Construction of the heterogeneous graph

When studying the complex relationships among miRNAs, lncRNAs, and diseases, constructing a heterogeneous graph can effectively represent these biological entities and their interactions.

Before constructing the heterogeneous graph, we first employed six fundamental matrices: the miRNA similarity matrix, lncRNA similarity matrix, disease similarity matrix, miRNA-disease association matrix, lncRNA-miRNA interaction matrix, and lncRNA-disease association matrix.

\(\:{A}_{\text{miRNA}}\in\:{\mathbb{R}}^{{n}_{m}\times\:{n}_{m}}\:\) represents the similarity adjacency matrix between miRNA nodes, where \(\:{n}_{m}\)is the number of miRNA nodes;\(\:{A}_{\text{lncRNA}}\in\:{\mathbb{R}}^{{n}_{l}\times\:{n}_{l}}\:\) represents the similarity adjacency matrix between lncRNA nodes, where \(\:{n}_{l}\)is the number of lncRNA nodes;\(\:{A}_{\text{disease}}\in\:{\mathbb{R}}^{{n}_{d}\times\:{n}_{d}}\:\) represents the similarity adjacency matrix between disease nodes, where \(\:{n}_{d}\)is the number of disease nodes;\(\:{R}_{md}\in\:\{\text{0,1}{\}}^{{n}_{m}\times\:{n}_{d}}\)represents the association matrix between miRNAs and diseases.

\(\:{R}_{ld}\in\:\{\text{0,1}{\}}^{{n}_{l}\times\:{n}_{d}}\)represents the association matrix between lncRNAs and diseases, and \(\:{R}_{ml}\in\:\{\text{0,1}{\}}^{{n}_{m}\times\:{n}_{l}}\) represents the association matrix between miRNAs and lncRNAs.

To extract as much useful information as possible from known associations to predict unknown associations, we use the six matrices mentioned above to reconstruct a heterogeneous graph that includes the associations among miRNAs, lncRNAs, and diseases. We first define different types of nodes and construct edges between nodes using the six datasets. The heterogeneous graph comprises relationships between different types of nodes, representing the similarities and associations among these nodes.

First, we define three sets of nodes:

The miRNA node set, denoted as \(\:\:{V}_{miRNA}\); The lncRNA node-set, denoted as \(\:{V}_{lncRNA}\); The disease node set, denoted as \(\:{V}_{disease}\).These nodes form the fundamental node sets within the heterogeneous graph. Next, we need to construct edges between the nodes. The model categorizes the edges into two main types: similarity edges between nodes of the same type and association edges between nodes of different types.

Similarity edges between nodes of the same type include miRNA similarity edges, lncRNA similarity edges, and disease similarity edges.

miRNA Similarity Edge: the model establishes similarity edges between miRNA nodes based on the miRNA similarity dataset. If the similarity between two miRNA nodes exceeds a threshold of 0, an edge is established between them, represented as:

$${E_{{{\text{miRNA - miRNA}}}} = \left\{ {\left( {i,j} \right)i,j \in V_{{{\text{miRNA}}}} ,{\text{similarity}} > 0} \right\}}$$
(1)

lncRNA Similarity Edge: Similarity edges are established between lncRNA nodes based on the lncRNA similarity dataset. If the similarity between two lncRNA nodes exceeds a threshold of 0, an edge is established between them, represented as:

$${E_{{{\text{lncRNA - lncRNA}}}} = \left\{ {\left( {k,l} \right)k,l \in V_{{{\text{lncRNA}}}} ,{\text{similarity}} > 0} \right\}}$$
(2)

disease Similarity Edge: Similarity edges are established between disease nodes based on the disease similarity dataset. If the similarity between two disease nodes exceeds a threshold of 0, an edge is established between them, represented as:

$${E_{{{\text{disease - disease}}}} = \left\{ {\left( {m,n} \right)m,n \in V_{{{\text{disease}}}} ,{\text{similarity}} > 0} \right\}}$$
(3)

Association edges between different nodes include miRNA-disease association edges, lncRNA-disease association edges, and lncRNA-miRNA interaction edges.

miRNA-disease Association Edge: The miRNA-disease association dataset establishes Association edges between miRNA and disease nodes. If there is an association between miRNA\(\:\:i\) and disease \(\:m\), an edge is established between them, represented as:

$${E_{{{\text{miRNA - disease}}}} = \left\{ {\left( {i,m} \right)i \in V_{{{\text{miRNA}}}} ,m \in V_{{{\text{disease}}}} ,A_{{{\text{miRNA - disease}}}} \left[ {i,m} \right] = 1} \right\}}$$
(4)

lncRNA-Disease Association Edge: The lncRNA-disease association dataset establishes Association edges between lncRNA and disease nodes. If there is an association between lncRNA \(\:k\) and disease \(\:m\), an edge is established between them, represented as:

$${E_{{{\text{lncRNA - disease}}}} = \left\{ {\left( {k,m} \right)k \in V_{{{\text{lncRNA}}}} ,m \in V_{{{\text{disease}}}} ,A_{{{\text{lncRNA - disease}}}} \left[ {k,m} \right] = 1} \right\}}$$
(5)

lncRNA-miRNA Interaction Edge: Association edges are established between miRNA and lncRNA nodes based on the lncRNA-miRNA interaction dataset. If there is an association between miRNA\(\:\:i\) and lncRNA \(\:k\), an edge is established between them, represented as:

$${E_{{{\text{lncRNA - miRNA}}}} = \left\{ {\left( {i,k} \right)i \in V_{{{\text{miRNA}}}} ,k \in V_{{{\text{lncRNA}}}} ,A_{{{\text{lncRNA - miRNA}}}} \left[ {i,k} \right] = 1} \right\}}$$
(6)

Finally, we use the adjacency matrix \(\:MLD\) to represent the entire heterogeneous graph structure. Assuming the total number of nodes is \(\:N\), \(\:MLD\) is an \(\:N\times\:N\)matrix. For edges between nodes of the same type, the matrix element \(\:{MLD\:}_{ij}\)represents the similarity value between node\(\:\:i\:\) and node \(\:j\). For edges between nodes of different types, the matrix element \(\:{MLD\:}_{ij}\)=1 indicates that an association exists, whereas \(\:{MLD\:}_{ij}\)=0 indicates that no association exists.

$$\:\begin{array}{c}MLD=\left[\begin{array}{ccc}{A}_{miRNA}&\:{R}_{ml}&\:{R}_{md}\\\:{R}_{ml}^{T}&\:{A}_{lncRNA}&\:{R}_{ld}\\\:{R}_{md}^{T}&\:{R}_{ld}^{T}&\:{A}_{disease}\end{array}\right]\end{array}$$
(7)
$$\:\begin{array}{c}V={V}_{\text{miRNA}}\cup\:{V}_{\text{lncRNA}}\cup\:{V}_{\text{disease}}\end{array}$$
(8)
$$\begin{array}{*{20}{c}} {E={{\text{E}}_{{\text{miRNA-miRNA}}}} \cup {{\text{E}}_{{\text{lncRNA-lncRNA}}}} \cup {{\text{E}}_{{\text{disease-disease}}}} \cup {{\text{E}}_{{\text{lncRNA-miRNA}}}} \cup {{\text{E}}_{{\text{miRNA-disease}}}} \cup {{\text{E}}_{{\text{lncRNA-disease}}}}} \end{array}$$
(9)

The heterogeneous graph constructed in this way can effectively integrate the similarity and association data of miRNAs, lncRNAs, and diseases, providing a foundation for further tasks such as graph embedding extraction and graph contrastive learning.

Constructing contrastive learning views

In existing research, there are various data augmentation methods, each differing by ___domain. Common data augmentation techniques in computer vision include random rotation, color jitter, and random cropping. Researchers often use techniques such as synonym replacement and random word swapping in natural language processing. The field of bioinformatics, however, is different from these domains, as mentioned earlier. In the heterogeneous graph of lncRNA-miRNA-disease associations, each association is represented by specific numerical values, making these conventional data augmentation methods unsuitable for direct application in this context.

In this study, we primarily use random dropout and Gaussian noise addition as data augmentation techniques to generate positive sample views for the next step, which is graph contrastive learning. The model is trained to make accurate predictions even in the presence of missing information or noisy data by employing random dropout and Gaussian noise addition. This helps the model become more robust when dealing with uncertainty and noise in real-world data. During training, such data augmentation methods encourage the model to learn more useful information from the heterogeneous lncRNA-miRNA-disease graph structure. This is because the model is required to maintain consistency across multiple views, which allows it to capture the essential characteristics of the data. As a result, the model better understands the intrinsic structure and features of the data, leading to greater robustness, reduced overfitting, and improved generalization capability.

$${MLD,X\xrightarrow{{Data~Augmentation}}\left( {MLD - A,\hat{X}_{1} } \right)}$$
(10)

In addition to positive samples, graph contrastive learning also requires negative samples. Therefore, besides performing data augmentation on the heterogeneous graph to generate positive sample views, we also apply data corruption to the heterogeneous graph to generate negative sample views. In this process, we use a corruption function to perturb and disrupt all association information in the original heterogeneous graph while keeping the node information unchanged. This results in a corrupted graph, which maintains the same nodes but has completely different associations than the original graph and serves as the negative sample view for graph contrastive learning.

$${MLD,X\xrightarrow{{Data~Corruption}}\left( {MLD - C,\hat{X}_{2} } \right)}$$
(11)

GCN encoder

In this study, we use an encoder integrated with a GCN to extract node embeddings from different views. Specifically, the process replaces the linear layers in the encoder with graph convolutional layers.

$$\:\begin{array}{c}{H}^{\left(l+1\right)}\sigma\:=\left({\stackrel{\sim}{D}}^{-\frac{1}{2}}\stackrel{\sim}{A}{\stackrel{\sim}{D}}^{-\frac{1}{2}}{H}^{\left(l\right)}{W}^{\left(l\right)}\right)\end{array}$$
(12)

This study uses the encoder to fully consider the effective information in the adjacency matrix of the heterogeneous graph MLD and the feature matrix X and to extract low-dimensional embedding vectors. We input the original heterogeneous graph MLD, the augmented heterogeneous graph MLD-A, and the corrupted heterogeneous graph MLD-C into a dual encoder with GCN layers to obtain three low-dimensional embedding vectors: \(\:Z\), \(\:{Z}_{i}\), \(\:{Z}_{j}\).

$$\:\begin{array}{c}Z{=f}_{GCNencoder}\left(MLD,X\right)\end{array}$$
(13)
$$\:\begin{array}{c}{Z}_{i}{=f}_{GCNencoder}\left(MLD-A,{\widehat{X}}_{1}\right)\end{array}$$
(14)
$$\:\begin{array}{c}{Z}_{j}{=f}_{GCNencoder}\left(MLD-C,{\widehat{X}}_{2}\right)\end{array}$$
(15)

Multigraph contrastive learning

We input the three sets of heterogeneous graph views MLD, MLD-A, and MLD-C into the GCN encoder, resulting in three low-dimensional embedding representations: \(\:Z\),\(\:{Z}_{i}\),\(\:{Z}_{j}\). We use a discriminator to perform local graph contrastive learning on \(\:{Z}_{i}\) and \(\:{Z}_{j}\). First, a low-dimensional graph-level embedding representation is generated based on \(\:Z\).

We form a positive sample pair \(\:{z}^{+}\) by combining the graph-level embedding representation with \(\:{\text{Z}}_{i}\), and a negative sample pair \(\:{z}^{-}\) by combining the graph-level embedding representation with \(\:{\text{Z}}_{j}\). The positive and negative sample pairs are then fed into different discriminators for training. Binary cross-entropy is used as the loss function to minimize the loss of positive sample pairs while maximizing the loss of negative sample pairs, ensuring that the low-dimensional embedding \(\:{\text{Z}}_{i}\) can be better distinguished from \(\:{\text{Z}}_{j}\).

Binary Cross-Entropy Loss for Positive Sample Pair:

$$\:\begin{array}{c}{L}_{\text{pos}}=-{\sum\:}_{i}{y}_{i}\cdot\:{log}\left(D\left({z}^{+}\right)\right)+\left(1-{y}_{i}\right)\cdot\:{log}\left(1-D\left({z}^{+}\right)\right)\end{array}$$
(16)

Binary Cross-Entropy Loss for Negative Sample Pair:

$$\:\begin{array}{c}{L}_{\text{neg}}=-{\sum\:}_{i}{y}_{i}\cdot\:{log}\left(D\left({z}^{-}\right)\right)+\left(1-{y}_{i}\right)\cdot\:{log}\left(1-D\left({z}^{-}\right)\right)\end{array}$$
(17)

The final Binary Cross-Entropy Loss:

$$\:\begin{array}{c}{L}_{\text{BCE}}={L}_{\text{pos}}+{L}_{\text{neg}}\end{array}$$
(18)

In addition to local graph contrastive learning, we also implemented global graph contrastive learning. We input the original heterogeneous graph \(\:MLD\:\)and the feature matrix \(\:X\) into the GCN Encoder to obtain the low-dimensional embedding vector \(\:\text{Z}\). We then form a positive sample pair using \(\:\text{Z}\) and \(\:{\text{Z}}_{i}\), and a negative sample pair using \(\:\text{Z}\) and \(\:{\text{Z}}_{j}\). Using cosine similarity, we calculate the similarity of each sample pair, encouraging the model to learn a higher similarity for positive sample pairs and a lower similarity for negative sample pairs.

$$\:\begin{array}{c}{L}_{\text{Contrastive}}=\left(1-{cos}\left(z,{z}_{i}\right)\right)+{max}\left(0,{cos}\left(z,{z}_{j}\right)-m\right)\end{array}$$
(19)

By using both local contrastive learning and global graph contrastive learning, the model can better consider the data’s graph structural information and extract more refined low-dimensional embedding vectors \(\:\:\text{Z}\). The model also enhances its robustness by incorporating noise and variations. The combination of data augmentation, data corruption, and contrastive learning ensures that the model cannot rely on specific details of any given input data during training, thereby preventing overfitting.

$$\:\begin{array}{c}{L}_{\text{total}}={L}_{\text{BCE}}+{L}_{\text{Contrastive}}\end{array}$$
(20)

Results and discussion

This study implements the K-MGCMLD model using Python for the experiments. The hardware environment was as follows: 12th Gen Intel(R) Core(TM) i7-12700 F 2.10 GHz CPU, NVIDIA GeForce RTX 4090 GPU, 16GB RAM, and Windows 10 operating system. K-MGCMLD used a two-layer GCN encoder with an embedding dimension of 256. This study set the learning rate to 0.001 and used Adam as the optimizer.

The Table 3 shows the specific hyperparameter settings:

Table 3 Model hyperparameter settings.
Full size table

This study ran each group 10 times in the clustering experiments, and the average was taken as the experimental result. The prediction experiments used 5-fold cross-validation, with an average of 10 runs taken as the final result. The evaluation metrics used were: The calinski-Harabasz Index (CH Index), Davies-Bouldin Index (DB Index), accuracy, precision, recall, F1-score, and the area under the receiver operating characteristic curve (AUC).

To explore the optimal parameters of the model and demonstrate its effectiveness, we designed the following experiments:

K-means clustering for balancing positive and negative samples

To better balance positive and negative samples and achieve effective prediction results, the value of \(\:k\) was set from 1 to 20 to explore the optimal \(\:k\) value. The CH Index and DB Index were used as clustering evaluation metrics. The formula for the CH Index is as follows:

$$\:\begin{array}{c}CH\:Index=\:\frac{Tr\left({B}_{k}\right)}{Tr\left({W}_{k}\right)}\:\times\:\frac{N-k}{k-1}\end{array}$$
(21)

\(\:\text{T}\text{r}\left({B}_{k}\right)\) is the trace of the between-cluster scatter matrix, which represents the distance between cluster centroids and the global data centroid.

\(\:\text{T}\text{r}\left({W}_{k}\right)\) is the trace of the within-cluster scatter matrix, which represents the distance between each sample point and the cluster centroid.

$$\:\begin{array}{c}{B}_{k}={\sum\:}_{i=1}^{k}{n}_{i}\left({{\upmu\:}}_{i}-{\upmu\:}\right){\left({{\upmu\:}}_{i}-{\upmu\:}\right)}^{T}\end{array}$$
(22)
$$\:\begin{array}{c}{W}_{k}={\sum\:}_{i=1}^{k}{\sum\:}_{x\in\:{C}_{i}}{{n}_{i}\left({{\upmu\:}}_{i}-{\upmu\:}\right)\left({{\upmu\:}}_{i}-{\upmu\:}\right)}^{T}\end{array}$$
(23)

Where \(\:{n}_{i}\) is the number of samples in the i-th cluster, \(\:{\mu\:}_{i}\) is the global centroid of all data points, and \(\:{C}_{i}\) is the set of samples in the \(\:i-\text{t}\text{h}\) cluster. The CH Index measures the ratio of between-cluster cohesion to within-cluster dispersion. A higher CH Index value indicates that the distance between clusters is greater. In contrast, the distance between data points within each cluster is smaller, meaning the data within each cluster is more compact, and the clusters are better separated. Clustering results with larger CH Index values are generally considered more optimal.

The formula for the DB Index is as follows:

$$\:\begin{array}{c}DB\:Index=\:\frac{1}{k}{\sum\:}_{i=1}^{k}\underset{j\ne\:i}{\text{max}}\left(\frac{{s}_{i}+{s}_{j}}{d\left({{\upmu\:}}_{i},{{\upmu\:}}_{j}\right)}\right)\end{array}$$
(24)

\(\:{s}_{i}\) represents the average intra-cluster distance for the \(\:i-th\) cluster, which is defined as:

$$\:\begin{array}{c}{s}_{i}=\frac{1}{{n}_{i}}{\sum\:}_{x\in\:{C}_{i}}\parallel\:x-{{\upmu\:}}_{i}\parallel\:\end{array}$$
(25)

The smaller the DB Index, the better the clustering performance.

To balance positive and negative samples, we conducted experiments on three tasks: miRNA-disease, lncRNA-disease, and lncRNA-miRNA. This study compared clustering results for each task using different k values and visualized the clustering results for the optimal k values.

Table 4; Fig. 2 show the experimental results for miRNA-disease, Table 5; Fig. 3 show the results for lncRNA-disease, and Table 6; Fig. 4 present the visualization of results for lncRNA-miRNA. The specific experimental results are shown in the following tables and figures.

Table 4 Comparison of clustering results for miRNA-disease with different k values.
Full size table
Fig. 2
figure 2

Visualization of clustering results for balancing positive and negative samples in miRNA-Disease.

Full size image
Table 5 Comparison of clustering results for lncRNA-disease with different k values.
Full size table
Fig. 3
figure 3

Visualization of clustering results for balancing positive and negative samples in lncRNA-disease.

Full size image
Table 6 Comparison of clustering results for lncRNA-miRNA with different k values.
Full size table
Fig. 4
figure 4

Visualization of Clustering Results for Balancing Positive and Negative Samples in lncRNA-miRNA.

Full size image

Tables 4, 5, and 6 show the CH Index and DB Index results for clustering negative sample features of miRNA-disease, lncRNA-disease, and lncRNA-miRNA using K-means, respectively. Figures 2-a, 3-a, and 4-a are line charts visualizing the CH Index and DB Index for different k values. Figures 2-b, 3-b, and 4-b present the visualization of negative sample clustering.

From the above line charts, we observed that as k (number of clusters) increases, the CH Index shows a fluctuating upward trend, reaching a peak at k = 5 and gradually decreasing. This indicates that as the number of clusters increases, the between-cluster separation and within-cluster compactness gradually deteriorate, implying a decline in clustering quality. The DB Index generally decreases first and then increases, indicating that the cluster separation initially improves as k increases. However, after k = 5, the DB Index slowly rises, suggesting that cluster overlap increases, reducing clustering quality.

In conclusion, at k = 5, the separation between clusters is optimal, and the compactness of samples within clusters is also the best, resulting in the best clustering performance for the three features. Therefore, this study chooses k = 5 as the number of clusters to balance positive and negative samples.

Comparison of results for different dimensions of embedding vectors

To explore the impact of different embedding dimensions on the prediction results of the K-MGCMLD model, this section conducts comparative experiments for miRNA-disease association prediction, lncRNA-disease association prediction, and lncRNA-miRNA interaction prediction, using embedding dimensions of 32, 64, 128, 256, and 512.

Table 7; Fig. 5 shows the experimental results for miRNA-disease association prediction, Table 8; Fig. 6 present the experimental results for lncRNA-disease association prediction, and Table 9; Fig. 7 display the visualization of results for lncRNA-miRNA interaction prediction. The specific experimental results are shown in the tables and figures below.

Table 7 Comparison of results for different dimensions of embedding vectors in miRNA-disease prediction.
Full size table
Fig. 5
figure 5

Comparison of results for different dimensions of embedding vectors in miRNA-disease prediction.

Full size image
Table 8 Comparison of results for different dimensions of embedding vectors in miRNA-disease prediction.
Full size table
Fig. 6
figure 6

Comparison of results for different dimensions of embedding vectors in lncRNA-disease prediction.

Full size image
Table 9 Comparison of results for different dimensions of embedding vectors in lncRNA-miRNA prediction.
Full size table
Fig. 7
figure 7

Comparison of results for different dimensions of embedding vectors in lncRNA-miRNA prediction.

Full size image

Tables 7, 8 and 9 present the comparison of results for different embedding dimensions for the MDA (miRNA-Disease Association), LDA (lncRNA-Disease Association), and LMI (lncRNA-miRNA Interaction) tasks, respectively, using accuracy, precision, recall, F1-score, and AUC as evaluation metrics. Figures 5-a, 6-a, and 7-a show the ROC curves for different embedding dimensions for each task, while Figs. 5-b, 6-b, and 7-b illustrate the PR curves for different embedding dimensions.

In miRNA-disease association prediction, we found that as the embedding dimension increased, all metrics except precision initially increased and then decreased, with the peak occurring at 256 dimensions, where the AUC reached 0.9542. The improvement in precision gradually diminished, with its values increasing as the dimensionality increased, but the improvement eventually plateaued. For lncRNA-disease association prediction, we observed that, as the embedding dimension increased, most major performance metrics initially increased and then decreased (except recall), peaking at 256 dimensions, where the AUC reached 0.9603. The improvement in recall gradually diminished, increasing with the dimensionality, but the effect eventually plateaued as well. In lncRNA-miRNA interaction prediction, all metrics showed an initial increase followed by a decrease, with the embedding dimension reaching its peak at 256 and the AUC values achieving 0.9687.

In summary, we chose 256 as the dimensionality for the embedding vectors extracted by the model.

Comparison of results for different classifiers

This section compared six classifiers: Decision Tree, Logistic Regression, MLP, SVM, Adaboost, and XGBoost. This study compared miRNA-disease association, lncRNA-disease association, and lncRNA-miRNA interaction predictions. Each experiment used 5-fold cross-validation, with the final average taken as the experimental result.

Table 10; Fig. 8 shows the experimental results for miRNA-disease association prediction, Table 11; Fig. 9 present the experimental results for lncRNA-disease association prediction, and Table 12; Fig. 10 display the visualization of results for lncRNA-miRNA interaction prediction. The specific experimental results are shown in the tables below.

Table 10 Comparison of results for different classifiers in miRNA-disease prediction.
Full size table
Fig. 8
figure 8

Comparison of results for different classifiers in miRNA-disease prediction.

Full size image
Table 11 Comparison of results for different classifiers in lncRNA-disease prediction.
Full size table
Fig. 9
figure 9

Comparison of results for different classifiers in lncRNA-disease prediction.

Full size image
Table 12 Comparison of results for different classifiers in lncRNA-miRNA prediction.
Full size table
Fig. 10
figure 10

Comparison of results for different classifiers in lncRNA-miRNA prediction.

Full size image

In the three prediction tasks (MDA, LDA, and LMI), Tables 10, 11 and 12 show the accuracy, precision, recall, F1-score, and AUC results using six classifiers. Figures 8-a, 9-a, and 10-a show the ROC curves for the different classifiers for each task, while Figs. 8-b, 9-b, and 10-b illustrate the PR curves for the different classifiers.

In these three experiments, we found that the XGBoost classifier achieved the best performance across all five evaluation metrics: accuracy, precision, recall, F1-score, and AUC. XGBoost performed the best among the six classifiers.

XGBoost succeeds due to its robust handling of complex datasets, effective regularization strategy, efficient computational performance, and strong ability to model nonlinear feature interactions. These advantages allow it to perform better than other commonly used classification models across various tasks.

Comparison of experimental results for different models

To demonstrate the superior performance of K-MGCMLD, we compared it with 12 other models in the MDA and LDA association prediction tasks. The comparison included four models for MDA prediction tasks: AGAEMD32, GAEMDA45, SMALF28, and GCLMTP43; four models for LDA prediction tasks: GANLDA37, LDAEXC46, VGAELDA47, and GCLMTP; and four models for LMI prediction tasks: GCLMI48, GCNGRF49, LDAEXC, and GCLMTP. This study used 5-fold cross-validation for each experiment and took the final result as the average of 10 runs. The specific experimental results are presented in the following tables and figures:

Table 13 Comparison of results for different models in miRNA-disease association prediction.
Full size table
Table 14 Comparison of results for different models in lncRNA-disease association prediction.
Full size table
Table 15 Comparison of results for different models in lncRNA- miRNA association prediction.
Full size table
Table 16 Paired t-test between performance and competitive methods of K-MGCMLD.
Full size table
Fig. 11
figure 11

Comparison of results for different models.

Full size image

Tables 13, 14 and 15 compare the experimental results of K-MGCMLD with 12 other advanced models across three different prediction tasks. The results show that, in the MDA prediction task, K-MGCMLD achieved an accuracy of 0.8858, precision of 0.8655, recall of 0.9137, F1-score of 0.8889, and AUC of 0.9542. In the LDA prediction task, K-MGCMLD achieved an accuracy of 0.8917, precision of 0.8786, recall of 0.9092, F1-score of 0.8936, and AUC of 0.9603. In the LMI prediction task, K-MGCMLD achieved an accuracy of 0.9286, precision of 0.9198, recall of 0.9391, F1-score of 0.9294, and AUC of 0.9687. In both the MDA and LDA prediction tasks, K-MGCMLD achieved the highest values across all five evaluation metrics, while in the LMI prediction task, K-MGCMLD achieved the highest values for all metrics except recall. This demonstrates that K-MGCMLD can predict miRNA-disease associations, lncRNA-disease associations, and lncRNA-miRNA interactions.

As shown in Table 16, we conducted paired t-tests on the performance indicators of the model, and the results showed that K-MGCMLD was significantly better than other competitive models.

In addition, to visually compare K-MGCMLD with other models, we also created a radar chart, as shown in Fig. 11.

Case analysis

To further validate the ability of the model to predict associations between noncoding RNAs and diseases, we used the K-MGCMLD model to predict miRNAs related to lung cancer and Alzheimer’s disease, as well as lncRNAs about lung cancer and gastric cancer. We input all candidates and features into the model, which ranked them from highest to lowest score, extracting the top 30 miRNAs and top 20 lncRNAs, respectively. We used the new RNADisease V4.0 database, published in 2023, to verify the miRNA-disease association predictions of the model. Upon validation, this study confirmed all top 30 miRNAs associated with lung cancer and all top 30 miRNAs associated with Alzheimer’s disease. Tables 17, 18, 19 and 20 showed the results.

We used the lnc2cancer v3.0 database (published in 2021) and the RNADisease V4.0 database to verify the lncRNA-disease association predictions. This study validated 18 of the top 20 lncRNAs predicted to be associated with lung cancer. Similarly, 18 of the top 20 lncRNAs predicted to be associated with gastric cancer were validated using databases. Notably, this study did not verify MIR17HG in the database. However, we found evidence linking MIR17HG to gastric cancer in the article “Analysis of the relationship between MIR155HG variants and gastric cancer susceptibility.”

Table 17 Top 30 miRNAs predicted by the model to be associated with lung cancer.
Full size table
Table 18 Top 30 miRNAs predicted by the model to be associated with Alzheimer’s disease.
Full size table
Table 19 Top 20 lncRNAs predicted by the model to be associated with lung cancer.
Full size table
Table 20 Top 20 lncRNAs predicted by the model to be associated with gastric cancer.
Full size table

Conclusion

miRNAs and lncRNAs are two important types of noncoding RNAs. Although they do not encode proteins, they play crucial regulatory roles in the human body. When noncoding RNAs become dysregulated, they can lead to the onset of a wide range of diseases. Therefore, exploring the associations between noncoding RNAs and diseases is paramount. Currently, researchers have proposed various models to predict miRNA-disease and lncRNA-disease associations. However, several significant issues remain unresolved. First, accuracy remains insufficient, making it difficult to accurately predict associations between noncoding RNAs and diseases. Second, although miRNAs and lncRNAs are closely associated with diseases, most experimental methods fail to fully integrate, extract, and utilize the information among miRNAs, lncRNAs, and diseases. Third, most existing models treat miRNA-disease and lncRNA-disease associations separately, making it impossible to predict multiple associations simultaneously.

This study proposes a self-supervised learning framework called K-MGCMLD to address these critical issues. This study effectively integrates information among miRNAs, lncRNAs, and diseases using a model that combines multigraph contrastive learning with GCNs. The K-MGCMLD model consists of four main steps. The first step is the construction of the heterogeneous graph. We integrate correlation and self-correlation information among miRNAs, lncRNAs, and diseases to construct a heterogeneous graph. The model then subjects the graph to data augmentation and corruption. The second step involves downsampling using the K-means clustering algorithm to balance positive and negative samples, allowing the model to learn more effectively. The third step is to use an encoder with a GCN architecture to extract embedding vectors. Multigraph contrastive learning, including both local and global graph contrastive learning, is used to help the embedding vectors better capture the latent topological features of the graph. In the fourth step, this study reconstructs features using the balanced positive and negative samples and the embedding vectors, then feeds them into an XGBoost classifier for multi-association classification prediction.

Through extensive experiments, we demonstrated that K-MGCMLD can achieve high-precision multi-association predictions for miRNA-disease, lncRNA-disease, and lncRNA-miRNA associations. K-MGCMLD outperformed 12 other advanced MDA, LDA, and LMI algorithms. Furthermore, the top 30 miRNAs predicted to be associated with lung cancer and Alzheimer’s disease were all successfully validated, demonstrating the excellent performance of K-MGCMLD. There are still some areas where K-MGCMLD can be improved to make the model more powerful. In the future, we will focus on researching multi-source data and imbalanced datasets. We will integrate more biological data to validate the performance of the model on more rigorous datasets.