Computational analysis of a mathematical model of hookworm infection

Hematophagous nematode parasites known as hookworms have infected over between 576 and 740 million people globally. Since anthelmintic medications are not very effective at preventing reactivation, preventive vaccines are highly sought after. Since whole parasite vaccines are insecure and intolerant, research into substitute subunit vaccines seemed appropriate¹. Hamidu et al. 2024, demonstrated the beneficial effects of a second intervention per year in keeping hookworm infection prevalences low and lowering them even more². Walker et al. 2023, constructed a unique A. ceylanicum multi-host (human and dog) transmission model and evaluated the efficacy of human-only and “One Health” (human plus dog) MDA techniques under various eco-epidemiological hypotheses³. Puchner et al. 2023, examined the unique tool’s further benefit in addition to the vaccine’s biology and implementation viability⁴. Trinos et al. 2023, investigated the costs and benefits of mass medicine delivery in Dak Lak province, Vietnam, in comparison to school-based targeted preventative chemotherapy for the treatment of hookworms⁵. Santos et al. 2023, investigation verified a statistically significant drop in the prevalence of hookworm infection between the two time periods studied⁶. Ramlal et al. 2023, provided a general overview of the potential use of plant-based compounds, or botanicals, made from a variety of medicinal herbs to treat important parasites that cause the condition, systemic hookworm infections that cause the disease and infections, and ultimately death in humans. In contrast, conventional treatments are much less effective and have a great deal of adverse consequences⁷. Tiremo et al. 2023, analyzed that the diagnosis of unexpected parasitic infections, such as hookworms, can be made with a meticulous endoscopic examination of the small intestine mucosa in patients with IDA who have experienced gastrointestinal bleeding⁸. Mustapha et al. 2020, established and evaluated an analytical representation of the dynamics of hookworm propagation involving two independent infection categories and stages of parasite development⁹. Qureshi et al. 2020, constructed and investigated a model utilizing the Caputo fractional order differential operator to simulate the dynamics of Hookworm passing on infection in a human individual¹⁰. Sangari et al. 2020, provided an analytical study and modeling of the fluctuations of hookworm transmission in the Obi Local Government Area of Nasarawa State, Nigeria. In an attempt to control the disease, a numerical model of hookworm transmission was created¹¹. Malizia et al. 2024, created a structure-based statistical approach that took into consideration low hemoglobin levels resulting from different sources to simulate individual hemoglobin concentrations in hookworm infections¹². Ajjampur et al. 2021, observed that it is necessary for a community-based strategy to address the high prevalence of hookworm in adults in the present scenario¹³. Grolimund et al. 2022, recognized the uncertainty of the suggested Kato-Katz thick smear diagnostic procedure, a Bayesian model was created to compare the “true” CR and egg reduction rate of various treatment regimens for infections with hookworms¹⁴. Clements et al. 2022, conducted two comprehensive evaluations of research on the distribution of hookworms separated by species and genus across different parts of the globe, as well as the relationships between infections caused by hookworm species and clinical results, especially severe anemia¹⁵. Haldeman et al. 2020, analyzed that mostly affecting the world’s impoverished communities, human hookworm is an essential cause of mortality worldwide and is a soil-transmitted helminth (STH) ailment triggered by either Nectar americanus duodenale¹⁶. İlhan et al. 2022, utilized the fractional derivative and integral operator proposed by Caputo and Fabrizio, and the Hookworm infection model is analyzed¹⁷. Koopman et al. 2021, operated human infections with Schistosoma and hookworm are an important tool in the production of vaccines¹⁸. Colella et al. 2021, determined and compared, particularly to a species remission and egg diminution incidences of single-dose albendazole (400 mg) versus hookworm infections at the household level employing standard fecal flotation (SFF) and a multiplex qPCR technique¹⁹. The authors studied backward bifurcation and control in transmission dynamics of arboviral diseases in²⁰. The authors made a comparative study of machine learning and deep learning methods for flood forecasting in the Far-North region, Cameroon, and fractional dynamics of a Chikungunya transmission model in^21,22 respectively. The authors studied projections and fractional dynamics of typhoid fever: a case study of Mbandjock in the Centre Region of Cameroon²³. Chazuka et al. studied strategic approaches to mitigating Hookworm infection: an optimal control and cost-effectiveness analysis in²⁴.

Stochastic analysis in epidemiology incorporates randomness into models to correctly replicate disease spread while accounting for human behavior variations and environmental influences. This approach improves prediction accuracy and informs disease management efforts.

• A stochastic delay model for the propagation of diseases is deduced from epidemiological assumptions.

• The reproductive number, and equilibria of the deterministic systems are calculated.

• Feasible Properties of the model are studied rigorously.

• An NSFD scheme to solve the stochastic delay system is proposed and theoretically analyzed.

• The simulations show that the scheme is epidemiologically more robust than other approaches.

The paper is structured as follows: A brief analysis of hookworm infections Sect. 1 provides a thorough overview of the literature. Section 2 focuses on developing the delayed model and doing the subsequent mathematical analysis. In addition, reproduction numbers and equilibria are investigated. Sections 3 and 4 describe the stochastic conceptualization processes. The numerical approach to the NSFD technique is provided in Sect. 5. Section 6 focuses explicitly on numerical simulations and the presentation of results. The final opinions provide a comprehensive summary of the work in Sect. 7.

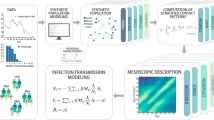
The model is based on monitoring the dynamics of hookworm and human populations at any time t of \(\:S\left(t\right)\) susceptible humans, \(\:E\left(t\right)\) exposed humans, \(\:{I}_{1}\left(t\right)\) infectious humans, \(\:{I}_{2}\left(t\right)\) infectious humans with heavy infection, \(\:R\left(t\right)\) humans recovered and \(\:F\left(t\right)\) worm eggs, \(\:{L}_{1}\left(t\right)\) non-infective larvae, and \(\:{L}_{2}\left(t\right)\) infectious larvae. (See Fig. 1)¹⁰.

Flowchart of hookworm infection with time delay.

Full size image

The human population is being recruited at a rate of \(\:\pi\:\) (by migration or birth) and a rate of \(\:\gamma\:\) due to the progression of persons from the recovery class. When susceptible individuals \(\:S\left(t\right)\) come into touch with infectious larvae, they become infected at a rate of \(\:\lambda\:S\left(t\right){L}_{2}\left(t\right)\). \(\:S\left(t\right)\) does not instantly become infected upon infection instead it enters an exposed class. Individuals who are exposed to infection proceed to the infectious class of either heavy infection or moderate infection at a rate of, respectively, \(\:\left(1-\epsilon\:\right)\sigma\:\) and \(\:\epsilon\:\sigma\:\). An individual with moderate infectiousness advances at a pace of \(\:{\tau\:}_{1}\) to acquire heavy illnesses. Recovery from a moderate infection occurs at a pace of \(\:{\theta\:}_{1}\) (awareness and improvement of personal cleanliness), whereas chemotherapy treatment causes a heavy infection to recover at a rate of \(\:{\theta\:}_{2}\). Eggs in feces are excreted at rates of \(\:\alpha\:\) by moderately and heavily infected people, and after \(\:\omega\:\) days, the eggs hatched to become \(\:{L}_{1}\left(t\right)\) and \(\:{L}_{2}\left(t\right)\), respectively. \(\:\mu\:\) and \(\:\delta\:\) represent the natural death rate of humans and the disease-induced mortality rate, respectively, whereas \(\:\varphi\:\), \(\:v\), and \(\:k\) represent the death rates for eggs, non-infective larvae, and infectious larvae. Also, \(\:\tau\:\) is delay parameter for this particular model. Hookworm transmission dynamics in human populations are described by the following differential equations with artificial delay parameter \(\:{e}^{-\mu\:\tau\:}\) as follows:

with initial conditions; \(\:S\left(0\right)\ge\:0,\:E\left(0\right)\ge\:0,\:{I}_{1}\left(0\right)\ge\:0,\:{I}_{2}\left(0\right)\ge\:0,\:R\left(0\right)\ge\:0,\)\(\:F\left(0\right)\ge\:0,\:{L}_{1}\left(0\right)\ge\:0,\:{L}_{2}\left(0\right)\ge\:0\) for all \(\:t\ge\:0,\:\tau\:<t\).

Model properties

In this section, we discussed the positivity and boundedness of solutions of system (1) with initial conditions.

For positivity and boundedness, we used the following results.

Theorem 1

For any \(t\ge 0\), the solutions of system (1) with initial conditions are positive.

Proof

The following can be determined from the system (1):

as desired.

Theorem 2

Solutions of the system (1) with initial condition are bounded.

Proof

Let’s examine the function in this particular way:

For detailed proof see appendix A.

Model equilibria

In this section, we evaluate two different types of equilibria for the system (1), as follows:

Hookworm-free equilibrium (HFE), \(\:{\mathcal{H}}^{0}=\left({S}^{0},{E}^{0},\:{I}_{1}^{0},\:{I}_{2}^{0},{R}^{0},{F}^{0}\:{L}_{1}^{0},\:{L}_{2}^{0}\right)=\left(\frac{\pi\:}{\mu\:},\text{0,0},\text{0,0},\text{0,0},0\right)\) and Hookworm endemic equilibrium (HEE), \(\:{\mathcal{H}}^{*}=\left({S}^{*},{E}^{*},\:{I}_{1}^{*},\:{I}_{2}^{*},{R}^{*},{F}^{*},\:{L}_{1}^{*},\:{L}_{2}^{*}\right)\) where

where \(\:{A}_{1}=\sigma\:+\mu\:\), \(\:{A}_{2}=\left({\tau\:}_{1}+\mu\:+{\theta\:}_{1}\right)\), \(\:{A}_{3}=\left(\delta\:+\mu\:+{\theta\:}_{2}\right)\), \(\:{A}_{4}=\left(\psi\:+\omega\:\right)\), \(\:{A}_{5}=\left(v+\varphi\:\right)\), \(\:Q=\left(1-\epsilon\:\right)\sigma\:\).

Reproduction number is of vital importance for epidemiology as a critical threshold that potentially influences the spread of disease. It is the mean number of secondary infections transmitted by an infected person in a fully susceptible population. In the context of the Hookworm model, we estimate this threshold to understand and predict the infection behavior in the population. The reproduction number for the model system (1) is computed using a systematic methodology that is founded upon the next-generation matrix method as described in²⁴. The transmission matrix (F) and transition matrix (G) are derived by substituting the Hookworm-free equilibrium and taking into account the affected classes from the system (1). The largest eigenvalue of \(\:F{G}^{-1}\) represents the reproduction number.

Therefore, Reproduction number is;

Let us consider the vector \(\:A={\left[S\left(t\right),\:E\left(t\right),{I}_{1}\left(t\right),{I}_{2}\left(t\right),R\left(t\right),F\left(t\right),{L}_{1}\left(t\right),{L}_{2}\left(t\right)\right]}^{T}\) and the number of chances of an event is presented in Table 1. For the drift and diffusion coefficients of the system (1), we shall calculate the expectation and variance as follows:

Therefore,

The Eq. (4), is called the stochastic delay differential equation with \(\:B\left(t\right)\) is the Brownian.

In this section, we use a conventional numerical technique for approximating a stochastic delayed model’s result of (4). In this regard, we admitted \(\:{I}_{q}=\{\text{0,1},\text{2,3},\dots\:,q\}\) for each q ∈ \(\:\mathbb{N}\). Let \(\:N\in\:\mathbb{N}\), and with the effect of time ∆t divides the partition into equal intervals [0, T] with constant delay as

for each n ∈ \(\:{I}_{N}\). Needless to mention \(\:{t}_{n}={\uptau\:}_\text{n}\), for each n ∈ \(\:{I}_{N}\). Moreover, we agreed that \(\:{U}^{n}=U\left({t}_{n}\right)\), whenever n ∈ \(\:{I}_{N}\) and U = \(\:S,\:E,{I}_{1},{I}_{2},R,F,{L}_{1},{L}_{2}\). Also, we set

∆\(\:{B}_{n}\) = B (\(\:{t}_{n+1}\)) − B (\(\:{t}_{n}\)), ∀n ∈ \(\:{I}_{N-1}\). The mean of each ∆\(\:{B}_{n}\) follows a normal distribution with a variance of one and an average of zero.

The Euler-Maruyama technique to simulate the outcomes of Eq. (4) as follows:

Where the value of \(\:\varDelta\:t\) indicates the discretization parameter.

The system of stochastic delay differential equations (SDDEs) is a mathematical model that describes the evolution of a set of variables over time, where the equations involve both deterministic time delays and stochastic (random) components. Where the stochastic term \(\:{\sigma\:}_{i}:\left(i=1,\:2,\:3,\:\text{4,5},\text{6,7},8\right),\:\left(B\left(t\right)\right)\) introduces randomness into the system of differential equations as follows:

where \(\:B\left(t\right)\) participation in the Brownian motion and the unpredictability of each compartment are indicated by \(\:{\sigma\:}_{i};i=\text{1,2},\text{3,4},\text{5,6},\text{7,8}\). Also, the initial conditions of the model (6) as follow: \(\:S\left(0\right)\ge\:0,E\left(0\right)\ge\:0,{I}_{1}\left(0\right)\ge\:0,{I}_{2}\left(0\right)\ge\:0,R\left(0\right)\ge\:0,F\left(0\right)\ge\:0,{L}_{1}\left(0\right)\ge\:0,{L}_{2}\left(0\right)\ge\:0\).

For positivity and boundedness of system (6), we assume the following vector, let’s

and norm

Moreover, let \(\:{D}_{1}^{\text{7,1}}\left({\mathbb{R}}^{8}x\left(0,\infty\:\right):{\mathbb{R}}_{+}\right)\) represents the set of all positive functions \(\:{U}_{1}\left(V,t\right)\) that are subsequently defined on \(\:{\mathbb{R}}^{8}x\left(0,\infty\:\right)\). Furthermore, in V the function is once differentiable and twice differentiable. The differentiable operator \(\:{T}_{1}\), associated with eight-dimensional stochastic delay differential equations (SDDEs), has been developed.

As,

If \(\:{T}_{1}\) acts on function \(\:{V}^{*}\in\:{D}_{1}^{\text{7,1}}\left({\mathbb{R}}^{8}x\left(0,\infty\:\right):{\mathbb{R}}_{+}\right)\) then we denote

Where Transportation is represented by T.

Theorem 3

For model (6) and any given initial value \((S(0), E(0),I_{1}(0),I_{2}(0),R(0),F(0),L_{1}(0), L_{2}(0)) \in\:{\mathbb{R}}_{+}^{8}\), there is a unique solution \((S(t), E(t),I_{1}(t),I_{2}(t),R(t),F(t),L_{1}(t), L_{2}(t)) \in\:{\mathbb{R}}_{+}^{8}\) and will remain in \({\mathbb{R}}_{+}^{8}\) with probability one.

Proof

Considering that every model parameter meets the local Lipschitz constraints. Consequently, the above model has a positive solution locally on the interval \([0,\:\tau_e\:]\)according to Ito’s formula, where \(\tau_e\) represents the explosion time. When \(\tau_e\) equals infinity, it may be demonstrated that the model has a global solution.

If \(\:{n}_{0}=\:0\), then a sufficiently large number is required such that \(\:S\left(0\right),E\left(0\right),{I}_{1}\left(0\right),{I}_{2}\left(0\right)R\left(0\right),F\left(0\right),\)\(\:{L}_{1}\left(0\right),{L}_{2}\left(0\right)\) fall inside the interval \(\:\left\{\frac{1}{{n}_{0}},{n}_{0}\right\}\).

For each positive integer \(\:n\), let’s define a series in the following manner:

Here, \(\:\phi\:\) is the empty set, and we set \(\:inf\phi\:\) =\(\:\infty\:\). Since \(\:n\) approaches \(\:\infty\:\) without reducing \(\:{\tau\:}_{n}\),

According to the inequality, \(\:{\tau\:}_{\infty\:}\) is either equal to or smaller than \(\:{\tau\:}_{e}\).

Our goal now is to show that, as we expected, \(\:{\tau\:}_{\infty\:}\) equals infinity.

If this condition fails to be satisfied, then there exist values T > 0 and \(\:{b}_{1}\in\:\:(0,\:1)\) that satisfy the statement.

By using Ito’s formula, we calculate

To simplify, we assume \(\:{M}_{1}=(\pi\:+5\mu\:+\sigma\:+{\tau\:}_{1}+{\theta\:}_{1}+\delta\:+{\theta\:}_{2}+\gamma\:+\psi\:+\omega\:+v+\varphi\)\(\:+k+\frac{{\sigma\:}_{1}^{2}+{\sigma\:}_{2}^{2}+{\sigma\:}_{3}^{2}+{\sigma\:}_{4}^{2}+{\sigma\:}_{5}^{2}+{\sigma\:}_{6}^{2}+{\sigma\:}_{7}^{2}+{\sigma\:}_{8}^{2}}{2})\)

Then Eq. (13) could be written as:

Following the integration from 0 to \(\:{\tau\:}_{n}\wedge\:\tau\:\), where \(\:{M}_{1}\) is a positive constant,

We obtain,

When \(\:{\tau\:}_{n}\wedge\:\tau\:=\text{min}\left({\tau\:}_{n},T\right)\), applying the assumptions results in

Set \(\:{{\Omega\:}}_{n}=\{{\tau\:}_{n}\le\:T\}\) for \(\:n>{n}_{1}\) and from (11), we have \(\:X\left({{\Omega\:}}_{n}\ge\:b\right).\:\)

There are certain indices such that \(\:{V}_{i}\left({\tau\:}_{n},{a}_{1}\right)=n\) or \(\:\frac{1}{n}\) for each member \(\:{a}_{1}\) in the collection \(\:{{\Omega\:}}_{n}\), where has the values 1, 2, 3,4,5,6,7, and 8.

Hence, \(\:{V}^{*}(\left(S\left({\tau\:}_{n},{a}_{1}\right),E\left({\tau\:}_{n},{a}_{1}\right),{I}_{1}\left({\tau\:}_{n},{a}_{1}\right),{I}_{2}\left({\tau\:}_{n},{a}_{1}\right)\right.,\) \(R\left({\tau\:}_{n},{a}_{1}\right),F\left({\tau\:}_{n},{a}_{1}\right),\)\(\left. \left.{L}_{1}\left({\tau\:}_{n},{a}_{1}\right),{L}_{2}\left({\tau\:}_{n},{a}_{1}\right),\right)\right)\) is less than \(\:\text{min}\left\{n-1-\text{ln}n,\frac{1}{n}-1-\text{ln}\frac{1}{n}\right\}\)

Next, we obtain

Within the set \(\:{{\Omega\:}}_{n}\), the indicator function is represented by the notation \(\:{I}_{{{\Omega\:}}_{n}\left({a}_{1}\right)}\).

The contradiction arises when n gets closer to infinity: infinity is equivalent to \(\:{V}^{*}\left(S\left(0\right),E\left(0\right),{I}_{1}\left(0\right),{I}_{2}\left(0\right),R\left(0\right),F\left(0\right),{L}_{1}\left(0\right),{L}_{2}\left(0\right)\right)+{M}_{1}T\), which has a finite value. as desired.

Assume that \(\:{\mathcal{U}}_{n}\) is the set that \(\:{\mathcal{U}}_{e}=\left\{\text{0,1},2\dots\:,\it{e}\right\}\) defines for every \(e\,\epsilon\:\mathbb{N}\). In this part, we will identify and examine the system’s discretization (6). To accomplish our goal, we take into account the temporal interval when \(\:T>0\). Make a consistent division of the time interval [0, T] into n subintervals, each having a length of \(\:k=\frac{T}{e}\). With \(\:{t}_{a}=ak\), for every \(a\:\epsilon{I}_e\), where \(I_e\) is the set of indices. The functions \(\:{S}^{m},{E}^{m},{I}_{1}^{m},\:{I}_{2}^{m},{R}^{m},{F}^{m},\:{L}_{1}^{m}\) and \(\:{L}_{2}^{m}\) correspond to the numerical approximations for S, E, \(\:{I}_{1}\), \(\:{I}_{2}\), R, F, \(\:{L}_{1}\) and \(\:{L}_{2}\). \(\:\left({S}^{0},{E}^{0},\:{I}_{1}^{0},\:{I}_{2}^{0},{R}^{0},{F}^{0}\:{L}_{1}^{0},\:{L}_{2}^{0}\right)\) are the discrete starting data. It is defined so that \(\:{S}^{0}=S\left(0\right),{E}^{0}=E\left(0\right),\:{I}_{1}^{0}={I}_{1}\left(0\right),{I}_{2}^{0}={I}_{2}\left(0\right),\:{R}^{0}=R\left(0\right),{F}^{0}=F\left(0\right),\:{L}_{1}^{0}={L}_{1}\left(0\right),\:{L}_{2}^{0}={L}_{2}\left(0\right)\) as required.

Stochastic nonstandard computational method

A stochastic non-standard finite difference methodology might be used to solve model (6) in our parametric perturbation model. The susceptible class from the model (6) can be expressed using an unusual computing method.

The equation for the stochastic NSFD technique looks like this:

The stochastic NSFD process, as demonstrated in (18), may be used to decompose the system (6), and the resultant whole system can be expressed as follows:

Here, \(\:n=\text{0,1},2,\dots\:\) and \(\:\varDelta\:{\text{B}}_{n}=\varDelta\:{\text{B}}_{{t}_{n+1}}-\varDelta\:{\text{B}}_{{t}_{n}}\) represents a generic normal distribution that is, \(\:\varDelta\:{\text{B}}_{\text{n}}\sim\text{N}(0,\:1\)).

Convergence analysis of nonstandard computational method

The following theorems are stated concerning the convergence analysis.

Theorem 4

For all initially values of \((S(0), E(0),I_{1}(0),I_{2}(0),R(0),F(0),L_{1}(0), L_{2}(0)) \in\:{\mathbb{R}}_{+}^{8}\), there is only one positive solution \((S(t), E(t),I_{1}(t),I_{2}(t),R(t),F(t),L_{1}(t), L_{2}(t)) \in\:{\mathbb{R}}_{+}^{8}\:\forall\:n > 0\).

Proof

The proof is easily demonstrable, due to the non-negative nature of the biological problems’ restriction.

Theorem 5

For the \({\cal{G}}=(S^n,E^n,I_1^n,I_2^n,R^n,F^n,L_1^n,L_2^n ) \in \mathbb{R}_+^8\)\(:S^n+E^n+I_1^n+I_2^n+R^n+F^n+L_1^n+L_2^n\) \(=N \leq \frac{\pi}{\mu}, S^n \geq 0,E^n\geq 0,I_1^n\geq 0,I_2^n\geq 0,R^n\geq 0,\)\(F^n\geq 0,L_1^n\geq 0,L_2^n\geq 0,\) region. For every \(n \ge 0\), is an area of equations that is feasible and positive invariant (34) to (41).

Proof

The deconstruction of the system (19) looks like this:

Once the aforementioned equation system is included, we obtain

Therefore, for any \(\:n>0\), the non-standard computing approach that we suggest is restricted.

Theorem 6

If the unit circle contains the eigenvalue, the computational approach that has been given is stable for any \(\:n>0\) with \(\triangle\:B_{n} = 0.\)

Proof

Assume that the functions A, B, C, D, F, G, H, and P correspond to the right-hand sides of the following equations: (19).

Here,

\(\:A=\frac{S+h\left[\pi\:+\gamma\:R\right]}{1+h\left(\lambda\:{L}_{2}{e}^{-\mu\:\tau\:}+\mu\:\right)}\), \(\:B=\frac{E+h\left[\lambda\:S{L}_{2}{e}^{-\mu\:\tau\:}\right]}{1+h\left(\mu\:+\epsilon\:\sigma\:+\left(1-\epsilon\:\right)\sigma\:\right)}\) ,\(\:C=\frac{{I}_{1}+h\left[\left(1-\epsilon\:\right)\sigma\:E\right]}{1+h\left({\tau\:}_{1}+\mu\:+{\theta\:}_{1}\right)}\), \(\:D=\frac{{I}_{2}+h\left[\epsilon\:\sigma\:E\right]}{1+h\left(\delta\:+\mu\:+{\theta\:}_{2}\right)}\) ,

It is commonly understood that a system of the forms (6) converges to the model’s optimal state if and only if the Jacobian’s spectral radius, (J),

For the model’s stability. It complies with the requirements:

The equilibrium of the model is stable for \(\:\rho\:\left(J\right)<1\). Whether \(\:\rho\:\left(J\right)>1\) determines whether the equilibria of the model are stable. The equilibrium states of the model are inherently stable when \(\:\rho\:\left(J\right)=1\).

The following is an expression for the elements of the method-related Jacobian:

Hookworm-free equilibrium (HFE), \(\:{\mathcal{H}}^{0}=\left({S}^{0},{E}^{0},\:{I}_{1}^{0},\:{I}_{2}^{0},{R}^{0},{F}^{0}\:{L}_{1}^{0},\:{L}_{2}^{0}\right)=\left(\frac{\pi\:}{\mu\:},\text{0,0},0,\text{0,0},\text{0,0}\right)\)

Thus, the Jacobian’s eigenvalues at \(\:{\mathcal{H}}^{0}\) are as follows:

\(\:{\lambda\:}_{1}=\frac{1}{1+h\left(\mu\:\right)}<1\), \(\:{\lambda\:}_{3}=\frac{1}{1+h\left({\tau\:}_{1}+\mu\:+{\theta\:}_{1}\right)}\), \(\:{\lambda\:}_{4}=\frac{1}{1+h\left(\delta\:+\mu\:+{\theta\:}_{2}\right)}\), \(\:{\lambda\:}_{5}=\frac{1}{1+h\left(\mu\:+\gamma\:\right)}\), \(\:{\lambda\:}_{6}=\frac{1}{1+h\left(\psi\:+\omega\:\right)}\), \(\:{\lambda\:}_{7}=\frac{1}{1+h\left(v+\varphi\:\right)}\), \(\:{\lambda\:}_{8}=\frac{1}{1+hk}\) provided that \(\:{R}_{0}<1\) and \(\:{\lambda\:}_{2}=\frac{1}{1+h\left(\mu\:+\epsilon\:\sigma\:+\left(1-\epsilon\:\right)\sigma\:\right)}<1\).

Thus, all the eigenvalues lie in the unit circle at hookworms’ free equilibrium point. As desired.

This section contrasts a non-standard computing method with established numerical methodologies (see Table 2).

Analysis of Euler-Maruyama versus stochastic NSFD methods (a) Graphical solution of infected humans with heavy infections at \(\:h=\)0.01 (b) Graphical solution of infected humans with heavy infections at \(\:h=\)1

Full size image

Analysis of stochastic Euler versus stochastic NSFD methods. (a) Graphical solution of infected humans with heavy infections at \(\:h=\)0.1 (b) Graphical solution of infected humans with heavy infections at \(\:h=\)2.

Full size image

Analysis of stochastic Range Kutta versus stochastic NSFD methods. (a) Graphical solution of infected humans with heavy infections at \(\:h=\)0.1 (b) Graphical solution of infected humans with heavy infections at \(\:h=\)3.

Full size image

Comparison of stochastic NSFD method on time-delayed susceptible and infected humans with heavy infections population (a) Impact of susceptible humans for different values of delay parameter (b) Impact of infected humans for different values of delay parameter.

Full size image

Temporal comparison of the reproduction number with incorporated time-delay effects.

Full size image

Discussion

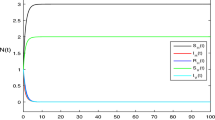
This section provides a discussion of the graphical presentation of the standard and nonstandard methods like Euler Maruyama, stochastic Euler, stochastic Runge Kutta, and nonstandard finite difference (NSFD) methods. Figure 2a,b present a comparative analysis of infected human populations under heavy infection scenarios using the Stochastic Non-Standard Finite Difference (NSFD) method and the Euler-Maruyama method. At a step size of \(\:h=0.01\), both methods exhibited convergence as shown in Fig. 2a. However, when the step size was increased to \(\:h=1\), the Euler-Maruyama method diverged while the Stochastic NSFD method-maintained convergence, as illustrated in Fig. 2b. Figure 3a,b analyze the population of infected humans with heavy infections using the Stochastic NSFD and Stochastic Euler Method. Both methods showed convergence at \(\:h=0.01\) in Fig. 3a. However, when the step size increased to \(\:h=2\) at the hookworm endemic point, the Stochastic Euler Method diverged, whereas the Stochastic NSFD method continued to converge, as depicted in Fig. 3b. Figure 4a,b analyze the population of infected humans under heavy infections using the Stochastic NSFD and Stochastic RK methods. Convergence is observed in both methods at \(\:h=0.01\) in Fig. 4a. However, at the hookworm endemic point, increasing the step size to \(\:h=3\) results in divergence for the Stochastic RK Method, whereas the Stochastic NSFD method maintains convergence, as illustrated in Fig. 4b. In Fig. 5a, the graph illustrates how varying delays \(\:\tau\:=1,\:2,\:3,\:4,\:5\) affect the susceptible class of the model. Figure 5b demonstrates the impact of these delays on the infected class across τ values \(\:1,\:2,\:3,\:4,\:and\:5\), showing a gradual reduction in disease prevalence over time. Figure 6 compares the delay terms \(\:\tau\:\) with the basic reproduction number \(\:{\:R}_{0}\). As \(\:\tau\:\) increases, \(\:{\:R}_{0}\) shows a decreasing trend. Specifically, at \(\:\tau\:=1.80\) days, \(\:{\:R}_{0}\) equals 1.042, indicating a diminishing disease presence in the host population over time.

In this paper, we developed and analyzed a model for the transmission dynamics of Hookworm infection in a human population using stochastic delay differential equations. The feasible properties of the model like positivity and boundedness studied. Also, we discuss two states of the model Hookworm free equilibrium and hookworms endemic equilibrium. Also, the reproduction number of the delayed model is investigated. After that, we studied the stochastic formation of the model in two ways transition probabilities and non-parametric perturbations, and verified the positivity and boundedness of the model. Due to nonlinearity and nondifferentiable terms of Brownian motion, these stochastic systems have no analytical solutions. So, we have used some standard and nonstandard numerical methods for its results. The implementation of standard methods like Euler Maruyama, Stochastic Euler, and stochastic Runge Kutta many discrepancies such as negative and unbounded results for the different values of time size, and did not apprehend a long-term behavior of the disease. To overcome such discrepancies, we used a stochastic nonstandard method for its results which restored the dynamical properties of the model and free of-time step size. Results from our modeling suggest that chemotherapy is administered to individuals infected with Hookworm, awareness campaigns of prevention methods, and well-known personal hygiene procedures including bathing and public toilets.

In future work, we will also seek optimal control strategies to minimize the emergence of moderate and severe infections in our future work. These strategies will also aim to reduce the cost of management within an optimally-designed Hookworm control system.