Abstract
Personalized tourism has recently become an increasingly popular mode of travel. Effective personalized route recommendations must consider numerous complex factors, including the vast historical trajectory of tourism, individual traveler preferences, and real-time environmental conditions. However, the large temporal and spatial spans of trajectory data pose significant challenges to achieving high relevance and accuracy in personalized route recommendation systems. This study addresses these challenges by proposing a personalized tourism route recommendation model, the Temporal Multilayer Sequential Neural Network (TMS-Net). The fixed-length trajectory segmentation method designed in TMS-Net can adaptively adjust the segmentation length of tourist trajectories, effectively addressing the issue of large spatiotemporal spans by integrating tourist behavior characteristics and route complexity. The self-attention mechanism incorporating relative positional information enhances the model’s ability to capture the relationships between different paths within a tourism route by merging position encoding and distance information. Additionally, the multilayer Long Short-Term Memory neural network module, built through hierarchical time series modeling, deeply captures the complex temporal dependencies in travel routes, improving the relevance of the recommendation results and the ability to recognize long-duration travel behaviors. The TMS-Net model was trained on over six million trajectory data points from Chengdu City, Sichuan Province, spanning January 2016 to December 2022. The experimental results indicated that the optimal trajectory segmentation interval ranged from 0.8 to 1.2 h. The model achieved a recommendation accuracy of 88.6% and a Haversine distance error of 1.23, demonstrating its ability to accurately identify tourist points of interest and provide highly relevant recommendations. This study demonstrates the potential of TMS-Net to improve personalized tourism experiences significantly and offers new methodological insights for personalized travel recommendations.
Similar content being viewed by others
Introduction
Personalized tourism is an emerging mode of travel that customizes itineraries based on individual interests and preferences, offering tourists enhanced comfort and satisfaction during their journeys1,2. In recent years, scholarly interest in developing intelligent recommendation technologies for personalized travel routes has grown, aiming to offer more flexible and personalized services and enhance the overall travel experience3,4,5,6. These personalized recommendations consider factors such as timing, ___location, duration of stay, upcoming attractions, and historical points of interest7,8,9,10. Although traditional mathematical models are simple and efficient, they often overlook time-series information, cannot adjust routes dynamically, and fail to capture subtle changes in user preferences and interests11,12,13,14.
Therefore, several researchers have utilized deep learning models in this ___domain15,16. Kulshrestha et al. proposed a Bayesian bidirectional Long Short-Term Memory (LSTM) network to predict tourism demand17. Building on this, Sandfort et al. introduced a generative adversarial network for data augmentation method18, whereas Law et al. applied deep learning to establish the relationship between factors predicting tourism demand and tourist arrivals19. Chen et al. utilized adaptive genetic and seasonal index adjustment algorithms to generate route recommendations for tourists20. For the visual analysis of tourism behavior, Zhang et al. employed visual technology to map and recognize the cognitive perceptions of tourists21. Ma et al. applied this technique and found that combining comment text with user photos was the most effective approach for predicting comment usefulness22. Li et al. developed a dual-channel convolutional neural network-LSTM model to address the challenge of predicting emotional polarity in tourist-generated content23, which Lum et al. later used to process data from multiple sources24. Hu et al. applied the density-based spatial clustering of applications with noise clustering algorithm to identify urban areas of interest and detect spatial-temporal dynamics25, whereas Colladon et al. demonstrated that language complexity and network centralization were significant predictors of visits to scenic spots26. After analyzing the road network, Colak et al. concluded that moderately centralized route optimization can significantly reduce traffic congestion27. Additionally, Wang et al. developed an AI-based Internet of Things system that solves the problem of massive data processing and low-latency communication in intelligent tourism applications28.
Research highlights the importance of deep learning models in improving the accuracy of travel route recommendations. These models excel in processing complex features and providing personalized recommendations. However, challenges remain in terms of managing large temporal spans on prediction accuracy and capturing user preferences with greater agility. To address these challenges, this study proposes a multilayer neural network prediction model called the Temporal Multilayer Sequential Neural Network (TMS-Net). This model incorporates a time-attention mechanism that integrates relative ___location information to maintain correlations between attractions both before and after processing. In addition, it introduces a multilayer LSTM network that incorporates scenic spot characteristics as weighting factors. This approach aims to mitigate the degradation of temporal information over time and accurately analyze the travel intentions of tourists.
Related work
Fixed-length trajectory segmentation method
Tourists spend varying amounts of time at different attractions. Research in time-series segmentation has primarily explored two approaches: “dynamic segmentation” and “fixed segmentation.” Table 1 presents relevant research on trajectory segmentation. Although dynamic segmentation offers flexibility, it can lead to inconsistent inputs, making it difficult for the model to learn stable temporal dependencies, thereby reducing training stability. This study adopts a fixed time interval for segmenting historical tourist trajectory data based on these findings. Using segmented data as input for the TMS-Net model helps address variations in stay durations. Showing a 36% improvement in model training convergence speed compared to dynamic segmentation. This consistent segmentation approach ensures that each time slice contains sufficient data points, enabling effective capture of tourist behavior patterns.
Tourist preferences for delicacy
Personalized tourism services are typically determined by analyzing historical visits of tourists to attractions, incorporating their characteristics and behaviors. Table 2 presents selected studies on extracting tourist preferences. The analysis reveals that incorporating an attention mechanism into the LSTM model results in higher accuracy in interest extraction. This study focuses on user interests by preprocessing, and extracting features such as the types of attractions visited, length of stay, and selected routes through encoding. The model uses an attention mechanism that integrates relative positional information to maintain a complete sequential relationship between tourist visits. It then employs a multilayer memory neural network to capture dynamic patterns and long-term dependencies in tourism data, effectively extracting features of tourist travel intentions. In experimental comparisons with current mainstream models, the TMS-Net model achieves an accuracy of 88% in extracting tourist interests.
Personalized route recommendation framework
Personalized attraction recommendations involve analyzing historical trajectories and preferences of tourists. Table 3 presents relevant research on personalized route recommendation. This study divides historical trajectories into fixed time intervals and constructs a time-series attention framework by integrating relative positional information. Furthermore, it utilizes a multilayer LSTM to train each segmented dataset, preserving associations with past and future timesteps. Finally, a feedforward neural network converts the vectorized information into recommended tourist attractions.The TMS-Net model achieved a Haversine distance error of only 1.23 in attraction recommendation results.
Methods
Definition and framework
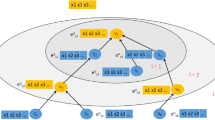
TMS-Net is a multilayer neural network prediction model designed to process route data and sequence information, providing personalized route recommendations for tourists with varying preferences. In this study, travel data is denoted as \(\:X\:=\:\left\{{x}_{1},{x}_{2},\:…,\:{x}_{k}\right\}\), where\(\:\:{x}_{i}(1\:\le\:\:i\:\le\:\:K)\) represents the feature set of tourists at a given scenic spot, which includes parameters such as latitude, longitude, altitude, time, and speed. The predicted results are denoted as \(\:Y\:=\:\{{y}_{1},\:{y}_{2},\:…,\:{y}_{k}\}\), where\(\:{\:y}_{i}\left(1\:\le\:\:i\:\le\:\:K\right)\) represents the feature set of tourists at the next scenic spot.
Figure 1 illustrates the framework of TMS-Net, which comprises five interconnected modules: the route encoding, time-series attention, multilayer LSTM neural network, feedforward neural network, and route prediction output modules.
Route coding module
TMS-Net uses sine and cosine functions to generate positional codes from the original data, enhancing the comprehension and generalization of the sequence of data while distinguishing between different types of positional information. Location coding provides a more concise, continuous, and periodic representation compared to one-hot coding, which maps each ___location or category to a separate vector. Each encoded vector represents a segment of the journey, with each position x and dimension \(\:i\) represented by the positional codes \(\:PE\_\left\{\right(pos,\:{2}_{i}\left)\right\}\) and \(\:PE\_\left\{\right(pos,\:{2}_{i+1}\left)\right\}\), respectively. Position \(\:p\) is described by a vector in the\(\:{\:d}_{model\:}\)dimension. Once the input sequence data are encoded, they are integrated into the information vector for each attraction feature. The resulting output then serves as the input for the subsequent TMS-Net module.
The route encoding module is crucial for enhancing the reliability of travel route recommendations. Figure 2 illustrates the consecutive routes of tourists visiting various attractions, each identified by a unique numerical identifier (ID). The entire travel path was encoded for route analysis. First, we integrated and recorded the geographic information of scenic spots, and then generated continuous ___location codes using sine-cosine functions. TMS-Net then calculated the continuous vector using a dimension matrix [0.1, 0.2] and sine-cosine functions. A concatenation function was employed to aggregate different feature vectors in series, forming the information vector for each scenic spot. This vector was subsequently input into the time-series attention module of TMS-Net. Ultimately, behavioral learning of tourist sequences was performed for a comprehensive analysis.
Route coding procedure (the maps were generated using QGIS software, version 3.28.14-Firenze, available at: https://qgis.org/). Each tourist attraction is identified by a unique numerical ID, and the complete travel itinerary of visitors is recorded. By integrating the geographical information of each attraction, continuous position encodings are generated using sine and cosine functions, resulting in continuous vectors recognizable by TMS-Net.
Time-series attention mechanism
The self-attention mechanism in TMS-Net incorporates relative positional information, enhancing its ability to capture the temporal relationships between tourist routes. In contrast to the traditional attention mechanism introduced by Transformer, which achieves parallelism by discarding the order of inputs, TMS-Net retains the contextual information of adjacent landmarks, which is essential for modeling travel routes. By ignoring input order, Transformer-based methods become unable to model relative positions within a sequence, leading to gaps in understanding travel routes. The time-series attention mechanism calculates attention scores based on the features of travel routes, maintaining complete sequence relationships regardless of the length of the sequence.
Time series attention mechanism. The attention mechanism first computes the dot product of each element with all other elements, resulting in an initial relevance score. Subsequently, positional offsets are introduced to enhance the model’s ability to distinguish between elements at different positions. Then, the SoftMax function is applied to normalize these relevance scores, yielding a set of attention weights. These weights reflect the importance of each element in processing the current input, enabling the model to focus on the most relevant information.
Figure 3 illustrates the framework of time-series attention mechanism. The attention mechanism calculates the attention score by determining the similarity between one element and all others in the sequence through a dot product operation. For a set of travel data\(\:\:X\:=\:\left\{{x}_{1},{x}_{2},\:…,\:{x}_{k}\right\}\), the attention score between elements \(\:{x}_{i\:}\)and \(\:{x}_{j\:}\)is calculated as
In this study, we incorporated the positional offset (relative position) into the attention score calculation. Assuming element\(\:\:{\:x}_{i\:}\:\)and \(\:{y}_{i\:}\)represent the positions of two elements, with \(\:{\:r}_{ij\:}\)as their relative positional difference, and d as the embedding dimension, the updated attention score is expressed as
The attention weights, calculated by applying the softmax function to the attention scores, indicate the importance of each element relative to others in the sequence. The attention weight for element \(\:{x}_{i\:}\:\)to element\(\:{\:x}_{j\:}\)is
The output of element \(\:{x}_{i\:}\), resulting from the weighted sum of the input sequence using attention weights, is obtained as
Multilayer LSTM neural network module
To mitigate the loss of temporal information in tourist trajectory data and ensure the coherence in the generated tourist routes, we implemented a multilayer LSTM neural network. This module integrates features of tourist routes into the time steps of TMS-Net, enabling it to capture long-term dependencies and dynamic patterns in travel data. Figure 4 illustrates how the multilayer LSTM neural network module helps TMS-Net learn the relationships between consecutive time steps by weighting the hidden states over. This process allows the model to better understand the travel intentions of the tourist.
Multilayer LSTM neural network. Each time step contains not only basic information such as position and altitude but also dynamic features related to time series. The cell state serves as the long-term memory of the network, ensuring the continuity and effectiveness of information across long sequences. In contrast, the hidden state acts as the short-term memory of the network, capturing and retaining the output information from the previous time step. The multi-layer Long Short-Term Memory (LSTM) network effectively remembers and updates these key pieces of information through the interplay of cell states and hidden states.
Each time step in the travel data contains ___location-based information. When these data are incorporated into the multilayer LSTM neural network structure, \(\:{c}_{t\:}\)represents the cell state at the current time step, whereas the hidden state \(\:{h}_{t\:}\)and cell state\(\:\:{\:c}_{t-1\:}\)capture information from the previous time step. \(\:{g}_{t\:}\)represents the candidate cell state for the current time step, and is gradually updated over time.
TMS-Net regulates the importance of current inputs and how much historical information should be retained or discarded at each time step. In addition, it controls the output information at each specific moment, where \(\:{p}_{t\:},\:{e}_{t\:},\:and\:{v}_{t\:}\:\)represent the ___location, elevation, and other input features, respectively, and \(\:{i}_{t\:},{f}_{t\:},\:and\:{o}_{t\:}\:\)are the activation vectors for various gating types.
Experiment
Data processing
This study collected travel data from tourists in Chengdu, Sichuan Province, between January 2016 to December 2022. The data were sourced from Flickr (https://www.flickr.com/), a platform rich in user-generated travel information, making it suitable for research on travel route recommendations. The extracted features included the user ID, longitude, latitude, altitude, speed (km/h), and total distance traveled. To ensure the optimal performance of TMS-Net, the original travel data were preprocessed.
-
Tourist travel records in Chengdu and surrounding areas were filtered based on longitude and latitude.
-
Continuous route data were organized by time and ___location to ensure only one record was retained at the same ___location and time.
-
Data points were identified as potential tourist attractions based on their latitude, longitude, speed, and altitude.
-
Data spanning more than 7 d were excluded.
After preprocessing, the dataset included more than 120 scenic spots and over six million tourist routes in Chengdu. Figure 5 shows the filtered travel data, with most points concentrated in central Chengdu and a smaller number in surrounding areas.
To reduce data redundancy, this study utilized a time-aggregation algorithm to extract representative features from the travel data, ensuring that each TMS-Net input contained a continuous route dataset for a single tourist. First, the time interval for each scenic spot was set to 1 h, and multiple raw data entries were consolidated into datasets for different time intervals. A small time interval could lead to overfitting, whereas an overly large interval might result in the loss of important information. The data within each time interval were aggregated using the mean value, and the aggregated result, along with the original timestamp, represented information on continuous visits to the scenic spot across multiple intervals. After merging all aggregated datasets, a more representative and interpretable dataset was generated using the time-aggregation algorithm.
Figure 6 illustrates the tourist route tracks retained after applying the time-aggregation algorithm, encompassing over 90 tourist attractions and 100,000 valid tourist route data points.
Experimental settings
Model comparison
The TMS-Net model integrates multiple fundamental deep learning models. To evaluate the practical effectiveness of this model ensemble, as shown in Table 4. To evaluate the practical effectiveness of this model ensemble, comparative experiments were conducted with several popular models, including Bidirectional Long Short-Term Memory (Bi-LSTM), Gated Recurrent Unit Long Short-Term Memory (GRU-LSTM), and Temporal Interaction Multiscale Network (Times-Net). Additionally, we compared the multilayer LSTM neural network and the time-series attention mechanism within TMS-Net through experiments to investigate the effectiveness of the TMS-Net modules.
Evaluation metrics and experimental environment
This experiment employed several evaluation metrics, including Recall, Precision, Haversine, root mean squared error (RMSE), mean squared error (MSE), and R2. Recall and Precision were used to assess the coverage and accuracy of the recommendation system concerning real user preferences. Haversine, RMSE, and MSE were applied to evaluate the performance of the ___location prediction task by measuring the spherical distance, RMSE, and MSE between the predicted and actual positions. R2 was used to determine how well the model fit the data. Combining the results of these evaluation metrics comprehensively assessed the performance of the recommendation system and accuracy of the prediction task.
The Haversine formula accurately calculates the spherical distance between two points on the Earth’s surface using their latitudes and longitudes, which is crucial for verifying the distance between predicted and actual attraction coordinates. A smaller Haversine distance between the predicted and actual coordinates indicates better model performance, whereas, a larger distance suggests prediction errors that require further optimization.
The formula for Haversine distance is
where d is the distance between two points, \(\:r\:\)is the radius of the Earth, \(\:\varDelta\:lat\) is the difference in latitude, \(\:\varDelta\:lon\) is the difference in longitude, and lat1 and lat2 are the latitudes of points 1 and 2, respectively.
The comparative experiment was conducted five times, with the final score calculated as the average value. The experiments were tested using Python 3.10 and TensorFlow 1.8 on a platform equipped with an Intel (R) Core (TM) [email protected] GHz processor and an NVIDIA GeForce RTX 4060 graphics card.
Model evaluation
Table 5 presents the experimental results for multi-model travel route prediction. Recall and Precision were used to assess the accuracy and reliability of the models in predicting travel routes. Times-Net and Bi-LSTM and model performed poorly, with low Recall and Precision, indicating its limited ability to capture real travel routes. Although GRU-LSTM model showed some improvement, its performance was still not optimal. Conversely, the TMS-Net model demonstrated significantly superior performance in both Recall and Precision than the other models.
In terms of fundamental deep learning models. The Haversine distance, RMSE, and MSE were used to evaluate the disparity between predicted and actual routes. The experimental results indicate that the LSTM model has limitations, including a tendency to overfit, a lack of interpretability, and inadequacy in handling long-term dependencies in tourism route planning. In contrast, the Autoregressive Moving Average (ARMA) model assumes data linearity, making it difficult to capture complex nonlinear patterns; it is also best suited for stationary data, performing less effectively with dynamically changing tourism route data. Additionally, models such as Deep Move and Personalized Weight Propagation perform well on these metrics but still could not match the performance of TMS-Net. Furthermore, the R2 index was used to evaluate data fitting. TMS-Net had the highest R2 value, indicating that it explained data variation more effectively than Bi-LSTM and GRU-LSTM, which exhibited weaker fitting capabilities.
In summary, the TMS-Net model outperformed all other models for accuracy, reliability, and data fitting for travel route prediction. The multilayer LSTM neural network and time-series attention mechanism integrated within TMS-Net were key factors in improving overall performance.
Sensitivity analysis
Impact of time interval size
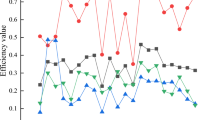
The selection of the time intervals directly affects the accuracy and stability of TMS-Net. As shown in Fig. 7a, different time intervals yield varying prediction scores. When the interval was too long, TMS-Net overlooked important details and turning points during travel, leading to inaccurate recommendations and reduced user satisfaction. Conversely, a very short time interval led to overinterpreting travel behaviors, mistaking brief stops or minor activities for significant events, thereby introducing noise and affecting prediction stability. Through a comparative analysis of the results produced by TMS-Net under different time intervals, we determined the optimal interval to be between 0.8 and 1.2 h. TMS-Net captured key information and activity changes within this range, effectively addressing the needs of various trip types and user preferences.
Influence of track length
Figure 7b illustrates the effects of the input and output trajectory lengths on the prediction scores. The input trajectory contained past travel data, whereas the output trajectory determined recommended attractions. As input trajectory length increased, the model learned from a broader dataset, enhancing its understanding of behavioral patterns and preferences. However, beyond a certain point, further increases in input length provided minimal additional benefit, leading to model stability. For the output trajectory, moderate lengths yielded the highest scores, as tourists could visit only a limited number of attractions within a given time. While longer output trajectories stabilized the generated routes, further extension had minimal effect on improving stability and instead added to the cognitive load on users, potentially reducing their experience.
Overall, the prediction results of the model stabilized when the input and output trajectories reached optimal lengths. This indicates that incorporating the multilayer LSTM neural network and time-attention mechanism significantly improved the exploration of correlations between scenic spots. By adjusting trajectory lengths, the model effectively balanced predictive performance with user experience.
Example analysis
Travel records from the training dataset were randomly selected for further analysis, where TMS-Net predicted the next destinations based on the last visited ___location of the tourists. A correlation coefficient matrix was used to visualize the time-attention mechanism and highlight the influence weights of each destination.
Sensitivity analysis. Sensitivity analysis was conducted from two aspects: Impact of Time Interval Size and Influence of Track Length. (a) (filled blue square—Recall, filled orange triangle—Precision) illustrates the trend of the impact of different time intervals on the prediction results, identifying the optimal time interval value as 0.8 to 1.2 h. (b) (filled blue square—Recall, filled orange triangle—Precision) shows the influence of input and output trajectory lengths on the prediction results, concluding that both excessively long and excessively short trajectory lengths are detrimental to the model’s training.
The heat maps of influence weights of scenic spots. The time attention mechanism is visualized using a correlation coefficient matrix, allowing the importance of attractions within the trajectories to be discerned by observing the depth of the colors. The deeper the color, the higher the importance of the attraction.
As shown in Fig. 8, the numbers in the heatmap matrix correspond to various attractions. By analyzing the color depth, TMS-Net can intuitively identify the most significant attractions in historical trajectories. When travel data are processed through the temporal attention mechanism, the model considers route selection based on the itineraries of the travelers. The visit sequence and distances between attractions are integrated into the calculation as key temporal attention weight factors, capturing associations between them. Additionally, adjusting the attraction weights within the matrix further optimizes the learning and predictive capabilities of TMS-Net, enhancing the accuracy and practicality of its predictions.
The FP-growth algorithm was used to verify the predicted routes against the actual routes, calculating the weight of each scenic spot. The color range around a spot indicates its influence weight, with a wider range reflecting a greater weight. For example, attraction 132 was linked with attractions 128 and 96, likely owing to their proximity and the frequency of past visits, which affected the prediction results. As shown in Fig. 9, after selecting attraction 132, the recommended subsequent attractions include 96, 105, and 23. The final selection depends on the cyclic judgment for subsequent attraction predictions. In summary, the combination of the time-attention mechanism and scenic spot characteristics enhances the decision-making process within the interpretable prediction logic of TMS-Net, improving tourist route predictions and services.
Figure 10 depicts both correct ((a) and (b)) and incorrect ((c) and (d)) prediction cases. The black line represents the historical trajectory of the traveler, whereas the blue and red lines represent the actual and predicted routes, respectively. Incorrect predictions may result from errors or missing critical travel data, reducing the ability of TMS-Net to capture user behavior patterns and preferences. In addition, an incomplete understanding of the travel industry and target user groups in the training data may contribute to prediction errors. Nonetheless, TMS-Net demonstrated relatively strong predictive capabilities at this stage.
Physical trajectory of the travel route and FP-growth weight results(the maps were generated using QGIS software, version 3.28.14-Firenze, available at: https://qgis.org/). A tourist route trajectory was extracted from the dataset, and the FP-growth algorithm was employed to calculate the associations between attractions. The range of colors surrounding each attraction represents its influence weight, with a wider range indicating a greater weight.
Example of a TMS-Net forecast route (the maps were generated using QGIS software, version 3.28.14-Firenze, available at: https://qgis.org/). Both correct ((a) and (b)) and incorrect ((c) and (d)) prediction cases. The black line represents the historical trajectory of the traveler, whereas the blue and red lines represent the actual and predicted routes, respectively.
Recommended routes
The analysis in this study was based on the routes recommended by TMS-Net. Figure 11 shows the popular tourist routes for attractions in Chengdu.
-
Figure 11a depicts the historical and cultural route in Chengdu, highlighting its rich heritage through attractions such as the Wuhou Shrine, Chengdu Museum, Kuanzhai Alley, and Du Fu Thatched Cottage.
-
Figure 11b shows a natural scenery route around Chengdu, featuring destinations such as Qingcheng Mountain, the Dujiangyan Irrigation System, Tongma Gou Bamboo Sea Park, and Yinxiu Bay Park.
-
Figure 11c illustrates a modern urban route in downtown Chengdu, including landmarks such as Tianfu Square, Chunxi Road, Chengdu TV Tower, and Chenghua Park.
-
Figure 11d presents a family-friendly route for parents and children, with attractions such as the Chengdu Research Base of Giant Panda Breeding, Happy Valley Amusement Park, Chengdu Haichang Polar Ocean Park, Guose Tianxiang Paradise, and the Botanical Garden.
Recommended travel routes in Chengdu (the maps were generated using QGIS software, version 3.28.14-Firenze, available at: https://qgis.org/). Based on the model’s prediction results, four distinct tourist routes in Chengdu were summarized: (a) depicts the historical and cultural route in Chengdu; (b) shows a natural scenery route around Chengdu; (c) illustrates a modern urban route in downtown Chengdu; (d) presents a family-friendly route for parents and children.
Discussion
TMS-Net effectively addresses the challenges of segmenting travel time and extracting personalized tourist preferences. Introducing a time-attention mechanism based on relative positional information enables TMS-Net to capture the temporal relationships between different locations accurately. The multilayer LSTM neural network further enhances the model by learning from historical travel paths, avoiding recommendations of outdated or irrelevant routes. Furthermore, TMS-Net dynamically adjusts recommendations based on factors such as visit timing and frequency. For instance, the model avoids suggesting another restaurant to a user who has recently visited one, thereby enhancing the relevance and personalization of the user experience. Compared to other popular time-series models, TMS-Net excels in both attraction prediction and route planning. A key example is the classic tourist route in Chengdu, Sichuan Province, proposed by the model. The overall framework of TMS-Net, from data acquisition to route recommendation, aligns well with smart tourism development. As the dataset increases, the potential to train the model with richer tourist features will increase. For instance, users interested in cultural relics could receive recommendations for historically significant sites, whereas those who prefer outdoor adventures could be directed to scenic natural attractions.
Conclusion
Personalized route recommendations based on historical travel trajectories and tourist preferences have become a key area of research. This study introduces TMS-Net, a multilayer neural network model designed to process route data and sequence information for personalized travel recommendations. Future research will expand this study by incorporating multimodal analysis, using neural networks to integrate various data types, such as videos, images, and text. Videos can capture dynamic scenes and the atmosphere of tourist destinations, images can offer high-resolution details, and text can reflect the preferences and historical behaviors of users. In the process of recommendation, TMS-Net will integrate access time and contextual information to prevent the repetitive recommendation of similar locations within a short time span. By combining these diverse data sources, TMS-Net will enrich its recommendation capabilities. This approach will enable TMS-Net to provide more tailored travel recommendations based on deeper insights into the interests and behaviors of tourists, further advancing the potential of smart tourism.
Data availability
Data is available upon request. Please contact the corresponding author by email to obtain the data used in the study.Data is available upon request. Please contact the corresponding author by email to obtain the data used in the study. The maps were generated using QGIS software, version 3.28.14-Firenze, available at: https://qgis.org/.
References
Del Vecchio, P., Mele, G., Ndou, V. & Secundo, G. Creating value from social big data: implications for smart tourism destinations. Inf. Process. Manag. 54, 847–860. https://doi.org/10.1016/j.ipm.2017.10.006 (2018).
Zatori, A., Smith, M. K. & Puczko, L. Experience-involvement, memorability and authenticity: the service provider’s effect on tourist experience. Tour. Manag. 67, 111–126. https://doi.org/10.1016/j.tourman.2017.12.013 (2018).
Cui, Z. et al. Personalized recommendation system based on collaborative filtering for IoT scenarios. IEEE Trans. Serv. Comput. 13, 685–695. https://doi.org/10.1109/tsc.2020.2964552 (2020).
Jain, P. K., Pamula, R. & Srivastava, G. A systematic literature review on machine learning applications for consumer sentiment analysis using online reviews. Comput. Sci. Rev. 41 https://doi.org/10.1016/j.cosrev.2021.100413 (2021).
Liu, Y. et al. Interaction-enhanced and time-aware graph convolutional network for successive point-of-interest recommendation in traveling enterprises. IEEE Trans. Industr. Inf. 19, 635–643. https://doi.org/10.1109/tii.2022.3200067 (2023).
Wu, L., He, X., Wang, X., Zhang, K. & Wang, M. A survey on accuracy-oriented neural recommendation: from collaborative filtering to information-rich recommendation. IEEE Trans. Knowl. Data Eng. 35, 4425–4445. https://doi.org/10.1109/tkde.2022.3145690 (2023).
Jeong, M. & Shin, H. H. Tourists’ experiences with smart tourism technology at smart destinations and their behavior intentions. J. Travel Res. 59, 1464–1477. https://doi.org/10.1177/0047287519883034 (2020).
Li, X., Pan, B., Law, R. & Huang, X. Forecasting tourism demand with composite search index. Tour. Manag. 59, 57–66. https://doi.org/10.1016/j.tourman.2016.07.005 (2017).
Wu, Y., Li, K., Zhao, G. & Qian, X. Personalized long- and short-term preference learning for next POI recommendation. IEEE Trans. Knowl. Data Eng. 34, 1944–1957. https://doi.org/10.1109/tkde.2020.3002531 (2022).
Zhao, P. et al. Where to go next: a spatio-temporal gated network for next POI recommendation. IEEE Trans. Knowl. Data Eng. 34, 2512–2524. https://doi.org/10.1109/tkde.2020.3007194 (2022).
Lara-Benitez, P., Carranza-Garcia, M. & Riquelme, J. C. An experimental review on deep learning architectures for time series forecasting. Int. J. Neural Syst. 31 https://doi.org/10.1142/s0129065721300011 (2021).
Torres, J. F., Hadjout, D., Sebaa, A., Martinez-Alvarez, F. & Troncoso, A. Deep learning for time series forecasting: a survey. Big Data. 9, 3–21. https://doi.org/10.1089/big.2020.0159 (2021).
Yang, B., Lei, Y., Liu, J. & Li, W. Social collaborative filtering by trust. IEEE Trans. Pattern Anal. Mach. Intell. 39, 1633–1647. https://doi.org/10.1109/tpami.2016.2605085 (2017).
Zhang, Y., Yin, C., Wu, Q., He, Q. & Zhu, H. Location-aware deep collaborative filtering for service recommendation. IEEE Trans. Syst. Man. Cybernetics-Systems. 51, 3796–3807. https://doi.org/10.1109/tsmc.2019.2931723 (2021).
Leibig, C., Allken, V., Ayhan, M. S., Berens, P. & Wahl, S. Leveraging uncertainty information from deep neural networks for disease detection. Sci. Rep. 7 https://doi.org/10.1038/s41598-017-17876-z (2017).
Ranjbarzadeh, R. et al. Brain tumor segmentation based on deep learning and an attention mechanism using MRI multi-modalities brain images. Sci. Rep. 11 https://doi.org/10.1038/s41598-021-90428-8 (2021).
Kulshrestha, A., Krishnaswamy, V. & Sharma, M. Bayesian BILSTM approach for tourism demand forecasting. Ann. Tour. Res. 83 https://doi.org/10.1016/j.annals.2020.102925 (2020).
Sandfort, V., Yan, K., Pickhardt, P. J. & Summers, R. M. Data augmentation using generative adversarial networks (CycleGAN) to improve generalizability in CT segmentation tasks. Sci. Rep. 9 https://doi.org/10.1038/s41598-019-52737-x (2019).
Law, R., Li, G., Fong, D. K. C. & Han, X. Tourism demand forecasting: a deep learning approach. Ann. Tour. Res. 75, 410–423. https://doi.org/10.1016/j.annals.2019.01.014 (2019).
Chen, R., Liang, C. Y., Hong, W. C. & Gu, D. X. Forecasting holiday daily tourist flow based on seasonal support vector regression with adaptive genetic algorithm. Appl. Soft Comput. 26, 435–443. https://doi.org/10.1016/j.asoc.2014.10.022 (2015).
Zhang, K., Chen, Y. & Li, C. Discovering the tourists’ behaviors and perceptions in a tourism destination by analyzing photos’ visual content with a computer deep learning model: the case of Beijing. Tour. Manag. 75, 595–608. https://doi.org/10.1016/j.tourman.2019.07.002 (2019).
Ma, Y., Xiang, Z., Du, Q. & Fan, W. Effects of user-provided photos on hotel review helpfulness: an analytical approach with deep leaning. Int. J. Hospitality Manage. 71, 120–131. https://doi.org/10.1016/j.ijhm.2017.12.008 (2018).
Li, W., Zhu, L., Shi, Y., Guo, K. & Cambria, E. User reviews: sentiment analysis using lexicon integrated two-channel CNN-LSTM family models. Appl. Soft Comput. 94 https://doi.org/10.1016/j.asoc.2020.106435 (2020).
Lum, P. Y. et al. Extracting insights from the shape of complex data using topology. Sci. Rep. 3 https://doi.org/10.1038/srep01236 (2013).
Hu, Y. et al. Extracting and understanding urban areas of interest using geotagged photos. Comput. Environ. Urban Syst. 54, 240–254. https://doi.org/10.1016/j.compenvurbsys.2015.09.001 (2015).
Colladon, A. F., Guardabascio, B. & Innarella, R. Using social network and semantic analysis to analyze online travel forums and forecast tourism demand. Decis. Support Syst. 123 https://doi.org/10.1016/j.dss.2019.113075 (2019).
Colak, S., Lima, A. & Gonzalez, M. C. Understanding congested travel in urban areas. Nat. Commun. 7 https://doi.org/10.1038/ncomms10793 (2016).
Wang, W. et al. Realizing the potential of internet of things for smart tourism with 5G and AI. IEEE Netw. 34, 295–301. https://doi.org/10.1109/mnet.011.2000250 (2020).
Liang, S. B., Jiao, T. T., Du, W. C. & Qu, S. M. An improved ant colony optimization algorithm based on context for tourism route planning. PLoS ONE. 16 https://doi.org/10.1371/journal.pone.0257317 (2021).
Guo, M. H. et al. Attention mechanisms in computer vision: a survey. Comput. Visual Media. 8, 331–368. https://doi.org/10.1007/s41095-022-0271-y (2022).
Zhao, G. S., Lou, P. L., Qian, X. M. & Hou, X. S. Personalized ___location recommendation by fusing sentimental and spatial context. Knowl. Based Syst. 196 https://doi.org/10.1016/j.knosys.2020.105849 (2020).
Zheng, X. & Chen, W. Z. An attention-based Bi-LSTM method for visual object classification via EEG. Biomed. Signal Process. Control. 63 https://doi.org/10.1016/j.bspc.2020.102174 (2021).
Zheng, H. F., Lin, F., Feng, X. X. & Chen, Y. J. A hybrid deep learning model with attention-based Conv-LSTM networks for short-term traffic flow prediction. IEEE Trans. Intell. Transp. Syst. 22, 6910–6920. https://doi.org/10.1109/tits.2020.2997352 (2021).
Huo, Y., Wong, D. F., Ni, L. M., Chao, L. S. & Zhang, J. J. I. S. Knowledge modeling via contextualized representations for LSTM-based personalized exercise recommendation. 523, 266–278 (2020).
Lika, B., Kolomvatsos, K. & Hadjiefthymiades, S. Facing the cold start problem in recommender systems. Expert Syst. Appl. 41, 2065–2073. https://doi.org/10.1016/j.eswa.2013.09.005 (2014).
Cao, S. An optimal round-trip route planning method for tourism based on improved genetic algorithm. Comput. Intell. Neurosci. 2022 https://doi.org/10.1155/2022/7665874 (2022).
Ke, J., Zheng, H., Yang, H. & Chen, X. Short-term forecasting of passenger demand under on-demand ride services: a spatio-temporal deep learning approach. Transp. Res. Part. C-Emerg. Technol. 85, 591–608. https://doi.org/10.1016/j.trc.2017.10.016 (2017).
Chang, I. C., Tai, H. T., Yeh, F. H., Hsieh, D. L. & Chang, S. H. A VANET-based A* route planning algorithm for travelling time- and energy-efficient GPS navigation app. Int. J. Distrib. Sens. Netw. https://doi.org/10.1155/2013/794521 (2013).
Zeng, C., Ma, C. X., Wang, K. & Cui, Z. H. Parking occupancy prediction method based on multi factors and stacked GRU-LSTM. IEEE Access. 10, 47361–47370. https://doi.org/10.1109/access.2022.3171330 (2022).
Acknowledgements
This work was supported by the Yibin University Social Science Project (Nos.2022PY02),and the Project of Sichuan Provincial Innovation Nature of Science and Technology (No.2021ZFSF011/001).
Author information
Authors and Affiliations
Contributions
XueFei Xiao and ChunHua Li led the analysis and writing of this paper. All authors read and contributed to the drafing of the paper. XingJie Wang did the interpretation of the data. AnPing Zeng conceived and designed the experiment. All authors reviewed the manuscript and approved the publication of our manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Xiao, X., Li, C., Wang, X. et al. Personalized tourism recommendation model based on temporal multilayer sequential neural network. Sci Rep 15, 382 (2025). https://doi.org/10.1038/s41598-024-84581-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-84581-z