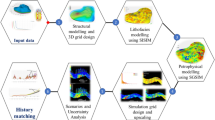
Abstract
The incompleteness of data and the variability in research methodologies can lead to significant uncertainties in reservoir modeling predictions. Effectively reducing and assessing these uncertainties are central issues in reservoir modeling studies. This research takes the ultra-low permeability and ultra-low porosity conglomeratic sandstone oil reservoir in the Yong 935–936 block of the Dongying Depression as a case study to conduct a survey on uncertainty modeling and evaluating. Considering the presence of multiple sediment sources in the study area, a variogram model with local variable azimuth angles is designed to address the discontinuity of sand bodies at the partition boundaries during modeling. Geological insights are used to delineate the boundaries of fan bodies, and statistical analysis of the proportions of sandstone and mudstone under different effective reservoir property limits within these fan bodies provides conditional data to reduce uncertainties in the modeling process. A full-factor experiment is conducted to perform a sensitivity analysis on parameters influencing reserves calculations, clarifying the significance of various influencing factors, such as fan body boundaries, effective reservoir property thresholds, and variogram range. A multivariate regression model between reserves calculation and significant influencing factors is constructed through response surface experiments. Finally, combining the Monte Carlo random simulation method, the distribution of cumulative probability reserves is obtained, and the 3P reserves of the study area are predicted to test the effectiveness of the multivariate regression model.
Similar content being viewed by others
Introduction
The reservoir is formed under the combined influence of various factors such as structure, sedimentation and diagenesis. The uncertainty and stochasticity of the reservoir modeling are inevitable when it is constructed based on the limited data such as well logging and seismic data1,2,3. An important step in reservoir modeling is to build reservoir models that conform to the current cognition, minimize the uncertainty in modeling and evaluate the uncertainty of the model.
The uncertainty in the model can be categorized into response uncertainty, spatial uncertainty and local uncertainty4. The local uncertainty can be characterized by plotting the cumulative probability curve5. The spatial uncertainty can be described by using Euclidean distance or by using the correct point-to-percentage method in the scatter plot6,7. By constructing target models with different modeling methods and comparing the characteristics of standard deviation of simulation results under different conditions, the response uncertainty can be characterized8. Additionally, response uncertainty can also be quantified by variance analysis9,10.
The application of the processed seismic data to the model construction can effectively reduce the uncertainty of the model11,12. The adoption of new technical means to collect data can also minimize uncertainty13. Additionally, using higher-order modeling methods, such as multi-point geostatistics, can also effectively reduce the uncertainty14,15. Furthermore, using reservoir numerical simulation to verify and adjust the model, the uncertainty of the model can also be effectively reduced14,16.
Modeling by well pattern sparsing is a common evaluation method for model evaluating17, and it is also a desirable method to verify the model by means of three-dimensional probability distribution18. The introduction of experimental design methods, commonly used in medical research, has significantly improved the rationality of model verification and uncertainty evaluation19,20,21. Once the uncertain sources and evaluation factors in the modeling process are clearly defined, the uncertainty factors affecting the modeling results can be quantitatively analyzed through reasonable experiment design, and a suitable reservoir model can be selected22,23,24,25,26.
After identifying the main sources of uncertainty, this study quantitatively evaluates the uncertainty factors in the modeling process through the method of experimental design, ultimately optimizes the appropriate target model.
Geological setting
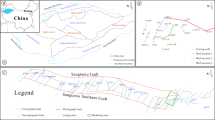
The study area is located in Xizhang Town, Kenli County, Dongying City, Shandong Province. It is structurally located in the south of Chenan fault and the north of Lijin-Binnan fault system. It is located in the first and second steps of the structural slope break belt, which is bordered to the west by the Binxian Uplift, to the north by the Chenjiazhuang Uplift, to the south by the Lijin oil-generating depression, and to the east by the Qingtuozi Uplift (Fig. 1).
The structure of the study area is relatively simple. To the west, the terrain is characterized by higher elevations in the north and lower elevations in the south, while to the east, it is high in the northeast and low in the southwest. The oil reservoir presents a trend of oil-bearing linkage from west to east, and the main oil-bearing sand body is the conglomerate complex fan in the near-shore underwater fan, located within the steep slope zone of the faulted lacustrine basin in the fourth member of Shahejie Formation. The internal lithology of the sand-gravel rock mass is complex, reflecting multi-stage rapid accumulation or re-collapse field deposition27,28. The electrical properties of the reservoir are greatly affected by the tight conglomerate. Core analysis showed that the porosity was concentrated in the range of 5.3-13.5% with an average of 7.8% (Fig. 2), and the permeability was 0.72 × 10 − 3µm2 to 39.07 × 10 − 3µm2 with an average of 4.2 × 10 − 3µm2 (Fig. 3). Due to the deep burial, the effective and non-effective reservoir are mixed, and the heterogeneity is serious. As a result, it is classified as an ultra-low porosity and ultra-low permeability reservoir.
According to the previous analysis of the source of ancient gully sediments in the sedimentary period of the upper submember of the fourth member of Shahejie Formation, there are three primary directions of source in the study area, which are the northern source, the lateral source in the west and the eastern source, which are typical multi-source deposition29,30,31.
Materials and methods
Partition blocks
The seismic response characteristics across different zones of the study area are distinctly different. In the root area of the fan delta, the reservoir is thick with almost no shale, exhibiting broad and weak reflections, without distinct reflection axes or with reflection axes of large dip angles. In the middle area of the fan delta, the reservoir is relatively thick, with mudstone layers showing strong reflections and poor continuity. In the distal area of the fan delta, the reservoir is even thinner, with developed shale leading to local strong reflections and poor continuity(Fig. 4). In the pure shale areas, reflections are clear and continuous. Based on these observations, seismic facies patterns are established to provide a comprehensive basis for the subsequent boundary delineation of the fan body.
Based on the seismic division of blocks, more detailed boundary delineation can be achieved by analyzing the sand body thickness. In the study area, the effective reservoir is located in the fan middle facies zone, while the poor reservoir is in the fan root facies zone. The reservoir quality in the fan middle facies zone is significantly better than that in the fan root facies zone. Therefore, the primary focus is on the stratigraphic thickness of the fan middle zone. Analysis reveals that there are two thickness centers in the study area. In the western Yong935 area, influenced by a sediment source direction approximately from the north-northeast, the effective thickness is relatively thin in the 7th stage. The center of the fan middle zone’s stratigraphic thickness is located to the north of the Yong928C well, with a maximum thickness of 60 m. In the 8th stage, the center of the stratigraphic thickness shifts, roughly toward the northeast of the Yong928C well, with a maximum thickness of 240 m. In the eastern Yong936 area, influenced by a northward sediment source, the stratigraphic thickness is greater in the 7th stage, with the thickest center located near the Yong936 well, reaching a maximum thickness of 260 m. In the 8th stage, however, the stratigraphic thickness in the Yong936 area decreases significantly, shrinking to 140 m, and the center of the thickness shifts toward the northwest (Fig. 5).
Finally, integrating seismic insights and stratigraphic thickness, the boundaries of the fan bodies are delineated, dividing the study area into the eastern Yong 936 region, the central region, and the western Yong 935 region. Considering that defining a single boundary involves certain subjectivity and uncertainty, which cannot objectively represent the fan body boundary characteristics, the original boundaries were appropriately expanded and contracted. Three different boundary levels were established: pessimistic, optimistic, and most likely (Fig. 6). These boundaries serve as the foundation for subsequent construction of sand-mud facies models and attribute models.
Collect sand-mud ratio
Within the study area, the lower limit of porosity is determined to be 4.7% and the lower limit of permeability is 0.7 mD using the forward and inverse cumulative method. The calculated lower limit of porosity is 5.3% and the permeability is 0.7 mD using the resistivity lower limit inversion method. Verification through core sampling and oil testing result in lower limit of porosity at 5.3% and a permeability of 1.6 mD. Selecting a single set of physical property limits as the criterion for evaluate sand-mud facies cannot effectively assess the impact of the effective property limits on the construction of sand-mud facies models and reserve calculations. Therefore, the physical property limits derived from the three methods are set as three different levels: Physical Property Lower Limit One, Physical Property Lower Limit Two, and Physical Property Lower Limit Three. Under the previously delineated three boundary conditions, different effective property limits are used to statistically determine the percentage of sand and mud within each sub-layer under different property limit conditions (Table 1). During the statistical process, when the percentage of mudstone facies reaches 100% under a given condition, the sand-mud ratio for that condition is set to 1.
Constructing conditional data
Constraint surface of azimuth
Due to the presence of multiple source directions in the study area, it is necessary to impose constraints on the azimuth of the variogram during the modeling process. Based on the defined boundaries of the western Yong935 area, the central area, and the eastern Yong936 area, and referencing the source analysis results, constraint surfaces for the source directions of the three regions were assigned. The sediment source direction in the Yong 935 area is 20° west of north, while in the Yong 936 area, it is oriented to the northeast. Therefore, the sediment source direction constraint for the Yong 935 area is set to 340°, and for the Yong 936 area, it is set to 45°. For the central region, the constraint is set to 0° (Fig. 7). For the three different levels of fan body boundary conditions, the same procedure is required to ensure that the azimuth data in the azimuth constraint files used for each boundary condition level are consistent.
Constraint surface of lithology proportion
By processing the statistically obtained sand-mud rock percentage data under different conditions, the sand-mud rock percentage data for the Yong 935 area, central region, and Yong 936 area in the study area can be effectively utilized. Taking the 7 − 1 sub-layer as an example (Fig. 8), under the pessimistic boundary and effective property limit one conditions, the mudstone% in the western Yong 935 area is 76.3% and the sandstone% is 13.7%; in the central region, the mudstone% is 78.4% and the sandstone% is 21.6%; in the eastern Yong 936 area, the mudstone% is 64% and the sandstone% is 36%. Surface files are generated using the boundaries of the western Yong 935 area, central region, and eastern Yong 936 area, and the statistically obtained sandstone proportion values are assigned to the surface files of the three regions. New surface files are then created for the three regions, and the statistically obtained mudstone proportion values are assigned to the surface files of the three regions, ensuring that on the vertical direction, the sum of the sandstone constraint surface file values and the mudstone constraint surface file values for a given area is 1. Figures 3, 4, 5, 6 and 7 illustrates the sandstone facies constraint surface file for the 7 − 1 sub-layer under the pessimistic boundary and property limit one conditions. Since the sand-shale percentages vary under different fan boundary conditions using various effective physical property lower limits, it is necessary to construct sand-shale facies constraint files for each small layer under different constraint conditions. These surface constraint files serve as conditional data for building lithofacies models.
Full factor experiment
In the preparation of basic condition data, the setting of boundaries affects the extent of the fan body, which in turn has a certain impact on the calculation of reserves. The physical property lower limits influence the statistical proportion of sand-mud rock within the boundaries, which in turn affects the construction of the lithofacies model and subsequent reserve calculations. Different variograms models affect the spatial relationships in the specific modeling, thereby impacting reserve calculations. Therefore, there are three main influencing factors during the experimental modeling process: boundaries, physical property lower limits, and variogram range. Based on the above analysis, a three-factor, three-level full-factorial experimental design can be developed as follows(Table 2):
Results
Models with constrained data
By combining boundary conditions, physical property lower limits, and variogram range conditions, 27 distinct sand-mud facies models are constructed by Petrel201832. Consistent with the overall characteristics reflected by the sand-mud ratio statistical parameters, the sand-mud rock percentages vary under different boundary conditions, and the proportion of sand-mud facies in the models differs accordingly. Under the same boundary conditions and effective reservoir property lower limits, the characteristics of the sand-mud facies models show similarities. However, when any of these conditions change, the characteristics of the constructed sand-mud facies models will change significantly.
Using the sand-mud ratio file obtained under optimistic boundary conditions and effective property lower limit one as constraints, the sand-mud facies models built with different variogram range conditions are analyzed (Fig. 9). Under these conditions, it was observed that the sandstone facies characteristics were not prominent in the 7th sub-layer of the western Yong 935 area, but were distinct and continuous in the 7th sub-layer of the eastern Yong 936 area. The sandstone facies characteristics under the three different range conditions were similar, but with minor differences in local areas. A comparison using histograms shows that the percentage of sand-mud facies fit under the three different variogram conditions differs only slightly. Under the pessimistic variogram condition, the sandstone facies accounted for 15.0% of the model, under the possible variogram condition, the sandstone facies accounted for 15.4%, and under the optimistic variogram condition, the sandstone facies accounted for 15.5%. The change in the percentage of sand-mud facies may be that as the range of the variogram increases, the variogram’s representation of the spatial structural characteristics of the sand-mud facies changes, leading to subtle differences in the final model.
Lithofacies model under conditions of optimistic boundary and lower limit32.
Models without constrained data
In contrast, when local variably constrained variograms are not applied, the characteristics of the sand-mud facies model in the study area change (Fig. 10). Spatially, the Yong 935 block in the west and the Yong 936 block in the east remain the primary distribution areas for sandstone facies, but the distribution of sandstone facies becomes more discrete. Cross-sectional observations reveal a significant abrupt change in the thickness of sandstone facies at the boundaries of the zones. Comparisons indicate that the lithofacies models constructed under the constraints of variograms with local variations are more consistent with geological understanding.
Lithofacies model without constraints of local variogram32.
Property model
After completing the data variation and variogram analysis for the physical property data, a facise-controlled modeling approach was adopted, using the facies model as the control constraint. The sequential Gaussian simulation method was used to construct the porosity model under different constraint conditions (Fig. 11a), while the permeability models(Fig. 11b) and water saturation(Fig. 11c) models were constructed under the constraint of the porosity model. All kinds of property models are constructed using Petrel201832.
Since the study area has two source directions, the direction was constrained by generating constraint surfaces. The preparation of the relevant constraint files has been discussed in the section on condition data processing. To enhance the reliability of subsequent reserve calculations, five corresponding physical property models were generated under the same facies model constraint.
The NTG model (Fig. 12) is obtained by calculating using the lower limit of Physical property lower limit. The calculation formula under the condition of lower limit 1 is formula1, under the condition of lower limit 2 is formula 2, under the condition of lower limit 3 is formula 3:
Propety model under conditions of optimistic boundary and lower limit32:(a) porosity model and (b) permeability model and (c) water saturation model.
NTG model under conditions of optimistic boundary and lower limit32.
Reserve calculation
The fundamental idea of applying a reservoir model to calculate reserves is to use the three-dimensional grid, defined during the modeling process, as the basic unit. Reserves are then calculated using Eq. 4, based on specific information within each grid, such as porosity, permeability, and water saturation.
Vbulk: Bulk Volume; NTG: Net to Gross Ratio; POR: Porosity;
SW: Water Saturation; Bo: Oil Formation Volume Factor。.
Under each facies model constraint, five corresponding physical property models were implemented, resulting in 135 reserve calculation values(Table 3). The final evaluation metric is the average reserve value for each facies model condition.
Uncertainty analysis
Full-factor experiment analysis
In the main effect diagram of the full-factor experiment (Fig. 13), under the pessimistic boundary conditions, the reserve value is the largest; under the possible boundary conditions, the reserve value is the smallest; and under the optimistic boundary conditions, the reserve value is in the middle. The reserves under the three boundary conditions do not exhibit a monotonically increasing or decreasing trend with the expansion of the boundaries, but rather show a pattern of decreasing first and then increasing as the boundaries expand. The reason for this characteristic is that as the boundaries increase, the area of the fan body also increases, and the corresponding statistical values of sand-mud percentages change accordingly. Under the possible boundary conditions, the percentage of sandstone reaches its minimum, leading to the smallest proportion of sandstone facies in the model, and the characteristics of the analysis results are consistent with the results of the lithofacies modeling.
Similarly, under the conditions of effective reservoir properties, the reserves are the smallest under pessimistic physical property lower limits and the largest under optimistic physical property lower limits. As the effective reservoir physical property lower limits change from optimistic to pessimistic, the reserve values also change from the largest to the smallest, showing a positive correlation between the trend of reserve values and the trend of effective reservoir physical property lower limits. The reason for this characteristic is that as the effective reservoir properties shift from an optimistic level to a pessimistic level, the lower limit values of effective reservoir properties increase, leading to a decrease in the percentage of sandstone, ultimately reducing the proportion of sandstone facies in the model, and thus decreasing the reserve calculation values.
In the range of variogram, when the range is at its minimum, the reserve value is also at its minimum, and when the range is at its maximum, the reserve value is at its maximum. The trend of reserve values shows a positive correlation with the increase in range. In the specific process of lithofacies modeling, as the range of the variogram increases, the spatial distribution range and connectivity of sandstone show a certain trend of improvement, which also well explains the characteristic in the analysis results that reserves increase with the increase in range.
The R-Sq statistics for the model based on analysis of variance, the predicted model, and the adjusted model are 98.82%, 86.61%, and 96.18% (Table 4). Respectively, the significance analysis of the factor analysis, shown in Fig. 14, indicates that boundary conditions and lower limit conditions are significant influencing factors. This is consistent with the information presented in the factor main effect plots and interaction plots above.
Response surface analysis
The full-factor experiment clarified that the boundary range and property lower limits have a significant impact on the mean value of reserve calculations. Therefore, in the response surface analysis, boundary range and property lower limits are selected as experimental factors. The appropriate variogram range is then adjusted to minimize its impact on reserve calculations, ensuring the stability of the calculation process. By modifying the boundary conditions and property lower limits, the optimal parameter combination is ultimately determined.
The experiment follows the principles of Central Composite Design (CCD), with the possible boundary and physical property lower limit two (POR > 5.3, PERM > 0.7) serving as the center points for response surface analysis. The levels of the two significant influencing factors are shown in Table 5. According to the principles of Central Composite Design, the experiment consists of 13 runs, with each run involving the construction of a facies model and three equiprobable physical property models, followed by the calculation of three reserve results. The final evaluation is based on the average value, and the experimental results are provided in Table 6.
Probabilistic reservoir simulation
The Monte Carlo simulation method was used for 1,000 reserve calculations, replacing the actual modeling and reserve calculation operations. By probability distribution graph (Fig. 15), the pessimistic reserve P10 is found to be 954.5 × 104 tons, the probable reserve P50 is 1059.7 × 10^4 tons, and the optimistic reserve P90 is 1164.9 × 104 tons.
Among the 1000 Monte Carlo simulation calculations, the reserve values close to the P10, P50, and P90 probability reserves are identified, and their corresponding variable values are converted to actual values. It is found that the influencing factor values for the P10 probability reserve are similar to those under the possible boundary and effective reservoir property limit three conditions. The influencing factor values for the P50 probability reserve are similar to those under the optimistic boundary and effective reservoir property limit two conditions. The influencing factor values for the P90 probability reserve are similar to those under the optimistic boundary and effective reservoir property limit one conditions. Models are constructed under these three sets of conditions using Petrel software, and reserves are calculated. Comparing the actual reserve calculation values with the Monte Carlo reserve prediction values, the errors are all less than 2%.
By performing a cross-analysis of the 13 calculated reserves with the 3P reserves (Fig. 16), a regression equation is obtained: Y = 1.042X − 42.71 (X is the model reserve and Y is the reserve calculated by the Monte Carlo or regression formula), with an R2 value of 0.986. This indicates that the multiple regression equation derived from the response surface experiment analysis has a certain degree of predictive ability. Additionally, combined with the Monte Carlo simulation method, it is possible to predict reserves under any conditions within the response surface.
Conclusions
This study takes the Yong 935–936 block of the Yanjia Oilfield in the Dongying Depression as an example. Aiming at the significant uncertainties present in the construction of a single geological reservoir model, three influencing factors affecting reservoir modeling and reserve calculation uncertainty were selected: fan body boundaries, effective reservoir property thresholds, and variogram range. A full-factor experimental design method was used to design 27 different modeling schemes, ultimately achieving multiple equally probable sand-mud facies geological models. With the static reserve as the goal, the study qualitatively and quantitatively evaluates the significant level of influence of each influencing factor. Through response surface experimental analysis, parameters are optimized, and the best choices for each influencing factor are determined, ultimately constructing the target model for the study area. The main insights gained from this study are as follows:
-
(1)
In response to the reservoir characteristics of the study area with multiple sediment sources, a locally varying variogram was used for unified simulation of the study area, effectively solving the problem of abrupt changes in sand body thickness at partition boundaries. Seismic attributes and sand body thickness maps were comprehensively utilized to delineate pessimistic, possible, and optimistic boundary levels. Under different boundary conditions, the percentages of sand-mud under different effective reservoir property thresholds were statistically analyzed, and the obtained data were applied as conditional constraints in the reservoir modeling process, effectively reducing the uncertainties in reservoir modeling.
-
(2)
Combining the characteristics of the study area and the selection of variograms during the modeling process, the fan body boundary, effective property threshold, and variogram range were analyzed as the main influencing factors in reservoir modeling and reserve calculation. For different influencing factors, optimistic, possible, and pessimistic levels were set, and a full-factor experimental analysis was conducted. The significance and causes of different factors were analyzed, and it was determined that the significant influencing factors for reserve calculation were the effective property threshold and fan body boundary, with the effect of the effective property threshold being more pronounced. The non-significant influencing factor was the variogram range. In response to the actual situation of modeling and the level setting of significant influencing factors, a response surface analysis method was used to analyze the significant influencing factors and reserve results, obtaining a multivariate regression model between reserves and significant influencing factors. A Monte Carlo random simulation method was employed to obtain the cumulative probability reserve distribution, predicting the 3P reserves of the study area.
-
(3)
All kinds of assumptions used in this modeling process, such as boundary conditions and physical property limits, are dependent on the special geological and geophysical data of Yong935-936 block. Therefore, when applying this modeling method to other types of reservoirs, specific analysis and judgment of the corresponding reservoirs are required. Otherwise, it will lead to unnecessary bias, which will affect the result of the final reservoir modeling.
Data availability
Correspondence and requests for materials should be addressed to Pingshan Ma.
References
Li, S. H., Ying, Y. & Zhang, C. M. Series technology of reservoir statistics modeling series technology. (2007).
Jamshidi, E. et al. Scaling-up dynamic elastic logs to pseudo-static elastic moduli of rocks using a wellbore stability analysis approach in the Marun oilfield, SW Iran. Sci. Rep. 14, 19094. https://doi.org/10.1038/s41598-024-69758-w (2024).
Eftekhari, S. H. et al. Electrical facies of the Asmari formation in the Mansouri oilfield, an application of multi-resolution graph-based and artificial neural network clustering methods. Sci. Rep. 14, 5198. https://doi.org/10.1038/s41598-024-55955-0 (2024).
GoovaertsP Geostatistical modeling of the spaces of local, Spatial, and response uncertainty for continuous petrophysical properties. AAPG Comput. Appl. Geol. https://doi.org/10.1306/1063807CA53229 (2006).
Goovaerts, P. & AUTO-IK: A 2D indicator kriging program for the automated non-parametric modeling of local uncertainty in Earth sciences. Comput. Geosci. 35 (6), 1255–1270. https://doi.org/10.1016/j.cageo.2008.08.014 (2009).
Scheidt, C. & Caers, J. R. Spatial uncertainty using distances and kernels. Math. Geosci. 41, 397–419. https://doi.org/10.1007/s11004-008-9186-0 (2009).
Goovaerts, P. Geostatistical modelling of uncertainty in soil science. Geoderma 103 (1), 3–26. https://doi.org/10.1016/S0016-7061(01)00067-2 (2001).
Goovaerts, P. Geostatistical modelling of Spatial uncertainty using P -field simulation with conditional probability fields. Int. J. Geogr. Inf. Sci. 16 (2), 167–178. https://doi.org/10.1080/13658810110099125 (2002).
Loska, K. & Wiechula, D. Application of principal component analysis for the Estimation of source of heavy metal contamination in surface sediments from the Rybnik. Reserv. Chemosphere. 51 (8), 723–733. https://doi.org/10.1016/S0045-6535(03)00187-5 (2003).
Gill, D. Application of a statistical zonation method to reservoir evaluation and digitized-log analysis. AAPG Bull. 54 (5), 719–729. https://doi.org/10.1306/5D25CA35-16C1-11D7-8645000102C1865D (1970).
Araktingi, U. G. & Bashore, W. M. Effects of properties in seismic data on reservoir characterization and consequent fluid-flow predictions when integrated with well logs. SPE24752. 913–926. https://doi.org/10.2118/24752-MS (1992).
Craig Smalley, P., Begg, S. H. & Naylor, M. Handling risk and uncertainty in petroleum exploration and asset management: an overview. AAPG Bull. 92 (10), 1251–1261. https://doi.org/10.1306/06040808063 (2008).
Ma, Y. Z. & Pointe, P. R. La. Uncertainty analysis and reservoir modeling.AAPG https://doi.org/10.1306/m961330 (2011).
Novakovic, D. & Roth, J. Uncertainty analysis in a mature field: Dibi field case study. AAPG Mem. https://doi.org/10.1306/13301411M963481 (2011). 96.121-136.
Park, H., Scheidt, C. & Fenwick, D. History matching and uncertainty quantification of facies models with multiple geological interpretations. Comput. Geosci. 17, 609–621. https://doi.org/10.1007/s10596-013-9343-5 (2013).
Bertolini, A. C., Maschio, C. & Schiozer, D. J. A methodology to evaluate and reduce reservoir uncertainties using multivariate distribution. J. Petrol. Sci. Eng. 128, 1–14. https://doi.org/10.1016/j.petrol.2015.02.003 (2015).
Zhou, L. Q., Xiong, Q. H. & WU, S. H. The principles of selecting and testifying facies models in stochastic modelling. Pet. Explor. Dev. 28 (1), 68–71 (2001).
Liu, W. U. S. H. & Fan, Y. Z. 3D stochastic modeling of sedimentary mic-rofacies with geological and seismic data. J. Palaeogeograph. 5(4): 439–449. https://doi.org/10.7605/gdlxb.2024.06.092(2003).
Venkataraman, R. Application of the method of experimental design to quantify uncertainty. SPE 59422, 1–18. https://doi.org/10.2118/59422-MS( (2000).
Peng, C. Y. & Gupta, R. Experimental design in deterministic modeling: assessing significant uncertainties. SPE 80537, 1–21. https://doi.org/10.2118/80537-MS( (2003).
Moeinikia, F. & Alizadeh, N. Experimental design in reservoir simulation: an integrated solution for uncertainty analysis, a case study. J. Petrol. Explor. Prod. Technol. 17, 75–83. https://doi.org/10.1007/s13202-012-0023-0 (2012).
Huo, C. L., Liu, S. & Gu, L. A quantitative method for appraising reservoir geological model uncertainty. Pet. Explor. Dev. 34 (5), 574–579 (2007).
Sun, L. C., Gao, B. Y. & Li, J. G. A discussion on the methods to study uncertainty of geologic modeling parameters. China Offshore Oil Gas. 21 (01), 35–38 (2009).
Liu, R. M., Luo, Z. & Wang, Z. Application of orthogonal test method in reservoir geological modeling. J. Oil Gas Technol. 32 (04), 208–210 (2010).
Chong, R. J., Yu, X. H. & Li, T. T. Application of experimental design theory in stochastic reservoir model optimization. Oil & Gas Geol. 1 94–100 https://doi.org/10.11743/ogg20120112 (2012).
Xue, Y. X., Liao, X. W. & Zhao, C. M. Uncertainty analysis of fluvial reservoir in oilfield early development period based on stochastic modeling: A case study from A oilfield in Bohai Bay. Lithologic Reservoirs 24 (01) 80–83. https://doi.org/10.3969/j.issn.1673-8926.2012.01.015(2012).
Dong, Y. lnternal heterogeneity analysis of the glutenite reservoir Y227 district in north Dongying sag. (2016).
Qing, F., Yan, J. P. & Wang, J. Division of sedimentary cycle of sandy conglomerate body and its relationship with physical properties: a case study from the upper submember of the fourth member of Shahejie formation in Y920 block of Northern steep slope zone in Dongying Sag. Lithologic Reservoirs. 32 (6), 50–61. https://doi.org/10.12108/yxyqc.20200605 (2020).
Zhang, L. Q. & Yang, W. Multi-provenance depositional model of Paleo gully in North steep slope of Dongying depression of upper Es4inPaleogene. J. Cent. South. University: Sci. Technol. 43 (8), 159–165 (2012).
Meng, Y., Li, Y. Z. & Yang, H. Z. Evolution process and hydrocarbon accumulation significance of Yong1 glutenite body in Es4Member in Yonganzhen oilfield, Dongying Sag. Petroleum Geol. Recovery Effi. 26 (5) 58–65. https://doi.org/10.13673/j.cnki.cn37-1359/te.2019.05.007(2019).
Liu, J. W. Accurate description by well-to-seismic integration of glutenite fine sedimentation in the Northern Dongying Sag, Jiyang sub-basin. Special Oil Gas Reservoirs. 26 (1), 18–25. https://doi.org/10.3969/j.issn.1006-6535.2021.01.003 (2021).
Schlumberger Petrel. Version 2018. Geoscience software. Schlumberger Limited. https://www.slb.com/software/petrel
Author information
Authors and Affiliations
Contributions
Pingshan Ma: Conceptualization of this study, Methodology, Software, Validation, Investigation, Writing-original draft. Chengyan Lin: Conceptualization of this study, Methodology, ReviewHaocheng liu: Review and editing, Supervision. Shaohua Li: Conceptualization of this study, Methodology, Validation, Resources.Shun Wang: Writing, review and editing, Visualization, Supervision.Correspondence and requests for materials should be addressed to Pingshan Ma.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Ma, P., Lin, C., liu, H. et al. Uncertainty evaluation and model optimization in multi-source reservoir modeling. Sci Rep 15, 19004 (2025). https://doi.org/10.1038/s41598-025-04185-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-04185-z