Introduction

In long-distance water conveyance projects, water hammer issues are critical factors affecting pipeline safety. The water hammer phenomenon within pipelines can accelerate pipeline aging and damage, and in severe cases, may lead to pipe bursts or collapses, resulting in water resource waste and threats to public water supply safety1. In China’s northwestern and southwestern regions characterized by complex terrain with significant elevation variations and undulating topography, water transmission projects often feature large elevation differences, multiple undulations, and extended distances. Under such conditions, hydraulic transient processes within water transmission pipelines become particularly complex. When elevated reservoirs supply water to downstream cities through gravity flow systems, lower-lying sections of the pipeline experience higher pressure. During hydraulic transient processes, these pressures may exceed the pipeline’s pressure-bearing capacity2,3.

In water conveyance projects characterized by complex terrain conditions, long distances, and multiple undulations, the significant pressure fluctuations generated by hydraulic transient processes have consistently been a critical factor affecting pipeline safety. On one hand, due to the significant inertia of water flow in long-distance water conveyance pipelines, when valves are gradually closed, the water cannot stop immediately under inertial effects and continues to flow forward for a certain distance. This creates localized high-pressure zones near the valves4, followed by low-pressure zones caused by the rebound of the fluid. These phenomena lead to flow variations and periodic sharp pressure surges and drops in the pipeline, ultimately inducing pipeline vibrations5. On the other hand, in long-distance water conveyance projects with significant elevation differences between upstream and downstream, pipeline elevations fluctuate with terrain variations and may feature multiple raised sections along the route. During hydraulic transients induced by valve closure, negative pressure can create cavitation bubbles, leading to water column separation6. When these cavities collapse, the separated water columns rapidly rejoin and collide, generating intense water hammer effects. This phenomenon produces violent pressure fluctuations that may exceed the pipeline’s designed pressure-bearing capacity, thereby increasing risks of structural damage and operational failures caused by pipeline vibrations7.To mitigate mechanical vibrations caused by pressure fluctuations during hydraulic transient processes. Stosiak8 proposed addressing pressure pulsations that occur during transitional phases of hydraulic systems, such as startup, shutdown, or changes in hydraulic actuator speed or motion direction. His approach involves inserting custom-contoured flexible spacers inside valves and selecting appropriate high-pressure hose materials and structural configurations. These measures aim to mitigate structural vibrations caused by pressure pulsations, thereby ensuring the safe operation of hydraulic systems9,10.

In the pressure fluctuations of long-distance water conveyance pipeline systems, negative pressure merits greater attention than positive pressure11,12, primarily because negative pressure conditions can lead to a series of more severe and challenging issues. When negative pressure occurs within a pipeline, it may induce cavitation under negative pressure, disrupting the continuity of water flow, reducing conveyance efficiency, eroding the inner pipeline walls, and accelerating pipeline aging and damage13,14. If excessive negative pressure develops, the pipeline may undergo deformation or collapse due to external pressure exceeding internal pressure, resulting in severe structural damage15. In contrast, positive pressure issues can generally be effectively controlled through devices such as safety valves and pressure relief valves. However, the aforementioned problems caused by negative pressure are more challenging to resolve, incur greater economic losses, and may pose significant threats to the safe and stable operation of water supply systems. For protection against negative pressure, some scholars have proposed installing air valves at pipeline peaks and one-way surge towers along the pipeline route to mitigate cavitation-induced negative pressure16,17. However, maintaining pipeline pressure within safe limits remains challenging. Most systems integrate one-way surge towers with other protective devices to regulate pipeline negative pressure18. One-way surge towers can effectively provide negative pressure water hammer protection for humped pipelines and also offer negative pressure safeguarding for bidirectional water supply systems19. The number of one-way surge towers required to achieve negative pressure protection has an optimal value, but no specific methodology has yet been proposed to determine this quantity20. Some scholars have begun exploring the optimization and placement of protective devices. They have optimized the design of air vessels in long-distance water conveyance projects and calculated the dimensions of these gas storage units21. Currently, single protective devices are insufficient to meet water hammer protection requirements under long-distance and complex terrain conditions. In long-distance water conveyance projects with complex topography, the optimal solution for water hammer protection involves the combined use of multiple protective devices to regulate pipeline pressure along the entire route. Key technical challenges include selecting the type, quantity, and specifications of these protective devices22,23.

The aforementioned research provides insights and methodologies for safeguarding long-distance water conveyance projects under complex terrain conditions. However, studies on parameter optimization for negative pressure mitigation in unidirectional surge towers under such conditions remain limited. Existing research predominantly focuses on the impact of individual parameters (e.g., surge tower height, tower diameter, or effective depth) on negative pressure control, lacking systematic analysis of the coupling effects of multiple parameters. In practical engineering, complex boundary conditions such as terrain undulations significantly influence parameter optimization outcomes. Nevertheless, current studies often overlook these factors, reducing the engineering applicability of optimized solutions. This study utilizes the method of characteristics to simulate hydraulic transient processes in a long-distance water conveyance project located in Xinjiang, China, characterized by significant terrain fluctuations and numerous pipeline protrusions. Building upon optimal valve closure strategies derived from prior research on this project24, air valves are implemented as fundamental protective devices for water hammer mitigation. Dynamic simulations of the extended pipeline system are conducted using Bentley Hammer software. Subsequently, varying numbers of unidirectional surge towers are incorporated into the protection scheme to assess the impact of multiple factors on negative pressure mitigation. The research establishes a hierarchical prioritization of influencing factors on surge tower performance and validates the protective efficacy under optimal parameter combinations. Finally, the paper summarizes key findings and outlines future research directions. The work aims to establish an optimization framework for protective device parameters in long-distance water transmission pipelines under complex terrain conditions, thereby enhancing operational efficiency and safety of water conveyance systems.

Mathematical methods

Water hammer calculation model

The control equations for pipeline water hammer include the momentum equation and the continuity equation:

momentum equation:

$$L_{1} = \frac{\partial V}{{\partial t}} + V\frac{\partial V}{{\partial x}} + g\frac{\partial H}{{\partial x}} + \frac{fV\left| V \right|}{{2d}} = 0$$
(1)

continuity equation:

$$L_{2} = \frac{{a^{2} }}{g}\frac{\partial V}{{\partial x}} + V\left( {\frac{\alpha H}{{\alpha x}} + \sin a} \right) + \frac{\partial H}{{\partial t}} = 0$$
(2)

In equations of Eqs. (1) and (2), V indicates the flow velocity in the control volume, (m/s); t represents the time variable, (s); g demonstrates the gravitational acceleration, (m/s2); f signifies the Darcy-Weisbach friction factor; H shows the head in the pressure measurement pipe of the control volume, (m) ; x illustrates the distance along the centerline of the pipe(m); d stands for the pipe diameter, (m); ɑ indicates the water hammer wave speed, (m/s); α reveals the pipe slope angle.

The Method of Characteristics (MOC) transforms the governing equations of water hammer into a system of ordinary differential equations along characteristic lines. This approach combines high numerical stability with intuitive physical interpretation, enabling efficient handling of complex boundary conditions and accurate capture of transient pressure waves. It is particularly suitable for modeling and analyzing nonlinear water hammer phenomena in engineering applications. The compatibility equations for pressurized pipelines under the method of characteristics are expressed as follows:

$$C^{ + } :{\text{ }}H_{{Pi}} = C_{P} - BQ_{{Pi}}$$
(3)
$$C^{ - } :H_{{Pi}} = C_{M} + BQ_{{Pi}}$$
(4)
$$B_{p} = \frac{a}{{gA_{c} }} + \frac{f\Delta x}{{2gD_{c} A_{c}^{2} }}\left| {Q_{i - 1} } \right|$$
(5)
$$C_{M} = H_{i + 1} - \frac{a}{{gA_{c} }}Q_{i + 1}$$
(6)
$$B_{M} = \frac{a}{{gA_{c} }} + \frac{f\Delta x}{{2gD_{c} A_{c}^{2} }}\left| {Q_{i + 1} } \right|$$
(7)

In equations Eqs. (3)–(7), HPi and Qpi represent the head and flow rate at section ii at the current time, respectively. CP, CM, BP, and BM are known quantities derived from the flow rates and head measurements of the adjacent sections at the previous time step. a indicates the water hammer wave speed; gg is the gravitational acceleration; Ac illustrates the cross-sectional area of the pipeline; f is the friction factor; Δx shows the segment length; and Dc demonstrates the pipe diameter. Subscripts i + 1 and i − 1 refer to the adjacent sections of point i.

Air valve boundary conditions

This paper utilizes the theory of free gas cavities, assuming that air enters and exits through isentropic valves. Within the pipeline, the air valve adheres to the isothermal law, ensuring that the temperature of both the gas and the liquid remains constant. Consequently, the air that enters the pipeline remains stationary near the air valve. The volume of air is extremely small compared to the volume of the liquid in the pipeline, and the height of the liquid surface within the pipeline essentially remains unchanged25,26,27. Figure 1 illustrates a schematic diagram of the mathematical model of the air valve.

Fig. 1
figure 1

Schematic diagram of the air valve mathematical model.

Full size image

The mass flow rate of air passing through an air valve depends on the absolute pressure P0 and absolute temperature T0 of the outside atmosphere, as well as the absolute pressure P and absolute temperature T inside the pipe. Besides, the intake and exhaust conditions of the air valve can be categorized into the following four situations:

(1) Subsonic flow entering the air(\(0.528p_{0} < p < p_{0}\)):

$$m = C_{in} A_{in} \sqrt {7p_{0} \rho_{0} \left[ {\left( {{p \mathord{\left/ {\vphantom {p {p_{0} }}} \right. \kern-0pt} {p_{0} }}} \right)^{1.4286} - \left( {{p \mathord{\left/ {\vphantom {p {p_{0} }}} \right. \kern-0pt} {p_{0} }}} \right)^{1.7143} } \right]}$$
(8)

(2). (Flow entering the air at critical speed(\({\text{p < }}0.528{\text{p}}_{0}\)):

$$m = C_{in} A_{in} {{0.686} \mathord{\left/ {\vphantom {{0.686} {\sqrt {RT_{0} } }}} \right. \kern-0pt} {\sqrt {RT_{0} } }}p_{0}$$
(9)

(3). (Subsonic flow exiting the air(\({\text{p}}_{0} {\text{ < p < }}\frac{{{\text{p}}_{0} }}{0.528}\)):

$$m = C_{out} A_{out} p\sqrt {\left( {{7 \mathord{\left/ {\vphantom {7 {RT}}} \right. \kern-0pt} {RT}}} \right)\left[ {\left( {{{p_{0} } \mathord{\left/ {\vphantom {{p_{0} } p}} \right. \kern-0pt} p}} \right)^{1.4286} - \left( {{{p_{0} } \mathord{\left/ {\vphantom {{p_{0} } p}} \right. \kern-0pt} p}} \right)^{1.7143} } \right]}$$
(10)

(4). Flow exiting the air at critical speed(\({\text{p > }}{{{\text{p}}_{0} } \mathord{\left/ {\vphantom {{{\text{p}}_{0} } {0.528}}} \right. \kern-0pt} {0.528}}\)):

$$m = C_{out} A_{out} \left( {{{0.686} \mathord{\left/ {\vphantom {{0.686} {\sqrt {RT} }}} \right. \kern-0pt} {\sqrt {RT} }}} \right)p$$
(11)

In Eqs. (10) and (11), m represents the mass flow rate of air entering or exiting, (kg/s); Cin and Cout are the flow coefficients for air entering and exiting; Ain and Aout demonstrate the areas for air entering and exiting, (m2); ρ0 indicates the atmospheric density, (kg/m3); R reveals the gas constant; p shows the absolute pressure in the pipe , (kPa).

When the water pressure inside the pipeline is higher than the atmospheric pressure, the boundary condition of the air valve corresponds to the internal section solution of the conventional characteristic line method. Whereas the water head drops below the pipeline height, air flows in automatically. Before the air is expelled, the gas adheres to the ideal gas law equation.

$$pV = \frac{m}{M}RT$$
(12)

In Eq. (12) involves the molar mass of the gas, denoted as M, (kg/mol).

By integrating the ideal gas Eq. (12), the direction of characteristic lines, and the relationship between pressure and water head, derive the boundary condition equation for the air valve at the final moment of ∆t.

$${\text{P}}\left\{ {{\text{V}}_{{\text{i}}} + 0.5{\text{dt}}\left[ {{\text{Q}}{}_{{\text{i}}} - {\text{Q}}_{{{\text{pxi}}}} \frac{{{\text{C}}_{{\text{P}}} + {\text{C}}_{{\text{M}}} }}{{\text{B}}} + \frac{2}{{\text{B}}}\left( {\frac{{\text{P}}}{\gamma } + {\text{Z}} - \overline{H}} \right)} \right]} \right\} = \left[ {m_{0} + 0.5dt\left( {\dot{m}_{0} + \dot{m}} \right)} \right]RT$$
(13)

Single-direction pressure regulating tower boundary condition

In Fig. 2, a schematic of the one-way pressure regulating tower is revealed. When the system is operating normally, the water level in the regulating tower is below the working pressure of the main pipeline, causing the check valve to close. Consequently, there is no flow between the pressure regulating tower and the pipeline, Qp3 = 0. During the hydraulic transition, the pressure drops, causing Hp < HP3, and the check valve momentarily opens, permitting water from the regulating tower to replenish the main pipeline. According to flow continuity,

$${\text{Q}}_{{{\text{p}}1}} + {\text{Q}}_{{{\text{p}}3}} = {\text{Q}}_{{{\text{p}}2}}$$
(14)
$${\text{Q}}_{{{\text{p}}3}} = {\text{C}}_{{\text{d}}} {\text{A}}_{{\text{p}}} \sqrt {2{\text{g}}\left( {{\text{H}}_{{{\text{p}}3}} - {\text{H}}_{{\text{p}}} } \right)}$$
(15)
Fig. 2
figure 2

Boundary conditions for the one-way pressure regulating tower.

Full size image

Given that the elevation at the bottom of the pressure regulating tower is Z, the water level in the tower at any given moment is:

$${\text{H}}_{{{\text{p}}3}} = {\text{H}}_{3} - {{0.5\Delta {\text{t}}\left( {Q_{p3} + Q_{3} } \right)} \mathord{\left/ {\vphantom {{0.5\Delta {\text{t}}\left( {Q_{p3} + Q_{3} } \right)} {A_{st} }}} \right. \kern-0pt} {A_{st} }}$$
(16)

In Eq. (16), Ast— the diameter of the one-way pressure regulating tower, (m).

By solving the compatibility equations on both sides of the main pipeline, can obtain:

$$\left\{ \begin{gathered} Q_{p1} = {{\left( {C_{p} - H_{p} } \right)} \mathord{\left/ {\vphantom {{\left( {C_{p} - H_{p} } \right)} {B_{1} }}} \right. \kern-0pt} {B_{1} }} \hfill \\ Q_{p2} = {{\left( {H_{p} - C_{m} } \right)} \mathord{\left/ {\vphantom {{\left( {H_{p} - C_{m} } \right)} {B_{2} }}} \right. \kern-0pt} {B_{2} }} \hfill \\ \end{gathered} \right.$$
(17)

From Eqs. (14)–(17), the expression for Qp3 can be derived as:

$$\begin{gathered} Q_{p3} = g\left( {C_{d} A_{p} } \right)^{2} - \left\{ {0.5\left( {B + {{\Delta t} \mathord{\left/ {\vphantom {{\Delta t} {A_{st} }}} \right. \kern-0pt} {A_{st} }}} \right) + \left\{ {0.25\left( {B + {{\Delta t} \mathord{\left/ {\vphantom {{\Delta t} {A_{st} }}} \right. \kern-0pt} {A_{st} }}} \right)^{2} } \right.} \right. \hfill \\ \, \left. {\left. { - \left[ {C_{p} + C_{m} + {{\Delta t} \mathord{\left/ {\vphantom {{\Delta t} {A_{st} Q_{3} - {{2\left( {H_{3} + Z_{T} } \right)} \mathord{\left/ {\vphantom {{2\left( {H_{3} + Z_{T} } \right)} {\left[ {g\left( {C_{d} A_{p} } \right)} \right]^{2} }}} \right. \kern-0pt} {\left[ {g\left( {C_{d} A_{p} } \right)} \right]^{2} }}}}} \right. \kern-0pt} {A_{st} Q_{3} - {{2\left( {H_{3} + Z_{T} } \right)} \mathord{\left/ {\vphantom {{2\left( {H_{3} + Z_{T} } \right)} {\left[ {g\left( {C_{d} A_{p} } \right)} \right]^{2} }}} \right. \kern-0pt} {\left[ {g\left( {C_{d} A_{p} } \right)} \right]^{2} }}}}} \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right\}} \right\} \hfill \\ \end{gathered}$$
(18)

The following system of equations is obtained:

$$\left\{ \begin{gathered} Q_{p1} = \left( {{{C_{p} } \mathord{\left/ {\vphantom {{C_{p} } {B_{1} - {{C_{m} } \mathord{\left/ {\vphantom {{C_{m} } {B_{2} }}} \right. \kern-0pt} {B_{2} }}}}} \right. \kern-0pt} {B_{1} - {{C_{m} } \mathord{\left/ {\vphantom {{C_{m} } {B_{2} }}} \right. \kern-0pt} {B_{2} }}}}} \right) - {{Q_{p3} } \mathord{\left/ {\vphantom {{Q_{p3} } 2}} \right. \kern-0pt} 2} \hfill \\ Q_{p2} = Q_{p1} + Q_{p3} \hfill \\ H_{p} = C_{p} - B_{1} Q_{p1} = C_{m} + B_{2} Q_{p2} \hfill \\ \end{gathered} \right.$$
(19)

Case study

The JK Project, located in a region of Xinjiang, is a long-distance, undulating pressurized gravity-flow water conveyance system. Key pipeline parameters are summarized in Table 1, and an overview of the system is illustrated in Fig. 3. The pipeline spans 94.7 km, starting from Pressure stabilization tank A (water level: 665 m) and terminating at Pressure stabilization tank B (94.7 km mark, water level: 585 m), with a design flow rate of 17.1 m3/s. The pipeline comprises two segments: the 0–64.748 km Sect. (64,748 m in length) uses DN3400 PCCP (Prestressed Concrete Cylinder Pipe), with a calculated water hammer wave speed of 955.33 m/s, while the 64.748–94.7 km Sect. (26,952 m in length) employs DN3200 PCCP, exhibiting a water hammer wave speed of 945.64 m/s. The entire pipeline is buried underground and fully anchored to ensure structural integrity under transient hydraulic conditions. In accordance with the “Technical specifications of prestressed concrete cylinder pipe” (SL 702-2015), PCCP pipes are designed to withstand internal pressures of 2–3 MPa, with a maximum capacity of 5 MPa. For this project, the PCCP pipes adopt a pressure rating of 2.6 MPa, corresponding to a maximum working pressure of 260 m of water column. In compliance with the “Technical specifications of prestressed concrete cylinder pipe” (SL 702-2015), the PCCP pipes adopted in this project are rated for an internal pressure of 2.6 MPa (equivalent to 260 m water column), within their operational capacity of 2–3 MPa (up to 5 MPa maximum). Additionally, adhering to the “Technical specification for long distance water transmission pipeline engineering of urban water supply” (CECS 193-2005), the maximum allowable negative pressure is restricted to -2.0 m (water column), ensuring hydraulic transient safety under complex terrain conditions.

Table 1 Summary of pipeline parameters.
Full size table
Fig. 3
figure 3

JK pressure gravity flow water conveyance project: (a) Schematic diagram of water conveyance system; (b) Schematic diagram and longitudinal section of the water supply pipeline; c Pipeline pressure distribution under normal operating conditions.

Full size image

Results and analysis

Water hammer test and numerical simulation software validation

Current research on transient flow modeling predominantly relies on the rigid water column theory or classical steady-state friction models28.These models typically employ the traditional Method of Characteristics (MOC), which transforms the governing partial differential equations of fluid flow into fundamental finite difference equations, serving as the basis for developing numerical models and computational programs. However, this quasi-steady friction assumption is only valid when wall shear stress remains consistently stable29. To address this limitation, several unsteady friction models have been developed, including a generalized friction model for unsteady Newtonian fluid flow in pipelines30, as well as Weighted Function-Based (WFB) and Instantaneous Acceleration-Based (IAB) unsteady friction models, which overcome the inadequate accuracy of classical steady-state models in predicting pressure oscillation decay31. Consequently, we conducted physical experiments to validate the pressure calculations obtained using the traditional MOC approach under quasi-steady friction assumptions.

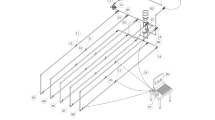
In the hydraulic transient protection design for long-distance water conveyance pipelines, computational modeling and simulation serve as the primary analytical tools. Both Bentley Hammer and KY PIPE software utilize quasi-steady friction models for water hammer pressure calculations. At the Xinjiang Key Laboratory of Hydraulic Engineering Security and Water Disasters Prevention, our research team conducted comprehensive physical valve-closure experiments utilizing an advanced gravity-flow water hammer test platform. Through systematic comparison between the experimentally obtained pressure transient data and numerical simulation results from two industry-standard software packages (Bentley Hammer and KY PIPE), we rigorously evaluated the applicability and limitations of quasi-steady friction models in hydraulic transient analysis. The experimental platform comprises an integrated circulating system combining pump pressurization with gravity-flow water supply. The experimental platform features an integrated circulating system combining both pump-pressurized and gravity-driven water supply configurations. The test platform consists of a water pump pressurization system and a gravity flow water supply system to form a complete circulation system. The gravity flow water supply system uses a 12m3 multifunctional variable head high-pressure water supply system as the water source, and can set the outlet pressure of the air tank. After the system is stabilized, a water hammer test for closing the downstream end valve is carried out. The layout of the test pipeline and equipment are shown in Figs. 4, 5.

Fig. 4
figure 4

Experimental pipeline layout diagram.

Full size image
Fig. 5
figure 5

Water hammer test platform equipment: (a) Multi-functional Variable-head System; (b) terminal valve with upstream/downstream pressure transducers.

Full size image

Using the gravity-flow water hammer test platform, valve-closure experiments were conducted under three different initial pressure conditions at the system inlet: 10, 20, and 30 m. The tests employed an electrically actuated terminal valve with a consistent 30-s closure time (from fully open to fully closed). In long-distance water conveyance projects, computational modeling serves as the primary approach for water hammer protection design and analysis. This study performed numerical simulations of the gravity-flow water hammer phenomena using two distinct methodologies: the quasi-steady friction model implemented in HAMMER software (Method of Characteristics) and KY PIPE software (Wave Characteristic Method). To validate the computational models, simulations were configured with identical 30-s valve closure conditions. The comparative results between numerical predictions and physical experimental data are presented in Fig. 6, demonstrating the effectiveness of both modeling approaches in replicating the transient pressure behavior observed in the experimental system.

Fig. 6
figure 6

Comparison of maximum pressure values at valve inlet.

Full size image

As shown in Fig. 6, under the initial pressure of 10 m, the maximum pressures obtained from physical measurements, HAMMER simulations, and KY PIPE simulations were 15.30, 15.48, and 15.32 m, respectively. The HAMMER and KY PIPE results were 1.16% and 0.13% higher than the measured values, respectively. At an initial pressure of 20 m, the corresponding values were 23.4 m (measured), 25.79 m (HAMMER), and 25.39 m (KY PIPE), with the simulated results exceeding measurements by 9.27 and 7.84%, respectively. For the 30 m initial pressure condition, the recorded values were 33.8 m (measured), 35.98 m (HAMMER), and 35.9 m (KY PIPE), representing over estimations of 6.06 and 5.85%, respectively. The comparative analysis reveals that for both laboratory conditions and numerical simulations of valve-closure-induced water hammer pressures, the computational results exhibit greater deviations from experimental data at higher initial pressures (e.g., 30 m case) compared to lower pressures (e.g., 10 m case). In the laboratory setup, the pipeline was rigidly supported by steel frames and included several connection points equipped with gate valves. At higher initial pressures, significant pipeline vibrations occurred during water hammer events, leading to partial dissipation of pressure wave energy and consequently lower measured values. The maximum discrepancy between simulated and experimental results was 9.27%, with all errors remaining within 10%, demonstrating satisfactory agreement between numerical predictions and physical measurements.

Both Bentley Hammer and KY PIPE software, which adopt the quasi-steady friction model, have the problem of overestimating the measured pressure in their calculations. Among them, the water hammer pressure calculated by Bentley Hammer software is slightly higher than that of KY PIPE software, but the error is controllable and the conservative results meet the safety requirements of engineering. Theoretically, in the time-varying pressure fluctuations at a point on the pipeline, there is little difference in the peak values of the first few segments of fluctuations calculated by the quasi-steady friction and unsteady friction models. That is to say, the difference in the extreme pressure values at a point calculated by different friction models is small, which is consistent with the previous physical test results. The main difference lies in that the pressure wave calculated by the unsteady friction model attenuates more significantly with the prolongation of operation time. However, this study focuses on the extreme pressure along the pipeline and does not pay attention to the change of single-point pressure with time. Considering the physical tests, numerical simulation results and the research focus, Bentley Hammer software with the quasi-steady friction model is therefore used for the water hammer protection calculation of water transmission projects in complex terrains.

Air valve protection

For long-distance and multi-undulating water conveyance projects, the two-stage stepwise valve closing at the end of the pipeline is better than the one-stage linear valve closing. The optimal solution from previous research implemented a two-stage valve closure scheme at the pipeline terminus: 75% closure in 200 s followed by complete (100%) closure in 500 s. However, relying exclusively on phased valve operation strategies and extended closure durations proved inadequate for effectively reducing negative pressure propagation along the pipeline24. Consequently, we augmented this closure strategy with specialized water hammer protection devices to achieve comprehensive transient control. In order to reduce the negative pressure hazard in the pipeline and the water column separation to bridge the water hammer hazard, according to the “Design Specification for Water Hammer Protection of Pressure Flow Pipeline” (DB 65/T 4718-2023), the air valve is used as a basic protective measure in such projects. The larger inlet diameter and the smaller exhaust diameter of the air valve are more effective for the protection of the water hammer. When vaporization occurs in the pipeline and the water flow is interrupted, rapid air intake is required to prevent excessive negative pressure. During water column reclosure, slow exhaust is necessary to prevent the secondary hazards of water hammer caused by flow re-establishment. The three-action air valve has the function of a large amount of air intake when the negative pressure is negative, a large amount of exhaust when the empty pipe is filled with water, and a small amount of exhaust under normal conditions. Therefore, the three-action air valve with high-speed intake and slow exhaust is used for numerical simulation research. Figure 7a displays the pressure envelope along the pipeline under the two-stage valve closure condition. To mitigate negative pressure risks and prevent water column separation-induced water hammer effects, air valves were installed in accordance with the layout principles specified in the Design Specification for “Design Specification for Water Hammer Protection of Pressure Flow Pipeline” (DB 65/T 4718-2023). The air valve deployment strategy included: At the high points of the pipeline, air valves are installed at intervals of 800 m along the long rising sections, 500 m along the long descending sections, and between 500 and 1000 m along the straight sections. This configuration results in a total of 100 air valves distributed along the entire pipeline. For pipeline diameters DN3400/DN3200, the following parameters are selected: inlet diameter D1 = 530/500 mm, large discharge outlet diameter D2 = 110/100 mm, and small discharge outlet diameter D3 = 10/9 mm. Figure 7b illustrates the transient pressure variations along the pipeline equipped with air valves during and after the two-stage valve closure event.

Fig. 7
figure 7

(a) Minimum pressure along pipeline under two–stage valve closing scheme; (b) Pressure envelope along the air valve protection pipeline.

Full size image

Figure 7a shows the minimum pressure envelope along the pipeline under two-stage valve closure. During the preliminary numerical calculations, it was found that for this project, when the valve was closed without any water hammer protection devices installed, the water hammer-induced negative pressure throughout the entire pipeline reached the cavitation pressure of −10 m. The calculated negative pressure value even reached −94.99 m. Such severe negative pressure would cause the entire pipeline to collapse due to suction, leading to the formation of column separation and cavities, posing a serious threat to the project’s safety. In the numerical simulation study, the calculations were performed without considering the effects of water vaporization at −10 m. The pressure values above −10 m represent the actual pressure, while the negative pressure results below −10 m do not reflect the real pipeline pressure but help illustrate the severity of the situation and estimate the variation of water hammer-induced negative pressure in the pipeline. Figure 7b shows that when only the triple-acting air valve is used for protection, the minimum water hammer negative pressure along the pipeline is −13.05 m. Relying solely on the air valve has little effect on the positive water hammer pressure along the pipeline, and the positive pressure along the pipeline meets the protection requirement of 300.5 m. Therefore, for this project, the focus of protection is on mitigating negative pressure. A comparison between Fig. 7b (equipped with air valves) and Fig. 7a (without protective devices) reveals that without air valve protection, the minimum pressure in the pipeline reaches −94.99 m, with severe negative pressure observed throughout the entire pipeline. After implementing air valves for water hammer protection, the negative pressure along the pipeline is significantly alleviated. However, certain sections still exhibit critical negative pressure, with multiple segments registering minimum pressures below −10 m, failing to meet the safety requirements for negative pressure during operation. Air valves demonstrate notable effectiveness in mitigating negative pressure for long-distance water conveyance projects under complex terrain conditions. During valve-closure-induced water hammer, decompression waves propagate along the pipeline, causing rapid pressure reduction. When the pressure drops to a specific threshold, air valves activate to admit air, disrupting the vacuum within the pipeline and reducing negative pressure near their installation points. Nevertheless, their protective efficacy remains limited. Consequently, integrating additional protective measures is essential to ensure comprehensive safety and compliance with operational standards.

Air valve and one-way pressure regulating tower combined protection

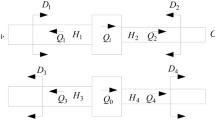
The one-way pressure regulating tower is one of the economical, effective, and reliable protective devices employed to prevent negative pressure and reduce excessive pressure surges induced by water hammers. By combining the one-way pressure regulating tower with the existing air valves, the water hammer protection analysis for the project is further enhanced. The specified parameters for the one-way pressure regulating tower are an outlet diameter of 500 mm, a tower diameter of 5 m, and an effective water depth of 6 m. Four distinct installation schemes and specific installation locations for the one-way pressure regulating tower are indicated in Fig. 8.

Fig. 8
figure 8

Four different installation schemes for the one-way pressure regulating tower.

Full size image

Preliminary calculation analysis with distinct numbers of one-way pressure regulating towers. Preliminary calculations were conducted by adding various numbers of one-way pressure regulating towers. Numerical simulation software was adopted to analyze the water hammer for varying quantities of one-way pressure regulating towers and quantify the negative water hammer pressure after protection. Initially, 1 to 4 appropriate numbers of pressure regulating towers were selected. Hydraulic transient process calculations were performed for protection schemes with divergent numbers of one-way pressure regulating towers, resulting in the pipeline pressure envelope along the route indicated in Fig. 9a, and the extreme pressure values for each scheme are revealed in Fig. 9b. As illustrated in Fig. 9b, after setting distinct numbers of one-way pressure regulating towers, there was no substantial fluctuation in the maximum water hammer pressure envelope along the pipeline, while the minimum negative pressure consistently improved. The results for different numbers of one-way pressure regulating towers are illustrated in Table 2. From Table 2, it is clear that changing the number and ___location of one-way pressure regulating towers did not significantly affect the maximum pressure value improvement, indicating that one-way pressure regulating towers are not effective in protecting against positive water hammer pressure in the pipeline. Additionally, after setting different numbers of one-way pressure regulating towers, the maximum water hammer pressure envelope along the pipeline shows no significant fluctuation, and the minimum negative pressure along the pipeline rises continuously from −11.32 to −7.46 m. As the number of one-way pressure regulating towers increased from 1 to 4, the improvements in negative pressure along the pipeline were 13.26, 10.60, 9.78, and 18.29%, respectively. Besides, the negative pressure improvement values were all below 18.29%. On one hand, brief instances of negative pressure in the pipeline created cavities, prompting the one-way pressure regulating towers to rapidly inject water, thereby generating a pressure wave. With the increase in the number of one-way pressure regulating towers, complex pressure wave superpositions and fluctuations occurred, leading to minimal improvement in the pipeline’s minimum pressure. On the other contrary, the additional one-way pressure regulating towers had lower elevations, and the phenomenon of liquid column separation was not significant, diminishing their effectiveness in controlling pressure increases caused by water hammer pressure waves, resulting in minimal improvement in the minimum pressure. When distinct numbers of one-way pressure regulating towers were set along the pipeline, with 4 one-way pressure regulating towers, the minimum pressure value was −7.46 m, with a maximum increase of 18.29%. The minimal pressure improvement was not significant, indicating that varying the number of one-way pressure regulating towers along the pipeline has a limited protective effect. Simply increasing the number of one-way pressure regulating towers to enhance negative pressure could result in higher project costs.

Fig. 9
figure 9

(a) Pipeline pressure envelope along the length; (b) Pressure extremes under different scenarios.

Full size image
Table 2 Protective effects of different numbers of one-way pressure regulating towers.
Full size table

Since the protective effect of one-way pressure regulating towers depends on the outlet diameter, tower diameter, and effective water depth, further investigation is required to assess whether optimizing these parameters can effectively control the pipeline water hammer pressure in this water conveyance project.

Optimization of one-way pressure regulating tower parameters

In long-distance water conveyance projects, merely increasing the number of one-way pressure regulating towers after basic air valve protection has limited effect on controlling the minimum negative pressure along the pipeline. Since the protective effect of one-way pressure regulating towers is influenced by the outlet diameter, tower diameter, and effective water depth, this section focuses on examining how these three parameters—outlet diameter, tower diameter, and effective water depth—affect water hammer protection. To determine reasonable parameters for the one-way pressure regulating towers, simulation results meet the requirements of the “Pump Station Design Code” (GB50265-2022) on the condition that the outlet diameter is 500 mm, the tower diameter is 5 m, and the effective water depth is 6 m. Besides, the optimal parameters still need further investigation. The range of outlet diameters for the one-way pressure regulating towers is 300 mm to 900 mm; the tower diameter range is 2 m to 8 m, and the effective water depth range is 2 m to 8 m. A three-factor, four-level orthogonal experiment is set up, with experimental factors and levels as indicated in Table 3.

Table 3 Factors and levels design.
Full size table

An L16(43) orthogonal experiment table with 3 factors and 4 levels was automatically generated adopting SPSS.27, resulting in 16 experimental schemes. Besides, the corresponding water hammer pressures for each scheme are illustrated in Table 4.

Table 4 L16(43) Orthogonal experimental schemes and water hammer pressure calculation results.
Full size table

Analysis of the orthogonal test results in Table 4 indicates that all three factors in the single-direction pressure regulation tower significantly impact water hammer negative pressure. To assess the impact of these three factors on the extreme values of pipeline water hammer negative pressure, response surface, and contour plots of the minimum negative pressure were generated, as illustrated in Fig. 10. The three response surface plots in Fig. 10 reveal that the response surfaces are pronounced, indicating that there is no linear correlation between effective depth, tower diameter, outlet diameter, and minimum negative pressure. Additionally, the variation in minimum negative pressure resulting from changes in one factor while another factor changes is significant, implying that interactions exist between effective depth, tower diameter, and outlet diameter affecting the minimum negative pressure. From Fig. 10a, it is evident that on the condition that effective depth is constant, the tower diameter factor plays a dominant role. Increasing either the diameter of the tower body or the outlet diameter can improve the minimum negative pressure in the pipeline. Nonetheless, when the tower diameter is small, the effect of increasing the outlet diameter alone on enhancing the minimum negative pressure is not significant. On the condition that the tower diameter reaches a certain value, increasing the outlet diameter can result in adverse conditions where the negative pressure decreases, illustrating that increasing the outlet diameter to improve the pipeline’s minimum negative pressure has limitations. From Fig. 10b, it is observed that, with a constant outlet diameter, increasing the effective depth generally enhances the pipeline’s minimum negative pressure, although a decrease in negative pressure may still occur. Conversely, when the effective depth is small, enlarging the outlet diameter can improve the negative pressure. However, when the effective depth exceeds 4 m, increasing the outlet diameter can worsen the pipeline’s minimum negative pressure. Moreover, increasing both the effective depth and outlet diameter may still result in a decrease in minimum negative pressure. From Fig. 10c, it is evident that for the two parameters of effective depth and tower diameter, the tower diameter dominates. When the diameter of the tower body is small, merely increasing the effective depth is inadequate to enhance negative pressure. At a constant tower diameter, increasing the effective depth has minimal impact on the pipeline’s minimum negative pressure and may even lead to a decrease in minimum negative pressure. Meanwhile, increasing both effective depth and tower diameter results in a noticeable increase in the gaps between lines, substantially improving negative pressure. It is advised that, when the effective depth is small and the outlet diameter is fixed, increasing the tower diameter can fulfill the additional water requirements needed to generate negative pressure and cavitation in the main pipeline, thereby preventing the depletion of water in the tower. The increase in tower diameter further increases the weight of the water in the tower. Meanwhile, the water in the tower relies on gravity to supplement the pipeline. If this gravitational pressure is inadequate, the water supply from the tower to the main pipeline will be slow, making it challenging to effectively disrupt the water column separation. Consequently, increasing the tower diameter can effectively enhance the minimum negative pressure in the pipeline.

Fig. 10
figure 10

Contour plot of the response surface factors for minimum negative pressure: (a) Calculation condition 1; (b) Calculation condition 2; (c) Calculation condition 3.

Full size image

From Table 4, it is obvious that the minimum water hammer negative pressure can be controlled within −3 m. For the purpose of analyzing the extent of each factor’s impact on suppressing the pipeline’s minimum water hammer negative pressure in the single-direction pressure regulation tower, a range analysis of the schemes designed in Table 4 was performed. The results are indicated in Table 5, where the k value illustrated the average minimum negative pressure at various levels of a factor. The range value R = max(k)−min(k) indicates the extent of the factor’s influence on the minimum negative pressure, a larger R value indicates a greater influence of the factor on the minimum negative pressure.

Table 5 Range analysis of minimum negative pressure.
Full size table

From the k values in Table 5, it is apparent that as the outlet diameter (A) increases, the minimum negative pressure first increases and then remains constant. As the tower diameter (B) increases, the minimum negative pressure demonstrates a progressively increasing trend with a relatively significant increment. As the effective depth (C) increases, the minimum negative pressure also shows an increasing trend, and yet with a smaller increment. Based on the R values, the impact of factors on the negative pressure protection effect of the single-direction pressure regulation tower, in descending order, is: tower diameter (B), outlet diameter (A), and effective depth (C), which is consistent with the response surface analysis. For this project, the optimal parameter combination is A3-B4-C4.

Verification of water hammer protection scheme

Based on the previous results, the optimal parameter combination scheme of pipeline water hammer protection is verified. For the pipeline’s minimum negative pressure, the best parameter combination is A3-B4-C4. Under this configuration, the outlet diameter of the one-way pressure regulating tower is 700 mm, the tower diameter is 8 m, and the effective water depth is 8 m. Calculations for this optimal scheme show the pipeline water hammer pressure envelope as illustrated in Fig. 11.

Fig. 11
figure 11

Pipeline water hammer pressure envelope under optimized scheme.

Full size image

Figure 11 displays the water hammer pressure envelope of the pipeline under the optimized scheme. After implementing the unidirectional surge tank protection, the extreme water hammer pressures are significantly improved. The maximum positive pressure is 246.43 m, occurring at 71.580 km of the pipeline, while the minimum negative pressure is −1.89 m, observed at 83.570, 83.730, 86.120, and 86.400 km. Compared to the air valve-only protection scheme shown in Fig. 7b, the optimized surge tank approach maintains the same maximum positive pressure but slightly reduces it in the front section of the pipeline. The minimum negative pressure increases from −13.05 to −1.89 m, representing an 83.75% improvement. Additionally, without the surge tank, multiple nodes along the pipeline exhibit varying degrees of negative pressure, with several locations reaching vaporization pressure. After surge tank implementation, all negative pressures are elevated above the vaporization threshold, demonstrating that the surge tank not only reduces peak negative pressure but also optimizes the overall negative pressure distribution. These results indicate that the synergistic interaction between surge tanks and air valves in a combined protection system significantly enhances hydraulic transient mitigation effectiveness in water conveyance systems.

Discussions

In this paper, the traditional mindset of single water hammer protection by adding different devices to control pipeline pressure is changed, and the optimized design of water hammer equipment parameters is proposed. The research results are applicable to the water hammer protection design of long-distance gravity flow water transmission projects under complex topographic conditions, especially in scenarios with significant topographic undulations, multiple convex pipe sections, and high negative pressure protection requirements. However, this study still has the following limitations: First, the pipeline structural vibration induced by water hammer pressure fluctuations is not considered, especially in the sudden height difference section, the sudden pressure change may excite pipeline resonance, and the risk of fatigue damage to the pipeline structure caused by dynamic loads is ignored; Second, the collaborative regulation of positive and negative pressure has not been carried out. Although the positive pressure meets the requirements, it has not been further optimized, which may miss the space for improving the overall protection efficiency; Third, the layout of protection equipment has not been optimized. The positions of one-way surge tanks and air valves are fixed, and the influence of spatial layout on pressure wave superposition has not been explored. Finally, the numerical model does not integrate the non-steady-state friction effect, and the quasi-steady-state friction assumption may weaken the accuracy of the transient attenuation process in the low-pressure area.

Future research can be deepened in multiple dimensions: First, conduct in-depth studies on pipeline structural vibration and fatigue damage by introducing fluid–structure interaction models to analyze the interaction mechanism between water hammer pressure fluctuations and pipeline structural vibration, quantify the impact of dynamic loads in sudden height difference sections on the pipeline’s fatigue life, and establish criteria for the selection and layout of protective equipment based on vibration responses, thereby enhancing the structural safety of the water transmission system. Second, optimize the positive–negative pressure collaborative regulation mechanism by integrating devices such as safety valves and pressure reducing valves on the basis of existing negative pressure protection to construct a joint positive–negative pressure regulation model, and use multi-objective optimization algorithms (such as genetic algorithms) to simultaneously optimize the extreme values of positive and negative pressures, achieving an overall improvement in the protection efficiency of hydraulic transient processes. Third, optimize the spatial layout of protective equipment by breaking away from the fixed-position assumption, applying dynamic programming or particle swarm algorithms to explore the optimal spatial arrangement of one-way surge tanks and air valves, analyzing the influence of different positions on the propagation and superposition of pressure waves, and developing an intelligent optimization method for equipment layout based on topographic features. Finally, integrate non-steady-state friction effect models by introducing unsteady friction models to correct the limitations of quasi-steady-state friction assumptions, improving the simulation accuracy of pressure wave attenuation in low-pressure areas and providing more reliable theoretical support for predicting water hammer pressures in complex terrains.

Conclusion

This study investigates the effectiveness of single-direction pressure regulating towers for water hammer protection in a long-distance, multi-elevation gravity flow water conveyance project through numerical simulations, with a focus on optimizing the internal structural parameters of the towers. The results are as follows:

  1. (1)

    For gravity flow water transmission projects in long-distance and multi-undulating complex topographic conditions, increasing the number of protective devices of the same type has no significant impact on the extreme pressure along the pipeline, and joint protection by appropriate devices is required. Increasing the number of one-way surge tanks has little effect on positive pressure protection. Meanwhile, the maximum increase in the minimum negative pressure of this project is only 18.29%, and the minimum negative pressure value is −7.46 m, which is far from meeting safety requirements. Continuously increasing the number of one-way surge tanks to control the extreme pressure along the pipeline obviously does not meet the requirements of engineering economy.

  2. (2)

    The interactive effects of the outlet diameter of the one-way surge tank, tank body diameter, and effective depth influence the minimum negative pressure in the pipeline. The order of influence of each factor on negative pressure is as follows: tower diameter > outlet diameter > effective depth. The tank body diameter plays a dominant role in negative pressure protection. Increasing the tank body diameter can prolong the duration of water replenishment to the pipeline, stabilize pipeline pressure, and avoid tank emptying failure.

  3. (3)

    For long-distance water conveyance projects in complex terrain, the quantity of similar protective devices can be determined based on the pressure improvement magnitude. The structural parameters of the protective devices should also be optimized to attain the maximum protective effect. In this project, the number of one-way surge tanks exhibits a non-linear relationship with the pressure improvement amplitude, with the maximum negative pressure improvement reaching 18.29%. On this basis, compared with that before parameter optimization, the minimum negative pressure has been increased by 83.75%, significantly enhancing the negative pressure protection effect along the pipeline.

This study enhances the understanding of negative pressure protection of gravity flow water supply system under complex terrain with many ups and downs, long distances and large elevation differences, and provides technical guidance for the design of protection scheme of one-way surge tower and the parameter selection of protection equipment, in order to improve the water hammer protection system of gravity flow long-distance water supply project under complex terrain conditions with efficient pressure control and reasonable engineering economy.