Introduction

In recent years, the theory of nonlinear and complex adaptive systems has developed rapidly1. Various research teams and departments have developed combat simulation systems based on this theory, which better reflect the characteristics of nonlinearity and complexity among individuals in combat. This has opened new avenues for research in modern combat simulation. Compared to general simulation training systems, large-scale simulation systems require significantly higher standards of data accuracy and reliability. The quality of the data directly impacts the series of applications or decision-making processes based on simulation results. An inaccurate simulation outcome could lead to critical decision-making errors2. To a certain extent, ensuring the quality of the data used in simulations is a prerequisite for the credibility of large-scale simulation systems. Only with high-quality data can the simulation results possess practical value, and the large-scale simulation system itself demonstrate its vitality. Given the inherent complexity of military operations or related issues, data quality becomes a particularly critical factor in large-scale military simulation systems. While the importance of model verification, validation, and accreditation (VV&A) has been gradually recognized, research on methods for assessing and improving the quality of data used in these simulations remains limited. With the advent of the information age, the quantity of data has increased exponentially, making it challenging to ensure data quality; thus, the assessment of data quality has become increasingly important3. Combat data, as an input component of combat simulation systems, significantly affects the correctness and rationality of the output results. Currently, there is no universally accepted definition of data quality. The U.S. National Information System Dictionary defines data quality as “the degree to which data is suitable for user application, including attributes such as accuracy, timeliness, precision, completeness, relevance, and expressiveness”. The quality of simulation data is influenced and constrained by a variety of factors, making it necessary to quantify these factors when evaluating data quality4. A data quality evaluation index system refers to a set of interrelated metrics designed to achieve a specific research objective. Its establishment not only requires identifying which influencing factors constitute the evaluation system but also determining the relationships among these metrics, i.e., the structure of the index system. The primary goal of evaluating data quality in a simulation system is to comprehensively understand the overall state of data quality. Therefore, it is essential to assess the quality of combat data. In contemporary modern warfare, a plethora of combat data emerges, with useful and useless data intermixed, leading to challenges in ensuring quality. A scientific and rational assessment of this data can enhance combat planning and improve the decision-making capabilities of commanders5. Additionally, the evaluation of combat data quality plays a crucial role in refining operational plans and optimizing command decisions.

Currently, many research outcomes have emerged regarding the assessment of combat data quality. In combat data quality evaluation, hierarchical analysis methods are commonly used to establish a certain hierarchical structure. Within such structures, determining the weights of various indicators related to combat data quality is particularly crucial. The primary methods for calculating indicator weights include the following:

  1. (1)

    Subjective weighting methods.

Common subjective weighting methods include FAHP6, expert survey methods7, G1 method8, and ratio comparison scoring methods9. Among these, FAHP and expert surveys are the two most commonly used methods, which are detailed below.

FAHP: FAHP is one of the commonly used subjective weighting methods. It is developed from the Analytic Hierarchy Process (AHP)10 and serves as a hierarchical weight decision analysis method11. In FAHP, fuzzy sets replace the data in the judgment matrix of AHP, allowing for the calculation of fuzzy weights for each element. The core idea is to quantitatively handle qualitative issues and to structure problems hierarchically. FAHP requires the establishment of a hierarchical system for the attributes, where upper-level attributes influence lower-level attributes. However, FAHP has its limitations; if the hierarchy is constructed improperly or the weight values are set inappropriately, it can adversely affect the final decision outcome.

Expert Survey Method: Also known as the Delphi method, proposed by Gordon and Helmer, this method aims to avoid the tendency for individuals to blindly follow the majority or yield to authority. In the expert survey method, experts assess various proposed indicators and determine their respective weight values. Throughout the process, the experts do not communicate with each other and independently provide their opinions. The results are then aggregated to derive a final conclusion. However, this method is complex and time-consuming, resulting in poor real-time applicability.

  1. (2)

    Objective weighting methods.

In subjective weighting methods, weight values are derived from the experts’ experiences, lacking a data-driven formula, which affects objectivity. Objective weighting methods address this issue. Currently, objective weighting methods mainly include the entropy method12, principal component analysis13, maximum deviation method (MDM)14, and multi-objective programming15, among others. Among these, the entropy method and maximum deviation method are the two most commonly used. The reliability of weights obtained through objective weighting methods is generally higher, as they are based on actual decision data and utilize mathematical methods to construct weighting formulas, allowing for the determination of weight values through these formulas16.

In the study of data quality assessment methods, in addition to subjective and objective weighting methods, many researchers have proposed various alternative approaches. For instance, Liu L J17 constructed a six-tuple evaluation model that combines rough set theory with BP neural network theory for assessing the quality of combat data. He W H18 proposed a comprehensive data quality assessment model that integrates supervised pattern recognition with BP neural networks. This assessment method enhances the accuracy of data evaluation and reduces errors; however, it requires a large volume of data, and when the dataset is small, the evaluation results can be significantly compromised. Yang H19 et al. and colleagues built a three-layer combat data quality indicator assessment model to evaluate the quality of combat data. This model has lower data requirements but is heavily influenced by subjective factors, leading to considerable errors in the results. Han Z J20 et al. proposed a data quality assessment method for large-scale simulation systems that combines both subjective and objective approaches for evaluating combat data quality. This method reduces the influence of subjective factors, but it lacks the definition of thresholds, making it difficult to effectively mitigate the impact of indicator values, resulting in inaccuracies in the evaluation outcomes. Qiu S21 et al. proposed a data valuation evaluation method based on analytic hierarchy process, which improved the accuracy of data evaluation. On the foreign side, Irvanizam et al.22,23 adopted a multi-criteria decision-making method to conduct quality assessments in health care services and social assistance. Yu G F et al.24,25 established a multi-objective decision-making level evaluation optimization model to evaluate the network security situation. However, the attribute information considered by the proposed method is single.

In response to this, and based on relevant literature, this study proposes a combat data quality assessment method using a double-weighted approach based on FAHP optimized by CVF. The structure of this paper is organized as follows. "Fuzzy analytic hierarchy process" Section discusses the theory of FAHP and the method of calculating the weight formula of fuzzy complementary judgment matrix. "FAHP-CVF combat data quality assessment method based on index double weighted" Section identifies key influencing factors and constructs a new combat data quality evaluation index system, and proposes an FAHP optimized by CVF combat data quality evaluation method based on double-weighted of indicators. The thresholds for each indicator are established, and consistency satisfaction optimization is applied to the FAHP-derived weights to obtain the first layer of weights. CVF is then constructed to generate the second layer of weights. The double-weighted evaluation theory is proposed to integrate the first and second layers of weights. "Experimental results and discussion" Section evaluates combat data quality and Pearson correlation coefficient, Spearman correlation coefficient, significance and difference index were used to analyze the results obtained by the four methods. Lastly, "Conclusion"Sect. presents some conclusions of the study.

Fuzzy analytic hierarchy process

FAHP is a research method that combines fuzzy mathematics with the Analytic Hierarchy Process26,27. This method is widely used in the field of determining indicator weights and improves the issues present in traditional Analytic Hierarchy Process, significantly enhancing the reliability of decision-making. The basic idea of FAHP is to decompose the problem into a multi-level structure based on the nature of the evaluation problem28,29. When solving the problem, it mainly involves three steps:

  • Establishing a multi-level model and conducting a reasonable analysis of the causal relationships between factors within each level.

  • Comparing pairwise the factors within the same level based on the criteria of the previous level to determine their relative importance and construct a fuzzy judgment matrix.

  • After calculation, rationalize the ranking of the required alternatives based on the relative importance of each factor, thus providing a rational and scientific decision-making basis for the final decision.

    1. A.

      Establishment of fuzzy complementary judgment matrix.

In the fuzzy analytic hierarchy process, when pairwise comparisons are required among indicators, a quantitative representation of the relative importance of one factor to another is used, resulting in a fuzzy judgment matrix \(A={({a_{ij}})_{n \times n}}\). It has the following properties:

  • \({a_{ii}}=0.5,i=1,2, \cdots ,n\);

  • \({a_{ij}}+{a_{ji}}=1,i,j=1,2, \cdots ,n\);

This type of judgment matrix is called a fuzzy complementary judgment matrix30. To facilitate the quantitative description of the relative importance of any two indicators with respect to certain criteria, a 0.1 to 0.9 scale method, as shown in Table 1, is adopted to scale the quantities.

Table 1 0.1–0.9 scaling method and its significance.
Full size table

According to the above digital index scale, the fuzzy complementary judgment matrix of Formula (1) can be obtained by comparing the index factor \({a_1},{a_2}, \cdots ,{a_n}\) in pairs.

$$A=\left[ {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}&{\ldots}&{{a_{1n}}} \\ {{a_{21}}}&{{a_{22}}}&{\ldots}&{{a_{2n}}} \\ {\ldots}&{\ldots}&{\ldots}&{\ldots} \\ {{a_{n1}}}&{{a_{n2}}}&{\ldots}&{{a_{nn}}} \end{array}} \right]$$
(1)
  1. B.

    Weight formula of fuzzy complementary judgment matrix.

According to the fuzzy complementary judgment matrix, formula (2) can be used to solve the weight of the fuzzy complementary judgment matrix31. The weight formula is as follows:

$${W_i}=\frac{{\sum\limits_{j}^{n} {{a_{ij}}+\frac{n}{2} - 1} }}{{n(n - 1)}},(i=1,2, \cdot \cdot \cdot ,n)$$
(2)

FAHP-CVF combat data quality assessment method based on index double weighted

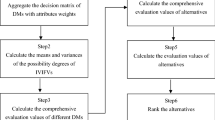
The flow chart of combat data quality assessment method based on index double-weighted is shown in Fig. 1.

Fig. 1
figure 1

Flow chart of combat data quality assessment method based on double-weighted.

Full size image
  1. A.

    Establish combat data quality index system.

Since combat data is derived from the effective integration of operational data across different systems, it is essential that each subsystem adheres to specific evaluation criteria during data storage, transmission, and integration processes to establish a unified standard. This is followed by data cleansing to eliminate irrelevant or faulty data, thereby ensuring the effectiveness and reliability of combat data. The quality of combat data primarily consists of inherent attributes and intrinsic indicators. For the overall assessment of combat data quality, a hierarchical decomposition method is employed, categorizing combat data into three broad types: inherent attributes, expressive attributes, and application attributes. These attributes represent the primary indicators within the combat data quality assessment framework. Specifically, inherent attributes include three secondary indicators: completeness, accuracy, and uniqueness; expressive attributes encompass consistency, timeliness, and understandability; application attributes consist of security, compliance, and stability.

After establishing the combat data quality indicator assessment framework, each indicator is quantitatively processed, allowing all indicators within the framework to be represented by numerical values, referred to as indicator values. The overall structure diagram of the combat data quality indicator system influenced by these indicators is illustrated in Fig. 2.

Fig. 2
figure 2

Quality index system of combat data.

Full size image

In the evaluation study, the threshold indicators are determined by combining the threshold values proposed in reference17 with the standards that each indicator must meet within the project. Each indicator corresponds to a specific threshold, which is established to assess whether the indicator values meet the minimum standards. The basis for setting these thresholds includes: ① the researcher’s emphasis on specific combat data; ② the reliability of the system being evaluated; ③the effectiveness of the researchers in analyzing combat data using the dataset; ④ the experience from previous analyses of combat data and conclusions drawn from simulation experiments. The various threshold indicators used are presented in Table 2.

Table 2 Indicator threshold table.
Full size table

The threshold value corresponding to \(\:{\text{Z}}_{\text{i}}\) represents the lowest standard score that this index should achieve. \(\:{\text{Z}}_{1}\) for completeness, \(\:{\text{Z}}_{2}\) for accuracy, \(\:{\text{Z}}_{3}\) for uniqueness, \(\:{\text{Z}}_{4}\) for consistency, \(\:{\text{Z}}_{5}\) for timeliness, \(\:{\text{Z}}_{6}\) for understandability, \(\:{\text{Z}}_{7}\) for security, \(\:{\text{Z}}_{8}\) for compliance, and \(\:{\text{Z}}_{9}\) for stability.

  1. B.

    Fuzzy consistent compatibility test.

The weight values obtained from Formula (2) are based on the evaluation results of individual experts and are susceptible to personal subjective factors, resulting in inaccurate final evaluation results. Therefore, it is necessary to summarize and analyze the evaluations of multiple experts to obtain a reasonable evaluation result and eliminate unreasonable evaluation results. Therefore, the method of data fuzzy consistency32 and compatibility33 is used to test the evaluation results.

When \(A={({a_{ij}})_{n \times n}}\) and \(B={({{\text{b}}_{ij}})_{n \times n}}\) are both fuzzy judgment matrices, formula (3) is used to solve the compatibility index of matrices A and B between them. The formula is shown below:

$$I(A,B) = \frac{1}{{{n^2}}}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {|{a_{ij}} + {b_{ij}} - 1|} }$$
(3)

\(W={({W_1},{W_2}, \cdot \cdot \cdot {W_{\text{n}}})^T}\) is used to represent the weight vector of fuzzy judgment matrix \(\:\text{A}\), and \(\sum\limits_{{i=1}}^{{\text{n}}} {{W_i}=1,{W_i} \geqslant 0(i=1,2, \cdot \cdot \cdot ,n)}\), let \({W_{{\text{ij}}}}=\frac{{{W_i}}}{{{W_i}+{W_j}}},(\forall i,j=1,2,3, \cdot \cdot \cdot ,n)\), then the characteristic matrix of judgment matrix A is:

$${W^*} = {({W_{ij}})_{n*n}}$$
(4)

To verify the accuracy of the obtained fuzzy complementary judgment matrix, consistency, and compatibility tests are required, which are:

  • When \(I(A,{W^*}) \leqslant \alpha\) is used, it can be shown that the judgment matrix A satisfies satisfactory consistency.

  • When \(I(A,B) \leqslant \alpha\) is used, it can be shown that both the judgment matrices A and B satisfy satisfactory compatibility.

Here, α represents the attitude of the decision maker. The smaller the value of α, the higher the requirement for consistency and compatibility of the decision maker for this fuzzy judgment matrix, and α is usually taken as 0.1.

When both conditions (1) and (2) are satisfied at the same time, the average of the \({\rm{m}}(m \le n)\) weight sets that satisfy the conditions can be used as the weight allocation vector for the factor indicators, and the weight vector expression is as follows, where, Wi represents the final weight vector of the first weight.

$${W_i} = \frac{1}{n}\sum\limits_1^m {{W_i}(i = 1,2, \ldots ,n)}$$
(5)
  1. C.

    Construction of comparison value function.

The comparison function is used to compare the indicator value and threshold, and the comparison value between the indicator value and threshold can be obtained through calculation to control the growth rate of the final weight. The formula for constructing the comparison function \({{\rm{g}}_i}\) is as follows, where xi represents the index value of i indicators, ui represents the threshold value of i indicators, s is the adjustment of the growth rate of the comparison value function, t is used to control the maximum value of gi when the comparison value is greater than the threshold value, and the evaluation result can be closer to the standard value by adjusting s and t.

$${{\text{g}}_i}=\left\{ \begin{gathered} 1/{e^{|{x_i} - {{\text{u}}_i}{|^s}}},{x_i}<{u_i} \hfill \\ 1,({x_i}={u_i}) \cap (({x_i}>{u_i})and \cup ((t - 1/{e^{|{x_i} - {u_i}{|^s}}})<0) \hfill \\ 1+(t - 1/{e^{|{x_i} - {u_i}{|^s}}}),and({x_i}>{{\text{u}}_i}) \cup (t - 1/{e^{|{x_i} - {u_i}{|^s}}}) \geqslant 0 \hfill \\ \end{gathered} \right\}$$
(6)

This formula is derived based on the characteristics of the Sigmoid function and piecewise function. It represents the following meaning:

  • When the indicator value is smaller than the threshold, the larger the difference between them, the smaller the comparison value, which tends to 0; conversely, when the difference is smaller, the comparison value is larger and tends to 1.

  • When the indicator value is equal to the threshold or greater than the threshold and the difference between them is small, the comparison value is 1.

  • When the indicator value is greater than the threshold, the larger the difference between them, the larger the comparison value, which is greater than 1; and when the difference is smaller, the comparison value tends to 1.

Figure 3 is the formula curve when s = 1/4 and t = 0.5 in formula (6).

Fig. 3
figure 3

Comparison value function curve when s = 1/4 and t = 0.5.

Full size image

In Fig. 3, the abscissa is the value of \(({x_i} - {u_i})\), indicating the difference between the index value and the threshold, and the ordinate is \({g_i}\), indicating the comparison value. It can be seen from Fig. 3 that the function curve conforms to the three criteria for constructing the comparison value function.

  1. D.

    Double weighted assessment method.

Using formula (7), the final result value G is evaluated by combining the indicator values, weights, and comparison values, with the combat data quality evaluation results as the result value. Where W2i represents the first weight vector of the secondary sub-indicator Zi, which is obtained through the idea of weight determination using fuzzy analytic hierarchy process by pairwise comparison of indicators and subsequent consistency and compatibility analysis. gi represents the second weight of the secondary sub-indicator Zi, which is obtained by comparing the indicator value with the threshold value to obtain a comparison value. When the indicator value is lower than the threshold value, it indicates that it is lower than the minimum standard, and the corresponding second weight will decrease. Conversely, when the indicator value is greater than the threshold value, indicating that it is higher than the minimum standard, the second weight will increase. xi represents the indicator values corresponding to each indicator Zi. W11, W12, W13 represents the weights corresponding to the inherent attributes, expressive attributes, and application attributes of the primary sub-indicator.

$$G = (\sum\limits_{i = 1}^3 {{W_{2i}}{g_i}{x_i}} ){W_{11}} + (\sum\limits_{i = 4}^6 {{W_{2i}}{g_i}{x_i}} ){W_{12}} + (\sum\limits_{i = 7}^9 {{W_{2i}}{g_i}{x_i}} ){W_{13}}$$
(7)

Experimental results and discussion

  1. E.

    Test data and experimental design.

In the course of actual combat simulation, a lot of combat data will be generated. The different weights of each index that affect the quality of combat data lead to different index scores. The hardware environment for the simulation experiments is a desktop computer with the main configuration being an Intel i7, 2.9 GHz processor. The software testing environment is a 64-bit Windows 10 system, and the simulation software used is Pycharm. In this test, 8 groups of data in references17 were selected, and each index of each data set was synthesized to obtain the corresponding scoring results and evaluation results of the 8 groups of data indicators shown in Table 3.

Table 3 Index scoring results and evaluation results.
Full size table
  1. F.

    Analysis of simulation results.

The fuzzy analytic hierarchy process is used to compare the indicators pairwise and the fuzzy complementary judgment matrix is obtained using formula (1) are shown in Appendix Table 1.

The weights of the Primary Indicator and Secondary Indicator corresponding to the 8 groups of data obtained by formula (2) are shown in Table 4.

Table 4 Index weight table.
Full size table

The characteristic matrix corresponding to each group is calculated according to Formula (4), as shown in Appendix Table 2.

Then, formula (3) is used to calculate the pairwise consistency and compatibility of the judgment matrices for each group of data, to analyze whether the pairwise comparisons between each group of data meet satisfactory consistency and compatibility. The results of the analysis are shown in Appendix Tables 3 and 4.

It can be seen from Appendix Table 3 that the values of all indicators in all data sets are less than 0.1, so they all meet satisfactory consistency. Therefore, the weight distribution of these data sets is reasonable.

Based on Appendix Table 4, it is found that only the results of \(I({A_{32}},{A_{52}})\) and \(I({A_{52}},{A_{72}})\) are greater than 0.1, indicating unsatisfactory compatibility. The comparison between the judgment matrices shows that the evaluation data of the fifth group of experts is inaccurate and does not satisfy the satisfactory compatibility when compared with other data. Therefore, it should be removed from the final evaluation.

From Appendix Tables 3 and 4, it is found that except for the evaluation data of the fifth group of experts, all other evaluation data meet the two conditions of satisfactory consistency and satisfactory compatibility. Therefore, using their average as the weight allocation vector of factor indicators is reasonable and reliable. After removing the fifth group of data, the final weight vector is obtained by using the average of the remaining evaluation data in formula (5), as shown in Table 5.

Table 5 Final weighting scale.
Full size table

The second weight of the sub-indicators at the second level can be determined using the comparative value function in formula (6). The data from Table 1 is used as the threshold values, and the data from Table 3 is used as the indicator values. Three sets of experimental data are selected with parameters: s = 1/4, t = 0.5; s = 1/4, t = 0.6; s = 1/6, t = 0.6, respectively, to evaluate the comparative values of each second-level sub-indicator. Formula (7) is used to calculate the final evaluation result for the combat data quality. The evaluation results corresponding to each parameter are shown in Fig. 4.

Fig. 4
figure 4

Comparison of the evaluation results of each parameter.

Full size image

According to Fig. 4, it can be observed that before improvement, the parameter s = 1/4, t = 0.5 yields the best evaluation result. Therefore, we select the parameter s = 1/4, t = 0.5 to evaluate the test results of the improved second-level sub-indicator data after excluding the fifth set of data. The results are shown in Table 6.

Table 6 Comparison value and result value table after improvement.
Full size table

By combining Fig. 4 with Table 6. Comparing their simulation results with the standard values, the comparison results are shown in Fig. 5.

Fig. 5
figure 5

Comparison of simulation results and standard values.

Full size image

From Fig. 4, it can be observed that different parameter values of s and t lead to different final results. Simulation results always have errors compared to the standard values. By continuously adjusting the parameter s to change the curve’s rate of change and adjusting t to limit the maximum value of the second-level weight, the results can be closer to the standard values. From the four sets of comparative simulation results in Fig. 5, it can be seen that, after determining the parameters, the simulation results based on the improved FAHP-CVF method with double-weighted indicators are closer to the standard values in Table 3, with a larger degree of improvement in each data item compared to the results before improvement.

To further validate the proposed method, a comparative analysis was conducted with the BPNN method proposed in reference18, the FAHP method proposed in reference6, and the MDM proposed in reference14. The reason for selecting BPNN, FAHP, and MDM for comparison is that these three methods are commonly used algorithms for data quality assessment, providing accurate and reliable evaluation results. They are suitable for solving practical decision-making problems due to their flexibility and scalability, allowing adjustments and improvements based on specific issues, and BPNN is one of the classical algorithms in machine learning algorithm, FAHP is the representative of classical algorithm in subjective weighting method, MDM is the representative of classical algorithm in objective weighting method. Therefore, comparing the proposed method with these three methods better demonstrates its superiority and general applicability. The comparative results are shown in Fig. 6.

Fig. 6
figure 6

Comparison of Algorithm Results.

Full size image

The time and mean square error of each algorithm are shown in Table 7.

Table 7 Comparison results.
Full size table

According to the comparison results in Table 7, the mean square error of the FAHP-CVF method based on the double-weighted method is smaller than that of other methods, and the results are closer to the standard values. To further verify the effectiveness and applicability of the proposed method, statistical analyses were conducted using the Pearson correlation coefficient, Spearman correlation coefficient, significance, and difference indicators based on the results obtained from four methods. The evaluation criteria are as follows:

1) Correlation Coefficient:

  • If the correlation coefficient > 0.8, it indicates a high level of consistency between the two methods.

  • If 0.5 ≤ correlation coefficient < 0.8, it indicates a moderate level of consistency.

  • If the correlation coefficient < 0.5, it indicates significant differences between the two methods.

2) Significance:

  • If significance < 0.05, it indicates a significant correlation, and the results are statistically meaningful.

  • If significance ≥ 0.05, it suggests that the correlation might be random and requires further investigation.

3) Difference:

  • If the difference < 0.05, it indicates a significant difference between the two methods.

  • If the difference ≥ 0.05, it indicates no significant difference between the results of the two methods.

The analysis results are shown in Table 8.

Table 8 Statistical analysis table.
Full size table

Figure 7 shows the results and distribution differences of the two methods using scatter plots and box plots.

Fig. 7
figure 7

Visual presentation.

Full size image

From Table 8; Fig. 7, it can be observed that the Pearson correlation coefficients and Spearman correlation coefficients between FAHP-CVF and BPNN, FAHP, and MDM methods are all greater than 0.8, indicating a high level of consistency between the proposed method and the other three methods. This demonstrates that the proposed method is consistently applicable to combat data quality evaluation, verifying the robustness of the results. The significance values between FAHP-CVF and BPNN, FAHP, and MDM methods are all less than 0.05, indicating that the correlations are significant, and the result similarities are not caused by randomness, confirming their statistical validity. The difference values between FAHP-CVF and BPNN, as well as MDM methods, are greater than or equal to 0.05, indicating that the results of the proposed method are not significantly different from those of the other two methods, further supporting the robustness of the conclusions. Although there is a difference between FAHP-CVF and FAHP, the consistency in correlation coefficients and significance values suggests that the proposed method is an improvement over FAHP. It provides a more scientific and accurate evaluation of combat data quality, demonstrating its effectiveness and practical value.

Conclusion

Due to the inherent complexity of military operations and related issues, data quality problems become particularly prominent in large-scale military simulation and wargaming systems. As the input component of combat simulation systems, the quality of combat data directly impacts the accuracy and validity of the output results. To address the current challenges of inaccurate combat data evaluation, and in light of the limitations in domestic and international data quality evaluation methods, this study proposes a double-weighted based on FAHP optimized by CVF method for evaluating combat data quality. This method enhances the precision of existing combat data quality evaluation approaches. Experimental simulation results demonstrate that the proposed method is easy to understand and implement, with evaluation outcomes that are closer to the standard values. The method holds significant value in combat simulation and wargaming, as it can greatly improve the accuracy of such simulations and has substantial application potential in future military development. The focus of this research is on combat data quality in simulation and evaluation, with the innovation lying in the proposal of a reasonable assessment method for combat data quality. However, the study has certain limitations, such as a relatively small data scale and the influence of subjective factors. Although the limited research data restricts broad applicability, the proposed method itself is generalizable and applicable to any combat simulation evaluation. Future research should expand the dataset to consider a broader range of combat data and operational scenario factors, further optimizing the quality assessment methods and providing robust data support for the development of combat simulation evaluations.