Introduction

Magnetic semoconductors (MSs), which show both properties of semiconductors and ferromagnets, are the main sub-field of spintronics. In past few decades, a variety of thin film and bulk form MSs have been discovered1,2,3,4,5,6. Based on these materials, many interesting phenomena were reported and several spintronic devices were fabricated1,2,3,4,5,6,7,8. The most famous MSs are (Ga,Mn)As thin films that are synthesized through low temperature Molecular Beam Epitaxy (LT-MBE) method9,10. In (Ga,Mn)As, Mn/Ga substitution induces both spins and holes simultaneously and turns the system into ferromagnetic state when the doping level of Mn exceeds \(\sim\) 1%. (Ga,Mn)As behaves as a p-type MS with carrier concentrations of 10\(^{20}\)-10\(^{21}\)/cm\(^{-3}\). Theoretical studies show that the spin-spin exchange interactions in (Ga,Mn)As are mediated by holes and can be enhanced with increasing carrier concentrations11,12. As of today, the highest ferromagnetic transition temperature \(T_C\) observed in (Ga,Mn)As is \(\sim\) 200 K, with the doping level of Mn up to \(\sim\) 12\(\%\)13. In 2012, Tanaka et al. reported the n-type MS (In,Fe)As thin films, in which the spins are induced by Fe while carriers are induced by native defects and non-magnetic donors. That is, the carrier concentration can be regulated while fixing the spin concentration. Their results show that the Curie temperature in (In,Fe)As increases as carrier concentration increases, indicating that the ferromagnetism in (In,Fe)As is mediated by carriers4,14.

In recent years, many series of bulk form MSs with decoupled spins and carriers doping have been reported, e.g. 111-type Li(Zn,Mn)As15 and Li(Zn,Mn)P16, 1111-type (La,Ba)(Zn,Mn)AsO17 and 122-type (Ba,K)(Zn,Mn)2As218,19. Through manipulating the spins’ and carriers’ concentrations separately, the individual dependencies of ferromagnetic ordering on spins or carriers have been carefully studied18,20,21,22. It has been demonstrated that the exchange interactions between spins are mediated by carriers in these bulk form MSs. To achieve the highest Curie temperature, both concentrations of spins and carriers have to be optimized. The highest \(T_C\) observed experimentally in bulk form MSs has been achieved as high as 230 K in (Ba,K)(Zn,Mn)2As219.

The dominant carriers of above mentioned bulk form MSs are holes, that is, they are p-type MSs. In 2019, our group has reported the successful fabrication of a new bulk form n-type MS Ba(Zn,Co)2As223. The highest \(T_C\) reaches \(\sim\) 45 K when the doping level of Co is up to 0.04, and muon spin relaxation (\(\mu SR\)) measurements have confirmed that the ferromagnetic ordering in Ba(Zn,Co)2As2 is homogeneous and intrinsic. In 2021, Fu et al.24 have investigated the manipulation of ferromagnetic ordering in Ba(Zn,Co)2As2 system by negative and positive chemical pressure introduced by isovalent Sb/As and Sr/Ba substitutions, respectively, and found that \(T_C\) increased significantly in Sr-doped Ba(Zn,Co)2As2. In order to investigate the origin of n-type carriers in Ba(Zn,Co)2As2, Zhi et al25. performed systematic first-principles calculations on the electronic structure of Ba(Zn,Co)2As2. It has been found that carriers in Ba(Zn,Co)2As2 emerge when two (or more) Co atoms substitute for Zn atoms at adjacent lattice sites, and the density is predominantly contributed by As-4p orbitals, with subsidiary contributions from the Co-3d orbitals. In addition, Zhi et al. calculated the formation energies (\(E_{f}\)) of Co/Zn substitution and alternative defects, such as Co/Ba substitution and As vacancies25. The calculated results have revealed that comparing with \(E_{f}\) for Co/Ba substitution (\(E_{f}\) \(\sim\) 5.1 eV) and an As vacancy (\(E_{f}\) \(\sim\) 1.9 eV), \(E_{f}\) for Co/Zn substitution is significantly lower (\(E_{f}\) \(\sim\) -0.4 eV). This further confirms that n-type carriers arise from hetero-valent Co/Zn substitution, and not arising from defects. While different to other bulk form p-type MSs, Co doping Ba(Zn,Co)2As2 introduces both spins and electron carriers (confirmed by Hall effect and Seebeck effect measurements23) simultaneously, which makes it difficult to investigate the individual influence of carriers and spins on the formation of ferromagnetism. Therefore, how the ferromagnetism in Ba(Zn,Co)2As2 is mediated by carriers has yet to be investigated.

In this paper, we report the effect of carriers doping on the ferromagnetism in n-type MS Ba(Zn,Co)2As2. Focusing on Ba(Zn0.97Co0.03)2As2 which has a \(T_C\) \(\sim\) 31 K, additional n-type or p-type carriers have been introduced through In/Zn or Cu/Zn substitutions, respectively. The X-ray diffraction results show that all In-doped and Cu-doped samples maintain the high-temperature tetragonal structure. Hall effect measurements confirm that In doping introduces additional n-type carriers, and Cu doping introduces additional p-type carriers. DC magnetization measurements indicate that 2% In/Zn substitution significantly improves \(T_C\) of Ba(Zn0.97Co0.03)2As2 by 16% to 36 K. On the other hand, 1.5% Cu doping obviously suppresses \(T_C\) by 52% to 15 K, and eventually transforms the ferromagnetic ordering into a paramagnetic state with 3% Cu doping. Our experimental results show that the ferromagnetism in n-type MS Ba(Zn,Co)2As2 can be manipulated by additional carriers through non-equivalent chemical doping, not only the concentrations but also the type of carrier.

Fig. 1
figure 1

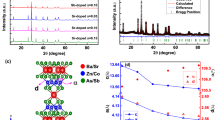
(a) The X-ray diffraction patterns for polycrystalline In-doped Ba(Zn0.97–xCo0.03In\(_{x}\))2As2 (x = 0.01, 0.02, 0.03 and 0.04) and Cu-doped Ba(Zn0.97–xCo0.03Cu\(_{x}\))2As2 (x = 0.015 and 0.03). (b) The crystal structure of BaZn2As2 with high-temperature tetragonal phase. (c) The Rietveld refinement of Ba(Zn\(_{0.95}\)Co0.03In\(_{0.02}\))2As2. (d) The lattice parameters a and c obtained from the Rietveld refinements for both In-doped and Cu-doped samples.

Full size image

Results and discussion

X-ray diffraction

Depending on the synthesis condition, BaZn2As2 exhibits two different crystal structures, the low-temperature orthorhombic phase \(\alpha\) -BaZn2As2 (space group Pnma, metal)26 and the high-temperature tetragonal phase \(\beta\)-BaZn2As2 (space group I4/mmm, semiconductor with a bandgap \(\sim\) 0.2 eV)27,28. We should note that all BaZn2As2-based MSs can be realized only in the tetragonal phase \(\beta\)-BaZn2As2, as reported previously18,23. We conducted X-ray diffraction to determine the crystal structure, and show polycrystalline X-ray diffraction patterns of In-doped Ba(Zn0.97–xCo0.03Inx)2As2 (x = 0, 0.01, 0.02, 0.03 and 0.04) and Cu-doped Ba(Zn0.97–xCo0.03Cu\(_{x}\))2As2 (x = 0.015 and 0.03) samples in Fig. 1a. With In or Cu doping, the peaks just shift slightly and no new peaks are found, which demonstrates that neither In/Zn nor Cu/Zn substitution breaks the tetragonal crystal structure, as shown in Fig. 1b. We also carried out the Rietveld refinements for the X-ray diffraction data of all samples with tetragonal \(\beta\)-BaZn2As2 phase using an open-source package GSAS-II29, and show the Rietveld refinement result of Ba(Zn\(_{0.95}\)Co0.03In\(_{0.02}\))2As2 in Fig. 1c as an example. The resultant weighted reliable factor R\(_{wp}\) is \(\sim\) 6.5%, indicating the good fitting. The lattice parameters a and c can be obtained from the refinements. In Fig. 1d, we show the lattice parameters of all the samples. The obtained lattice constants a = 4.1221 Å and c = 13.5709 Å of the starting compound Ba(Zn0.97Co0.03)2As2 agree well with those reported in previous work23. For In-doped samples, both the lattice constants a and c increase monotonically as the doping level x increases. For Cu-doped samples, with the increasing of Cu doping levels, the lattice constant a increases, while c decreases. We should note that the overall change of lattice parameters is quite small. The unit cell volume just increases \(\sim\) 0.3% at the highest In doping level and decreases \(\sim\) 0.4% at the highest Cu doping level.

Fig. 2
figure 2

(a) Temperature-dependent resistivity of In-doped and Cu-doped Ba(Zn0.97Co0.03)2As2 samples. (b–d) Hall resistivity of (b) Ba(Zn0.97Co0.03)2As2, (c) Ba(Zn\(_{0.94}\)Co0.03Cu0.03)2As2 and (d) Ba(Zn\(_{0.93}\)Co0.03In\(_{0.04}\))2As2.

Full size image

Transport and Hall effect

The temperature-dependent resistivity of both In-doped and Cu-doped Ba(Zn0.97Co0.03)2As2 samples are shown in Fig. 2a. For all In-doped samples, the resistivity increases with the decreasing of temperature, indicating that the samples retain semiconducting behavior. The magnitude of resistivity for In-doped samples decreases significantly with the increasing of In doping level, which agrees with our expectation that In/Zn substitution will induce more carriers. While for Cu-doped samples, the resistivity decreases with temperature decreasing, indicating that the samples change from semiconductor to metal, and the magnitude is much lower than that of In-doped samples in low temperature region. To examine the type and the concentrations of carriers for both In-doped and Cu-doped samples, we carried out the Hall effect measurements, and show the results in Fig. 2b–d. For the starting compound Ba(Zn0.97Co0.03)2As2, due to the poor signal-to-noise ratio in low temperature region, we only show the experimental result measured at 300 K. The negative slope indicates that the dominant carriers are electrons, with a concentration \(\sim\) 6\(\times\) 10\(^{17}\)/cm\(^{-3}\). As shown in Fig. 2c, for Cu-doped sample, the slopes of Hall resistivity curves at different temperature are all positive, indicating that the dominant carriers already change from electrons to holes. The carrier concentration obtained from the slope at different temperatures is quite close, \(\sim\) 3\(\times\) 10\(^{20}\)/cm\(^{-3}\),which agrees with the metallic behavior observed in the resistivity measurement. While for In-doped samples, as shown in Fig. 2d, the n-type carriers are confirmed by Hall resistivity results as the slope is negative. The carrier concentration also increases with temperature increasing, which is also consistent with the semiconducting behavior. The carrier concentration at 300 K is \(\sim\) 2\(\times\) 10\(^{19}\)/cm\(^{-3}\), two orders higher than that of Ba(Zn0.97Co0.03)2As2. According to the formula \(\sigma = ne\mu\), where \(\sigma\), n, e and \(\mu\) represent electrical conductivity, carrier concentration, elementary charge and carrier mobility, respectively, we calculate the carrier mobility of Ba(Zn0.97Co0.03)2As2 and Ba(Zn\(_{0.93}\)Co0.03In\(_{0.04}\))2As2 at 300 K that are 3.6 \(\text {cm}^2/\text {V} \cdot \text {s}\) and 8.5 \(\text {cm}^2/\text {V} \cdot \text {s}\), respectively. The improvement in carrier mobility is likely attributed to increased carrier concentration, which enhances the screening effect, thereby weakening the carrier scattering30. Our results demonstrate that In/Zn substitution induces more n-type carriers and conserves the semiconducting behavior in Ba(Zn0.97–xCo0.03In\(_{x}\))2As2, while Cu/Zn substitution induces p-type carriers and turns the semiconductor to metal in Ba(Zn0.97–xCo0.03Cu\(_{x}\))2As2.

Magnetic properties

In Fig. 3a, we show the temperature-dependent DC magnetization for both In-doped and Cu-doped samples measured in field cooling (FC) modes under an applied external field of 100 Oe. Above 60 K, no magnetic instability can be observed for all samples. At lower temperatures, sharp increase appears, indicating the onset of ferromagnetic ordering. In the inset of Fig. 3a, we can see clearly the evolution of ferromagnetic transition with the doping level x. Compared with the starting compound Ba(Zn0.97Co0.03)2As2, the transition temperature shifts to higher temperature region with In doping level increasing from 0 to 0.02, and then remain almost unchanged. In contrast, the transition temperature quickly shifts to lower temperature region with 1.5% Cu doping. When Cu-doping level reaches 0.03, the ferromagnetic transition is completely suppressed; The magnetization at 2 K is only 0.0043\(\mu _{B}\)/Co, which is two orders of magnitude smaller than that of the starting compound Ba(Zn0.97Co0.03)2As2. In Fig. 3(b) and (c), we show the iso-thermal magnetization curves M(H) for both In-doped and Cu-doped samples measured at 2 K. Clear hysteresis loops can be observed in Cu-doped sample with doping level x = 0.015 and all the In-doped samples, which demonstrates the ferromagnetic ordering state. The coercive field of these samples are quite small, \(\sim\) 10 Oe, comparable to that of the starting compound Ba(Zn0.97Co0.03)2As2. Such a small coercive field is good for spin manipulation. For the sample with 3% Cu doping, no hysteresis loop can be observed, which indicates that the ground state has been transformed into a paramagnetic state. We fit the paramagnetic part of the T-dependent magnetization data with a modified Curie–Weiss formula, \((\chi -\chi _{0})^{-1}=(T-\theta )/c\), \({\chi }_\mathrm{{0}}\), C and \(\theta\) represent the temperature-independent term, the Curie constant, and the Weiss temperature, respectively. From the fitting results, we can obtain the Weiss temperature θ and the effective momentum \(\mu _{eff}\) by using the formula \(C=N\mu _{0}\mu _{eff}^{2}/3k_{B}\). The effective momentum \(\mu _{eff}\) is \(\sim\) 1.4-1.7 \(\mu _{B}\)/Co, which is close to the expected value of 1.7 \(\mu _{B}\)/Co for S = 1/223. Based on the experimental observation of the magnetization of 0.2-0.3 \(\mu _{B}\)/Co in M(T) curves at 2 K, we think that antiferromagnetic interactions exist between certain Co ions in the system. Specifically, the competition between ferromagnetic and antiferromagnetic interactions results in the reduced magnetization. The evolution of the Weiss temperature \(\theta\) can also be seen clearly through the linear fitting of the reverse of \((\chi -\chi _{0})\) versus temperature in the high temperature region, which is plotted in Fig. 4a and b. \(\theta\) can be read from the the intersections of the linear fitting lines and x axis. In Fig. 4c and d, we show the dM(T)/dT versus temperature curves for all the samples, and the Curie temperature \(T_C\) were defined as the temperatures where dM(T)/dT versus T curve shows a minimum.

Fig. 3
figure 3

(a) Temperature dependent DC magnetization for In-doped and Cu-doped samples in FC mode with an applied external field of 100 Oe. Inset shows the enlarged curves of 2 K to 60 K region. (b) The isothermal magnetization curves M(H) measured at 2 K for both In-doped and Cu-doped samples. (c) Partial enlarged M(H) curves with external field from − 60 Oe to 60 Oe.

Full size image

We tabulate the Curie temperature \(T_C\), the Weiss temperature \(\theta\), the effective moment \(\mu _{eff}\) and \(M_{2K}\) (the M value measured at T = 2 K and H = 100 Oe in FC condition) in Table 1. We can see that both \(T_C\) and \(\theta\) reach a maximum at x = 0.02 for In-doped samples, and then \(T_C\) remain unchanged while \(\theta\) slightly rollback with more In doping. For x \(\ge\) 0.02, the variation of both \(T_C\) and \(\theta\) is quite small (less than 2 K). In some cases, over-doping carriers may suppress the ferromagnetic ordering, which has been experimentally verified in some bulk form MSs like Li(Zn,Mn)P22 and Li(Cd,Mn)P31. The carrier-mediated ferromagnetism can be described by the RKKY-like exchange interaction as J \(\sim\) cos(2\(k\) \(_{F}\) \(r\))/\(r\) \(^{3}\), where \(k\) \(_{F}\) is the radius of Fermi surface and r is the distance between localized spins. Extra carriers will modify the Fermi surface, thus affects the value of J, and then the ferromagnetic ordering. While for Cu-doped samples, both \(T_C\) and \(\theta\) decrease rapidly with the increasing of Cu doping level, and reach nearly 0 for x = 0.03, indicating the disappearence of ferromagnetism. Combining the results of In/Zn and Cu/Zn substitutions in Ba(Zn0.97Co0.03)2As2 together, we can readily find that appropriate In/Zn substitution enhances the Curie temperature of ferromagnetic ordering, while Cu/Zn substitution suppresses the ferromagnetic ordering.

Fig. 4
figure 4

(a, b) \((\chi -\chi _{0})^{-1}\) versus temperature plots for Cu-doped and In-doped samples. Straight lines show the linear fitting, and the fitting temperature range is from 100 K to 200 K. (c, d) dM(T)/dT versus temperature plots for Cu-doped and In-doped samples. \(T_{C}\) were determined as the temperature showing a minimum of these curves.

Full size image
Table 1 The Curie temperature \(T_C\) from the minimum value of dM(T)/dT, the Weiss temperature \(\theta\), the effective moment \(\mu _{eff}\) from Curie–Weiss fit and the base magnetization \(M_{2K}\) measured at 2 K under FC mode for different doping levels x.
Full size table

Summary

In previous report, the ferromagnetic ordering in Ba(Zn,Co)2As2 can be manipulated by chemical pressure24, and the isovalent Sb/As and Sr/Ba substitutions don’t induce extra carriers directly. The experimental results have revealed that Sb/As substitution induces negative chemical pressure through expanding lattice, which results in the decreasing of \(T_{C}\); While Sr/Ba substitution induces positive chemical pressure through compressing lattice, which results in the increasing of \(T_{C}\). In current work, In/Zn substitution induces extra n-type carriers and Cu/Zn substitution induces extra p-type carriers, but the variation of unit cell volume is very small, which is only \(\sim\) 0.3% for the highest In doping level x = 0.04 and \(\sim\) 0.4% for the highest Cu doping level x = 0.03; That means doping In or Cu introduces very small chemical pressure. The Curie temperature \(T_{C}\) for Ba(Zn0.97Co0.03)2As2 is defined as 31 K by reading from the minimum of dM(T)/dT versus T curves. We can see that 2% In/Zn substitution increases \(T_{C}\) by 16% from 31 K to 36 K. But for the highest Cu doping level x = 0.03, the ferromagnetic ordering has even been completely suppressed and transformed into a paramagnetic state, which is much more significant than the effect on \(T_{C}\) by negative chemical pressure induced by Sb/As substitutions.

To summerize, in this work, based on n-type MS Ba(Zn0.97Co0.03)2As2, In/Zn and Cu/Zn substitution have been designed, and the doping effects have been investigated. Our X-ray diffraction results have demonstrated that both In and Cu dopings will not affect the tetragonal crystal structure, and the lattice parameters do not change much at the highest doping levels of In and Cu. Through the Hall effect measurements, we find that In doping introduces additional electron carriers into the system, and improves the Curie temperature from 31 K to 36 K at the doping level x = 0.02, that is, 2% In doping into Ba(Zn0.97Co0.03)2As2 improves \(T_C\) by 16%. With more In doping, the magnitude of resistivity is decreasing, while the Curie temperature \(T_C\) does not linearly increase, and the ferromagnetic ordering display RKKY-like exchange interactions. On the other hand, Cu doping induces extra hole carriers, which eventually suppresses the ferromagnetic ordering in Ba(Zn0.97Co0.03)2As2 at the doping level of 3% Cu. Our work experimentally demonstrated that the mechanism of the ferromagnetic long range ordering in Ba(Zn\(_{1-x-y}\)Co\(_{x}\)In\(_{y}\))2As2 are consistent with the general carrier mediated ferromagnetism picture that has been proposed for MSs3,8, and the ground state can be effectively manipulated by carriers’ densities. This finding is helpful to understand the general mechanism responsible for the long range ferromagnetic ordering in all magnetic semiconductors.

Methods

Material synthesis

In-doped Ba(Zn0.97–xCo0.03In\(_{x}\))2As2 and Cu-doped Ba(Zn0.97–xCo0.03Cu\(_{x}\))2As2 polycrystalline samples were synthesized through conventional solid-state reaction method, similarly to that of Ba(Zn,Co)2As223. Starting materials Ba pieces, In, Zn, Co, As, Cu powders were well mixed according to the elementary ratio and transferred to alumina crucibles and finally sealed in evacuated silica tubes. The mixture was heated at 1150 \(^{\circ }\)C for 25 h followed by cooling to room temperature. The obtained products were then grounded, pressed into pellets with 8 mm in diameter, placed in aluminum crucibles, then sealed in evacuated silica tubes and reheated at 1150 \(^{\circ }\)C for another 25 h for sufficient reaction. After heating, the samples were quickly cooled to room temperature through quenching in the water to stabilize the high-temperature phase, tetragonal \(\beta\)-BaZn2As232.

Experimental characterization

The X-ray diffraction (XRD) measurements were carried out on a PANalytical powder X-ray diffractometer with monochromatic Cu-K\(_{\alpha 1}\) radiation. The DC magnetization measurements were conducted on a Quantum Design Magnetic Property Measurement System (MPMS-3). The Hall effect was measured on a Quantum Design Physical Property Measurement System (PPMS). The electrical resistivity was measured using the typical four-probe technique.