Improving time series forecasting in frequency ___domain using a multi resolution dual branch mixer with noise insensitive ArcTanLoss

Zhang, Yahao; Zhou, Xiaofeng; Zhang, Yichi; Li, Shuai; Liu, Shurui

doi:10.1038/s41598-025-95529-2

Download PDF

Article
Open access
Published: 12 April 2025

Improving time series forecasting in frequency ___domain using a multi resolution dual branch mixer with noise insensitive ArcTanLoss

Yahao Zhang^1,2,3,
Xiaofeng Zhou^1,2,
Yichi Zhang^1,2,
Shuai Li^1,2 &
…
Shurui Liu^1,2,3

Scientific Reports volume 15, Article number: 12557 (2025) Cite this article

1822 Accesses
Metrics details

Subjects

Abstract

Enhancing the accuracy of long-term time series forecasting is a crucial task across various fields. Recently, many studies have employed the Discrete Fourier Transform (DFT) to convert time series into the frequency ___domain for forecasting, as it provides a compact and efficient representation, enabling the capture of deep cyclical patterns and global trends that are often difficult to identify in the time ___domain. However, the frequency ___domain information in time series has yet to be fully explored due to three main reasons: they rely on a fixed-resolution DFT, which restricts them to a single frequency resolution and leads to the loss of essential information; they predominantly focus on global dependencies while overlooking local temporal details; they remain highly sensitive to noise in the time series, limiting the model’s ability to capture stable patterns. In this paper, we propose a novel lightweight architecture (FreMixer) that operates entirely in the frequency ___domain. Firstly, we introduce a multi resolution segmentation mechanism in the frequency ___domain, enabling features represented at different resolutions to complement each other, effectively overcoming the sparse resolution limitations of DFT in the frequency spectrum. Secondly, we comprehensively extract the frequency information by employing a dual branch architecture that simultaneously captures both global and local features at each frequency resolution, providing a more comprehensive representation of temporal patterns. Moreover, we propose a noise insensitive loss function ArcTanLoss that reduces overfitting to outliers. Extensive experiments conducted on seven different datasets have validated the effectiveness of our proposed model and loss function.

A multiscale model for multivariate time series forecasting

Article Open access 10 January 2025

Consistency regularization for few shot multivariate time series forecasting

Article Open access 23 April 2025

Sparse transformer with local and seasonal adaptation for multivariate time series forecasting

Article Open access 10 July 2024

Introduction

Time series forecasting is a long-standing task that has been widely applied in multiple fields such as economics^1,2, weather forecasting^3,4,5, financial markets^6,7, and energy management^8,9,10,11. Specifically, long-term time series forecasting (LTSF) plays a pivotal role in deciphering trends over extended periods, which is crucial for decision support systems¹². The core challenge in long-term time series forecasting involves extracting useful patterns from historical observations and using these patterns to predict future events. The complexity of this task arises from the noise often contained in time series data and the dynamics of the data which may change over time. Therefore, prediction models must be able to extract key features from complex and outlier-rich data and handle potential non-linear relationships and non-stationarities.

In the field of time series analysis, it is widely acknowledged that time series data can be depicted in the time ___domain and equivalently transformed into the frequency ___domain for comprehensive analysis. In contrast, the frequency ___domain offers a more compact representation of time series. Each frequency component is characterized by its amplitude and phase. This provides a new perspective for time series prediction, making it particularly advantageous for accurately capturing long-term trends and seasonal patterns in time series. For example, FITS¹³ transforms time series into the frequency ___domain and employs a low-pass filter to remove high-frequency noise, achieving superior performance with reduced memory and computational costs.

However, the frequency ___domain information in time series has yet to be fully explored, since models based on the frequency ___domain face several issues: (1) Limited frequency resolution: DFT provides a frequency ___domain perspective for time series analysis. However, existing methods typically use single frequency resolution by applying a fixed-length time window for Fourier transforms. This limitation might lead to the loss of essential information, impairing the accurate recognition and analysis of the signal’s authentic frequency components. (2) Inadequate modeling of local information: Time series data contain both long-term global trends and transient local characteristics, both of which are crucial for the performance of forecasting models^14,15. Global dependencies refer to relationships spanning longer time segments in the series, reflecting overall trends and seasonal patterns. For example, a time series may show a clear global trend where certain time points are influenced by others at specific periodic intervals. Meanwhile, local dynamics refer to fluctuations within short periods in the series, revealing how the series responds to sudden events and adjusts its behavior in the short term. Many models only focus on global trends, leading to an incomplete understanding of time series dynamics. (3) Sensitivity to high-frequency noise. Existing time series forecasting models typically use Mean Square Error (MSE) as a loss function to optimize the best balance between prediction results and ground truth. However, time series data often encounter sudden fluctuations within certain periods, particularly in highly variable non-stationary environments¹⁶. Since the gradient of MSE is linearly proportional to errors, large deviations caused by anomalies or extreme fluctuations can disproportionately influence the model’s optimization process. This often leads to overfitting to these anomalies, preventing the model from capturing broader and more stable data patterns.

To address the aforementioned issues, we introduce the Frequency Domain Mixer (FreMixer), a lightweight model that operates entirely in the frequency ___domain, with three key components: Multi Resolution Segmentation Block, Dual Branch Extractor Block, and ArcTanLoss. Similar to PatchTST¹⁷, FreMixer leverages segment operations and further introduces a multi resolution segmentation mechanism to capture comprehensive frequency ___domain information. Unlike previous models, FreMixer adopts a parallel architecture to integrate information across segments, enabling it to capture both long-term stable cycles and short-term local variations. Furthermore, FreMixer employs ArcTanLoss for training, which improves the model’s ability to fit mid-to-low frequency trends by sacrificing the fitting precision for volatile data points. The principal contributions of this study can be summarized as follows:

We introduce a multi resolution frequency ___domain architecture. By dividing time series into multiple segment groups of varying lengths, FreMixer enables the extraction of frequency features at multiple resolutions. This approach allows the frequency components from different levels to complement one another, resulting in a richer and more comprehensive representation of the data.
We design a frequency ___domain feature extractor with a dual branch strategy: one branch processes input sequences from a local window perspective to focus on temporal details, while the other branch attends to the entire time series globally, capturing long-term dependencies. This design balances the preservation of local temporal features with the modeling of global trends.
Inspired by the properties of the arctan function, we propose a novel noise insensitive loss function, ArcTanLoss, designed to mitigate overfitting to outliers. Unlike traditional loss functions, such as MSE, which often exhibit unbounded gradients in response to large errors, ArcTanLoss provides a bounded gradient response, effectively limiting the influence of extreme deviations. This allows the model to focus on capturing the underlying data patterns while reducing its sensitivity to noise and anomalies, significantly enhancing its generalization capabilities.
Extensive experiments have been conducted on various real-world datasets, demonstrating state-of-the-art performance and proving the effectiveness and efficiency of the proposed architecture. Additionally, comprehensive ablation studies validate the contribution of each component, confirming their individual effectiveness.

Related work

Due to the importance of time series forecasting, researchers have proposed various models for time series forecasting. Early approaches relied on statistical methods such as ARIMA¹⁸and Holt-Winters¹⁹, which were effective for simple data. With the enhancement of computational power and the increase in data volume, more and more deep learning-based models have been proposed and applied to time series forecasting tasks, including RNN-based models^20,21,22,23, CNN-based methods^14,24, Transformer-based methods^{17,25,26,27,28}, and MLP-based methods^13,29,30. Additionally, the frequency ___domain, as a new perspective for observing time series, can effectively capture periodicity, trend components, and features at different frequencies. Therefore, combining deep learning methods with frequency ___domain analysis has become an important research direction. Furthermore, regardless of the model chosen, selecting an appropriate loss function is crucial for the model’s forecasting performance. In the following sections, we will delve into the various deep learning approaches, frequency ___domain techniques, and loss functions used for time series forecasting. Finally, we summarize the advantages and disadvantages of these methods and explain how FreMixer addresses the issues present in existing approaches.

Deep learning methods for time series forecasting

Deep learning methods have become widely used in time series forecasting over the past few years due to their powerful feature learning capabilities. RNN-based models^20,21,22,23, such as LSTM²² and GRU²³, are intuitively the primary methods for modeling temporal dependencies. However, these autoregressive models suffer from error accumulation and limited global context understanding in long-term forecasting. In recent years, models like Autoformer²⁷ have demonstrated the ability to capture long-range dependencies in time series using Transformer^{25,26,27,28,31}. Additionally, PatchTST¹⁷ improves forecasting by dividing the series into smaller segments, which not only addresses issues of semantics but also enhances network performance. Despite their strengths, Transformer-based models are often complex and fail to capture local dynamics inherent in time series. In contrast, CNN-based models^14,24 excel at capturing the local characteristics of time series. For example, TimesNet¹⁴ transforms time series into 2D tensors and uses multiple convolutional kernels to extract temporal variation features within a period and across adjacent periods. MICN²⁴ performs multi-scale local context modeling of time series using downsampling and upsampling processes combined with 1D convolutional layers. Recently, DLinear²⁹ challenges the efficacy of other methods by providing a simpler linear layer, outperforming previous models. Furthermore, TSMixer³² utilizes MLPs and mixing operations across both time and feature dimensions to efficiently extract information. However, these Linear-based models still face limitations, including a single level of representation and an inability to effectively capture local patterns.

Frequency ___domain forecasting methods

DFT transforms data into the frequency ___domain, allowing researchers to analyze cyclical patterns and long-term trends from a new perspective, which has inspired the development of various deep learning models that leverage frequency ___domain information to improve time series forecasting. Zhang et al.³³ decomposes the hidden states of the LSTM memory cell into multiple frequency components, with each component modeling a specific frequency of the underlying trading patterns that drive stock price fluctuations. Autoformer²⁷ leverages Fast Fourier Transform (FFT) to compute the autocorrelation coefficients of a sequence, employing a sequence-level self-attention mechanism to uncover seasonal similarities at the subsequence level. FEDformer²⁸ introduces the frequency-___domain enhanced attention module, replacing traditional self-attention and cross-attention modules to effectively capture key patterns within the frequency ___domain. TimesNet¹⁴ maps the input length to the output length and utilizes FFT to identify dominant frequencies. It segments the time series based on these frequencies and employs a 2D CNN to model the relationships between adjacent periodic segments. ETSformer³⁴ introduces frequency attention to replace the self-attention mechanism in vanilla Transformers, helping it capture the primary seasonal patterns of time series and thereby enhancing forecasting accuracy. FiLM³⁵ applies Legendre polynomial projections to approximate historical information and uses Fourier projections to filter out noise, incorporating a low-rank approximation to speed up computations. FITS¹³ transforms time series into the frequency ___domain using FFT and employs a complex-valued linear layer to learn amplitude scales and phase shifts. By integrating a low-pass filter to reduce high-frequency noise, FITS maintains a simplified model while delivering performance comparable to PatchTST, but there is still room for improvement. In summary, while many models have improved feature representation by integrating frequency modules, further advancements are needed to more effectively extract multi resolution features and capture local dynamics.

Loss function

Currently, while research on deep learning prediction models primarily focuses on optimizing model architectures, the choice of loss functions is equally crucial, yet it often does not receive adequate attention. Typically, many studies directly employ evaluation metrics such as Mean Squared Error (MSE) or Mean Absolute Error (MAE) as substitutes during the model training process. Some studies have recognized the importance of loss functions and have attempted to replace them. For example, Gong et al.³⁶ combines MSE and MAE in a 1:1 ratio, balancing the two metrics. Dynamic Time Warping(DTW)³⁷ computes the shortest path between two time series using dynamic programming, allowing for warping and stretching along the time axis at different positions, thereby directly measuring the similarity between the predicted and true sequences. TILDE-Q³⁸ employs three different loss items for shape-aware representation learning, ensuring the model remains invariant to amplitude shifts, phase shifts, and uniform scaling, thus better capturing the shape of time series data. Moreover, Park et al.¹⁶ observed the disruptions caused by sudden changes to model predictions, proposing a reweighted framework that adjusts the loss weight based on local density to decrease the weight of losses caused by sudden changes between the lookback and forecast windows while increasing the weight for losses under normal conditions. Mo et al.³⁹ introduced the smooth quadratic loss that strategically adjusts gradients to avoid overfitting, but when the prediction error is large, the gradients become excessively small and may hinder the model’s ability to effectively capture the overall trend. Therefore, for datasets with substantial noise, further study on outlier-insensitive loss functions is necessary.

Significance of this work

In Table 1 we coarsely present a comparison of different models, highlighting their distinct strengths and weaknesses across various dimensions. None of the previous models can simultaneously capture both local and global information across multiple levels effectively. In contrast, FreMixer uses a multi resolution segmentation module to transform the time series into groups of segments with different lengths, and employs a dual branch extractor consisting of linear and convolutional layers to simultaneously capture both global and local frequency ___domain information at multiple levels. Furthermore, the loss functions employed by previous models are often overly sensitive to outliers in time series data, compromising their robustness. To address this issue, we propose ArcTanLoss, a loss function robust to outliers, which improves the model’s forecasting robustness by reducing the gradient at outlier points.

Table 1 Comparison of different models.

Full size table

Methods

This section presents a comprehensive introduction to the proposed FreMixer method and involved components. We begin by presenting the overall framework of FreMixer. Then, we discuss the theory related to the frequency ___domain and the effectiveness of multi resolution segmentation for time series. Subsequently, we introduce the Dual Branch Extractor Block, which consists of a Global Patch Mixer to capture global information and a Local Patch Mixer to capture local information. Next, we employ a Fourier linear layer for efficient prediction. Finally, we discuss the limitations of commonly used loss functions in time series forecasting and propose ArcTanLoss, a noise insensitive loss function.

Framework

The task of multivariate time series forecasting involves utilizing the historical observation sequence $\textbf{X}_I \in \mathbb {R}^{L \times N}$ to predict future values $\textbf{Y} \in \mathbb {R}^{T \times N}$, where L and T represent the lengths of the historical horizon and the prediction horizon, respectively, and N represents the number of observed variables.

The overall framework of FreMixer is presented in Fig. 1. We adopt a channel-independent strategy, which has been demonstrated to be more effective⁴⁰. From the perspective of channel independence, we separately input the data from N channels of the time series into the network, where the input data $\textbf{X} \in \mathbb {R}^L$. Besides, We employed RevIN⁴¹ to deal with distribution shift problem, which has been widely applied in numerous studies. The backbone network first leverages a Multi Resolution Segmentation Block, which segments the input $\textbf{X}$ into multiple groups of segments at different frequency resolutions, denoted as $\{ \textbf{X}_{in}^1, \textbf{X}_{in}^2,..., \textbf{X}_{in}^M \}$. Each group of segments, $\textbf{X}_{in}^i$, is then fed into a distinct branch for further extraction of frequency-___domain information from the time series. This multi-branch architecture facilitates the learning of representations at varying frequency resolutions, enhancing the model’s ability to capture complex temporal patterns. Subsequently, the segmented inputs are processed through multiple Dual Branch Extractor Blocks, which are designed to capture long-term temporal dependencies via global patch mixing, while simultaneously modeling local temporal relationships through patch-wise convolution. Finally, similar to FITS¹³, we utilize a Fourier prediction head for forecasting. The network is trained using the proposed ArcTanLoss, a novel loss function specifically designed to be robust to noise, ensuring stable performance in the presence of outliers.

Frequency multi resolution

Priliminary: complex frequency ___domain

Given a sequence of length N, ${x[n]}_{0 \le n < N}$ (collected from the real world through sensors), its DFT result, $\mathcal {F}(x[n])$, is defined as

$$\begin{aligned} X[k] = \sum _{n=0}^{N-1} x[n]e^{-i \frac{2\pi }{N}nk},\quad k = 0, 1, \ldots , N-1 \end{aligned}$$

(1)

This formula indicates that the sequence’s representation in the frequency ___domain can be obtained through a weighted sum of its time ___domain samples, where the weights are complex exponential functions corresponding to integer multiples of the fundamental frequency component, represented by $e^{i \frac{2\pi }{N}}$. In this context, e signifies the base of natural logarithms, i represents the imaginary unit, and $\cos$, $\sin$ stand for the cosine and sine functions, respectively. Thus, the k-th frequency component $e^{i \frac{2\pi }{N}k}$ corresponds to the k-th sampling point of the sequence’s Z transform on the unit circle, with a sampling interval of $\frac{2\pi }{N}$. Based on the frequency ___domain representation, the Inverse Discrete Fourier Transform (IDFT) allows the reconstruction of the original time-___domain sequence, which can be expressed mathematically as:

$$\begin{aligned} x[n] = \frac{1}{N} \sum _{k=0}^{N-1} {X}[k] e^{i 2\pi \frac{nk}{N}}, \quad n = 0,1,\ldots ,N-1 \end{aligned}$$

(2)

By applying Euler’s formula, the exponential term $e^{i \frac{2\pi }{N}nk}$ can be expressed as a combination of cosine and sine functions:

$$\begin{aligned} e^{i \frac{2\pi }{N}nk} = {\cos {\frac{2\pi }{N}nk}} + i {\sin {\frac{2\pi }{N}nk}} \end{aligned}$$

(3)

This allows us to rewrite both the DFT and IDFT in terms of trigonometric functions as follows:

$$\begin{aligned} X[k] = \sum _{n=0}^{N-1} x[n] \left[ {\cos {\frac{2\pi }{N}nk}} - i {\sin {\frac{2\pi }{N}nk}}\right] \end{aligned}$$

(4)

$$\begin{aligned} x[n] = \frac{1}{N} \sum _{k=0}^{N-1} {X}[k] \left[ {\cos {\frac{2\pi }{N}nk}} + i {\sin {\frac{2\pi }{N}nk}} \right] \end{aligned}$$

(5)

From these expressions, it is clear that an N-point sampled sequence x[n] is composed of a series of sampled points of sine and cosine functions with angular frequencies $\frac{2\pi }{N}k, \quad k = 0, 1, \ldots , N-1$. In other words, the DFT and IDFT decompose the time-___domain signal into a linear combination of sine and cosine waves of different frequencies.

Multi resolution segmentation block

In the realm of Fourier analysis, frequency ___domain resolution refers to the minimum frequency difference that can be discerned between two frequency components. This critical parameter significantly influences the capacity to detect and recognize the various frequency components present within a signal. For a N-point series, the spectral resolution is quantified as $\frac{2\pi }{N}$. To enhance spectral resolution, two primary strategies can be employed: (1) Increasing the sampling frequency, which, by allowing data to be recorded within a fixed time span, enables the addition of more sampling points without altering the total sampling time span, thus improving the frequency ___domain resolution. (2) Increasing the number of sampling points by extending the sampling time, while keeping the sampling rate fixed.

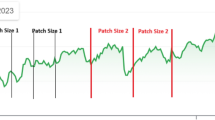
Hence, for a time series with a fixed sampling rate, we segment the historical time window into groups of patches with varying lengths, as shown in Fig. 2. The variation in the length of these patch divisions leads to distinct frequency resolutions being generated. With each patch division strategy featuring a unique fundamental frequency component, the ability of trigonometric functions at varying angular frequencies to represent information can synergistically enhance one another.

Considering the critical role of multi resolution in the frequency ___domain for deep representation of time series, we introduce the Multi Resolution Segmentation Block. We define a set $\textbf{D}= \{ D_1, D_2,..., D_M \}$, containing M patch sizes, representing the patch length for each patch division strategy. Given a time series $\textbf{X} \in \mathbb {R}^L$ and $D_i$, the series is partitioned into multiple patches as $X^i=(x^{i, 1}, x^{i, 2},..., x^{i, P_i}) \in \mathbb {R}^{P_i \times D_i}$, where $P_i = \frac{L}{D_i}$ indicates the number of patches into which the time series of length L will be divided. Subsequently, we acquire the frequency ___domain representation for each patch via FFT:

$$\begin{aligned} \textbf{X}_{in}^{i} = \operatorname {FFT}(\textbf{X}^i) \in \mathbb {C}^{P_i \times \left( \frac{D_i}{2} + 1 \right) } \end{aligned}$$

(6)

As depicted in Fig. 2, the variation of patch sizes corresponds to specific sampling intervals on the unit circle in the complex plane. This variation ensures that each division strategy maintains its own distinct frequency ___domain resolution.

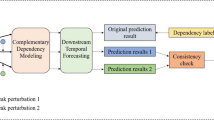
Dual branch extractor block

To capture long-term dependencies and short-term dynamics, we design a Dual Branch Extractor. FreMixer integrates M Dual Branch Extractors, each corresponding to a patch division strategy defined in the Multi Resolution Segmentation Block, ensuring comprehensive coverage across different levels of time series. Our dual branch extractor operates in the complex ___domain, and Fig. 3 illustrates the information extraction process of the Dual Branch Extractor Block.

Global patch mixer

Given the input data at level i, $\textbf{X}_{in}^{i} = \operatorname {FFT}(\textbf{X}^i) \in \mathbb {C}^{P_i \times \left( \frac{D_i}{2} + 1 \right) }$, the Intra Patch Mixer projects each patch’s frequency ___domain representation into a hidden feature space, still dimensioned at $\mathbb {C}^{P_i \times \left( \frac{D_i}{2} +1 \right) }$. This process is accomplished through a fully connected layer, represented as ${\textbf{X}}_{g, intra1}^{i}=\operatorname {FLinear}({\textbf{X}}_{in}^{i})$, where $\operatorname {FLinear}(\cdot )$ denotes a complex linear transformation layer with weights of dimensions $\left( \frac{D_i}{2} +1 \right) \times \left( \frac{D_i}{2} +1 \right)$. By transforming the frequency-___domain data into a more informative feature representation, this step ensures that each patch’s frequency-___domain information is fully expressed, laying a solid foundation for subsequent inter-patch feature mixing.

Time series data often contains complex periodic and trend variations, which are not confined to a single time segment but span across multiple time periods. By allowing each time segment to interact with all other time segments, the model can identify and capture the long-term dependencies within the data, thereby constructing a more comprehensive global feature representation. To further explore the interrelationships between different patches and their effects in the frequency ___domain, we introduce the Global Inter Patch Mixer module. As shown in the right half of Fig. 3, in the Global Inter Patch Mixer, each time segment interacts with all other segments, with blue dashed lines delineating the extent of global interactions. This module is implemented with a shared complex linear layer $\operatorname {FLinear}\left( \cdot \right)$ with dimensions $P_i \times P_i$. The specific operation is as follows:

$$\begin{aligned} \textbf{X}_{g,inter}^{i}=\operatorname {Transpose}\left( \operatorname {FLinear}\left( \operatorname {Transpose}\left( \textbf{X}_{g,intra1}^{i}\right) \right) \right) \end{aligned}$$

(7)

Since the weights of this linear layer are shared across all frequency components by applying the same weights to each frequency component, this design helps the model learn patterns that are commonly present across the entire input sequence frequency spectrum. Through this process, the Global Inter Patch Mixer provides an effective method to comprehensively understand and represent the global structure and dynamics of the time series, offering a rich and powerful feature representation for the final prediction task.

During the Global Inter Patch Mixer process, the frequency components of the segments are independently interacted with the corresponding frequency components from other segments. Following this, another Intra Patch Mixer is employed to fuse these independently processed frequency components, ensuring effective interaction and integration of features. This process is implemented through a complex linear layer, expressed as $\textbf{X}_{g,intra2}^{i}=\operatorname {FLinear}\left( {\textbf{X}}_{g,inter}^{i}\right)$. Subsequently, each patch is mapped back from the frequency ___domain to the time ___domain using IFFT, where $\textbf{X}_{g,time}^{i} = \operatorname {IFFT}\left( \textbf{X}_{g,intra2}^i\right) \in \mathbb {R}^{P_i \times D_i}$. Finally, a flattening operation is performed to produce the output of this level, resulting in $\textbf{X}_{g}^{i} = \operatorname {Flatten}\left( \textbf{X}_{g,time}^{i}\right) \in \mathbb {R}^{L}$.

Local patch mixer

Similar to the Global Patch Mixer, for the input data at level i, $\textbf{X}_{in}^{i} = \operatorname {FFT}(\textbf{X}^i) \in \mathbb {C}^{P_i \times \left( \frac{D_i}{2} + 1 \right) }$, we employ an Intra Patch Mixer to project it into a latent feature space, effectively enhancing the frequency components within each patch. This transformation is performed using a fully connected layer, expressed as $\textbf{X}_{l, intra1}^{i} = \operatorname {FLinear}(\textbf{X}_{in}^{i}) \in \mathbb {C}^{P_i \times \left( \frac{D_i}{2} +1 \right) }$, where $\operatorname {FLinear}(\cdot )$ denotes a complex-valued fully connected layer with weight dimensions of $\left( \frac{D_i}{2} +1 \right) \times \left( \frac{D_i}{2} +1 \right)$.

In time series, many significant trends and relationships occur within limited time spans, such as immediate fluctuations or transitions. By utilizing a sliding window technique, the data is analyzed in smaller, overlapping segments, enabling the model to detect short-term variations and patterns within the time series. Thus, in contrast to the Global Inter Patch Mixer, which captures global dependencies through a fully connected layer, the Local Inter Patch Mixer utilizes a complex convolutional layer $\operatorname {FConv}\left( \cdot \right) _{k_i}$ to focus on extracting local features, where $k_i$ represents the convolution kernel size at layer i, which determines the time span of the segments considered. As shown in the right half of Fig. 3, the range covered by the red solid lines corresponds to the local receptive field of the convolutional layer. This design limits the interaction of each patch to only a few neighboring patches rather than all others globally, effectively addressing the short-term variability and local dependencies inherent in time series data. This process can be formalized as

$$\begin{aligned} \textbf{X}_{l, inter}^{i}=\operatorname {Transpose}\left( \operatorname {FConv}\left( \operatorname {Transpose}\left( \textbf{X}_{l, intra1}^{i}\right) \right) _{k_i}\right) \end{aligned}$$

(8)

Following the Local Inter Patch Mixer, similar to the Global Patch Mixer, the network employs another Intra Patch Mixer again to fuse the independently processed frequency components, deriving higher predictive feature representations, represented as $\textbf{X}_{l, intra2}^{i}=\operatorname {FLinear}({\textbf{X}}_{l, inter}^{i})$. Subsequently, each patch is transformed back from the frequency ___domain to the time ___domain as $\textbf{X}_{l, time}^{i} = \operatorname {IFFT}\left( \textbf{X}_{l, intra2}^i\right) \in \mathbb {R}^{P_i \times D_i}$. After flattening, the output of this layer is represented as $\textbf{X}_{l}^{i} = \operatorname {Flatten}(\textbf{X}_{l, time}^{i}) \in \mathbb {R}^{L}$.

This design allows the Local Patch Mixer to effectively capture short-term variations and local patterns in time series. Working in conjunction with the Global Patch Mixer, it provides a comprehensive and detailed feature representation for time series forecasting. The features output from these two modules are then aggregated in the Prediction Head for subsequent forecasting.

Prediction head

After obtaining deep representations of historical time series data through the Dual Branch Extractor Block, we transform the temporal representations from both Global and Local branches into the frequency ___domain. We first apply a frequency-___domain linear layer to map the historical window to the future window in the frequency ___domain, followed by an IFFT transformation to return to the time ___domain, generating prediction results.

$$\begin{aligned} \hat{Y}_{g}^{i} =\operatorname {IFFT}\left( \operatorname {FLinear}\left( \operatorname {FFT}\left( X_{g}^{i}\right) \right) \right) \end{aligned}$$

(9)

$$\begin{aligned} \hat{Y}_{l}^{i} =\operatorname {IFFT}\left( \operatorname {FLinear}\left( \operatorname {FFT}\left( X_{l}^{i}\right) \right) \right) \end{aligned}$$

(10)

Ultimately, as shown in Eq. 11, we integrate the predictions to form the final output by assigning equal weights of $\frac{1}{2M}$ to both the global and local components at each resolution, ensuring that the sum of all weights equals 1. This guarantees the conservation of energy, ensuring that the forecasting results remain within a reasonable range.

$$\begin{aligned} \hat{Y} = \frac{1}{2M}\sum _{i=1}^{M}\left( \hat{Y}_{g}^{i} + \hat{Y}_{l}^{i} \right) \end{aligned}$$

(11)

ArcTanLoss

In real world scenarios, time series data frequently experiences abrupt fluctuations, usually due to unexpected situations or events. Most time series forecasting models tend to use MSE as the loss function for training. However, the gradient of the MSE increases linearly as the error increases, as illustrated in Fig. 4a, meaning that anomalous data points are assigned a higher weight during model updates, thereby dominating the parameter learning process and possibly leading to model overfitting on these outliers. This process could diminish the model’s accuracy in predicting regular data trends. Compared to MSE, MAE provides a uniform gradient for all data points as illustrated in Fig. 4b, somewhat mitigating overfitting on anomalies. Nonetheless, even with small deviations, the gradient produced by MAE remains constant, possibly causing the model to oscillate around local minima during optimization, making it challenging to obtain accurate predictions.

To overcome the limitations of traditional loss functions, we innovated from the perspective of the loss function’s gradient. We observed that the function $y' = \arctan (x)$, where $x=e=y-\hat{y}$ represents the error between actual and predicted values, and $y'$ denotes the gradient of the loss function, exhibits the following characteristics:

Adaptive Gradient Value. As x increases, the growth rate of $\arctan (x)$ gradually slows down, leading to a more tempered increase in gradient for large prediction errors, thus avoiding potential drastic fluctuations during parameter updates.
Bounded Gradient. The range of $\arctan (x)$ is between $-\frac{\pi }{2}$ and $\frac{\pi }{2}$, which means the gradient $y'$ is constrained within this range regardless of the value of x. This property provides an inherent stability mechanism for the model training process, preventing gradient explosion issues.
Robustness to Outliers. Due to its gentle growth with large input values, it naturally reduces the disturbance of outliers on model training. This not only helps the model pay more attention to the main trends in the data but enhances the model’s sensitivity to minor fluctuations in the data, thereby improving prediction accuracy.

The $\arctan$ function is particularly well-suited as the gradient of a loss function for time series prediction tasks, especially in cases with outliers or significant amounts of noise. Therefore, as illustrated Fig. 4c, we propose an innovative loss function derived from a transformation of the $\arctan (x)$ function, $y'=a \arctan (kx)$, with its antiderivative calculated as

$$\begin{aligned} \begin{aligned} y&= \int {a\arctan (kx)\textrm{d}x} \\&= -\frac{a}{2k}\ln \left( k^{2}x^{2}+1\right) +ax\arctan \left( kx\right) \end{aligned} \end{aligned}$$

(12)

Furthermore, considering that MAE is a crucial metric for evaluating predictive performance and exhibits insensitivity to outliers, we have integrated MAE into our loss function. Additionally, given the normalization process in data preprocessing, we introduce a constraint on the sum of squared predicted values to optimize the model’s performance on normalized data, ensuring predictions align closely with a zero mean. Collectively, our designed loss function is specifically defined as:

$$\begin{aligned} \begin{aligned} \operatorname {ArcTanLoss}(Y, \hat{Y}) = \sum _{t=1}^{T} \Bigg \{&\alpha \Bigg [ -\frac{a}{2k}\ln \left( k^{2}(y_t-\hat{y}_t)^2 + 1\right) \\&+ a(y_t-\hat{y}_t)\arctan \left( k(y_t-\hat{y}_t)\right) \Bigg ] \\&+ \beta |y_t-\hat{y}_t| + \gamma |\hat{y}_t|^2 \Bigg \} \end{aligned} \end{aligned}$$

(13)

It aims to enhance the overall predictive performance of the model, especially when dealing with complex datasets characterized by noise and outliers. The loss function focuses not only on the fundamental prediction accuracy but also improves handling of outliers, while the squared predicted value constraint ensures consistency and stability in the model’s output.

Experiments

Datasets

To verify the effectiveness of FreMixer, we conducted extensive experiments on seven real-world public datasets²⁷, including Traffic, Electricity, Weather, and 4 Electricity Transformer Temperature (ETT) datasets (ETTh1 & ETTh2, ETTm1 & ETTm2). The detailed attributes of these datasets are as follows.

ETT consists of four subsets, which include two hourly datasets (ETTh1 and ETTh2) and two datasets collected every 15 minutes (ETTm1 and ETTm2). These datasets meticulously record seven key metrics, including the oil temperature and six power load variables of electricity transformers, over the period from July 2016 to June 2018.
Weather compiles 21 meteorological indicators, including air temperature and visibility. These data were recorded every 10 minutes in Germany throughout the year of 2020.
Electricity documents the hourly electricity consumption of 321 customers spanning two years, from July 1, 2016, to July 2, 2018.
Traffic records hourly road occupancy rates measured by 862 sensors on highways in the San Francisco Bay Area from 2016 to 2018.

In our study, we employed the same data preprocessing methods as those typically used in other long-term time series forecasting methods. Specifically, we divided the four ETT datasets into training, validation, and test sets in a 6:2:2 ratio, while the other datasets were split in a 7:1:2 ratio. In Table 2, we provide a detailed description of the dataset, including the number of variates, time steps, and granularity.

Table 2 The properties of the datasets.

Full size table

Baseline models

To comprehensively demonstrate the effectiveness of our model, we compared FreMixer against several state-of-the-art (SOTA) and representative methods, including the following categories: 1) Frequency-based models: FITS¹³, FiLM³⁵; 2) Transformer-based models: PatchTST¹⁷, Autoformer²⁷; 3) MLP-based models: TSMixer³², DLinear²⁹; 4) CNN-based models: MICN²⁴, TimesNet¹⁴; 5) RNN-based model: LSTM²². The corresponding details are introduced as follows:

FITS¹³: A Frequency-___domain model that operates on the principle that time series can be manipulated through interpolation in the complex frequency ___domain, achieving performance comparable to state-of-the-art models for time series forecasting.
FiLM³⁵: A Frequency-Improved Legendre Memory Model designed to preserve historical information in neural networks effectively, while simultaneously minimizing overfitting to noise within historical data.
PatchTST¹⁷: A Transformer-based model that segments time series data into small patches, which not only reduces computational complexity but effectively captures local patterns, thereby enhancing the model’s forecasting accuracy.
Autoformer²⁷: A Transformer-based model replaces self-attention mechanisms with FFT-based auto-correlation operations for series-level modeling to capture periodic dependencies.
TSMixer³²: A Linear-based model that uses MLPs to efficiently extract information by applying mixing operations along both the time and feature dimensions.
DLinear²⁹: A Linear-based model with a single fully connected layer that surpasses most transformer-based methods.
MICN²⁴: A CNN-based model using downsampling convolution and isometric convolution to extract local features and global correlations, respectively.
TimesNet¹⁴: A CNN-based model using FFT to extract periodicity expands the time series from one-dimensional space to two-dimensional space, allowing CNNs to capture intra-period and inter-period variations.
LSTM²²: An RNN-based model that uses memory cells and gating mechanisms to capture dependencies in sequential data.

Implementation details

To ensure the fairness of our work, we adopted the parameter configurations specified in the baseline models’ original publications. Performance evaluations were conducted using two established metrics: MSE and MAE. The length of the input lookback window for the models was selected from $L =\{96, 192, 336, 720\}$. We set $M=2$, with $D_1$ and $D_2$ set to 24 and 72, respectively, by default. The default hyperparameters for ArcTanLoss were configured as $a=1.1$, $k=1.3$, $\alpha =0.5$, $\beta =0.5$, and $\gamma =0.05$. We utilized the ADAM optimizer⁴² with an initial learning rate of 1e-3 and a batch size of 32. An early stopping strategy was employed, ceasing training if no reduction in validation loss was observed over five training epochs. Our models were implemented using PyTorch and trained on an NVIDIA GeForce RTX 3090 24GB GPU.

Main results

Table 3 showcases our forecasting results across seven datasets, with the best and second-best results highlighted in bold and italics, respectively. The datasets were standardized with consistent prediction intervals, designated as $T=\{96, 192, 336, 720\}$. Clearly, FreMixer consistently outperforms in the majority of configurations. Specifically, FreMixer secures a top-two ranking in 54 out of 56 evaluation metrics across various scenarios, with 46 of those achieving first place. Quantitative analysis reveals that FreMixer significantly reduces the MSE by an average of 7.8% and MAE by 7.3% compared to Frequency-based models. When benchmarked against Transformer-based models, the reductions are more pronounced, with an average decrease of 18.8% in MSE and 14.8% in MAE. When compared to Linear-based models, FreMixer achieves reductions of 5.9% in MSE and 6.3% in MAE. In comparison to CNN-based models, FreMixer shows reductions of 22.9% in MSE and 15.3% in MAE. Compared to the RNN-based model LSTM, FreMixer exhibits a dramatic reduction of 78.6% in MSE and 60.7% in MAE. The experimental results demonstrate that FreMixer significantly outperforms all other baselines, including the current SOTA model, PatchTST. While processing the large-scale Electricity and Traffic datasets, which contain over 300 and 800 channels respectively, FreMixer did not exhibit a significant performance advantage compared to PatchTST. We condense the issue to the relatively smaller model capacity of FreMixer. However, even with notably fewer parameters than PatchTST, FreMixer maintained a competitive level of performance. Consequently, the observed performance disparity is considered acceptable. We provide a detailed discussion of these models’ efficiency differences in a later subsection.

Table 3 Multivariate long-term forecasting results.

Full size table

It is particularly noteworthy that FreMixer exhibits good performance even for datasets with low periodicity on the Weather dataset. This underscores the adeptness of our frequency ___domain model in apprehending the global trends within time series data. The model’s proficiency in discerning these overarching patterns, despite the inherent irregularity of the dataset, demonstrates its robust analytical capabilities. In summary, the FreMixer model has demonstrated outstanding performance across multiple datasets and various prediction configurations. These excellent results indicate that our proposed FreMixer is a powerful and competitive model, capable of effectively capturing the dynamic characteristics of time series data and providing accurate predictions, making it suitable for a variety of practical application scenarios.

Ablation study

FreMixer has three key components: the Multi Resolution Segmentation Block, the Dual Branch Extractor Block, and the ArcTanLoss. We conducted extensive ablation experiments to thoroughly evaluate the effectiveness of the proposed method.