Introduction

Cities are complex socio-ecological systems shaped by human activity. As urbanization accelerates, the growing disconnect between social and natural systems has led to an increase in natural, technological, and human-induced disasters. These frequent events pose serious threats to the sustainable development of urban areas, which are characterized by dense populations and concentrated assets. As a result, developing resilient urban systems and improving disaster preparedness has become an urgent priority for both researchers and practitioners. Communities serve as the basic units of urban management and are the foundation for building resilient cities. Among them, urban old communities stand out due to their early construction, distinctive demographics, building styles, and spatial layouts. These factors contribute to specific challenges in disaster management, including limited disaster preparedness, unique geographical constraints, historical value, and vital social functions. On one hand, these features make urban old communities more vulnerable to risks and less capable of responding to disasters. On the other hand, complete redevelopment is often impractical—these areas are typically located in city centers, have continuous occupancy, and remain functionally useful. Redevelopment also entails high costs and potential environmental harm. Therefore, enhancing the disaster resilience of urban old communities within their existing structures is a practical and meaningful direction for research, aimed at improving their capacity for disaster response and recovery.

To date, scholars have made significant progress in studying community resilience, including analyses of resilience mechanisms1,2,3, development of evaluation index systems4,5,6,7, and exploration of enhancement pathways8,9,10,11,12. However, existing approaches often face challenges in accurately assessing disaster resilience in urban old communities due to their complex spatial structures, aging infrastructure, and diverse populations. Traditional assessment models, such as the Analytic Hierarchy Process (AHP) and Fuzzy Comprehensive Evaluation (FCE)13, are widely used but rely heavily on expert judgment, which introduces subjectivity and often lacks dynamic adaptability. The theory of Complex Adaptive Systems (CAS), first introduced by Holland14 and further developed by Holling and Walker15, offers a promising framework for understanding community resilience by emphasizing the nonlinear interactions and self-organizing behaviors of system components. In the field of disaster resilience, CAS theory has been applied to explore the adaptive mechanisms of urban systems under stress. For instance, Zhang et al.16 analyzed disaster response in urban environments through CAS principles; Shang et al.17 highlighted the role of CAS in revealing dynamic urban adaptation; and Zhou et al.18 extended CAS theory to the community level, proposing resilience strategies based on internal feedback loops. However, most of these studies remain conceptual or qualitative, lacking robust quantitative frameworks or dynamic simulation, especially at the community scale. Moreover, the practical application of CAS theory is constrained by difficulties in obtaining comprehensive community-level data. To address these limitations, researchers have explored various information-processing models. The cloud model, proposed by Li Deyi, has been widely adopted to handle uncertainty and fuzziness in environmental management, risk assessment, and decision-making19. While cloud models effectively address data ambiguity, they are rarely integrated with CAS frameworks in the context of urban old communities, limiting their applicability in resilience assessments that require both dynamic and uncertain data handling. Given the irreversible nature of disasters and the scarcity of resources, it is critical to identify key influencing factors and predict resilience evolution trends for targeted resource allocation. In this regard, the Fuzzy Cognitive Map (FCM) model offers high flexibility and interpretability, capable of simulating causal relationships and feedback mechanisms in complex systems20. FCM has been applied in various fields, but its use in disaster resilience research, especially in simulating scenario-based resilience evolution, remains underdeveloped.

Despite the individual strengths of CAS theory, the cloud model, and FCM, existing literature rarely integrates these methods into a unified framework for assessing disaster resilience in urban old communities. This study addresses this gap by combining these approaches to leverage their complementary strengths: CAS theory for system-level analysis, the cloud model for uncertainty management, and FCM for dynamic simulation. This integrated method offers a more comprehensive and adaptive assessment framework, which is both theoretically grounded and practically applicable.

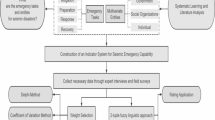
Methods

Construction of the CAS-based resilience evaluation system for old communities

Resilience has evolved through three stages: engineering resilience, which emphasizes rapid recovery to equilibrium21; ecological resilience, which acknowledges multiple equilibrium states and system evolution22,23; and evolutionary resilience, which focuses on continuous adaptation and innovation24,25. In disaster risk management and urban planning, resilience is defined as the ability of systems to absorb disturbances while maintaining core functions, self-organizing, and adapting to change26,27. Based on these perspectives, this study defines disaster resilience in aging urban communities as their capacity to adjust, adapt, learn, and innovate to sustain essential functions and recover effectively from disasters. Identifying resilience structures and assessing their current state are crucial for building a comprehensive resilience framework for old urban communities.

Complex Adaptive System (CAS) theory, introduced by John Holland (1994), explains system evolution as emerging from interactions among adaptive agents14. Communities, as CAS, consist of residents, organizations, and infrastructures that dynamically interact to maintain stability in the face of disasters28. These interactions exhibit nonlinear, coordinated, and evolving dynamics, enabling learning, adaptation, and improvement. This study develops a CAS-based model for old urban communities to analyze disaster resilience resource systems, aiming to enhance their resilience efficiently and provide a theoretical and practical framework tailored to their unique conditions (as shown in Fig. 1).

Fig. 1
figure 1

CAS framework for disaster resilience in old communities.

Full size image

The outer ring represents the major risks faced by old communities. The middle ring highlights the six key resilience dimensions that shape disaster resilience. At the center, individuals, groups, organizations, and other stakeholders interact through dynamic feedback loops, adapting to evolving risks. The arrows illustrate the interconnections and adaptive processes, reflecting the complex and evolving nature of disaster resilience in urban old communities.

Community members serve as the fundamental adaptive agents within a community system. The resources and attributes they possess, including material, economic, cultural, organizational, ecological, and structural aspects, and their interactions collectively form the resilience resource system of the community. Moreover, the dynamism, learning ability, adaptability, and innovativeness of community members drive the development and enhancement of this resource system. In China, traditional disaster risk reduction research often focuses on urban-scale analyses or examines specific aspects of resilience resources in isolation. This approach overlooks the micro-scale perspective of communities and the intricate interrelationships within community resilience systems29. As illustrated by the complex adaptive system model for old communities, the disaster resilience of such communities arises from the synergy of resources carried by adaptive agents. Accordingly, this study examines the disaster resilience of old communities across six dimensions: built infrastructure resilience30, ecological environment resilience31, member composition resilience32, economic condition resilience33, organizational and institutional resilience34,35 and cultural awareness resilience36 (as shown in Table 1).

Table 1 Evaluation index system for disaster resilience of old community.
Full size table

Cloud model

Based on practical experience, the evaluation of the resilience level of old communities is a fuzzy, qualitative judgment rather than an absolute, rigid classification into levels. Therefore, traditional evaluation methods are insufficient for providing a continuous and holistic assessment of the resilience level of old communities. To address the uncertainty between qualitative judgments and quantitative data, a cloud model theory was proposed and continuously refined by experts and scholars led by Academician Li Deyi. The cloud model represents linguistic values, using three numerical characteristics of the cloud (Ex, En, He) to express the mathematical properties of linguistic values.

Among them, the expectation (Ex) represents the expected level of cloud droplets’ distribution in the ___domain space. It is the point that contributes most when describing qualitative concepts in the numerical space. The entropy (En) on one hand represents the measurable granularity of qualitative concepts: the larger the entropy, the larger the granularity, which can be used for granularity calculation to reflect the uncertainty of qualitative concepts. On the other hand, entropy also represents the range of values in the ___domain space that can be accepted by qualitative concepts, i.e., the fuzziness, which is a measure of the “this or that” nature of the qualitative concept. The hyper-entropy (He) is the entropy of entropy, used to measure the change of the uncertainty state, reflecting the thickness of the cloud droplets.

The basic implementation algorithm of the cloud model consists of a forward cloud generator and a reverse cloud generator. On one hand, the reverse cloud generator is used to calculate the cloud’s numerical characteristics with a certain number of precise values, achieving a mapping from quantitative to qualitative. On the other hand, by inputting the three numerical characteristics of the cloud model, the forward cloud generator generates a certain number of cloud droplets, thus realizing the quantitative expression of qualitative concepts. The effective combination of the forward and reverse cloud generators allows for the effective conversion between qualitative and quantitative, considering randomness and fuzziness, as well as the correlation between them. This provides an objective and effective qualitative definition of the evaluation object19.

Entropy weight method

Since the evaluation of the resilience of old communities involves numerous first-level, second-level, and third-level indicators, each indicator contributes differently to the community’s disaster resilience capability. Therefore, when comprehensively considering the overall disaster resilience level of old communities, it is necessary to assign weights to the indicator values based on the contribution of each indicator.

Common methods for assigning weights include subjective weighting methods such as the Analytic Hierarchy Process (AHP), Grey System Theory, and Fuzzy Comprehensive Evaluation, as well as objective weighting methods such as Principal Component Analysis (PCA) and Entropy Weight Method. To effectively ensure the objectivity and scientific accuracy of indicator weighting, this paper adopts the entropy weight method to determine the weights of various indicators at different levels of disaster resilience for old communities. The entropy weight method is widely used in multi-criteria decision analysis as it quantitatively evaluates the amount of information contained in each indicator and assigns weights accordingly. A higher entropy value indicates greater uncertainty in an indicator, resulting in a lower weight, while a lower entropy value corresponds to a more deterministic indicator, receiving a higher weight. The entropy-weight calculation process consists of the following steps:

Step 1 Normalization of Raw Data

Before entropy calculation, all indicator values are normalized to eliminate differences in scale and ensure comparability. Given the diversity of indicators (some being positively correlated with resilience and others negatively correlated), we apply the min-max normalization technique, defined as follows:

  • For positive indicators (higher values indicate better resilience):

$$X_{ij}^{\prime } = \frac{{X_{ij} - \min (X_{j} )}}{{\max (X_{j} ) - \min (X_{j} )}}$$
(1)

  • For negative indicators (higher values indicate worse resilience):

$$X_{ij}^{\prime } = \frac{{\max (X_{j} ) - X_{ij} }}{{\max (X_{j} ) - \min (X_{j} )}}$$
(2)

where \(X_{ij}\) represents the original value of the j-th indicator for the i-th community, and \(X_{ij}^{\prime }\) represents the normalized value.

Step 2 Entropy calculation

The entropy of the j-th indicator is computed as follows:

$$e_{j} = - k\sum\limits_{i = 1}^{n} {p_{ij} } \ln (p_{ij} )$$
(3)

where \(k = \frac{1}{\ln (n)}\) is a scaling constant, \(p_{ij}\) represents the proportion of the i-th community’s value for the j-th indicator, calculated as:

$$p_{ij} = \frac{{X_{ij}^{\prime } }}{{\sum\nolimits_{i = 1}^{n} {X_{ij}^{\prime } } }}$$
(4)

Step 3 Determination of Indicator Weights

The weight of each indicator is determined based on the entropy value:

$$w_{j} = \frac{{1 - e_{j} }}{{\sum\nolimits_{j = 1}^{m} {(1 - e_{j} )} }}$$
(5)

where \(w_{j}\) represents the weight of the j-th indicator, and \(e_{j}\) is its entropy value. A lower entropy value corresponds to a higher weight, signifying greater importance in the assessment.

Evaluation model based on entropy weight method and normal cloud model

This study combines the advantages of the entropy weight method and the normal cloud model to construct a resilience evaluation model for old communities. The detailed steps are as follows:

Step 1 Establish the evaluation factor ___domain \(T = \{ t_{1} ,t_{2} , \ldots ,t_{n} \}\) and the rating ___domain \(V = \{ v_{1} ,v_{2} , \ldots ,v_{n} \}\).

Step 2 Calculate the indicator weights \(W = \{ w_{1} ,w_{2} , \ldots ,w_{n} \}\) using the entropy weight method.

Step 3 Perform single-factor evaluation between the evaluation factor ___domain \(T\) and the rating ___domain \(V\), and construct the fuzzy relationship matrix \(R\).

Step 4 Use the weight set \(W\) and the membership matrix \(R\) for fuzzy transformation to obtain the fuzzy subset \(B\) on the rating ___domain \(V\).

$$B = WR = (b_{1} ,b_{2} , \ldots ,b_{n} )$$
(6)

Here, \(b_{j} (j = 1,2, \ldots ,m)\) represents the membership degree of the evaluated object to the j-th rating. Finally, according to the principle of maximum membership degree, the i-th evaluation grade corresponding to the maximum membership is selected as the most comprehensive evaluation result.

Fuzzy cognitive map

Traditional fuzzy cognitive map

The Fuzzy Cognitive Map (FCM), proposed by Professor Bart Kosko32, is a weighted directed graph constructed based on fuzzy logic and cognitive mapping. It consists of nodes, arcs, and weights, and is used to describe the causal relationships between various factors within a system. By employing fuzzy inference rules, it represents multi-party, feedback-driven dynamic causal relationships. This method can scientifically predict the developmental trends of a system, identify key influencing factors of system changes, and perform simulation analysis of system development under different scenarios. It has been widely applied in complex system modeling31,33. The adaptive disaster resilience of urban old communities under the Complex Adaptive System (CAS) framework involves numerous influencing factors with intricate interrelations. These relationships are further characterized by significant uncertainty. FCM effectively addresses such uncertainties and ambiguities, models the complex causal relationships and pathways within the system, and accurately reflects the nonlinear relationships among factors as well as the dynamic evolutionary processes of the system20,45,46.

The Fuzzy Cognitive Map performs iterations on the initial input data to simulate and predict the future states of the system based on the state values of concept nodes at different time steps and the relationships between nodes. Specifically, using the state values of concept nodes at \(t\) time and their interrelations, the state values at time \(t + 1\) are calculated.

Let \(A_{i}^{t}\) and \(A_{i}^{t + 1}\) represent the state values of concept node \(c_{i}\) at time \(t\) and \(t + 1\), respectively, and let \(w_{ji}\) represent the influence of node \(c_{j}\) on node \(c_{i}\). Then, the state value of concept node \(c_{i}\) at time \(t + 1\) is jointly influenced by the state values at time \(t\) and the effects of other nodes on it, which can be expressed as:

$$A_{i}^{t + 1} = f\left(A_{i}^{t} + \sum\limits_{j = 1,j \ne i}^{n} {A_{j}^{t} } w_{ji} \right)$$
(7)

To map the values of concept nodes to the range [0,1], an S-shaped sigmoid function is typically selected as the threshold function, expressed as:

$$f(x) = \frac{1}{{1 + e^{ - x} }}$$
(8)

The iteration process stops when the state values stabilize at a fixed point or enter a finite cycle, at which point the system’s future development trend under the current conditions can be determined. The stopping criteria for the algorithm require simultaneous satisfaction of two conditions:

  1. a.

    Maximization of the difference between the output values representing the system’s final state and their mean value, ensuring significant divergence among the final state outputs.

  2. b.

    Minimization of the difference between the system’s output values at consecutive time steps, ensuring that the system reaches a steady state or periodic behavior.

Improved fuzzy cognitive map

The construction of traditional fuzzy cognitive map is based on an adjacency matrix, which lacks consideration of indirect relationships among indicator nodes, thereby limiting the comprehensiveness of the model. The DEMATEL method—a system factor analysis approach grounded in graph theory and matrix theory—constructs a direct influence matrix based on logical relationships among system factors, and calculates both the influence exerted by each factor and the degree to which it is influenced by others. This enables systematic and nonlinear analysis of the factors47. Therefore, this study incorporates the DEMATEL method to construct the initial adjacency matrix for the FCM.

The steps of the improved fuzzy cognitive map model are as follows:

Step 1 Construction of the Initial Direct Influence Matrix

In DEMATEL, the construction of the direct influence matrix is often based on extensive expert questionnaires, which introduces a high degree of subjectivity. To address this, our study utilizes the results of the cloud model to evaluate the influence relationships among indicators. Specifically, based on the preceding analysis of influencing factors, mutual influence among secondary indicators in the disaster resilience evaluation system for urban old communities is assessed using the following scale:

“No influence—0, Very low influence—1, Low influence—2, High influence—3, Very high influence—4.”

The resulting matrix is then processed through triangular fuzzy number transformation and defuzzification, which enhances the model’s ability to describe uncertainty in the influence relationships among factors in the resilience system of urban old communities. The final output is the direct influence matrix \(W_{1} = \left[ {w_{1ij} } \right]_{n \times n}.\) Where \(W_{1}\) is a non-negative matrix, \(w_{1ij}\) enotes the degree of direct influence of factor \(c_{i}\) on \(c_{j}\), and \(w_{1ij} = 0\) when \(i = j\).

Step 2 Calculate the normalization matrix \(W_{2}\):

$$W_{2} = s \times W_{1}$$
(9)

where \(s\) is the reciprocal of the maximum value of the sum of the elements of each row in \(W_{1}\).

Step 3 Calculate the full relationship matrix \(W_{3}\):

$$W_{3} = \left( {w_{3ij} } \right)_{n \times n} = W_{2} \times \left( {I - W_{2} } \right)^{ - 1}$$
(10)

where \(I\) is the unit matrix and \(\left( {I - W_{2} } \right)^{ - 1}\) is the inverse matrix of \(I - W_{2}\).

Step 4 Determination of the Initial Adjacency Matrix \(W_{4}\).

The total relation matrix \(W_{3}\) is modified as follows: First, values smaller than the self-influence of each indicator are eliminated. Then, the influence weights and directions of each indicator on the disaster resilience of urban old communities are incorporated. After this adjustment, the initial adjacency matrix \(W_{4}\) is obtained.

Step 5 Obtaining the Optimal Weight Matrix \(W_{5}\).

To further address the fuzziness and complexity introduced by linguistic variables and to enhance the validity and reliability of the weight matrix, this study applies the Nonlinear Hebbian Learning (NHL) algorithm to iteratively optimize the initial adjacency matrix \(W_{4}\), thereby obtaining the optimal weight matrix \(W_{5}\).

Step 6 Establishing the Fuzzy Cognitive Map

To visually represent the interrelationships among the indicators, a fuzzy cognitive map model of community disaster resilience is constructed based on the optimal weight matrix \(W_{5}\).

Study area and data sources

Study area

Old urban communities, commonly constructed in China during the last century through government or state-owned enterprise funding, represent a critical yet underexplored area in disaster resilience research. These communities differ significantly from modern residential areas in terms of infrastructure conditions, demographic composition, and governance mechanisms, making them highly susceptible to various disasters.

  • High Vulnerability and Weak Disaster Resilience

Unlike newly developed urban areas, old communities suffer from aging buildings, poor infrastructure, and inadequate disaster prevention planning. Many buildings were constructed before modern seismic standards, making them more prone to structural failure in earthquakes or other hazards. Additionally, poor drainage and outdated utility systems increase the risks of flooding and fire hazards.

  • Demographic and Social Challenges

Old urban communities often have a high proportion of elderly residents, unemployed individuals, and transient populations, which weakens social cohesion and disaster preparedness. The lack of organized community management further hampers emergency response capabilities.

  • Policy and Urban Development Trends

With rapid urbanization, the redevelopment of old communities faces significant financial and logistical challenges. Governments prioritize urban renewal and disaster mitigation in these areas, but complete reconstruction is often infeasible due to historical value, cost constraints, and displacement concerns. Therefore, enhancing disaster resilience within the existing framework is a more practical and urgent solution.

Taiyuan is a key central city in China’s midland region, with a permanent population of 5.435 million as of the end of 2022. With the continuous development of the city, old communities are increasingly facing prominent issues such as “early construction periods, lack of maintenance and management, significant infrastructure deficits, and high disaster risks.” This study focuses on old communities in Taiyuan, defining those within the research scope based on factors such as building construction age, structural characteristics, spatial planning, functional zoning, infrastructure conditions, and the integration of disaster prevention and mitigation concepts. Specifically, the criteria for inclusion are as follows:

Building Age: 20 to 30 years old.

Building Structure: Brick-wood or brick-concrete construction.

Spatial Planning: Simplistic layouts with unclear functional zoning.

Infrastructure: Outdated facilities with insufficient integration of disaster prevention and mitigation concepts.

Value: Communities located in strategic geographical positions with significant social functional value and considerable potential for continued utilization.

Data sources

Based on the disaster resilience assessment model for old communities, this study selected 56 old communities within the urban area of Taiyuan as samples. All methods were carried out in accordance with the ethical standards and guidelines applicable to social science research. The study protocol, including data collection and participant consent procedures, was specifically designed to comply with China’s Personal Information Protection Law and relevant international ethical guidelines for social science research. Prior to distribution, the study protocol was reviewed and approved by Taiyuan University of Technology Disaster Risk Management Center. Written informed consent was obtained from all participants before data collection. To ensure confidentiality, all questionnaires were anonymized, and participants were explicitly informed that their responses would be used solely for academic research purposes. To further reduce self-reporting bias, the questionnaire avoided leading questions and used neutral language to frame all items. First-hand data on resilience capacity building were collected through community visits and resident interviews. A total of 709 questionnaires were distributed, with 680 valid responses received, yielding an effective response rate of 96%.

Descriptive statistical analysis results are presented in Table 2. The analysis indicates a relatively balanced gender distribution, with a higher proportion of male respondents. The age distribution is dispersed, with the largest group being 36–45 years old (32.06%), followed by 46–55 years old (22.06%) and 26–35 years old (21.32%). In terms of educational background, the majority of respondents hold at least a college degree, accounting for 77.06%. Regarding respondent categories, the sample covers a broad range of stakeholders, with community residents as the largest group (41.76%), followed by community committee staff (15.15%), property management personnel (13.97%), and subdistrict office staff (8.68%).

Table 2 Descriptive analysis statistics.
Full size table

Cronbach’s α reliability coefficient tests were conducted using SPSS 24.0. The results indicate that the overall α reliability coefficient for the indicators is 0.813, and the α reliability coefficients for each dimension are all above 0.7, suggesting good internal consistency among the data (see Table 3 for details)

Table 3 Reliability statistics.
Full size table

Results

Disaster resilience assessment of old communities

Based on literature review and practical considerations, this study classifies the disaster resilience development levels of old communities into five grades:

Grade I: Indicates a high level of disaster resilience in old communities.

Grade II: Indicates a relatively high level of disaster resilience.

Grade III: Represents a moderate level of disaster resilience.

Grade IV: Indicates a relatively low level of disaster resilience.

Grade V: Indicates a low level of disaster resilience.

The specific grade intervals for the evaluation indicators are as follows: Grade I [4, 5], Grade II [3, 4), Grade III [2, 3), Grade IV [1, 2), Grade V [0, 1).

Using MATLAB 2014a as the statistical analysis tool, data from 56 sample communities with 57 variable indicators were input for processing. The entropy weight method was used to calculate the weight of each evaluation indicator, and the cloud model was applied to compute the membership degree of the comprehensive resilience level for each community. The weights for the evaluation indicators at each level are as follows:

First-Level Indicator Weights (\(w_{1}\)):

$$w_{1} = (0.{2828}, \, 0.{1262}, \, 0.{1}0{63}, \, 0.{1221}, \, 0.{1453}, \, 0.{2172})$$

Second-Level Indicator Weights (\(w_{2}\)):

$$\begin{aligned} w_{2} = & (0.0602,0.0896,0.1330,0.0843,0.0420,0.0828,0.0235,0.0253,0.0969,0.0820, \\ & \quad 0.0633,0.0327,0.0935,0.0482,0.0428) \\ \end{aligned}$$

Third-Level Indicator Weights (\(w_{3}\)):

\(\begin{aligned} w_{3} = & (0.0063,0.0250,0.0067,0.0221,0.0157,0.0103,0.0260,0.0211,0.0164, \\ & 0.0284,0.0169,0.0254,0.0288,0.0127,0.0103,0.0105,0.0166, \\ & 0.0386,0.0185,0.0106,0.0160,0.0100,0.0160,0.0196,0.0397,0.0134, \\ & 0.0100,0.0134,0.0101,0.0067,0.0077,0.0040,0.0068,0.0328,0.0254,0.0102, \\ & 0.0284,0.0231,0.0190,0.0400,0.0215,0.0209,0.0210,0.0079,0.0143,0.0105, \\ & 0.0451,0.0294,0.0191,0.0078,0.0204,0.0107,0.0094,0.0124,0.0129,0.0138,0.0037) \\ \end{aligned}\) 

The comprehensive disaster resilience evaluation results for the communities are presented in Table 4 (only partial community results are shown due to space limitations) and Fig. 2.

Table 4 Evaluation results of disaster resilience of old communities based on entropy weight cloud model.
Full size table
Fig. 2
figure 2

Cloud model restoration map of comprehensive resilience index for communities.

Full size image

According to Table 3 and Fig. 2, the disaster resilience levels of old urban communities are generally low. Among the 56 old communities, 31 fall into the moderately low category, 18 into the relatively low category, and 7 into the low category. Communities with moderately low resilience are mainly located in Xinghualing District, while those with relatively low resilience are concentrated in Wanbailin District. Communities with low resilience are primarily found in the southern region of Yingze Street within Yingze District.

This situation can be partly attributed to the historical development of Taiyuan City. Xinghualing District and the area north of Yingze Street in Yingze District were early-established administrative and financial trade areas, as well as employee housing for major state-owned enterprises in electricity, banking, and railways. These areas generally exhibit more standardized planning, construction, and management. Wanbailin District, on the other hand, began developing in the 1990s into a comprehensive industrial area hosting coal, chemical, machinery, textile, power, construction materials, electronics, pharmaceuticals, and defense industries, forming a national energy-heavy chemical base. Although its residential areas, largely consisting of employee housing, were constructed earlier, their spatial planning is relatively better. Furthermore, the implementation of grid-based management, with a focus on specific sub-districts, has clarified responsibilities for managers, leading to more systematic and thorough oversight.

In contrast, the southern part of Yingze Street in Yingze District, particularly around Qingnian Road No. 1 Community and Bingzhou Road No. 1 Community, faces significant challenges. These include aging buildings, a high density of elderly residents, suspended pipelines, cluttered staircases, narrow spaces between buildings, and severely inadequate parking facilities. Consequently, this area exhibits the lowest disaster resilience levels among the three regions examined.

To further analyze deficiencies in the disaster resilience construction of old communities and explore targeted pathways for improving resilience, this study conducted a detailed analysis of each dimension of community resilience resource systems.

As shown in Fig. 3a–f, the resilience levels across all dimensions of old communities are generally moderately low, with built infrastructure resilience being particularly deficient and in a highly insecure state. This is directly related to the early planning and design of old communities, which inadequately accounted for evacuation spaces and firefighting facilities, lacked comprehensive seismic and disaster-resistance standards, featured non-standard architectural designs, and suffered from aging pipeline networks and insufficient backup systems. In contrast, the resilience of member composition is relatively better. This may be attributed to factors such as low vacancy rates in these older neighborhoods, where most residents have lived for over 10 years. Consequently, there is a high degree of familiarity, recognition, and belonging within the community. Additionally, many residents are retired workers with stable pension incomes, high basic medical coverage, and harmonious neighborhood relations. However, ecological environment resilience, economic condition resilience, organizational and institutional resilience, and cultural and awareness resilience are generally low. This is partly due to inadequate functional zoning considerations in early planning and the high concentration of elderly populations, whose primary income source is their pensions. Furthermore, these challenges are linked to the top-down management approach long prevalent in China, which has resulted in limited dynamism in grassroots management systems and insufficient resident participation.

Fig. 3
figure 3

Resilience cloud model restoration map of various dimensions.

Full size image

Key factors for disaster resilience in old communities

According to the weight assignment results derived from the entropy weight method, the primary dimensions that significantly impact disaster resilience in old communities are built infrastructure resilience (0.2828) and cultural awareness resilience (0.2172). This highlights that built infrastructure serves as the cornerstone for safeguarding lives and property, making the enhancement of built infrastructure resilience an imperative requirement. Under the existing level of built infrastructure, the disaster prevention and mitigation awareness, mutual aid capabilities, and unity and cohesion within the community over a certain period become the key determinants of emergency response capabilities. Other dimensions of resilience resources primarily supplement these foundational capabilities, playing a supporting role in recovery and sustainable development over longer timeframes.

Among the secondary indicators, factors with a notable influence on the disaster resilience of old communities include basic service facilities (0.0896), emergency response capacity (0.1330), community greening (0.0843), residents’ mutual assistance capability (0.0828), community economic resilience (0.0969), standardization of institutional development (0.0820), and the community’s disaster prevention atmosphere (0.0935). The breakdown of secondary indicators indicates that during the sustainable construction of disaster resilience in old communities, overall capabilities and collective awareness are the most critical aspects at the current stage.

At the tertiary indicator level, relatively important indicators include firefighting configurations (0.0250), issues related to illegal constructions (0.0221), road conditions (0.0260) and parking planning (0.0211), disaster information collection (0.0254) and dissemination (0.0284), the construction of shelters (0.0288), availability of green spaces and forests (0.0386), proportion of floating populations (0.0397), investment in disaster reduction funds (0.0328), per capita GDP (0.0254), availability of temporary supplies (0.0284), the establishment of disaster prevention and mitigation regulations (0.0231), emergency planning (0.0400), the development of disaster self-help organizations (0.0215), accessibility to external rescue services (0.0210), community crisis awareness (0.0451), community self-help capabilities (0.0294), emergency material reserves, and residents’ risk perception (0.0204).

Based on the evaluation results and field survey findings, the generally low levels of disaster resilience in urban old communities can be attributed to the following key factors:

  1. (1)

    Severe Deficiencies in Built Infrastructure Resilience

    • Aging Structures with Poor Disaster Resistance Most buildings are decades-old brick-concrete structures with limited resistance to earthquakes and other disasters. Firefighting infrastructure is minimal, relying heavily on external assistance, leaving communities inadequately prepared for emergencies.

    • Outdated Energy Supply Systems Aging pipelines without backup systems are vulnerable to failure. The “tree-branch” urban lifeline layout means disruptions in the main supply can result in prolonged water and electricity outages.

    • Inadequate Parking and Road Infrastructure Lack of designated parking spaces leads to the occupation of pedestrian paths and fire lanes, causing congestion. Non-motorized vehicles often obstruct thoroughfares due to insufficient parking facilities.

    • Insufficient Emergency Shelters and Evacuation RoutesMany communities lack emergency shelters and clearly marked evacuation routes. Narrow, cluttered pathways further impede evacuation efforts.

    • Obsolete Disaster Communication Systems Disaster information dissemination relies on community office screens or bulletin boards, increasing the risk of delays and communication gaps during emergencies.

  2. (2)

    Insufficient Ecological Environment Resilience

    • Low Green Coverage Green coverage typically ranges from 10 to 15%, far below the 40% target. Limited green space and high impervious surface ratios intensify urban heat island effects and increase runoff, straining drainage systems and contributing to waterlogging and “urban flooding.”

    • Weak Micro Water Cycle Infrastructure Inadequate water cycle systems heighten environmental risks and threaten water safety.

    • Hazards from Overhead Utility Lines Exposed utility lines, vulnerable to weathering, pose significant fire and safety hazards, especially when entangled with tree branches.

  3. (3)

    Imbalanced Member Composition Resilience

    • Unique Demographic Characteristics High occupancy rates and long-term residency foster familiarity and community cohesion, which can support disaster response efforts.

    • Challenges from High Rental and Elderly Populations Renters often lack community attachment, while elderly residents face mobility and awareness limitations, reducing participation in disaster preparedness.

    • Dual Risk of Elderly Populations The elderly are not only highly vulnerable during disasters but may also contribute to risk due to limited response capacity.

  4. (4)

    Weak Economic Resilience

    • Lack of Funding and Supplies Community committees report persistent shortages of disaster mitigation funding and emergency supplies, severely limiting self-help and mutual aid capabilities.

  5. (5)

    Inadequate Organizational and Institutional Resilience

    • Overburdened Grid Management Each grid manager oversees 300–400 households, reducing the effectiveness of community governance.

    • Generic and Outdated Emergency Plans Existing disaster plans are often not tailored to specific community needs and lack regular updates.

    • Weak Support Networks Most communities lack resident-led self-help organizations and maintain minimal ties with external volunteer groups, heavily relying on external rescue services.

    • Legacy Governance Issues Communities formerly managed by enterprises struggle with disorganized governance post-corporate restructuring, deterring property management firms from assuming responsibility and further complicating resilience enhancement.

  6. (6)

    Limited Cultural Awareness Resilience

    • Declining Learning Capacity Among Residents An aging population faces difficulties acquiring new knowledge, leading to low risk perception and limited self-help skills.

    • Poor Awareness of Risk Information Residents are generally unaware of how to access or report disaster risks.

    • Bridging the Communication Gap Strengthening resident engagement, raising risk awareness, and fostering self-rescue capabilities are essential for building safer, more resilient communities.

Simulation of disaster resilience enhancement

To comprehensively simulate the evolutionary state of the disaster resilience system in old communities, the weight values derived from the Entropy Weight-Cloud Model evaluation results were used as the basis for constructing the initial adjacency matrix of the Fuzzy Cognitive Map. The mutual influences among factors within the system were also considered. Based on the analysis of influencing factors, the relationships among secondary indicators in the disaster resilience evaluation system were evaluated on a scale of 0 to 4 (no impact to very high impact), resulting in a Direct Impact Matrix. This matrix underwent triangular fuzzy number conversion and defuzzification to better address uncertainties in factor interactions. Subsequently, the matrix was adjusted by removing values smaller than the self-influence of the indicators and incorporating the weight and directional influence of indicators on disaster resilience. This process produced the initial adjacency matrix \(W_{1}\), which was iteratively calculated using formulas (7–10) to derive the optimal weight matrix \(W_{5}\). Finally, based on \(W_{5}\), the Fuzzy Cognitive Map model for disaster resilience in old communities was established, as shown in Fig. 4.

Fig. 4
figure 4

Fuzzy cognitive map constructed based on the optimal weight matrix \(W_{5}\).

Full size image

In this map, each concept represents an individual indicator, and the directed arrows, along with the numerical values on them, indicate the causal influences and the relative strengths between these factors.

By normalizing the expected values of the dimension indices and the overall resilience index from the cloud model evaluation results of disaster resilience in old communities, the initial state of the system is obtained as \(A_{i}^{(0)}\) = (0.3724, 0.4049, 0.3433, 0.4978, 0.3960, 0.5156, 0.5246, 0.6505, 0.3639, 0.4814, 0.3694, 0.5813, 0.4782, 0.4723, 0.4399, 0.4378). Inputting \(W_{5}\) and \(A_{i}^{(0)}\) into the simulation model and iterating 13 times, the system gradually stabilizes. At this point, the steady-state values of the system are \(A_{i}^{(1)}\) = (0.6657, 0.6730, 0.6912, 0.6611, 0.6654, 0.6629, 0.6596, 0.6590, 0.6608, 0.6754, 0.6864, 0.6870, 0.6896, 0.6884, 0.7145, 0.8005), representing the final state of the disaster resilience system in old communities under current conditions (as shown in Fig. 5).

Fig. 5
figure 5

Evolutionary trend of disaster resilience in old communities.

Full size image

To explore the sensitivity of the disaster resilience system in old communities to various influencing factors, six simulation scenarios were set based on the analysis of key factors. Each scenario focuses on enhancing one specific dimension of resilience: (a) built infrastructure resilience, (b) ecological environment resilience, (c) member composition resilience, (d) economic condition resilience, (e) organizational and institutional resilience, and (f) cultural awareness resilience.

In each scenario, secondary indicators under the respective dimension were activated. For instance, in the scenario aimed at improving Built Infrastructure Resilience, indicators such as (a1) safety of housing, (a2) basic service facilities, and (a3) emergency response capability were activated. Since all indicators within the disaster resilience system of old communities are positive indicators, the expected values of the activated indicators were set to 1 during the simulation. These values, along with the optimized matrix \(W_{5}\), were input into the simulation model to analyze the system’s sensitivity under different scenarios when reaching a stable state.

The simulation results (see Table 5) indicate that the disaster resilience levels under all six scenarios have improved to varying degrees. Among them, the most significant improvement in the disaster resilience index (RI) of old communities, amounting to 0.0145, occurred under the scenario of activating built infrastructure resilience (a1 housing safety, a2 basic service facilities, a3 emergency response capability). Similarly, a substantial improvement of 0.0108 was observed under the scenario of activating cultural awareness resilience (f12 community cohesion, f13 community disaster prevention and mitigation construction, f14 residents’ willingness for disaster prevention and mitigation, f15 residents’ disaster response capability).

Table 5 Simulation results for disaster resilience enhancement in old communities.
Full size table

In the scenarios of activating ecological resilience (b4 community greening construction, b5 wastewater and waste disposal capability), economic resilience (d8 residents’ economic resilience, d9 community economic resilience), and organizational resilience (e10 standardization of institutional development, e11 construction of disaster prevention organizations), the RI increased by 0.0070, 0.0076, and 0.0077, respectively, indicating moderate improvements in the disaster resilience levels of old communities.

In contrast, the scenario of activating member composition resilience (c6 community mutual assistance capability, c7 residents’ self-help capability) showed a smaller RI change of 0.0059, reflecting a relatively minor improvement in the disaster resilience level of old communities.

Strategies of disaster resilience enhancement

In light of resource constraints and based on the assessment results of community resilience, this study proposes the following targeted strategies to enhance disaster resilience in urban old communities:

  1. (1)

    Harmonious Living and Green Renovation

Given that residential buildings in old communities were constructed decades ago using outdated methods and fail to meet current seismic and disaster resistance standards, structural reinforcement and renovation are imperative. In accordance with the Interim Regulations on Sponge City Planning and Management issued by the Taiyuan Urban and Rural Planning Bureau (2018), such upgrades should integrate the concept of “harmonious coexistence between humans and nature” and emphasize green, coordinated development. This includes the construction of green buildings, mitigation of excessive impervious surfaces, and promotion of urban micro-circulation systems. In parallel, firefighting facilities in residential buildings should be progressively upgraded. The transition of old communities into formal property management should be accelerated, with standardized emergency supply stockpiles established at the community level. Moreover, improved coordination between community committees and property management companies is essential to address current information fragmentation. By integrating their respective strengths in management and information, a joint prevention and control mechanism can be established to enhance emergency response capacity.

  1. (2)

    Three-Dimensional Planning for Spacious and Orderly Environments

To resolve issues related to road congestion and inadequate parking planning, a comprehensive, multi-dimensional approach is necessary. For motorized vehicles, current plans are insufficient, often encroaching on fire lanes. Constructing multi-level parking structures shared by adjacent communities can alleviate parking shortages, improve road conditions, and enhance residents’ daily mobility. For non-motorized vehicles, designated parking zones and standardized, orderly placement should be implemented to prevent chaotic parking and unauthorized charging setups. These measures will not only improve safety and aesthetics but also strengthen residents’ sense of belonging and satisfaction.

  1. (3)

    Dual Protection with Smart Monitoring

First, establish a “networked” energy supply system that ensures redundancy and complementarity between main and branch lines, guaranteeing continuity in emergency energy provision. Second, develop a “multi-source” supply model through urban micro-circulation systems, ensuring that critical resources such as water and electricity (e.g., via solar panels) remain uninterrupted during supply disruptions. Third, build an intelligent safety monitoring platform by investing in resources and talent to integrate safety oversight with IoT, cloud computing, big data, artificial intelligence, and “Internet+” technologies. This platform will enable real-time perception, accurate risk detection, professional assessment, and coordinated early warnings, ensuring the stable and secure operation of urban lifeline systems through continuous monitoring.

  1. (4)

    Intelligent Platforms for Efficient Communication

To address inefficiencies in disaster information collection and limited communication channels, communities should proactively develop risk distribution maps and evacuation plans, including the identification of vulnerable populations. Residents should be actively involved in hazard identification efforts.

Leveraging intelligent digital tools, a community safety application platform can be developed to enable real-time risk reporting by residents. This not only enhances public risk awareness and participation in disaster resilience efforts but also facilitates more efficient communication between community managers and residents, ultimately improving disaster response efficiency.

  1. (5)

    Strengthening Self-Help Capabilities and Fostering a Resilience Culture

Global experiences in disaster risk reduction underscore the critical role of community residents as the primary force in disaster response. Strengthening community-based self-help systems is essential to compensate for staff shortages. Under the guidance of community workers, resident self-help and mutual aid groups should be established.

In addition, public education campaigns on disaster prevention and mitigation should be intensified, along with training in emergency response skills. Regular emergency drills and resource stockpiling activities should be organized to improve residents’ preparedness, self-help capacities, and evacuation response times, thereby reinforcing overall community resilience.

Discussion

This study proposes an integrated framework for assessing disaster resilience in urban old communities by combining CAS theory, the entropy-weight cloud model, and FCM simulation. This framework captures the dynamic interactions among key resilience factors and quantitatively assesses their impact under various scenarios. By integrating CAS theory with FCM simulation, the study offers a novel perspective on resilience enhancement mechanisms and improves predictive accuracy by simulating the temporal evolution and within community systems.

Compared with traditional resilience assessment models such as the Analytic Hierarchy Process (AHP), Fuzzy Comprehensive Evaluation (FCE), or basic statistical approaches, our method offers several advantages. While AHP and FCE often rely on expert judgment, introducing subjectivity, the entropy-weight method ensures objective, data-driven indicator weighting. Moreover, conventional models typically assess resilience in a static context, failing to capture how resilience evolves over time. In contrast, the integration of FCM enables dynamic simulation of resilience development, reflecting real-world adaptation processes. The tailored application of CAS theory to urban old communities is also relatively rare, enhancing both the originality and contextual relevance of this study.

Simulation results reveal that factors such as built infrastructure and cultural awareness play critical roles in enhancing community resilience. Based on these insights, we propose targeted strategies including infrastructure renovation, space optimization, and improved disaster awareness, implemented in a phased manner due to resource constraints. These strategies are practical, adaptable, and supported by dynamic assessment results, offering actionable guidance for policymakers.

In this study, model validation was primarily conducted through consistency analysis between simulation outputs and established theoretical frameworks, alongside expert validation of the FCM structure and weight matrix. The model’s identification of critical resilience factors aligns with recognized theoretical insights, supporting the reliability of our approach. However, we acknowledge that alternative validation methods, such as cross-validation with other resilience models, could further strengthen the robustness of our framework. Due to contextual constraints, such methods were not implemented in this study. Future research will aim to incorporate these validation techniques and apply the framework to broader case studies, enhancing the model’s generalizability and predictive performance across diverse contexts.