Introduction

Sea ice is a key component of the complex Antarctic climate system and therefore of the global climate system. Its variability is driven by interaction of the atmosphere and ocean on a multiplicity of temporal and spatial scales. Over the period 1979–2016, satellite-observed total Antarctic sea ice extent experienced a small, statistically significant, positive trend supported by record winter maxima in 2012 and 2014. This positive trend is subject to strong regional trends of opposing nature, in particular sea ice decrease in the Bellingshausen-Amundsen Sea. Remarkably, successive record summer minima in February 2017, 2022 and 2023, following the previous winter maxima, have reduced the positive trend to insignificance. While the sea ice extent recovered to normal levels after the 2017 record minimum, it has so far failed to do so after the 2022 record minimum and in 2023 sea ice extent remained at record low levels for the entire year. Moreover, these record low levels have continued into 2024 which saw the second lowest winter maximum of the satellite era1. This highly unusual variability has prompted suggestions of fundamental change in the Antarctic sea ice system2,3 and a discussion of structural change1,4.

Structural change in the Antarctic sea ice record may be defined statistically as a change in its stochastic process, including changes in mean state, variability or persistence. Persistence is a measure of the long term impact of a change (increase or decrease) in SIE on the future values of SIE. A direct measure of persistence is the auto-correlation function of the time series. We use a summary measure of persistence that quantifies the long-term effect of perturbations on SIE5,6 [See Methods]. A change in the mean state of Antarctic sea ice was considered by ref. 1 who used change point analysis to define two change points in the system, 2007 and 2016, thereby separating the observed sea ice record into three parts. Their analysis shows the high mean sea ice extent from 2007 to 2016 and low mean sea ice extent from 2016 to 2023. While they showed a change in the mean state between the two periods, the difference in variability was not statistically significant. The changing variability of the sea ice area in the austral summer was examined by ref. 4 who used the change point year of 2007 identified by ref. 1. They found a statistically significant increase in variance after 2007, compared to the period before, and noted that increased variance and persistence are precursors of a regime shift.

These two studies are based on the relatively short span of satellite-observed data available. The short time span of 44 years limits our ability to assess and understand this apparent change in structure somewhat, making a longer historical record necessary to provide context. Recently, two reconstructions of circumAntarctic sea ice extent have been published7,8. The first7, presented reconstructions of Antarctic sea ice by sector and season for the 20th century. These have proven valuable for helping to understand recent sea ice variability as is discussed below. The second8, presented reconstructions of monthly sea ice extent for the 20th century, based on a reconstruction model which uses the Bayesian statistical framework to create regionalized, stochastic ensembles of Antarctic sea ice [See Methods]. They differ in reconstruction method and temporal resolution. However, they use the same temperature and pressure observations from a network of 30 stations across the Southern Hemisphere along with indices of climate variability extending back to 1905; both reconstructions end in 2020.

Here we present an analysis of the reconstructions, merging it with the satellite-observed data, and placing into context the contemporary variations in Antarctic sea ice. In particular we calculate the probability of the present extremes of sea ice extent occurring in the pre-satellite 20th century. We also address the question of structural change in the sea ice system, focusing on the changing persistence of the sea ice extent anomalies. We present evidence of significant structural change. We also show that the variation in sea ice is more consistent with non-stationary regime evolution over recent time rather than regime shifts.

Results

Twentieth Century Monthly Reconstructions of Antarctic sea ice

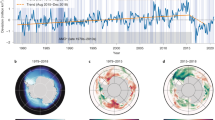
The ensemble reconstruction that we use in our analysis is displayed in Fig. 1 which shows 2500 randomly sampled individual reconstructions of the anomalies from the climatological mean (overplotted in black). The total sea ice extent (SIE) is shown along with the regional SIE in the five sectors defined by ref. 9.

Fig. 1: Ensemble reconstruction of 20th century Antarctic sea ice extent anomalies (1905–September 1978) with satellite observed sea ice extent anomalies (1979–2023), for the total sea ice and for each sector.
figure 1

Individual reconstructions are drawn in light gray—there are 2500 so they appear black; the average of the individual reconstructions in red, and the observed sea ice in blue. As the red curve is the average of 2500 reconstructions it varies much less than the individual reconstructions (black). Our analysis uses the individual reconstructions because they better encompass the range of variation in the sea ice extent. Units are in millions of km2. Note the different scales of the vertical axes.

Full size image

A set of six randomly sampled individual reconstructions of the total sea ice (each an equally likely depiction of a possible evolution of Antarctic SIE in the 20th century) is shown in Supplementary Fig. 1.

We provide here a brief overview of the information shown in the reconstructions. The reported large-scale decline in total SIE over much of the 20th century7, is apparent in Fig. 1, as well as Supplementary Fig. 1. Regionally, it is driven largely by sea ice decline in the Bellingshausen-Amundsen and Weddell Seas. Interestingly for the Weddell Sea, the reconstructed sea ice declines continuously over the course of the 20th Century with only minor sub-decadal fluctuations. In the Bellingshausen-Amundsen Sea (ABS) sector the reconstructions exhibit generally higher SIE than in the satellite period, with a notable increase in sea ice from the late 1940s to the 1970s, preceding the satellite-observed decrease in SIE. This is in contrast to the suggested persistent decreases in this sector over the 20th century10. In the King Haakon VII and East Antarctica sectors there are no major trends in the reconstruction averages, but the variation across the reconstruction ensemble is fairly high, making it impossible to rule out a positive or negative trend, or no trend at all, especially within certain seasons as demonstrated for austral winter7. The Ross-Amundsen Sea sector exhibits lower sea ice levels at the beginning of the 20th century than during the satellite observed period. However, as for the King Haakon VII and East Antarctica sectors, the reconstruction uncertainty, as represented by the variation between individual reconstructions, is large in this sector and almost always encompasses zero, the climatological mean.

Our results in Fig. 1 are qualitatively similar to earlier work7 in that we have non-stationarity induced by the pre-satellite era indices. Our approach employs the underlying assumption that the unobserved past comes from the same process as the satellite observed present. We assume conditional stationarity given the pre-satellite era indices used in the process but not simple stationarity, i.e unconditional on the pre-satellite era indices7.

The trend in reconstructed total sea ice is the area-weighted sum of all trends in all sectors, since the total sea ice is computed as the sum of sea ice in all sectors. These reconstructions suggest that the decline in sea ice over the 20th century was due largely to reductions in the Weddell and Bellingshausen-Amundsen Seas sectors. They also show that the positive trend in satellite-observed SIE began around the time that satellites began recording sea ice observations and according to our reconstructions this was preceded by a negative trend. This outcome at the monthly level is consistent with the seasonal reconstruction reported by ref. 7, who suggested that there was a reversal in Antarctic sea ice trends between the 1960s and 1970s.

The monthly reconstruction of the satellite observations for the 1979–2023 period is exactly equal to what is observed (that is, the blue lines in Fig. 1). This is because the posterior distribution of the satellite observations represents what we can know about what the satellite observations would have been, and we know their values exactly when they are directly observed. However, to assess the fidelity of the reconstructions to the satellite observations we can use the posterior predictive distribution of the satellite observations. This is the (counter-factual) distribution of what the reconstruction model thinks the satellite observations would have been11. We compare draws from the posterior predictive distribution to the satellite observations in Supplementary Fig. 3. If the process that generated the satellite observations is the same as that used in the reconstruction model then the satellite observations should be similar to a predictive reconstruction. That is, the satellite observations should be indistinguishable from ensemble members. In particular its values should be within the range of the ensemble members. While this is generally so prior to 2015, there do appear to be divergences post-2015. The satellite observations and predictive reconstructions have similar monthly variances as is suggested by Supplementary Figs. 1 and 3. Supplementary Table 1 compares the variances of the reconstructions to that of the satellite observations and they are close.

The comparison between the reconstructions and the observed can be seen more clearly in Supplementary Fig. 4. Here we plot the percentile rank of the observed within the distribution of reconstructions. The top (bottom) horizontal red dashed line represents the 95th (5th) percentiles. If the post-2015 satellite observed sea ice extent anomalies are similar to the past, approximately 5% of the post-2015 satellite observed sea ice extent percentiles (green) should be below the bottom red line and approximately 5% above the top red line. For most sectors and the total we see many more extreme lows and fewer extreme highs. This figure shows more clearly the extremities of the recent observations.

We can also quantify the degree of summer persistence versus spring reemergence in the reconstructed sea-ice time series12. Supplementary Figs. 5–7 show correlations between sea ice extent anomalies for each month-of-the-year and each following month-of-the-year. We see that the patterns of predictability are similar and reflect the two predictability patterns seen by others12: persistence from summer initial months with correlations lasting till June and reemergence from spring initial months to the following autumn months.

The large-scale development of reconstructed Antarctic sea ice is summarized in Fig. 2, showing the reconstructed sea ice anomaly over time and month, by sector, in millions of km2. In the total SIE, the positive anomalies at the beginning of the 20th century are strongest in the winters of the 1930s before weakening over the decades and becoming negative in the 1970s, consistent with the negative trend found by others7. There is strong decadal variability in the annual cycle of total SIE with the tendency for both enhanced and reduced amplitudes occurring across the autumn to early spring period, in both the reconstructed and observed data. While this decadal variability is present in each sector, it is strongest in the Weddell Sea and to a lesser extent in East Antarctica. The contemporary positive trend in SIE in the Ross-Amundsen Sea appears to be part of this pre-satellite era decadal scale variation while in the Bellingshausen-Amundsen Sea, SIE was experiencing a positive trend several decades before the turnaround near the start of the satellite era. There is also some evidence of opposing anomalies in the Bellingshausen-Amundsen Sea and Ross-Amundsen Sea sectors, similar to observations which may be tied to variability in the Amundsen Sea Low. The observed reduction in total SIE in recent years is precipitous when seen in the context of the 20th century reconstructions.

Fig. 2: Reconstructed sea ice extent anomaly by month-of-year, year and sector in millions of km2 from 1899 to 2023.
figure 2

The values are the average anomalies over the ensemble of reconstructions. The values from 1979 onward are the satellite-observed sea ice extent anomalies.

Full size image

Supplementary Fig. 2 presents the figure in tabular form, aggregated by decade, and with their standard errors so that variability can be assessed.

Probability of 21st Century Extreme Sea Ice Events

An important question that cannot be answered using the satellite record alone is how extreme events in the satellite record like the 2014–2016 sea ice decline or the February 2017, 2022, and 2023 Antarctic extreme sea ice minima, compare to the pre-satellite sea ice in the earlier part of the 20th century. Our framework allows the estimation of how likely a similar event might have happened, by querying our stochastic ensemble reconstructions on whether or not the event occurred in the reconstruction period. Extreme events like the 2014–2016 sea ice decline are possible to detect in a series like ours because the expected uncertainty of the sea ice extent is estimated and is a property of the reconstructed sea ice extent. Therefore occurrences that fall outside of the expected uncertainty are detectable.

We define the event associated with the 2014-2016 decline in total Antarctic SIE as a difference of 4.18 million km2 or more in a two-year window. This is the difference between the largest positive anomaly of +1.92 million km2 in January 2015 and the largest negative monthly anomaly of −2.26 million km2 in December 2016 observed in this time period. We compute for each of our sea ice reconstructions the maximal difference in sea ice anomaly in a two-year sliding window (see Methods; see Supplementary Fig. 8) and find that only 0.32% of the reconstructions have a difference greater than the observed two-year difference of 4.18 million km2. Our reconstructions therefore suggest the probability of a two-year difference in total Antarctic SIE anomalies of 4.18 million km2 or more to have occurred between 1899 and 1979, is 0.0032 or 0.32%. Further, to adjust for selection bias, over a window sized to match the length of the observed data record (i.e., 44 years) we compute the probability that a two-year drop greater than that observed is even lower, 0.0021 or 0.21%. Thus, the 2014–2016 decline in total Antarctic SIE is extremely unlikely to have happened in the reconstruction period 1899–1979, under the assumption that the sea ice response to atmospheric forcing had not changed. A similar conclusion, but based on seasonal reconstructions using the same predictor data, was reached by earlier work7.

The period of extreme minima in summer was preceded by years (2012, 2014) in which the winter sea ice maximum reached record levels. Using the same method as for the February extreme minima, we computed the probability of them occurring in the pre-satellite era. We found that the probability of the 2012 winter maxima occurring was 97% while that of the 2014 winter maxima was 13%. This indicates that the 2014 maximum approaches an extreme high while the 2012 maximum is not extreme. These probabilities are both visible on Supplementary Fig. 8d.

For each of the extreme February minima (2.36 in 2017, 2.34 in 2022 and 2.04 in 2023; million km2), we check each of our reconstructions to see whether or not a sea ice extent of, or below those values was probable. We identify the lowest sea ice minimum that occurred in a 44-year window for each reconstruction and find that the probability of a February 2017 event was 0.07(7%); that of a February 2022 event was 0.062(6.2%), and that of February 2023 was 0.013(1.3%). Further we find that 16% of all 2500 reconstructions have their lowest SIE of 2.22 million km2 or less, which always occurred in the month of February. Therefore, while extremely uncommon, the reconstructions suggest that the SIE might have previously reached such extremely low values in the pre-satellite 20th century. We further analyzed in which year the lowest February anomaly occurred and find the late 1970s in general and in particular the year 1977 to have unusually low February SIE. The year 1977 has been independently identified as a year of low sea ice in the literature13. Of the reconstructions where a February as extreme or more extreme than the February 2022 minimum occurred, about 26.3% (105/400) are predicted in February 1977. Such extremes were also found with slightly increased probabilities for February 1975 and 1976, but not nearly as likely as 1977. Other probable years are more spread out over the course of the reconstruction period and do not occur in noteworthy clusters.

We also considered the extremity of the winter of 2023. The average sea ice extent for June, July and August was 13.78 million km2. We found the lowest winter average occurring in a 44-year window for each reconstruction and find that none of them had a sea ice extent that low (that is, the probability is less than 0.1%). Note that similarly, CMIP6 models rarely simulate winter sea ice extent as anomalously low as that observed in winter 202314.

The recent Antarctic sea ice variability is marked not only by the extremes themselves but also by the frequency with which they occurred - three record minima within 6 years. For each reconstruction we calculated the probability that within a 44-year window there is a six-year window in which three record minima occur is less than 0.1%. Given that the reconstructions suggest that the extremes that we have observed in the 21st century are highly unlikely to have occurred in the reconstructed pre-satellite 20th century, we ask the question: Has there been a change in the variability of Antarctic sea ice, now detectable in the 21st century?

Structural change in the Antarctic sea ice system

The recent occurrence of extreme sea ice events suggests the possibility that the Antarctic sea ice system has undergone recent change1,4. The sea ice system is complex, and includes factors that influence mean state, variability and the co-variation of SIE. Here we consider two modes of change. One is a regime shift, in the sense of ref. 4, which is an abrupt change in the state of the system at one or more times separating periods of stasis. The second is an ongoing smooth change in the state of the system over time (which we refer to as regime evolution). We compared the statistical fit of both regime evolution and shift to the data and found the evolving models better describe the observed statistical variation of SIE [See Methods].

We consider evolving versions of the Auto-Regressive Moving Average (ARMA) models because this allows the structural parameters to evolve smoothly over time, better representing the state of the structure at each point in time. Here we differ from the mean shifted regime shift used by ref. 1 which identified two points of change in the time series of observed sea ice extent, separating it into three different periods of stasis. We differ also from4 who used a single regime shift, 2007, identified by ref. 1. Specifically, we created a single time series, merging the reconstructed (1899–1978) and satellite-observed (1979-2024) time series of monthly total sea ice extent anomalies. To this time series, we fit ARMA models within a Bayesian framework15,16 [See Methods].

Figure 3 shows the evolving persistence, ρt, over the time period (posterior mean in black). A large ρt (>0.95) represents strong persistence in the anomalies, meaning that the present state is strongly driven by the past. The red dashed lines are the upper and lower pointwise 95% credibility intervals for ρt at each time t. Figure 3 shows that persistence is always an important contributor to Antarctic sea ice variability. The strength of that persistence is directly related to the magnitude of the correlation of the anomalies from successive months, that is, the size of the ARMA auto-regressive coefficients. If the anomalies are uncorrelated, ρ = 0 and shocks to the anomalies are not persistent at all. For all values of ρt less than 1, the anomaly will return to zero (the climatological mean) over time. That time is longer at larger ρt and when it is 1 or greater, return to the mean is not guaranteed. Figure 3 shows a level of about ρt = 0.95 in the pre-satellite era, with perhaps a modest decline in persistence over the 1960s until the 1990s. This is followed by a strong and steady increase in persistence since about 2000, transitioning to non-mean reverting behavior15 after 2020. We quantify the information in Figure 3 using Bayesian measures of evidence17 [See Methods]. We find strong statistical evidence that the ρt coefficient is not constant over time, that is, evidence of non-stationarity in the auto-correlation structure. Much of the change in the sea ice variability since the beginning of the 20th century has come since the mid 2000s [See Methods]. If there were a regime shift then the persistence curve in Figure 3 would be at a constant level until the change-point, followed by a new constant level until the next change-point. We find strong statistical evidence that this regime evolution model fits better than regime shift models with one or more change points1 [See Methods].

Fig. 3: Estimate of the evolving persistence, ρ, over time.
figure 3

The red dashed lines are the upper and lower pointwise 95% credibility intervals for the persistence at that time. The pattern suggests a steady increase in persistence since about 2000 with very high levels after 2020.

Full size image

Antarctic SIE varies regionally and the total SIE, being the aggregate, may disguise the individual variability exhibited by the different sea ice sectors. Prompted by this knowledge, we investigated the time series of SIE anomalies in the five sectors using the same modeling framework as for the total. Interestingly, and not unexpectedly, the sectors differ from each other. The time-varying persistence plots for the five sectors are given in Supplementary Fig. 9. King Haakon VII and East Antarctica are similar to the total, although more muted, showing increases in persistence since the 1990s and rapid increases since the mid 2000s. The Weddell and Ross-Amundsen Seas sectors exhibit only modest changes in persistence and the Amundsen-Bellingshausen Sea has modest fluctuations. We find strong statistical evidence that the persistence is not constant over time in King Haakon VII and East Antarctica.

The difference in behavior exhibited by sea ice in the different sectors is rooted in their relationships with the atmospheric circulation, the ocean and their geography. While these are not explored here, a recent study noted that the magnitude and processes of the Antarctic sea ice extent drop from 2016 to low values in 2023 also differs regionally, with a more dominant role for the ocean (compared to the winds) across much of the Eastern Hemisphere, similar to our regions where the evolving persistence has changed the most18. Nonetheless, in our reconstruction framework, we can examine statistically the relationship between the total sea ice extent anomalies and the anomalies of the different sectors. There are strong correlations between the total sea ice extent anomalies and the anomalies in the King Haakon and East Antarctica sectors. These are the two sectors that exhibit persistence patterns much like that of the total Antarctic. The correlations with the other three sea ice sectors, with less similar patterns, are weaker. Of further interest is that the degree of correlation between the total and the King Haakon and East Antarctica sectors has increased over the period 2020–2024, and not for the other sea ice sectors. Prior to 2020 the sea ice sectors had correlations ranging between 0.4 and 0.6 with the total. However, since 2020 those values have increased for King Haakon VII (0.56 to 0.86) and East Antarctica (0.46 to 0.65) and their increased persistence contributes to that in the total.

The results from this regime evolution analysis suggest that the extreme maxima and minima in total sea ice extent observed in recent times are evidence of a structural change in the sea ice from a quasi-stationary (pre-2000) to a non-stationary system with increasing persistence (post-2016). Over the period 1979–2016 the temporal variability of Antarctic sea ice extent, controlled by the strong physical relationships with the atmosphere and ocean, displayed strong seasonality, strong interannual variation, subdecadal variation and a weak but significant positive trend19. These are all examples of non-stationary variation where the sea ice extent has always had a strong tendency to return to the mean state. Since 2016, however, the sea ice variability has displayed numerous extreme values chiefly in the summer, and in 2023 and 2024 for summer, winter, and spring. The frequency of these extremes is highly unusual in the reconstructed sea ice data and suggests that the temporal variability of Antarctic total sea ice extent has a much weaker tendency to revert to its climatological mean state since 2016. This further suggests that the long term predictability in the Antarctic sea ice system is reduced, that this reduction began in the early 2000s, and is being replaced by shorter term predictability associated with strong persistence.

Discussion

The 20th century reconstructions of sea ice extent provides valuable context within which to view the contemporary variability in Antarctic sea ice. From the probability analysis, it seems highly unlikely that anomalies (in both size and frequency) like the observed record negative anomalies in Antarctic SIE have occurred during the earlier 20th century. This is in agreement with ref. 7 who based their conclusions on a seasonal reconstruction. This suggests that these extremes are beyond those expected from the natural variability estimated from 2500 reconstructions, each spanning over 70 years, and supports the growing opinion that the recent anomalous behavior of Antarctic sea ice is indicative of a structural change in the Antarctic atmosphere-ocean-sea ice system1,4.

The evolving structural analysis of the merged reconstructed data and the satellite-observed sea ice extent shows that there has been indeed a change in the system, which is associated with continuous increasing persistence in the sea ice extent anomalies. This persistence moved the sea ice variability from a quasi-stationary state - a tendency to return to the mean/median -, to a non-mean reverting, that is, a state characterized by very strong persistence of extremes. This finding of increasing persistence is similar to that of ref. 4 who also used increased persistence as their measure of structural change in the summer total Antarctic sea ice regime. However, it is different from the findings of ref. 1 who suggested an abrupt shift in the mean state of the sea ice based on change point analysis. Note that ref. 4 used the 2007 change point identified by ref. 1 as the temporal boundary in their study. Despite these comparisons, there are two key differences between the study reported on here and these two. One is the use of the reconstructed sea ice data to contextualize the contemporary variation in sea ice in a much longer timescale; theirs used data from the satellite-observed period only. The other is the use of a regime evolving model to assess the changing structure of Antarctic sea ice under the assumption that change would occur as a smooth evolution rather than an abrupt shift. This allows us to show that while there was a reduction in total sea ice extent over the 20th century, that change was not structural. By contrast, the 21st century extreme anomalies in total Antarctic sea ice are a manifestation of structural change, that is, increased persistence, beginning in the early 2000s.

While much of the discussion of structural change focuses on the total Antarctic SIE, the regional contributions to the total variation have, until now, not been assessed. Our evolving structural analysis of the five sea ice sectors identified by ref. 9 underscores the complexity of sea ice variability around Antarctica. Two sectors exhibit strong evidence of structural change due to increased persistence, two show modest evidence and the fifth shows modest fluctuations in persistence but no sustained change. Clearly, further investigation into the regional variability is necessary.

While ref. 1 and ref. 4 may have used different approaches, there is at least a first order agreement with the current study that the Antarctic sea ice system has undergone a structural change. Such a fundamental change, especially one identified by increasing persistence, is most likely not related to atmospheric variability since that tends to lead to shorter term variation e.g., seasonal to interannual20; rather, it may be related to sustained subsurface ocean warming which began in the 20th century, prior to the recent record negative extremes in sea ice extent, and is attributed to greenhouse warming1. While the cause of the change in variability of Antarctic sea ice extent is still being established, our evolving structural analysis suggests that we might no longer be able to rely on the past, long term, behavior of the sea ice system to predict its future state. Extreme conditions may continue to characterize the future state of Antarctic sea ice.

Methods

Data and data availability

The monthly sea ice extent reconstructions are those of ref. 8. They are primarily based on monthly mean pressure and temperature records across the Southern Hemisphere extratropics and midlatitudes from 1905 to 2020. These records were used in previous research7,21 and obtained from the University Corporation for Atmospheric Research data archive dataset ds570.0 (https://rda.ucar.edu/datasets/ds570-0/)22. A few stations were patched with nearby stations using a monthly mean offset7.

We computed sea ice extent using satellite-observed sea ice data from the Nimbus-7 Scanning Multichannel Microwave Radiometer and the Defense Meteorological Satellite Program Special Sensor Microwave Imager—Special Sensor Microwave Imager/Sounder (SSM/I-SSMIS). We used the CDR daily concentration fields from the NOAA/NSIDC CDR of Passive Microwave Sea Ice Concentration, Version 4 (https://nsidc.org/data/g02202)23.

The data span the period 25 October 1978 to 31 October 2024 and are daily except before July 1987, when they are given every other day. We extended this data with the Near-real-time NOAA/NSIDC Climate Data Record of Passive Microwave Sea Ice Concentration (NRT CDR) data set, which is the near-real-time version of the data set G02202 until 31 October 202424. The data are gridded on the SSM/I-SSMIS polar stereographic grid (25 km × 25 km). The sea ice extent used in our analysis is calculated using the equatorward limit of the 15% sea ice concentration isoline. It is thus the sum of the area of every grid cell that is 15% or more covered with sea ice. In addition to the alternate-day observations from 1978 to 1987, there are a number of days and segments of days with no observations. In particular, there are no data between 3 December 1987 and 12 January 1988. For these days, we fit a stochastically imputed daily sea ice extent using a prior procedure7. The monthly sea ice extent values were computed by averaging all days in the month (recorded and imputed). We note that, except for the period from 3 December 1987 to 12 January 1988, the impact of this stochastic multiple imputation scheme is small, since the daily data are nearly complete. The sectoral sea ice extent was computed as the sum of the area within the sector of every grid cell that is above 15% or more covered with sea ice (allocating the areas of cells that intersect two sectors proportionally). The longitude bounds for the sectors are as follows: Amundsen-Bellingshausen Seas (250∘E–290∘E), Weddell Sea (290∘E–346∘E), King Haakon VII (346∘E-71∘E), East Antarctica (71∘E-162∘E) and Ross- Amundsen Seas (162∘E–250∘E). The total Antarctic sea ice extent represents the area of all sea ice surrounding Antarctica and is precisely equal to the sum of the areas in the five sectors.

Reconstruction methodology

A statistical model was used to create ensemble reconstructions of monthly Antarctic Sea ice extent from 1899 to 1979. A detailed technical description of the model is available8,25. Here we provide an overview. The core statistical model is a Vector Auto-Regressive Moving Average (VARMA) model for the monthly sectoral sea ice extents. It is fit to the satellite observed Antarctic Sea ice extent from August 1978 to December 2020 aggregated to the monthly level. The fit and assessment of the validity of the model and fit is within the Bayesian framework. The model has a regression mean structure to incorporate information from the station data. The structural parameters are allowed to vary by season. This model framework incorporates the auto-correlation structure of sea ice over time as well as the dependence of sea ice between the sectors.

The Bayesian framework has a number of advantages in this setting. It naturally incorporates model uncertainty, parameter uncertainty, and unexplained variability in its unknowns, in our case the reconstructed sea ice extent. A last but maybe most important argument for the Bayesian framework is that it naturally allows us to incorporate prior knowledge of model parameters in the form of prior distributions. In this situation, we know that the sea ice only has a weak relationship with measurements from each individual station in the Southern hemisphere and that the sea ice in many sectors is likely (conditionally) unrelated to most measured weather. That is, while the station data as a whole is informative about the sea ice extent, this information may be carried by a small subset of stations. This subset may vary by sector or season. Specifically, our model incorporates a sparsity prior on the regression coefficients26. This represents the prior belief that the measurements of most weather stations to have no partial association with the sea ice extent in a specific sector, but some stations might have reasonably strong predictive power27.

Perhaps most importantly, it automatically provides a generative mechanism for ensembles of reconstructions, that is, many plausible reconstructions for all sectors over the entire time period. Each individual ensemble member is a reconstruction and has a plausible month-to-month progression and overall trend for the sea ice in each sector, incorporating credible relationships between the reconstructions in each sector. These ensembles incorporate all sources of uncertainty and can readily be used in further analyses, as in this paper.

Event probability methodology

Consider an event that can be expressed in terms of monthly sea ice extent values from 1900 to 2023. That is, it is an event for which one can determine if it occurred or not based on knowledge of the monthly sea ice extent values from 1900 to 2023. An example of such an event is: Was there a decline in total Antarctic SIE of a least 4.18 million km2 in a three-year window from 1900 to 2023?

As the sea ice extents for months prior to the satellite-observed period are at least partially unknown we cannot determine if such events occurred or did not. However, we can use the ensemble reconstructions to compute the probability that the events occurred as the posterior probability over the ensemble. Specifically, the ensembles represent the posterior distribution of the sea ice extent values, so that the probability of the event is the proportion of times the event over the posterior distribution. This probability can be computed by taking the proportion of times the event occurs over the ensemble. Specifically, the stated probabilities are the proportion of times the event occurs over the 2500 ensemble members.

Structural change methodology: Regime shift models

We start as our baseline model the model that was used to create the reconstructions8,25. This VARMA (Vector Auto Regressive Moving Average) model is stationary over time in the sense that the model parameters do not change over time. We modify and generalize the model in different ways for either the regime shift or evolution models.

We consider two forms of structural change: regime shift and regime evolution. In this sub-section we consider regime shift and in the next we consider regime evolution.

To allow for changing parameters, we posit the existence of a latent partition of time into disjoint periods with each period having different parameters. To represent this, we modified Auto-Regressive Integrated Moving Average (ARIMA) models15 to have one of more latent regime shift points. The time(s) of regime shift are an unknown parameter of the model. The model allowed different mean, variance, autoregressive and moving average parameters before and after each regime shift point. This model is significantly more sophisticated than that used in ref. 1, who only test for mean shifts and assume the anomalies are independent from month-to-month. We fit the parameters within a Bayesian framework16 on the merged satellite-observed time series (1979–2023) and reconstruction time series (1899–1978) of monthly total sea ice extent anomalies. The integrated component is an extension of ARMA allowing for non-mean reverting type behavior (if supported by the data; we did not find support for integration within this model class). We considered a wide range of such models with auto-correlation up to 12 months and order two moving averages. To choose good fitting models we use the out-of-sample pointwise predictive accuracy using the expected log pointwise predictive density for a new dataset (ELPD). This was estimated using leave-one-out (LOO) cross-validation17. The best fitting model using a range of AR, MA and integrations is the model with one-month, four month and 12 month autoregressive, and lag one and 12 moving average (MA) components. The estimated ELPD values for some candidate models are given in Table 1. The static/stationary models are special cases of the regime shift models (that is, with constant parameters over time) so their fit to the data can be directly compared to the regime shift models. As can be seen from Table 1, the three regime model is the best regime shift type model. It has an ELPD of -1278.3, a modest 3.3 units better than the one shift model. The most probable single change point is July 2007. There is some evidence for a second change point, and this would be in August 1988. We note that there was an instrument change at about this time and the movement from every-other-day to daily measurements. Finally, both of these models are better than the no regime shift model (ELPD  = −1283.6).

Table 1 Comparison of the out-of-sample pointwise predictive accuracy of various models using the expected log pointwise predictive density for a new dataset (ELPD-LOO)
Full size table

Structural change methodology: Regime evolution models

While regime shifts have their appeal, most mechanisms of structural change are unlikely to be discrete in this way, but are much more likely to be continuously changing (perhaps with long periods of stasis). Hence, we allow the parameters to be slowly varying deterministically as functions of time. Specifically, the ARMA parameters were modeled as spline functions using a natural spline basis, with coefficients estimated within the Bayesian framework. We considered a wide range of such models, allowing the auto-regressive parameters for monthly lags of 4, 12 and moving-average 1 and 12 to be smooth functions of time. To choose good fitting models we again used the out-of-sample pointwise predictive accuracy using the expected log pointwise predictive density for a new dataset (ELPD). The best fitting model using a range of ARMA models is the one with one evolving lag one-month autoregressive component and fixed lag 4 and 12 components as well as static 1 and 15 month moving average (MA) components. The estimated ELPD value for the model is given in Table 1. The static/stationary model with no regime shift is a special cases of the evolving models (that is, with constant parameters over time) so their fit to the data can be directly compared to the regime evolving models. As can be seen from Table 1, the evolving models fit substantially better than the regime shift models, including the best three regime models.

Measuring Persistence

The concept of persistence is an important one for understanding SIE variation over time. By persistence is meant the long-run effect of a shock to the sea ice system. By shock we mean an unexpected event, such as a weather event that changes the sea ice anomaly at a point in time. For example consider a storm that affects the sea ice distribution increasing the extent by 1%. By how much do we expect it to be higher at some future point in time and how long will it take to return to its pre-storm level? If the anomaly is persistent it will last a long time, otherwise its effect will dissipate.

How best to measure persistence? Consider the ARMA(p, q) model with p autoregressive terms and q moving-average terms of the form

$${Y}_{t}=c+{\sum }_{i=1}^{p}{A}_{i}{Y}_{t-i}+{\sum }_{j=1}^{q}{B}_{j}{\varepsilon }_{t-j}+{\varepsilon }_{t},$$

with Ai denoting the ith autoregressive coefficient, Bj denoting the jth moving average coefficient and εt being the error terms. This model can be rewritten as

$${{{\bf{Y}}}}_{t+1}={{\bf{C}}}{{{\bf{Y}}}}_{t}$$

where Yt = (Yt, …, Yt−p+1) and C is an appropriate coefficient matrix formed from the prior equation. Consider sequentially updating k = 1, 2, … so that

$${{{\bf{Y}}}}_{t+k}={{{\bf{C}}}}^{k}{{{\bf{Y}}}}_{t}$$

Hence the dependence of Yt+k on Yt, k = 1, 2, … is determined by powers of C, themselves determined by the largest eigenvalue of C (in modulus), ρ. We then take this ρ to be the measure of persistence. A value of ρ = 0 means no dependence and ρ = 1 means permanent impact. It is also possible for ρ > 1, indicating that the impact of a shock grows over time rather than dissipating. This choice has been extensively used in financial time series, such as for measuring the persistence of inflation in the presence of supply chain shocks5.

Sensitivity of the persistence measure

The evidence for regime evolution is expressed by the structural model for the sea ice extent process as well as the Bayesian framework used to estimate that model. While the credibility intervals in Fig. 3 reflect the certainty with which we know the persistence over time, there is always the danger of computational or model artifacts impacting the results. We address this in two ways. First, we augmented the satellite observations with the reconstructions going back to 1899. The pre-satellite reconstruction period should be stable, and is.

The second way is to implement a sensitivity analysis by constructing a (counter-factual) sea ice record by swapping the last seven years of data with a segment of the same size centered on 1960. We then recomputed the persistence function in Fig. 3. If the rapid change in persistence post-2015 was an artifact of the model or method then this counterfactual data record would show a similar anomaly as the actual data. It does not. It does, however, show a spike in persistence around 1960 and no spike elsewhere (e.g., nothing from 2010 onward). We repeated this process with other years than 1960 with similar results. Taken together, these results provide evidence that the sharp increase in Fig. 3 is not an artifact of the model or method.