Introduction

Evolution has resulted in the speciation and adaptation of various organisms. Although natural selection applies to all kinds of species, the resulting natural population structures have dramatic differences. Especially due to their lack of mobility, plants, compared to humans and most animals, have established much stronger population structures adapted to specific local environments (Crawley 2009). This makes it difficult, for instance, in modern genomic studies, to distinguish genotypic effects on plants’ phenotypes from geographical stratification (Atwell et al. 2010).

Fast-developing genotyping techniques have made genome-wide association study (GWAS) one of the most useful approaches for discovering genomic loci that regulate phenotypes in various organisms (Atwell et al. 2010; Hirschhorn and Daly 2005; Huang et al. 2010; Liu et al. 2023; Uffelmann et al. 2021). In human GWAS, we learned that most of the loci discovered to be associated with complex traits or diseases have very small effects (Yang et al. 2010; Zeng et al. 2021). The single nucleotide polymorphisms (SNPs) discovered need to have sufficiently high minor allele frequencies (MAFs) for the statistical tests to gain enough power, while high-MAF variants tend to have small effects on the studied phenotypes as these variants are under weak selection pressure. Alleles that have high penetrance on a phenotype are normally under strong selection, resulting in low MAFs of the corresponding SNPs. Thus, a major challenge in human GWAS appears to be the trade-off between statistical power and effect size of the detected variant (Korte and Farlow 2013; Visscher et al. 2017; Wellenreuther and Hansson 2016; Yang et al. 2014).

Although a similar trade-off also applies to GWAS in plant populations, e.g. in the natural population of Arabidopsis thaliana, in terms of discovery power, the major challenge is different. As each individual plant accession is sampled from a specific geographical ___location in the world, accessions with different genotypes normally have much greater phenotypic differences compared to those in humans. It appears that the genome can explain a large proportion of variation in the plant phenotype; however, the population structure in nature is highly complex, which can significantly confound genomic effects due to genetic background (Atwell et al. 2010). The challenge arises from linkage disequilibrium and associations inherent in the population structure. For instance, an allele may exert a positive effect on a trait, but due to the population structure, it could be statistically associated with alleles that negatively impact the trait. This association complicates the measurement and detection power of the allele’s true effect on the phenotype.

As a community-based effort, over 1000 natural A. thaliana accessions have been collected from worldwide geographical locations (Kawakatsu et al. 2016; The 1001 Genomes Consortium 2016). Most of those plants have been sequenced for genome, transcriptome, and even methylome, and these datasets have been made publicly available for researchers worldwide. Many accessions in this collection have been phenotyped for developmental, metabolic, ionomics, and stress resistance traits (Atwell et al. 2010), and more and more phenotypes are gradually being released. Previous analyses in those datasets have revealed substantial connections between genotypic and phenotypic variations in this species. The application of association mapping has provided insights into the genetic basis of complex traits (Atwell et al. 2010; Casellas et al. 2023; Shen et al. 2012, Wang et al. 2017, Zan and Carlborg 2019), adaptation (Ferrero-Serrano and Assmann 2019; Kang et al. 2023; Shen et al. 2014), and the evolutionary process (Chan et al. 2010; Liang et al. 2020). Nevertheless, many essential genotype-phenotype links are still difficult to establish based on the current GWAS data, due to the substantial population stratification, highly correlated with the sampling origins of the plants. Therefore, novel powerful analyses are required to further uncover the hidden genetic regulation.

Based on publicly available A. thaliana datasets (Atwell et al. 2010; Kawakatsu et al. 2016; Schmitz et al. 2013; The 1001 Genomes Consortium 2016), here, we aim to examine the application of a bivariate analysis method that combines the discovery power of two correlated phenotypes with accounting for population structure (Shen et al. 2017), in order to map novel loci that simultaneously influence both traits. We justify the ability of the summary-statistics-based approach in handling population stratification, even when the population structure is strong. We interpret the statistical significance with the discovered dual-trait genotype-phenotype map. We try to replicate and in silico functionally investigate the candidate genes that may drive such associations.

Methods

Genome-wide 250k SNP array genotype data and phenotype data for 199 natural Arabidopsis thaliana accessions

We downloaded a public dataset on the collection of 199 natural Arabidopsis thaliana inbred lines, containing 107 phenotypes including 23 flowering-time-related phenotypes and 43 developmental phenotypes, along with corresponding genotypes with 214,051 SNPs available (Atwell et al. 2010). After filtering out the variants with minor allele frequencies less than 0.10, 173,220 SNPs remained.

Whole genome re-sequencing and RNA-seq data for a population of 1,135 natural A. thaliana accessions

1135 natural Arabidopsis thaliana accessions have been collected and sequenced for the whole genome and transcriptome (Kawakatsu et al. 2016; The 1001 Genomes Consortium 2016). We downloaded this sequencing dataset and removed the accessions with no measured phenotype and SNPs with minor allele frequency below 0.05 and a call rate below 0.95. The final dataset includes 1001 individuals with 1,797,898 SNPs and measured flowering time at both 10 °C and 16 °C. To scan for candidate genes, we also downloaded the transcriptome dataset of a subset of this collection (n = 728) (Kawakatsu et al. 2016). The final eQTL scan dataset contains RNA-seq derived RPKM-values for 24,150 genes in 648 accessions whose phenotypic and genotypic data are both available.

Whole genome re-sequencing derived SNP genotype and RNA-sequencing derived transcriptome data for a population of 144 natural A. thaliana accessions

In a prior study, Schmitz et al. conducted RNA sequencing on a set of 144 natural A. thaliana accessions (Schmitz et al. 2013). We downloaded this data together with their corresponding whole-genome SNP genotypes available as a part of the 1001 Genomes project (Kawakatsu et al. 2016; The 1001 Genomes Consortium 2016) to replicate our SMR findings. Following the quality control procedure in the previous study (Zan et al. 2016), we removed two accessions (Alst_1 and Ws_2) from the data due to missing genotype data and two accessions (Ann_1 and Got_7) due to their low transcript call rate (16,861 and 18,693 genes with transcripts as compared to the range of 22,574 to 26,967 for the other accessions). The final dataset used for eQTL mapping included 1,347,036 SNPs with MAF above 0.05 and call rate above 0.95 for 140 accessions, and corresponding RNA-seq derived FPKM-values for 33,554 genes.

Single-trait genome-wide association analysis accounting for highly stratified population structure

For all available traits in this dataset, we first performed a mixed model-based single-trait genome-wide association analysis to generate single-trait summary statistics. These summary statistics were used as input for the dual-trait analysis described in the following section. To replicate our signal, we also performed a single-trait genome-wide association analysis using a collection generated in a 1001 Genomes project (The 1001 Genomes Consortium 2016). To correct for the population structure in these A. thaliana accessions, a single-trait genome-wide scan was performed based on linear mixed models, using the polygenic and mmscore procedure in GenABEL (Aulchenko et al. 2007).

Estimation of the phenotypic correlation for bivariate association analysis

In the absence of population structure, the phenotypic correlation coefficient between the two traits can be unbiasedly estimated by the correlation of genome-wide Z-scores from single-trait GWAS. Linear mixed models were utilized to correct for population stratification in each single-trait GWAS; thus, intuitively, the use of the summary association statistics from single-trait analyses does not carry the issue of population stratification. However, it is unclear whether population structure affects this particular approach for estimating phenotypic correlation. Below, we introduce the theoretical basis for this estimation procedure (see also Ning et al. 2021).

In order to model the behavior of the correlation of genome-wide association test statistics, we describe a random effect model for the phenotypic value. For n individuals, let the genotype vector g be centered, we have the phenotype vector for each trait as yi = gβi + Gi + ei (i = 1, 2), where βi is the genetic effect at a certain variant, satisfying

$$\left(\begin{array}{c}{\beta }_{1}\\ {\beta }_{2}\end{array}\right) \sim N\left({{{\bf{0}}}},\left[\begin{array}{cc}{\sigma }_{{\beta }_{1}}^{2}&{r}_{g}{\sigma }_{{\beta }_{1}}{\sigma }_{{\beta }_{2}}\\ {r}_{g}{\sigma }_{{\beta }_{1}}{\sigma }_{{\beta }_{2}}&{\sigma }_{{\beta }_{2}}^{2}\end{array}\right]\right),$$

and for the rest of the genome,

$$\left(\begin{array}{c}{{{{\bf{G}}}}}_{1}\\ {{{{\bf{G}}}}}_{2}\end{array}\right) \sim N\left({{{\bf{0}}}},\left[\begin{array}{cc}{\sigma }_{1}^{2}{{{{\bf{I}}}}}_{n\times n}&{r}_{G}{\sigma }_{1}{\sigma }_{2}{{{{\bf{1}}}}}_{n\times n}\\ {r}_{G}{\sigma }_{1}{\sigma }_{2}{{{{\bf{1}}}}}_{n\times n}&{\sigma }_{2}^{2}{{{{\bf{I}}}}}_{n\times n}\end{array}\right]\right).$$

rg and rG are the genetic correlations between the two traits at this particular variant and the rest of the genome, respectively. For the Arabidopsis inbred lines, the phenotypes were obtained by taking the mean phenotypic value of repeated measurements for each accession (Atwell et al. 2010). This yields nearly completely genetic phenotypes, so that ei approximates zero.

In single-trait GWAS, we have \({\hat{\beta }}_{i}={{{{\bf{g}}}}}^{{\prime} }{{{{\bf{y}}}}}_{i}/{{{{\bf{g}}}}}^{{\prime} }{{{\bf{g}}}}\), then

$$\begin{array}{lll}{{{\rm{var}}}}({\hat{\beta }}_{i})\;=\;\frac{{{{\rm{var}}}}({{{{\bf{g}}}}}^{{\prime} }{{{{\bf{y}}}}}_{i})}{{({{{{\bf{g}}}}}^{{\prime} }{{{\bf{g}}}})}^{2}}\\\qquad\quad\;\;\,=\;\frac{{{{\rm{var}}}}({{{{\bf{g}}}}}^{{\prime} }{{{\bf{g}}}}{\beta }_{i}+{{{{\bf{g}}}}}^{{\prime} }{{{{\bf{G}}}}}_{i})}{{({{{{\bf{g}}}}}^{{\prime} }{{{\bf{g}}}})}^{2}}\\\qquad\quad\;\;\,=\;{\sigma }_{{\beta }_{i}}^{2}+{\sigma }_{i}^{2}{({{{{\bf{g}}}}}^{{\prime} }{{{\bf{g}}}})}^{-1}\end{array}.$$

So that

$$\begin{array}{lll}{{{\rm{cor}}}}({z}_{1},{z}_{2})\,=\,\frac{{{{\rm{cov}}}}({{{{\bf{g}}}}}^{{\prime} }{{{{\bf{y}}}}}_{1},{{{{\bf{g}}}}}^{{\prime} }{{{{\bf{y}}}}}_{2})}{\sqrt{{({{{{\bf{g}}}}}^{{\prime} }{{{\bf{g}}}})}^{2}{\sigma }_{{\beta }_{1}}^{2}+\,{{{{\bf{g}}}}}^{{\prime} }{{{\bf{g}}}}{\sigma }_{1}^{2}}\sqrt{{({{{{\bf{g}}}}}^{{\prime} }{{{\bf{g}}}})}^{2}{\sigma }_{{\beta }_{2}}^{2}+\,{{{{\bf{g}}}}}^{{\prime} }{{{\bf{g}}}}{\sigma }_{2}^{2}}}\\\qquad\qquad\;\;\approx\, \frac{({{{{\bf{g}}}}}^{{\prime} }{{{\bf{g}}}})({{{{\bf{g}}}}}^{{\prime} }{{{\bf{g}}}}){{{\rm{cov}}}}({\beta }_{1},{\beta }_{2})+\,{{{{\bf{g}}}}}^{{\prime} }{{{\rm{cov}}}}({{{{\bf{G}}}}}_{1},{{{{\bf{G}}}}}_{2}){{{\bf{g}}}}}{\sqrt{{({{{{\bf{g}}}}}^{{\prime} }{{{\bf{g}}}})}^{2}{\sigma }_{{\beta }_{1}}^{2}+\,{{{{\bf{g}}}}}^{{\prime} }{{{\bf{g}}}}{\sigma }_{1}^{2}}\sqrt{{({{{{\bf{g}}}}}^{{\prime} }{{{\bf{g}}}})}^{2}{\sigma }_{{\beta }_{2}}^{2}+\,{{{{\bf{g}}}}}^{{\prime} }{{{\bf{g}}}}{\sigma }_{2}^{2}}}\\\qquad\qquad\;\;=\,\frac{({{{{\bf{g}}}}}^{{\prime} }{{{\bf{g}}}})({{{{\bf{g}}}}}^{{\prime} }{{{\bf{g}}}}){r}_{g}{\sigma }_{{\beta }_{1}}{\sigma }_{{\beta }_{2}}+\,{{{{\bf{g}}}}}^{{\prime} }{{{\bf{g}}}}{r}_{G}{\sigma }_{1}{\sigma }_{2}}{\sqrt{{({{{{\bf{g}}}}}^{{\prime} }{{{\bf{g}}}})}^{2}{\sigma }_{{\beta }_{1}}^{2}+\,{{{{\bf{g}}}}}^{{\prime} }{{{\bf{g}}}}{\sigma }_{1}^{2}}\sqrt{{({{{{\bf{g}}}}}^{{\prime} }{{{\bf{g}}}})}^{2}{\sigma }_{{\beta }_{2}}^{2}+\,{{{{\bf{g}}}}}^{{\prime} }{{{\bf{g}}}}{\sigma }_{2}^{2}}}\\\qquad\qquad\;\;=\,\frac{nf(1-f){r}_{g}{\sigma }_{{\beta }_{1}}{\sigma }_{{\beta }_{2}}+\,{r}_{G}{\sigma }_{1}{\sigma }_{2}}{\sqrt{nf(1-f){\sigma }_{{\beta }_{1}}^{2}+\,{\sigma }_{1}^{2}}\sqrt{nf(1-f){\sigma }_{{\beta }_{2}}^{2}+\,{\sigma }_{2}^{2}}}\end{array}$$

where f is the minor allele/genotype frequency for the inbred lines. This correlation between Z-scores serves as an estimate of phenotypic correlation because the term \(nf(1-f){\sigma }_{{\beta }_{i}}^{2}\ll {\sigma }_{i}^{2}\), as \(E[{\sigma }_{{\beta }_{i}}^{2}]\approx {\sigma }_{i}^{2}/M\) and n ≪ M, where M is the number of variants in the study. Therefore, as long as n is not huge, cor(z1, z2) reduces to rG, which is approximately the phenotypic correlation for the inbred lines population. The dual-trait analysis exclusively relies on summary association statistics. In the context of using the statistics for phenotypic correlation estimation, the only assumption is that the heritability explained by each individual variant is small. This approach does not require individual-level data and thus not affected by individual-level data measurement accuracy.

As the single-trait GWA analysis is performed using the linear mixed model to correct for population structure, the vector of test statistics z is not inflated. With the theory above, population stratification might still inflate the multivariate test statistic through genetic correlation, as the LD structure is complicatedly distributed across the genome. Nevertheless, the impact of population structure on the estimation of R needs to be examined empirically for each structured population.

Dual-trait genome-wide association analysis in inbred lines using summary association statistics

We performed dual-trait genome scans using our recently developed multivariate analysis method implemented in the MultiABEL package (Ning et al. 2021; Shen et al. 2017). The method takes the whole-genome summary statistics to infer phenotypic correlation coefficients and conducts MANOVA analysis. The core test statistic of the bivariate test is Hotelling’s T2, which follows a χ2 distribution with two degrees of freedom for the two phenotypes, i.e.

$${T}^{2}={{{{\bf{z}}}}}^{{\prime} }{{{{\bf{R}}}}}^{-1}{{{\bf{z}}}},$$

where R is a 2 × 2 matrix with the off-diagonal elements being the correlation coefficient between the two Z-scores in single-trait GWAS, for the two traits at the same variant. As shown above, this correlation coefficient is proportional to the phenotypic correlation (on the liability scale for binary traits) (see also Zhu et al. 2015).

Simulations

In order to examine the performance of the bivariate association test in the highly stratified Arabidopsis population, we conducted a series of simulations. Summary-level data were derived from single-trait GWAS analyses using simulated individual-level data. First of all, we simulated two phenotypes y1 and y2 as

$${{{{\bf{y}}}}}_{i}={{{{\bf{x}}}}}_{i}{\beta }_{i}+{{{{\bf{Z}}}}}_{i}{{{{\bf{b}}}}}_{i}+{{{{\bf{e}}}}}_{i}\,(i=1,2)$$

where xi and Zi are the genotypes for the causal SNP and the SNPs that determine population structure underlying phenotype yi, respectively, and βi and bi are the corresponding genetic effects. The population structure was simulated by the polygenic scores Zibi based on 10% randomly selected SNPs from the genome, excluding the SNPs within 500 kb distance to the causal SNP. The polygenic effects bi associated with the underlying population structure of the phenotype were drawn as bi ~ N(0, (h2/M)I), where h2 is the simulated narrow-sense heritability of phenotype yi and M the number of SNPs that carry the polygenic effects. The causal SNP effect \({\beta }_{i}\propto \sqrt{k{h}^{2}}\), where k = 0, 0.001, 0.005, 0.01, 0.05. The genetic effects for the other SNPs were set to zero. The residual ei ~ N(0, (1 − h2)I).

Four scenarios for the genotype data and population structure were simulated, i.e., 1) 199 natural A. thaliana inbred lines genotype data (173,220 SNPs) by Atwell et al.; 2) 199 natural A. thaliana inbred lines genotype data with half of the population structure (173,220 SNPs), where half of the individuals had their genotype data randomly permuted; 3) genotype data of the 1001 Genomes project for A. thaliana (1,797,898 SNPs); 4) genotype data of the 1001 Genomes project for A. thaliana with half of the population structure (1,797,898 SNPs), where half of the individuals had their genotype data randomly permuted.

The heritability value (h2) for each phenotype was set to 0.25 and 0.5 in each scenario. The phenotypic correlation (rP) was set to −0.25, 0, and 0.25. The simulation was repeated 1000 times for each setup.

Method comparisons

We used the above-simulated data to assess the performance of MultiABEL, our summary-statistics-based approach, in comparison to GEMMA when applying bivariate association tests in the highly stratified Arabidopsis population. GEMMA offers a solution by fitting multivariate linear mixed models (mvLMMs) for testing associations between genotypes and multiple correlated phenotypes using individual-level data (Zhou and Stephens 2012, 2014).

We also evaluated the computational efficiency of these two approaches. We re-sampled 1/5, 2/5, 3/5, 4/5, and all of the total SNPs from the genotype data of 199 natural A. thaliana inbred lines and the 1001 Genomes project, respectively. Each resampling was conducted with 10 replicates, and the analyses were carried out on a single core of the Intel Xeon Platinum 8176 CPU 2.10 GHz processor. For each replicate, we applied both the MultiABEL and GEMMA for the dual-trait analysis.

Genotype-by-environment interaction analysis

We utilized the IIIVmrMLM software (Li et al. 2022a) with the 3VmrMLM method (Li et al. 2022b) to detect QTN-by-environment interactions (QEIs) for two types of flowering time-related traits, respectively. These traits were measured using different methods. One group encompassed six traits in each environment (0W, 2W, 4W, 8W, 0W GH FT, 8W GH FT), while the other group consisted of four traits in each environment (LD, LDV, SD, SDV). The principal components representing population structure were calculated by GenABEL (Aulchenko et al. 2007).

eQTL and SMR analysis

We screened for candidate genes by analyzing the expression data in a subset of the 1001 Genomes collection containing 140 accessions. Expression values for 19 genes around 20 kb up/downstream of the top associated SNP were extracted from (Schmitz et al. 2013). Fourteen genes that did not pass the Kolmogorov-Smirnov test (KS test statistics < 0.8) were filtered out due to potentially unreliable measurements mentioned in (Zan et al. 2016). The remaining five genes were subsequently passed onto eQTL mapping using the qtscore procedure in GenABEL (Aulchenko et al. 2007). Outputs were reformatted according to the description in (Zhu et al. 2016). Together with the flowering time single-trait scan results (The 1001 Genomes Consortium 2016), these were further passed onto SMR analysis scanning for the association between individual gene expression and flowering time. The SMR analysis was repeated for the 5 top candidates, in an independent gene expression dataset containing 648 accessions (Kawakatsu et al. 2016) following the same procedure.

Results

Bivariate genomic scan identifies a hidden locus simultaneously associated with flowering and maturation periods

We re-analyzed a public dataset of a natural A. thaliana collection, where 43 developmental phenotypes and 23 flowering-time-related phenotypes were previously published (Atwell et al. 2010). The number of accessions with measured phenotypes varies from 83 to 193, with a median of 163 (Supplementary Table S1). We first excluded all variants with minor allele frequencies (MAF) less than 0.1 and performed single-trait GWA analysis for all these traits based on a linear mixed model, so that the confounded genetic effects due to population stratification are adjusted. Several SNPs reaching genome-wide significance thus can be detected in the standard univariate analysis. Subsequently, we applied our recently developed multi-trait GWAS method (Shen et al. 2017) to all pairwise combinations of the phenotypes (see Methods). One novel locus, in one of the pairwise tests, reached the most stringent 5% Bonferroni-corrected genome-wide significance threshold for the 2145 pairs of traits and 173,220 variants, i.e. p < 1.35 × 10−10 (Table 1, Fig. 1a). This signal also reaches genome-wide significance in the other six pairs of traits highly correlated with the top pair (Supplementary Fig. S1), without Bonferroni correction for the number of tested trait pairs (Table 1, Supplementary Figs. S2–S7).

Table 1 Discovery and replication analyses results for the novel pleiotropic locus.
Full size table
Fig. 1: Bivariate genome-wide association analysis of two developmental traits.
figure 1

2W: Days to flowering time (FT) under long day (LD) with vernalized for 2 weeks at 5 °C, 8 h daylight, MT GH: Maturation period. a Manhattan plots comparison of bivariate and univariate analysis results, where the novel variants only discoverable when combining two phenotypes are shown in green. The horizontal dashed line represents a 5% Bonferroni-corrected genome-wide significant threshold for the number of variants and also the number of tested trait pairs, respectively. b Zooming in on the novel locus detected using bivariate analysis. r: linkage disequilibrium measured as the correlation coefficient between the top variant and each variant in the region.

Full size image

For the most significant trait combination, 2W (days to flowering time under a long day with vernalized for 2 weeks) and MT GH (maturation period), the linkage disequilibrium (LD) block of this locus (LD r > 0.7) covers about a 260 kb interval on chromosome 1, with a top variant at 3,906,923 bp (dual-trait p = 9.9 × 10−12, Fig. 1b, Table 1). The detected locus shows joint effects on flowering and maturation, where the effect on flowering time (2W) is notably large (15.3 days), and that on maturation period (MT GH) is 2.5 days (Table 1). These correspond to narrow-sense heritability values of 24% and 10% of the two phenotypes, respectively.

Dual-trait analysis is sufficiently powerful to overcome the confounding population structure

The detected joint-effect locus was missed in the corresponding single-trait GWA analysis of 2W (effect = 15.3, p = 2.26 × 10−5 after correcting for population stratification) and that of MT GH (effect = 2.5, p = 3.70 × 10−5). Notably, this locus was not even detectable at the genome-wide significance level in a much larger population of more than 1000 A. thaliana accessions (Kawakatsu et al. 2016; The 1001 Genomes Consortium 2016) due to its severe confounding with the natural population structure. The statistical significance can only be identified when considering the joint distribution of the bivariate statistic. According to the genome-wide Z-scores (student t-statistics), these two phenotypes are negatively correlated, as the plant’s lifespan is relatively stable (estimated and observed phenotypic correlation = −0.55 and −0.68, respectively). However, the observed effects on the two traits are both substantially positive, showing sufficient deviation from the joint distribution that led to bivariate statistical significance (Fig. 2).

Fig. 2: Hexbin scatter plot comparing all Z-scores of the two traits across the genome, showing the bivariate statistical significance of the detected locus.
figure 2

The top variants of the locus are marked on the edge of the empirical bivariate normal distribution with a red circle. The black line with a slope of −1 is provided as a visual guide.

Full size image

The strong confounding with the population structure can also be visualized by the allele frequency distribution of the top associated SNP across different A. thaliana sub-populations based on the genome re-sequencing data from the 1001 Genomes project (The 1001 Genomes Consortium 2016) (Fig. 3). The sub-populations were divided by admixture analysis using ADMIXTURE (Alexander et al. 2009; The 1001 Genomes Consortium 2016). The plus allele increasing flowering time was predominantly found in Sweden and almost fixed in the Northern Sweden population (Fig. 3b; allele frequency = 0.97 in Northern Sweden and 0.51 in Southern Sweden). Overall, the phenotype, e.g. flowering time at 10 °C, highly correlates with the frequency of the plus allele (Fig. 3). The genotype at this locus follows a latitude decline, where the northern accessions are enriched with the plus allele, and the southern accessions are enriched with the minus allele (Fig. 3). This spatially imbalanced enrichment shows strong confounding with the population structure, which is why standard single-trait GWAS loses power substantially.

Fig. 3: The discovered locus is highly confounded with population structure.
figure 3

a Flowering time variation (10 °C) among different sub-populations of Arabidopsis thaliana. These populations are divided by admixture analysis (The 1001 Genomes Consortium 2016); b Frequency of the top associated SNP at chromosome 1, 3,906,923 bp in different sub-populations. The association between the structure of the phenotype and that of the allele frequency shows the population confounding at this locus.

Full size image

Summary-level dual-trait analysis controls confounding-induced statistical bias

The analysis procedure above is intuitively straightforward, without sophisticated bivariate linear mixed modeling. Although the linear mixed model was incorporated in the genome-wide association scan for every single phenotype, it is unclear whether the dual-trait analysis using single-trait summary association statistics can control the confounding due to the substantial structure in the A. thaliana natural population, especially given that long-range LD is common in such populations (Long et al. 2013).

In order to justify our summary-statistics-based approach, we performed a series of simulations (see Methods). The simulation scenarios cover different levels of population stratification, levels of heritability for two phenotypes, various levels of the effect of the causal SNP on each phenotype, and the situations where the directions of causal effects on the two phenotypes are consistent or inconsistent with the phenotypic correlations (Supplementary Figs. S8–11). First of all, we found that the summary-statistics-based dual-trait test was able to control the false positive rates, given that the summary statistics were from the single-trait linear mixed model (Fig. 4, column 1; Supplementary Fig. S16). As expected, if the causal SNP only has an effect on one of the two phenotypes, the dual-trait test would have a slightly lower power than the single-trait analysis (Fig. 4, column 4). Nevertheless, when the SNP has pleiotropic effects on both phenotypes, the dual-trait analysis has better power in detecting the genetic association, especially when the genetic and phenotypic correlations at the causal SNP have opposite directions (Fig. 4, column 5).

Fig. 4: Comparisons of single-trait and dual-trait GWAS results of the target SNP under different simulated scenarios using 199 natural Arabidopsis thaliana inbred lines genotype data.
figure 4

For each scenario, ROC curves represent the true positive rate against the false positive rate with single- and dual-trait GWAS methods from 1000 simulations. The target SNP’s effect size (β) of each phenotype was indicated at the top of ROC plots. The heritability (h2) of each phenotype was set to 0.5, with 10% genome-wide SNPs randomly chosen to simulate population structure. The phenotypic correlation (rP) was set to −0.25, 0, and 0.25, respectively. More scenarios can be found in Supplementary Figs. S8–11.

Full size image

Meanwhile, multivariate methods have been developed to increase statistical power (Kim et al. 2016). Notable examples include MTAG (Multi-trait analysis of GWAS) (Turley et al. 2018), and GenomicSEM (Grotzinger et al. 2019), which are commonly employed for multivariate analyses using summary-level data. Nevertheless, both these approaches rely on summary-statistics-based genetic correlation estimates using LD score regression (Bulik-Sullivan et al. 2015) or high-definition likelihood (HDL) (Ning et al. 2020) with an LD reference for the populations with similar ancestry. This limits their applicability in species other than humans. GEMMA offers a solution by fitting multivariate linear mixed models (mvLMMs) for testing associations between genotypes and multiple correlated phenotypes using individual-level data (Zhou and Stephens 2012, 2014). Thus, we employed simulated datasets to evaluate the performance and computational efficiency of MultiABEL, our summary-statistics-based approach, in comparison to GEMMA when applying bivariate association tests in the highly stratified Arabidopsis populations. The results indicate that both approaches effectively control false positive rates and enhance the power of detecting genetic associations, particularly when the genetic and phenotypic correlations at the causal SNP exhibit opposing directions (Fig. 5a). While the two approaches yield similar performance effects (Supplementary Figs. S8–15), MultiABEL’s use of summary statistics proves to be more convenient and quicker than conducting a full GWAS analysis, and it outperforms GEMMA in terms of computational efficiency (Fig. 5b, c). With the growing availability of summary-level data, MultiABEL exhibits substantial potential for a wide range of applications and is particularly well-suited for handling larger multivariate analyses.

Fig. 5: Performance and computational efficiency comparisons between MultiABEL and GEMMA using simulations.
figure 5

ROC performance of single-trait and dual-trait GWAS results for the target SNP based on genotype data from 199 natural Arabidopsis thaliana inbred lines (Atwell et al.’s dataset) using MultiABEL/GenABEL and GEMMA (a). The effect size of the target SNP was set to \(\beta \propto \sqrt{0.05{h}^{2}}\). The heritability (h2) of each phenotype was set to 0.5, with 10% of genome-wide SNPs randomly selected to simulate population structure. The phenotypic correlation (rP) was set to −0.25. Additional simulation results are presented in Supplementary Figs. S8–15. Computational times for dual-trait GWAS analysis using MultiABEL and GEMMA with the Atwell et al.’s dataset (b) and the 1001 Genomes dataset (c). The Atwell et al.’s dataset comprises 199 individuals with 173,220 SNPs, while the 1001 Genomes dataset includes 1001 individuals with 1,797,898 SNPs. Computation was performed on a single core of the Intel Xeon Platinum 8176 CPU 2.10 GHz processor.

Full size image

Replication of the detected genetic effect on flowering time

Although we lack an independent dataset of A. thaliana maturation duration to replicate the bivariate statistical test, datasets containing additional independent A. thaliana flowering time measurements are available. We downloaded a flowering time GWAS dataset measured in 1135 natural accessions from the 1001 Genomes project collection (The 1001 Genomes Consortium 2016) and performed a single-trait association analysis of our discovered top SNP with linear mixed model correction for the population structure. The genetic effect was significantly replicated for flowering time at 10 °C (effect = 2.5 days, p = 0.006) and flowering time at 16 °C (effect = 4.4 days, p = 0.0008). The observed effects on flowering time in the replication sample are markedly smaller than in the discovery population. This pronounced difference suggests that factors beyond the Winner’s Curse, such as distinct genetic backgrounds, may contribute to the observed variation.

We also screened literature for conventional quantitative trait loci (QTL) studies in intercrosses using natural A. thaliana accessions. Our detected signal is underneath a reported QTL peak for flowering time from an intercross between a Swedish and an Italian population (Dittmar et al. 2014) (Supplementary Fig. S17). This, together with the replication above, justifies the detected association. Although the discovered genetic effect on the maturation period is not directly replicated, the effect does exist when the effect on flowering is justified, as the pleiotropic signal must be driven by both phenotypes.

Prediction and replication of candidate genes using summary-level Mendelian randomization

As a community-based effort, all the natural A. thaliana accessions from the 1001 Genomes project were measured for their transcriptome (Kawakatsu et al. 2016; The 1001 Genomes Consortium 2016). Such a public gene expression dataset allows us to predict candidate genes underlying the association signal. We extracted the expression levels of 19 genes within a ± 20 kb window around the top associated SNP using RNA-seq gene expression measurements from 140 accessions (Schmitz et al. 2013). Among these, the distributions of 14 gene expression phenotypes significantly deviate from normality (Kolmogorov-Smirnov test statistic > 0.8), and these genes were filtered out due to potentially unreliable measurements (Zan et al. 2016). The remaining 5 genes were passed onto eQTL mapping at the discovered locus (see Methods).

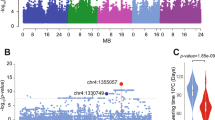
Based on the locus-specific eQTL mapping summary statistics, we applied the recently developed Summary-level Mendelian Randomization (SMR) method (Zhu et al. 2016) to predict potential candidate genes among these five genes. The analysis integrates summary association statistics from GWAS and eQTL scan to predict functional candidate genes using multiple-instrument Mendelian randomization (Burgess et al. 2015), where the complementary HEterogeneity In Dependent Instruments (HEIDI) test checks that the gene expression and flowering time share the same underlying causal variant. One significant candidate AT1G11560 was detected after Bonferroni correction for five tests (Fig. 6, Table 2). This candidate gene prediction result was also replicated using an independent eQTL mapping dataset (Kawakatsu et al. 2016).

Fig. 6: Prioritized candidate genes at the detected locus for flowering time using SMR analysis.
figure 6

a Manhattan plot of the association between the flowering time at 10 °C and SNPs around 40 kb of the top associated SNP in bivariate analysis. The diamonds highlight top eQTL for individual genes. b Manhattan plot of the association between expression of AT1G11560 and SNPs around 40 kb of the top associated SNP in bivariate analysis. Genes tested in SMR analysis are highlighted using arrows. c The linkage-disequilibrium structure at the locus is similar for the corresponding populations in both GWA and eQTL analyses.

Full size image
Table 2 Summary of the SMR/HEIDI analysis results.
Full size table

Indication of co-selection with genes in flowering-related pathways

As flowering time is a well-known polygenic trait, we expect multiple loci to be involved and possibly co-selected as a result of parallel evolution. Therefore, we explored the evidence of co-selection by associating the expression values of 288 known genes in flowering-time-related pathways and one gene in the maturation-related pathway with our top SNP using transcriptome data from 648 A. thaliana accessions (The 1001 Genomes Consortium 2016) (see Methods). In total, six genes (NF-YA8, AT5G53360, SPL15, AGL42, FLC, AGL20) were associated with our top SNP (false discovery rate < 0.05), where, conservatively, four genes (AT5G53360, AGL42, FLC, AGL20) were replicated after Bonferroni correction for six tests using data from an independent collection of 140 A. thaliana(Schmitz et al. 2013) (Supplementary Table S2). This indicates that co-selected genes in multiple pathways determine the flowering time variation in nature, and our detected locus contributes to a part of that.

Discussion

A serious issue of GWAS in natural population is the confounding between true underlying genetic effects and the population structure, which can lead to spurious associations between genotypes and phenotypes if population stratification is not properly adjusted for (Korte and Farlow 2013; Wellenreuther and Hansson 2016; Yang et al. 2014). Incorporation of the random polygenic effect using linear mixed models can effectively control for the population structure, but such correction often compromises the true signals. Here, we applied a bivariate analysis to a classic dataset and successfully separated a locus from the strong population structure. The detected allele is associated with late flowering and slow maturation of A. thaliana, which was corrected away by the linear mixed model in a standard single-trait analysis. The replication of the genetic effect on flowering time in an old intercross linkage analysis and another independent dataset improves the confidence of this association. The discovered association is a typical example that jointly modeling phenotypes that share the genetic basis can boost discovery power and reveal the pleiotropic genotype-phenotype map at the same time.

Together with our recent application of multivariate analysis in human isolated populations (Shen et al. 2017), the results further indicate that multi-phenotype analysis is an effective approach to detect hidden loci that lack discovery power in single-phenotype analysis and thus is worth testing in broader applications. The multivariate analysis appears to have the greatest power when the locus-specific genetic correlation does not agree with the natural phenotypic correlation. For instance, like the discovery here, for two traits that are negatively correlated, loci that generate a positive genetic correlation between the traits tend to have a good chance of being detected in a joint analysis.

In GWAS, phenotypes are usually chosen based on morphological, physiological, or economical features. Those features are usually feasible and simple to quantify; however, they might not be directly representative of the underlying genetic or biological factor that we try to detect. Fortunately, complex traits often share a certain degree of genetic basis, as genetic variants or genes can affect multiple phenotypes, a phenomenon known as pleiotropy (Li et al. 2021; Visscher and Yang 2016; Watanabe et al. 2019). Nowadays, it is very common that multiple phenotypes are measured for the same individuals in many GWAS datasets, especially in omics studies where thousands of phenotypes are measured. Instead of focusing on one phenotype at a time, it is of essential value to jointly model multiple phenotypes, attempting to detect pleiotropic loci that affect multiple traits with biological relevance. Our approach facilitates the identification of genetic loci with combined effects on two traits, regardless of whether the underlying mechanism involves biological pleiotropy or linkage. Namely, we focus on detecting statistical pleiotropy rather than biological pleiotropy, aiming to map loci in the genome that exhibit effects on different traits, even if distinct sites within the same locus regulate each trait. In essence, our mapping strategy identifies loci in the genome that create a genetic correlation between two traits, encompassing both shared biology and shared genetic effects due to linkage.

In this study, all the pairs of traits that are associated with the detected locus contain at least one flowering-time trait, and nearly all of them have maturation duration involved. Detection of the novel locus in a bivariate analysis indicates a shared genetic basis for the two types of developmental traits, which measure the lengths of two important periods during the plant’s lifetime. By integrating the expression level information and GWAS result using the SMR/HEIDI test, we were able to predict candidate genes in this region. However, further work beyond the scope of this paper is still required to establish the molecular biological basis underlying the replicate association.

Many genetic variants affecting flowering time have been mapped, and many genes promoting flowering times have been well characterized using standard laboratory accession, Col-0 (Brachi et al. 2010). Unlike simple traits, where only one or a few alleles are driving the trait’s variation, there are many more variants throughout the genome that contribute to the variation of flowering time (Atwell et al. 2010; Li et al. 2010; Sasaki et al. 2021; The 1001 Genomes Consortium 2016; Zan and Carlborg 2019). The associations between the top SNP in this study and the expression of many flowering-time-related genes serve as evidence of co-selection or parallel adaptation. Additionally, the optimal genetic makeup for complex traits may vary across different environments, highlighting the influence of genotype-by-environment interactions for local adaptation (Baduel et al. 2021; El-Soda et al. 2014). These genotype-by-environment interactions also shape the flowering time of A. thaliana(Ferrero-Serrano and Assmann 2019; Sasaki et al. 2015; Zan and Carlborg 2019). Conducting genotype-by-environment interaction analyses (Li et al. 2022b) for flowering time-related traits in diverse environmental conditions can provide valuable insights for unraveling the intricate genetic architecture of this complex trait (Supplementary Fig. S18).

In conclusion, our study demonstrates the efficiency of joint modeling multiple phenotypes which overcomes severe power loss due to population stratification in association studies. We discover and replicate a pleiotropic allele that regulates flowering and maturation periods simultaneously, providing novel insights into understanding the plant’s development over a lifetime. By integrating gene expression information with the GWAS results, we predict a functional candidate underneath the associated genomic region. We encourage wider applications of such a multivariate framework in future analyses of genomic data. Discoveries from such analysis could suggest crucial genes exhibiting pleiotropic effects. Furthermore, elucidating the functional mechanisms of these genes could unveil new dimensions of biological understanding.