Knee injury prevention via personalized exercise using EDAS method and Sugeno Weber operator under complex q rung orthopair fuzzy data

Multicriteria decision making (MCDM) is the method in which one alternative is selected as the better option among many available alternatives. The citizens will also have to make decisions in many circumstances, highlighting the need to learn skills to make effective decisions. It is a field that has involved several researchers and experts, and relatively several such studies have been undertaken using different methods. In traditional decision-making, there is usually an exact, unambiguous data set. In practice, however, uncertainty introduces a scenario in which data is poorly defined. To resolve this unambiguous Information, Zaded¹ proposed the idea of fuzzy set (FS) theory, which is symbolized by a satisfactory degree (SD) \(\mathop \text A \limits^{.}\left( {\text{o}} \right)\) that allocated between \(\:\left[0,\:1\right]\) and satisfied the condition \(\:0\le\:\mathop \text A \limits^{.}\left( {\text{o}} \right)\le\:1\). This idea has the skill to access data in \(\:\left[0,\:1\right]\). In the decision-making process, FS considers a big revolution to access human ideas accurately. FS theory failed due to a dissatisfactory degree (DSD). It cannot access data if SDS is involved. To address this, Atanassov² gave the notion of DSD to the fuzzy theory and introduced the intuitionistic fuzzy (IFS) concept. This theory contains both SD and DSD lying between \(\:0\) and \(\:1\) and achieved the condition \(0 \le \mathop \text A \limits^{.}\left( {\text{o}} \right) + \mathop \beta \limits^{..} \left( {\text{o}} \right) \le 1\). IFS theory provides a large range of Information for investigating human ideas. Further, many researchers use this idea in the application Khan et al.³ established the idea of circular IF preference relation with group decision making, and Kumar⁴ used IF to selecting stock. Further, many experts give such data of SD and DSD that cannot fulfill the condition \(0 \le \mathop \text A \limits^{.}\left( {\text{o}} \right) + \mathop \beta \limits^{..} \left( {\text{o}} \right) \le 1\), such as \(\:0\le\:0.61+0.66=1.27\nleq\:1\). To address this situation, Yagar⁵ provided the concept of Pythagorean fuzzy set (PyS) theory with the limitation that the \(0 \le {\mathop \text A \limits^{.}}^{2} \left( {\text{o}} \right) + {\mathop \beta \limits^{..}}^{2} \left( {\text{o}} \right) \le 1\) means the square sum of SD \(\mathop \text A \limits^{.}\left( {\text{o}} \right)\) and DSD lies between \(\:0\) and \(\:1\). Even while IFS and PyFS theory accomplished accurately defining ambiguous data, there are still some issues that they cannot handle; many experts give such data of SD and DSD that cannot fulfill the condition of IFS and PyFS theory, such as \(\:0\le\:{0.88}^{2}+{0.69}^{2}=1.2505\nleq\:1\) exceeds \(\:0\) and \(\:1\). To order this problem, To address this situation, Yager⁶ discussed the q-rung orthopair fuzzy set theory (q-ROFS). This theory provides an extensive range as compared to IFS and PyFS theory for ambiguous data such as \(\:0\le\:{\mathop \text A \limits^{.}}^{\text{q}}\left(\text{o}\right)+{\mathop \beta \limits^{..}}^{\text{q}}\left(\text{o}\right)\le\:1\). Farhadinia et al.⁷ investigate the family of similarity measures for q-ROFS, and Dhumras et al.⁸ established an application of green supplier selection using TOPSIS with R-norm q-rung picture fuzzy data and address the application to MCDM. Peng et al.⁹ proposed aggregation operators (AOs) and exponential operators based on q-ROFS and investigated the application with a new score function based on the decision-making process. Still, many scholars consider more advances than before notion, but under some conditions during the decision-making process, the theory, in which he splits the SD in terms of a complex set, where \(\:{\mathop \text A \limits^{.}}\left(\text{o}\right)\in\:\left[0,\:1\right],\:\)and\(\:\:{^{\prime}\Omega }_{\mathop \text A \limits^{.}\left(\text{o}\right)}\in\:\left[0,\:1\right]\), also satisfy the term \(\:0\le\:\left[\mathop \text A \limits^{.}\left(\text{o}\right),\:{^{\prime}\Omega }_{\mathop \text A \limits^{.}\left(\text{o}\right)}\right]\le\:1\). The C-FS is indicated by complex functions such as \(\:\text{E}=\left(\mathop \text A \limits^{.}\left(\text{o}\right).{e}^{2\pi\:i{^{\prime}\Omega }_{\mathop \text A \limits^{.}\left(\text{o}\right)}}\right)\). Buckley¹⁰ proposed a C-FS number. Rahman and Muhammad¹¹ established aggregation operators based on a complex polytopic fuzzy model. Rahman and Muhammad¹² proposed complex polytopic fuzzy AOs and improved decision-making through confidence levels. C-FS theory has more advances than before, but under some conditions during decision-making, C-FS cannot access the data by utilizing complex values. To address this issue, Alkouri and Salleh¹³ proposed the notion of complex IFS (C-IFS), in which he splits the SD and DSD in terms of a complex set, where \(\:\mathop \text A \limits^{.}\left(\text{o}\right)\in\:\left[0,\:1\right],\:\:{^{\prime}\Omega }_{\mathop \text A \limits^{.}\left(\text{o}\right)}\in\:\left[0,\:1\right]\), \(\:\:\mathop \beta \limits^{..}\left(\text{o}\right)\in\:\left[0,\:1\right]\) and \(\:{\Omega}_{\:\mathop \beta \limits^{..}\left(\text{o}\right)}\in\:\left[0,\:1\right]\) also satisfy the term \(\:0\le\:\mathop \text A \limits^{.}\left(\text{o}\right)+\:\mathop \beta \limits^{..}\left(\text{o}\right)\le\:1\) and \(\:0\le\:{^{\prime}\Omega }_{\mathop \text A \limits^{.}\left(\text{o}\right)}+{\Omega}_{\:\mathop \beta \limits^{..}\left(\text{o}\right)}\le\:1\). The C-IFS is indicated by complex function such as, \(\:\text{{\rm d}\kern-2.5pt{\rm b}}=\left\{\left(\mathop \text A \limits^{.}\left(\text{o}\right).{e}^{2\pi\:i{^{\prime}\Omega }_{\mathop \text A \limits^{.}\left(\text{o}\right)}},\:\mathop \beta \limits^{..}\left(\text{o}\right).{e}^{2\pi\:i{\Omega}_{\:\mathop \beta \limits^{..}\left(\text{o}\right)}}\right)\right\}\). Ahmad et al.¹⁴ established an application in decision making problems based on complex intuitionistic hesitant fuzzy data. At some situation the sum of real value of SD and real value of SDS exceed from \(\:1\). To handing the human opinion, Ullah et al.¹⁵ discussed the concept of complex Pythagorean fuzzy set (C-PyFS) where \(\:\mathop \text A \limits^{.}\left(\text{o}\right)\in\:\left[0,\:1\right],\:\:{^{\prime}\Omega }_{\mathop \text A \limits^{.}\left(\text{o}\right)}\in\:\left[0,\:1\right]\), \(\:\:\mathop \beta \limits^{..}\left(\text{o}\right)\in\:\left[0,\:1\right]\) and \(\:{\Omega}_{\:\mathop \beta \limits^{..}\left(\text{o}\right)}\in\:\left[0,\:1\right]\) and also satisfy the term \(0 \le {\mathop \text A \limits^{.}}^{2} \left( {\text{o}} \right) + {\mathop \beta \limits^{..}}^{2} \left( {\text{o}} \right) \le 1\) and \(\:0\le\:{^{\prime}\Omega }_{\mathop \text A \limits^{.}\left(\text{o}\right)}^{2}+{\Omega}_{\:\mathop \beta \limits^{..}\left(\text{o}\right)}^{2}\le\:1\). Because they are more generalized than C-FS and C-IFSs, researchers have a lot of attention. Same problem arises in C-IFS and C-PyFS, when experts offer such kind of data, which cannot fulfill the condition of CIFS and C-PyFS such as \(\:0\le\:{0.81}^{2}+{0.63}^{2}=1.053\nleqq\:1\), \(\:0\le\:{0.82}^{2}+{0.65}^{2}=1.0949\nleqq\:1\) and \(\:0\le\:{0.92}^{3}+{0.71}^{3}=1.137\nleqq\:1\), \(\:0\le\:{0.88}^{3}+{0.77}^{3}=1.138\nleqq\:1\). To resolve these types of problem, Liu et al.¹⁶ proposed the idea of complex q-ring orthopair fuzzy set (C-qROFS) which \(\:\mathop \text A \limits^{.}\left(\text{o}\right)\in\:\left[0,\:1\right],\:\:{^{\prime}\Omega }_{\mathop \text A \limits^{.}\left(\text{o}\right)}\in\:\left[0,\:1\right]\), \(\:\:\mathop \beta \limits^{..}\left(\text{o}\right)\in\:\left[0,\:1\right]\) and \(\:{\Omega}_{\:\mathop \beta \limits^{..}\left(\text{o}\right)}\in\:\left[0,\:1\right]\) and also satisfy the term \(0 \le {\mathop \text A \limits^{.}}^{q} \left( {\text{o}} \right) + {\mathop \beta \limits^{..}}^{q} \left( {\text{o}} \right) \le 1\) and \(\:0\le\:{^{\prime}\Omega }_{\mathop \text A \limits^{.}\left(\text{o}\right)}^{\text{q}}+{\Omega}_{\:\mathop \beta \limits^{..}\left(\text{o}\right)}^{\text{q}}\le\:1\). The C-qROFS is considered by a complex valued function, as \(\:\Phi=\left\{\left(\mathop \text A \limits^{.}\left(\text{o}\right).{e}^{2\pi\:i{^{\prime}\Omega }_{\mathop \text A \limits^{.}\left(\text{o}\right)}},\:\mathop \beta \limits^{..}\left(\text{o}\right).{e}^{2\pi\:i{\Omega}_{\:\mathop \beta \limits^{..}\left(\text{o}\right)}}\right):\:\text{o}\in\:\Upsilon\right\}\). The C-qROFS provided large range from all above discuss notion and more flexible to handling the ambiguity. The comparison table of C-qROFS with other sets is discuss in (Table 1).

Importance of TNM and TCNM operations

In fuzzy set theory, the t-norm (TNM) and t-conorm (TCNM) operations are vital in modeling and managing ambiguous and uncertain data. TNM and TCNM are essential in describing how fuzzy sets relate, mainly in aggregation operations in fuzzy theory and the decision-making process. The Sugeno-Weber TNM and TCNM are significant in C-qROFS due to their flexibility and parameterized environment, which improve decision-making abilities based on complex ambiguity. Sugeno-Weber AOs proposed a parameter \(\:\begin{aligned}{{\rm Q}} \end{aligned}\), which allows for monitoring the collaboration between satisfactory and dissatisfactory degrees. In C-qROFS, in which ambiguity involves phase term and q-ROF limitations, this adaptive allows flexibility modification for different areas, such as risk analysis or personalized decision-making. The complex framework of C-qROFS needs innovative AOs to operate effectively in both magnitude and phase terms. Sugeno-Weber AOs can offer robust techniques for a combination of fuzzy data. It can make them suitable for MCDM when accurate modeling of collaboration properties is essential. Sugeno-Weber operations apply to C-qROFS in fields like Medical diagnosis, Engineering systems, and Risk management. They give a prevailing structure for effectively managing multi-dimensional and phase-based hesitations in real-life problems. Thus, for the first time, the notion of triangular norm was discussed by Manger et al.¹⁷. He used FS theory to provide data scientists and mathematicians with a novel way to aggregate ambiguous data. Next, mathematicians formed several TNM and TCNM operations for various fuzzy contexts. For example, the concept of Dombi AOs for C-qROFS discussed by Ali and Mahmood¹⁸, Sun et al.¹⁹ expressed an AHP model applying PYFS data for MCDM contests, Mandal and Seikh²⁰ investigate Dombi AOs under interval-valued spherical fuzzy MABAC method and Ali²¹ proposed proposed an application for selection of sustainable supplier under spherical fuzzy framework with Aczel-Alsina prioritization. Akram et al.²² give the idea of C-IFS Hamacher TNM and TCNM for decision-making, and Khan et al.²³ using Aczel-Alsina TNM and TCNM for intuitionistic fuzzy rough (IFR) prioritized AOs. To select robots based on IFR TOPSIS expending Einstein AOs presented by Qadir et al.²⁴. We have assumed hypothetical weights for our information. Many other researcher use many AO operator for WV such as Turskis et al.²⁵ used AHP for the selection of construction site selection, Khan et al.²⁶ used Power AOs to find the WV and khan et al.²⁷ used prioritize AOs to calculate the WV. Sugeno established this concept in his PHD thesis. Later on, Weber introduced the idea of Sugeno-Weber TNM and TCNM. Sugeno-Weber triangular norms are flexible and effective aggregation methods used to solve uncertain information about real-life problems in decision-making. For healthcare supply chain management, a group decision-making approach with Sugeno-Weber was introduced by Senapati et al.²⁸. Sugeno-Weber TNM and TCN for spherical fuzzy set and their application in real-life problems proposed by Hussain and Ullah²⁹.

Applications of the EDAS technique in fuzzy set theory

EDAS is a decision-making method that is especially applicable to MCDM problems. EDAS is used to select the best alternative from many providers based on distance from the averaging solution. This technique can handle human judgment and expert opinion. EDAS technique is essential for many real-life problems where human opinion plays a vital role. Using the EDAS technique on IFR for multicriteria group decision-making (MCGDM) proposed by Yahya et al.³⁰. Li et al.³¹. introduced the concept of the EDAS technique for MCGDM based on q-ROF context³¹. and Qiyas et al.³² presented the idea of C-qROF rough Hamacher AOs by the EDAS method. Dhumras and Bajaj³³ proposed a picture of fuzzy soft Dombi AOs and Improved EDAS technique for MCDM in robotic agrifarming. Khan and Wang³⁴ proposed application to decision-making and generalized and group-generalized parameter Fermatean fuzzy AOs.

Importance of case study

According to case studies, personalized knee therapy provides significant benefits of customized exercise plans to the individual. It highlights the significance of a person-centered method, which leads to improved results, decreases the hazard of reinjury, and improves durable usefulness. Clinicians, patients, and researchers benefit significantly from meaningful how personalized exercise exists custom-made following every patient’s specific individuality. This case study investigates how fuzzy theory improves decision-making in customized exercises. Its primary goals are to maximize muscle strength improvement, Cardiovascular Endurance, Recovery Time, and Improvement in flexibility and range of motion. Duong et al.³⁵ proposed the Evaluation and handling of knee pain, prevention, and management of injuries on exercise prescription for exercise and sport science position presented by Beck et al.³⁶ and improve the treatment of sports knee injuries based on personalized exercise prescription presented by Chen et al.³⁷. Plans for the prevention of knee injuries were presented by Roos and Arden³⁸. The study of prevention from knee injuries by physical activities offered by Bendrik et al.³⁹. Figure 1 shows the Knee rehabilitation exercises.

Show the best exercises for the knee. Address: https://www.pinterest.com/pin/remedies--90564642494601249/.

Full size image

Research gap and motivation

We detected that the Sugeno Weber TNM, TCNM, and EDAS methods for C-qROF data were not explored. Nevertheless, the C-qROFS is wider-ranging than some existing ones, such as C-FS, C-IFS, and C-PyFS, and based on Sugeno Weber, TNM TCNM and EDAS are superior to other AOs. So, it is necessary to define a few novel AOs for the C-qROFS environment using the Sugeno Weber TNM, TCNM, and EDAS techniques. Finally, we proposed C-qROFS Sugeno-Weber weighted averaging (C-qROFSWWA) and C-qROF Sugeno-Weber weighted geometric (C-qROFSWWG) aggregation operator and EDAS technique to fill this gap. These tools are advanced tools for decision-making in ambiguous environments. The C-qROFSWWA and EDAS aggregate satisfactory and dissatisfactory degrees in C-qROFS by allocating weight. The C-qROFSWWG calculates Information by multiplication and highlights proportional change while recollecting the impact of individual elements. The operators recognize the C-qROF properties, certifying the sum of power \(\:q\) of satisfactory and dissatisfactory degrees cannot exceed \(\:1\). We applied our work to numerical examples. The main aids of our suggested AOs are described below:

1) if we have put \(\:q=2\) in C-qROFS, our suggested AOs have been changed to C-PyFS.

2) if we have put \(\:q=1\) in C-qROFS, our suggested AOs are changed to C-IFFS.

3) If we have taken \(\:q=2\) and \(\:{^{\prime}\Omega }_{\mathop \text A \limits^{.}\left(\text{o}\right)}={\Omega}_{\:\mathop \beta \limits^{..}\left(\text{o}\right)}=0\) in C-qROFS, our suggested AOs are changed to PyFS.

4) If we take \(\:q=1\) and \(\:{^{\prime}\Omega }_{\mathop \text A \limits^{.}\left(\text{o}\right)}={\Omega}_{\:\mathop \beta \limits^{..}\left(\text{o}\right)}=0\) in C-qROFS, our suggested AOs have been changed to IFS.

Advantages of the proposed method

1. 1.

   The proposed technique is based on C-qROFS, Sugeno Weber, and EDAS operators, expanding decision correctness by taking more ambiguity and imprecision in Knee injury data.

2. 2.

   C-qROFS realistically contracts with vagueness and unsatisfactory data. C-qROFS creates the development suitable for real-world Knee injury healing.

3. 3.

   The Sugeno Weber aggregation operator suggests a more stable aggregation by mutuality among criteria, leading to more dependable decision outcomes.

4. 4.

   EDAS offers a modest and operative way to rank alternatives by associating their distances with an average solution.

5. 5.

   The proposed model is optimal for high-order Knee injury data examination, where numerous criteria should be evaluated.

6. 6.

   The proposed method can apply to numerous real-life applications, such as Environmental Impact Assessment, Artificial Intelligence & Decision Support Systems, Healthcare Decision Making, Supplier or Vendor Selection, and Engineering Design and Evaluation.

Organization of proposed theory

The main structure of this article is as follows: In Sect. 2, we explain previous definitions related to our article and propose the basic idea and concepts, such as the Sugeno Weber based on C-qROFS and their operational laws. In Sect. 3, we propose some aggregation operators, such as C-qROFSWWA and C-qROFSWWG, using C-qROFS, Information corresponding to the operational laws of Sugeno weber TNM and TCN and also discuss some essential properties of these operators. Section 4 uses C-qROFSWWA and C-qROFSWWG operators to investigate the MCDM problem with C-qROF data, using MCDM to solve real-life examples and discuss the EDAS technique and algorithm. In Sect. 5, we compare our suggested operator with various existing operators. In Sect. 6, the Conclusion is discussed.

Preliminaries

Here, we review essential definitions relevant to our articles, such as C-FS, C-IFS, C-PyFS, and C-qROFS, and their laws. Table 2 is for clarification of symbols used in our article.

Definition 1 ⁴⁰

Consider fix set \(\:\Upsilon\), and the C-FS is described on \(\:\Upsilon\) as:

where \(\:\mathop \text A \limits^{.}\left(\text{o}\right)\) and \(\:{^{\prime}\Omega }_{\mathop \text A \limits^{.}\left(\text{o}\right)}\)represented the amplitude and phase term of satisfactory degree (SD), also \(\:\mathop \text A \limits^{.}\left(\text{o}\right),{^{\prime}\Omega }_{\mathop \text A \limits^{.}\left(\text{o}\right)}\in\:\left[0,\:1\right].\) where \(\:i=\sqrt{-1}.\)

Definition 2 ⁴¹

Consider fix set \(\:\Upsilon\), and the C-IFS is described on \(\:\Upsilon\) as follows:

where \(\:\mathop \text A \limits^{.}\left(\text{o}\right)\), \(\:{^{\prime}\Omega }_{\mathop \text A \limits^{.}\left(\text{o}\right)}\), \(\:\mathop \beta \limits^{..}\left(\text{o}\right)\) and \(\:{\Omega}_{\:\mathop \beta \limits^{..}\left(\text{o}\right)}\) represented the amplitude and phase term of SD and dissatisfactory degree (DSD), Also \(\:0\le\:\mathop \text A \limits^{.}\left(\text{o}\right)+\:\mathop \beta \limits^{..}\left(\text{o}\right)\le\:1\), \(\:0\le\:{^{\prime}\Omega }_{\mathop \text A \limits^{.}\left(\text{o}\right)}+{\Omega}_{\:\mathop \beta \limits^{..}\left(\text{o}\right)}\le\:1\) and \(\:\mathop \text A \limits^{.}\left(\text{o}\right),\:{e}^{2\pi\:i{^{\prime}\Omega }_{\mathop \text A \limits^{.}\left(\text{o}\right)}},\:\mathop \beta \limits^{..}\left(\text{o}\right)\) and \(\:{e}^{2\pi\:i{\Omega}_{\:\mathop \beta \limits^{..}\left(\text{o}\right)}}\) from \(\:\left[0,\:1\right]\). Where \(\:i=\sqrt{-1}\). The hesitancy grade is described as \(\:{\updelta\:}=1-\left(\mathop \text A \limits^{.}\left(\text{o}\right)+\:\mathop \beta \limits^{..}\left(\text{o}\right)\right)\) and \(\:{\updelta\:}=1-\left({^{\prime}\Omega }_{\mathop \text A \limits^{.}\left(\text{o}\right)}+{\Omega}_{\:\mathop \beta \limits^{..}\left(\text{o}\right)}\right).\)

Definition 3 ¹⁵

Consider fix set \(\:\Upsilon\), and the C-PyFS is described on \(\:\Upsilon\) as follows:

where \(\:\mathop \text A \limits^{.}\left(\text{o}\right)\), \(\:{^{\prime}\Omega }_{\mathop \text A \limits^{.}\left(\text{o}\right)}\), \(\:\mathop \beta \limits^{..}\left(\text{o}\right)\) and \(\:{\Omega}_{\:\mathop \beta \limits^{..}\left(\text{o}\right)}\) represented the amplitude and phase term of SD and DSD, also \(0 \le {\mathop \text A \limits^{.}}^{2} \left( {\text{o}} \right) + {\mathop \beta \limits^{..}}^{2} \left( {\text{o}} \right) \le 1\), \(\:0\le\:{^{\prime}\Omega }_{\mathop \text A \limits^{.}\left(\text{o}\right)}^{2}+{\Omega}_{\:\mathop \beta \limits^{..}\left(\text{o}\right)}^{2}\le\:1\) and \(\:\mathop \text A \limits^{.}\left(\text{o}\right),\:{e}^{2\pi\:i{^{\prime}\Omega }_{\mathop \text A \limits^{.}\left(\text{o}\right)}},\:\mathop \beta \limits^{..}\left(\text{o}\right)\) and \(\:{e}^{2\pi\:i{\Omega}_{\:\mathop \beta \limits^{..}\left(\text{o}\right)}}\) from \(\:\left[0,\:1\right]\). Where \(\:i=\sqrt{-1}\). The hesitancy degree is defined as \(\:{\updelta\:}=\sqrt{1-\left({\mathop \text A \limits^{.}}^{2} \left( {\text{o}} \right) + {\mathop \beta \limits^{..}}^{2} \left( {\text{o}} \right)\right)}\) and \(\:{\updelta\:}=\sqrt{1-\left({^{\prime}\Omega }_{\mathop \text A \limits^{.}\left(\text{o}\right)}^{2}+{\Omega}_{\:\mathop \beta \limits^{..}\left(\text{o}\right)}^{2}\right)}.\)

Definition 4 ¹⁶

Consider fix set \(\:\Upsilon\); The C-qROFS is described on \(\:\Upsilon\) as follows:

where \(\:\mathop \text A \limits^{.}\left(\text{o}\right)\), \(\:{^{\prime}\Omega }_{\mathop \text A \limits^{.}\left(\text{o}\right)}\), \(\:\mathop \beta \limits^{..}\left(\text{o}\right)\) and \(\:{\Omega}_{\:\mathop \beta \limits^{..}\left(\text{o}\right)}\) represented the amplitude and phase term of SD and DSD, also \(0 \le {\mathop \text A \limits^{.}}^{q} \left( {\text{o}} \right) + {\mathop \beta \limits^{..}}^{q} \left( {\text{o}} \right) \le 1\), \(\:0\le\:{^{\prime}\Omega }_{\mathop \text A \limits^{.}\left(\text{o}\right)}^{\text{q}}+{\Omega}_{\:\mathop \beta \limits^{..}\left(\text{o}\right)}^{\text{q}}\le\:1\) and \(\:\mathop \text A \limits^{.}\left(\text{o}\right),\:{e}^{2\pi\:i{^{\prime}\Omega }_{\mathop \text A \limits^{.}\left(\text{o}\right)}},\:\mathop \beta \limits^{..}\left(\text{o}\right)\) and \(\:{e}^{2\pi\:i{\Omega}_{\:\mathop \beta \limits^{..}\left(\text{o}\right)}}\) from \(\:\left[0,\:1\right]\). Where \(\:i=\sqrt{-1}\). The hesitancy degree is defined as \(\:{\updelta\:}=\sqrt{1-\left({\mathop \text A \limits^{.}}^{q} \left( {\text{o}} \right) + {\mathop \beta \limits^{..}}^{q} \left( {\text{o}} \right)\right)}\) and \(\:{\updelta\:}=\sqrt[q]{1-\left({^{\prime}\Omega }_{\mathop \text A \limits^{.}\left(\text{o}\right)}^{\text{q}}+{\Omega}_{\:\mathop \beta \limits^{..}\left(\text{o}\right)}^{\text{q}}\right)}\). For the easiness, C-qROFS write as \(\left({\mathop \text A \limits^{.}}_{i}.{e}^{2\pi\:i{{^{\prime}\Omega }}_{{\mathop \text A \limits^{.}}_{i}}},\:{\mathop \beta \limits^{..}}_{i}.{e}^{2\pi\:i{\Omega}_{\:{\mathop \beta \limits^{..}}_{i}}}\right)\).

Definition 5 ¹⁶

Consider any sets of C-qROFS, such as \(\:{\Phi}_{i}=\left({\mathop \text A \limits^{.}}_{i}.{e}^{2\pi\:i{{^{\prime}\Omega }}_{{\mathop \text A \limits^{.}}_{i}}},\:{\mathop \beta \limits^{..}}_{i}.{e}^{2\pi\:i{\Omega}_{\:{\mathop \beta \limits^{..}}_{i}}}\right)\), \(\:{\Phi}_{1}=\left({\mathop \text A \limits^{.}}_{1}.{e}^{2\pi\:i{^{\prime}\Omega }_{{\mathop \text A \limits^{.}}_{1}}},\:{\mathop \beta \limits^{..}}_{1}.{e}^{2\pi\:i{\Omega}_{\:{\mathop \beta \limits^{..}}_{1}}}\right)\) and \(\:{\Phi}_{2}=\left({\mathop \text A \limits^{.}}_{2}.{e}^{2\pi\:i{^{\prime}\Omega }_{{\mathop \text A \limits^{.}}_{2}}},\:{\mathop \beta \limits^{..}}_{2}.{e}^{2\pi\:i{\Omega}_{\:{\mathop \beta \limits^{..}}_{2}}}\right)\) with \(\:\gamma>0\). So:

1)

2)

3)

4)

Definition 6 ¹⁶

Consider any set of C-qROFS, such as \(\:{\Phi}_{i}=\left({\mathop \text A \limits^{.}}_{i}.{e}^{2\pi\:i{{^{\prime}\Omega }}_{{\mathop \text A \limits^{.}}_{i}}},\:{\mathop \beta \limits^{..}}_{i}.{e}^{2\pi\:i{\Omega}_{\:{\mathop \beta \limits^{..}}_{i}}}\right)\), the score function \(\:SF\left(\Phi\right)\) and accuracy function \(\:AF\left(\Phi\right)\) defined below:

The score value function measures the overall performance of each alternative by combining its criteria values into a single comparable score. This helps rank alternatives accurately based on multiple criteria.

Definition 7 ¹⁶

Consider any sets of C-qROFS, such as \(\:{\Phi}_{1}=\left({\mathop \text A \limits^{.}}_{1}.{e}^{2\pi\:i{^{\prime}\Omega }_{{\mathop \text A \limits^{.}}_{1}}},\:{\mathop \beta \limits^{..}}_{1}.{e}^{2\pi\:i{\Omega}_{\:{\mathop \beta \limits^{..}}_{1}}}\right)\) and \(\:{\Phi}_{2}=\left({\mathop \text A \limits^{.}}_{2}.{e}^{2\pi\:i{^{\prime}\Omega }_{{\mathop \text A \limits^{.}}_{2}}},\:{\mathop \beta \limits^{..}}_{2}.{e}^{2\pi\:i{\Omega}_{\:{\mathop \beta \limits^{..}}_{2}}}\right)\), the comparison between any C-qROFS is listed following:

1) \(\:SF\left({\Phi}_{1}\right)>SF\left({\Phi}_{2}\right)\), then \(\:{\Phi}_{1}>{\Phi}_{2}\).

2) \(\:SF\left({\Phi}_{1}\right)<SF\left({\Phi}_{2}\right)\), then \(\:{\Phi}_{1}<{\Phi}_{2}\).

3) \(\:SF\left({\Phi}_{1}\right)=SF\left({\Phi}_{2}\right)\), then

1. i)

   \(\:AF\left({\Phi}_{1}\right)<AF\left({\Phi}_{1}\right)\), then \(\:{\Phi}_{1}<{\Phi}_{2}\).

2. ii)

   \(\:AF\left({\Phi}_{1}\right)>AF\left({\Phi}_{1}\right)\), then \(\:{\Phi}_{1}>{\Phi}_{2}\).

3. iii)

   \(\:AF\left({\Phi}_{1}\right)=AF\left({\Phi}_{1}\right)\), then \(\:{\Phi}_{1}={\Phi}_{2}\).

Here, we discussed Sugeno Weber TNM and TCNM and some critical rules based on C-qROFS that are essential for this study.

Definition 8 ⁴²

Sarkar et al.⁴² proposed Sugeno Weber TNM and TCNM described as:

And

Here \(\:{S}_{\rotatebox{180}{\sf F}}\left(\mathcal{I},\mathcal{\:}r\right)\) and \(\:{N}_{\rotatebox{180}{\sf F}}\left(\mathcal{I},\mathcal{\:}r\right)\) represent the drastic TNM and TCNM. Also \(\:{S}_{\beta\:}\left(\mathcal{I},\mathcal{\:}r\right)\) and \(\:{N}_{\beta\:}\left(\mathcal{I},\mathcal{\:}r\right)\) show the sum of TNM and TCNM.

The Sugeno Weber TNM patterns the fuzzy intersection by combining inputs with a flexible parameter that corrects interaction strength. The Sugeno Weber TCNM patterns the fuzzy union permitting for a measured combination of ambiguity across criteria.

Definition 9

Consider any sets of C-qROFS, such as \(\:{\Phi}_{i}=\left({\mathop \text A \limits^{.}}_{i}.{e}^{2\pi\:i{{^{\prime}\Omega }}_{{\mathop \text A \limits^{.}}_{i}}},\:{\mathop \beta \limits^{..}}_{i}.{e}^{2\pi\:i{\Omega}_{\:{\mathop \beta \limits^{..}}_{i}}}\right)\), \(\:{\Phi}_{1}=\left(\mathop \text A \limits^{.}_{1}.{e}^{2\pi\:i{^{\prime}\Omega }_{\mathop \text A \limits^{.}_{1}}},\:\mathop \beta \limits^{..}_{1}.{e}^{2\pi\:i{\Omega}_{\:\mathop \beta \limits^{..}_{1}}}\right)\) and \(\:{\Phi}_{2}=\left(\mathop \text A \limits^{.}_{2}.{e}^{2\pi\:i{^{\prime}\Omega }_{\mathop \text A \limits^{.}_{2}}},\:\mathop \beta \limits^{..}_{2}.{e}^{2\pi\:i{\Omega}_{\:\mathop \beta \limits^{..}_{2}}}\right)\) with \(\:\gamma>0\). Some essential laws based on Sugeno Weber TNM and TCNM are described following:

1)

2)

3)

4)

We proposed some aggregation operators, such as C-qROFSWWA and C-qROFSWWG, using C-qROFS information corresponding to the operational laws of Sugeno Weber TNM explained in definition 9. We have defined some of these operators’ essential properties.

Definition 10

Consider any sets of C-qROFS, such as \(\:{\Phi}_{i}=\left({\mathop \text A \limits^{.}}_{i}.{e}^{2\pi\:i{{^{\prime}\Omega }}_{{\mathop \text A \limits^{.}}_{i}}},\:{\mathop \beta \limits^{..}}_{i}.{e}^{2\pi\:i{\Omega}_{\:{\mathop \beta \limits^{..}}_{i}}}\right)\) \(\:i=1,\:2,\dots\:,\xi\). The C-qROFSWWA operator is described in the following:

Here \(\:{\gamma}_{i}=\left({\gamma}_{1},\:{\gamma}_{2},\dots\:,{\gamma}_{\xi}\right)\) be the weight vector with \(\:{\gamma}_{i}\in\:\left[0,\:1\right]\) and \(\:\sum\:_{i=1}^{\xi}{\gamma}_{i}=1.\)

Theorem 1

Consider any sets of C-qROFS, such as \(\:{\Phi}_{i}=\left({\mathop \text A \limits^{.}}_{i}.{e}^{2\pi\:i{{^{\prime}\Omega }}_{{\mathop \text A \limits^{.}}_{i}}},\:{\mathop \beta \limits^{..}}_{i}.{e}^{2\pi\:i{\Omega}_{\:{\mathop \beta \limits^{..}}_{i}}}\right)\) \(\:i=1,\:2,\dots\:,\xi,\) when we are applied C-qROFSWWA outcome is also C-PyFVs, as:

Proof

Proof of this theorem is given in the appendix.

The C-qROFSWWA Eq. (4) calculates the score by multiplying each value by its assigned weight, summing the outcomes, and allotting by the total weights. It helps reflect the relative importance of each criterion in decision-making.

Theorem 2

Consider any sets of C-qROFS, such as \(\:{\Phi}_{i}=\left({\mathop \text A \limits^{.}}_{i}.{e}^{2\pi\:i{{^{\prime}\Omega }}_{{\mathop \text A \limits^{.}}_{i}}},\:{\mathop \beta \limits^{..}}_{i}.{e}^{2\pi\:i{\Omega}_{\:{\mathop \beta \limits^{..}}_{i}}}\right)\) \(\:i=1,\:2,\dots\:,\xi,\) which implies \(\:{\Phi}_{i}=\Phi.\) So, we have:

Proof

Proof of this theorem is given in the appendix.

Theorem 3

Consider any sets of C-qROFS, such as \(\:{\Phi}_{i}=\left({\mathop \text A \limits^{.}}_{i}.{e}^{2\pi\:i{{^{\prime}\Omega }}_{{\mathop \text A \limits^{.}}_{i}}},\:{\mathop \beta \limits^{..}}_{i}.{e}^{2\pi\:i{\Omega}_{\:{\mathop \beta \limits^{..}}_{i}}}\right)\) and, \(\:{{\overbrace {\Phi}}_{i}}=\left({\overbrace {\mathop \text A \limits^{.}}}_{i}.{e}^{2\pi\:i{\overbrace {{^{\prime}\Omega }}}_{{\mathop \text A \limits^{.}}_{i}}},\:{\overbrace {\mathop \beta \limits^{..}}}_{i}.{e}^{2\pi\:i{\overbrace {\Omega}}_{\:{\mathop \beta \limits^{..}}_{i}}}\right)\) \(\:i=1,\:2,\dots\:,\xi.\) So, \(\:{\Phi}_{i}\ge\:{{\overbrace {\Phi}}_{i}}\) So, we have:

Proof

Proof of this theorem is given in the appendix.

Theorem 4

Consider any sets of C-qROFS, such as \(\:{\Phi}_{i}=\left({\mathop \text A \limits^{.}}_{i}.{e}^{2\pi\:i{{^{\prime}\Omega }}_{{\mathop \text A \limits^{.}}_{i}}},\:{\mathop \beta \limits^{..}}_{i}.{e}^{2\pi\:i{\Omega}_{\:{\mathop \beta \limits^{..}}_{i}}}\right)\) \(\:i=1,\:2,\dots\:,\xi,\) here \(\:{\Phi}^{-}=\left(\text{min}\left({\mathop \text A \limits^{.}}_{i}\right).{e}^{2\pi\:imin\left({{^{\prime}\Omega }}_{{\mathop \text A \limits^{.}}_{i}}\right)},\text{max}\left({\mathop \beta \limits^{..}}_{i}\right).{e}^{2\pi\:imax\left({\Omega}_{\:{\mathop \beta \limits^{..}}_{i}}\right)}\right)\) and \(\:{\Phi}^{+}=\left(\text{max}\left({\mathop \text A \limits^{.}}_{i}\right).{e}^{2\pi\:imax\left({{^{\prime}\Omega }}_{{\mathop \text A \limits^{.}}_{i}}\right)},\text{min}\left({\mathop \beta \limits^{..}}_{i}\right).{e}^{2\pi\:imin\left({\Omega}_{\:{\mathop \beta \limits^{..}}_{i}}\right)}\right),\) we can write

Proof

Proof of this theorem is given in the appendix.

Definition 11

Consider any sets of C-qROFS, such as \(\:{\Phi}_{i}=\left({\mathop \text A \limits^{.}}_{i}.{e}^{2\pi\:i{{^{\prime}\Omega }}_{{\mathop \text A \limits^{.}}_{i}}},\:{\mathop \beta \limits^{..}}_{i}.{e}^{2\pi\:i{\Omega}_{\:{\mathop \beta \limits^{..}}_{i}}}\right)\) \(\:i=1,\:2,\dots\:,\xi\). The C-qROFSWWG operator is described in the following:

Here \(\:{\gamma}_{i}=\left({\gamma}_{1},\:{\gamma}_{2},\dots\:,{\gamma}_{\xi}\right)\) be the weight vector with \(\:{\gamma}_{i}\in\:\left[0,\:1\right]\) and \(\:\sum\:_{i=1}^{\xi}{\gamma}_{i}=1\).

Theorem 5

Consider any sets of C-qROFS, such as \(\:{\Phi}_{i}=\left({\mathop \text A \limits^{.}}_{i}.{e}^{2\pi\:i{{^{\prime}\Omega }}_{{\mathop \text A \limits^{.}}_{i}}},\:{\mathop \beta \limits^{..}}_{i}.{e}^{2\pi\:i{\Omega}_{\:{\mathop \beta \limits^{..}}_{i}}}\right)\) \(\:i=1,\:2,\dots\:,\xi,\) when we can apply C-qROFSWWG outcome is also C-PyFVs, as:

Proof

To prove this theorem, follow all the steps of (Theorem 1).

The C-qROFSWWG multiplies each value raised to the power of its assigned weight. It helps combine ratios or percentages while preserving proportional relationships.

Theorem 6

Consider any sets of C-qROFS, such as \(\:{\Phi}_{i}=\left({\mathop \text A \limits^{.}}_{i}.{e}^{2\pi\:i{{^{\prime}\Omega }}_{{\mathop \text A \limits^{.}}_{i}}},\:{\mathop \beta \limits^{..}}_{i}.{e}^{2\pi\:i{\Omega}_{\:{\mathop \beta \limits^{..}}_{i}}}\right)\) \(\:i=1,\:2,\dots\:,\xi,\) which implies \(\:{\Phi}_{i}=\Phi.\) So, we have:

Proof

To prove this theorem, follow all the steps of Theorem 2.

Theorem 7

Consider any sets of C-qROFS, such as \(\:{\Phi}_{i}=\left({\mathop \text A \limits^{.}}_{i}.{e}^{2\pi\:i{{^{\prime}\Omega }}_{{\mathop \text A \limits^{.}}_{i}}},\:{\mathop \beta \limits^{..}}_{i}.{e}^{2\pi\:i{\Omega}_{\:{\mathop \beta \limits^{..}}_{i}}}\right)\) and, \(\:{{\overbrace {\Phi}}_{i}}=\left({\overbrace {\mathop \text A \limits^{.}}}_{i}.{e}^{2\pi\:i{\overbrace {{^{\prime}\Omega }}}_{{\mathop \text A \limits^{.}}_{i}}},\:{\overbrace {\mathop \beta \limits^{..}}}_{i}.{e}^{2\pi\:i{\overbrace {\Omega}}_{\:{\mathop \beta \limits^{..}}_{i}}}\right)\) \(\:i=1,\:2,\dots\:,\xi.\) So, \(\:{\Phi}_{i}\ge\:{{\overbrace {\Phi}}_{i}}_{i},\) So, we have:

Proof

To prove this theorem, follow all the steps of (Theorem 3).

Theorem 8

Consider any sets of C-qROFS, such as \(\:{\Phi}_{i}=\left({\mathop \text A \limits^{.}}_{i}.{e}^{2\pi\:i{{^{\prime}\Omega }}_{{\mathop \text A \limits^{.}}_{i}}},\:{\mathop \beta \limits^{..}}_{i}.{e}^{2\pi\:i{\Omega}_{\:{\mathop \beta \limits^{..}}_{i}}}\right)\) \(\:i=1,\:2,\dots\:,\xi\), here \(\:{\Phi}^{-}=\left(\text{min}\left({\mathop \text A \limits^{.}}_{i}\right).{e}^{2\pi\:imin\left({{^{\prime}\Omega }}_{{\mathop \text A \limits^{.}}_{i}}\right)},\text{max}\left({\mathop \beta \limits^{..}}_{i}\right).{e}^{2\pi\:imax\left({\Omega}_{\:{\mathop \beta \limits^{..}}_{i}}\right)}\right)\) and \(\:{\Phi}^{+}=\left(\text{max}\left({\mathop \text A \limits^{.}}_{i}\right).{e}^{2\pi\:imax\left({{^{\prime}\Omega }}_{{\mathop \text A \limits^{.}}_{i}}\right)},\text{min}\left({\mathop \beta \limits^{..}}_{i}\right).{e}^{2\pi\:imin\left({\Omega}_{\:{\mathop \beta \limits^{..}}_{i}}\right)}\right)\), we can write

Proof

To prove this theorem, follow all the steps of (Theorem 4).

C-qROFSWWA and C-qROFSWWG operators are used to investigate the MCDM problem with C-qROF data. Assume \(\:L=\left\{{L}_{1},\:{L}_{2},\:\dots\:,{L}_{\xi}\right\}\) \(\:\left(\xi=1,\:2,\dots\:,i\right)\) be the group of alternatives and \(\:\text T=\left\{{\text T}_{1},\:{\text T}_{2},\:\dots\:,{\text T}_{\xi}\right\}\) be the group of criteria. All the attributes with weight vector \(\:{\gamma}_{i}=\left\{{\gamma}_{1},\:{\gamma}_{2},\:\dots\:,{\gamma}_{\xi}\right\}\) with \(\:\sum\:_{i=1}^{\xi}{\gamma}_{i}=1\) and \(\:{\gamma}_{i}\in\:\left[0,\:1\right]\) \(\:\left(\xi=1,\:2,\dots\:,i\right)\). Assume the decision matrix \(\:W={\left({\Phi}_{L\text T}\right)}_{x\times\:y}\), take \(\:{\Phi}_{i}=\left({\mathop \text A \limits^{.}}_{i}.{e}^{2\pi\:i{{^{\prime}\Omega }}_{{\mathop \text A \limits^{.}}_{i}}},\:{\mathop \beta \limits^{..}}_{i}.{e}^{2\pi\:i{\Omega}_{\:{\mathop \beta \limits^{..}}_{i}}}\right)\) represent the C-qROFVs, \(\:{\mathop \text A \limits^{.}}_{i}\) and \(\:{e}^{2\pi\:i{{^{\prime}\Omega }}_{{\mathop \text A \limits^{.}}_{i}}}\) denotes the amplitude and phase term of SD of alternatives and \(\:{\mathop \beta \limits^{..}}_{i}\) and \(\:{e}^{2\pi\:i{\Omega}_{\:{\mathop \beta \limits^{..}}_{i}}}\) denotes the amplitude and phase term of the DSD of alternatives. Now, we can build a decision matrix in the arrangement:

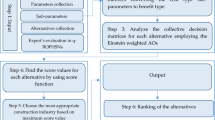
In this decision matrix, \(\:\left(\mathop \text A \limits^{.}_{xy}.{e}^{2\pi\:i{^{\prime}\Omega }_{\mathop \text A \limits^{.}_{xy}}},\:\mathop \beta \limits^{..}_{xy}.{e}^{2\pi\:i{\Omega}_{\:xy}}\right)\) be the C-qROFVs. Next, we can apply our introduced C-qROFSWWA and C-qROFSWWG operators to find the best alternatives in real-life problems. For this resolve, we can use the algorithm defined in (Fig. 2):

Figure 2 shows the algorithm to select the best alternative by assessing numerous criteria through fuzzy aggregation techniques. The procedure starts by gathering Information and applying the C-qROFSWWA and C-qROFSWWG operators to account for uncertainty. Finally, the score function ranks the alternatives and identifies the one with the highest score.

Algorithm for the selection of best alternative.

Full size image

Step 1. Generally, all data about an attribute is divided into beneficial and non-beneficial types. Before the aggregation procedure, we must change all the data to the same type by normalizing the decision matrix using the following formula.

Step 2. We can use our suggested C-qROFSWWA and C-qROFSWWG operators to aggregate the decision matrix. We take parameters in our article \(\:q=3\) and \(\:\begin{aligned}{{\rm Q}} \end{aligned}=2\) for both C-qROFSWWA and C-qROFSWWG.

Step 3. In this step, use definition 5 to calculate the score value.

Step 4. Rank all the score values to select the better alternative.

Step 5. End.

Case study

The algorithm for choosing the best alternative is highly essential in the framework of personalized exercise prescription for preventing knee injury because it certifies that decisions are created based on individualized criteria such as the level of muscle strength improvement, Cardiovascular Endurance, Recovery Time, and Improvement in flexibility and range of motion. By using advanced fuzzy combination approaches like the C-qROFSWWA, C-qROFSWWG, and the EDAS technique, the algorithm can handle the hesitation and inconsistency inherent in human health data. This leads to more accurate and personalized exercise prescriptions, vital for effectively preventing knee injuries in diverse populations.

Knee injuries are common in sportspersons, older adults, and biomechanical situations. Personalized exercise prescriptions approach avoiding these injuries by modifying activities and therapy for each person’s needs. In the following, four doctors provide complete awareness of how tailored exercise strategies, a key component of personalized exercise, can help avoid knee injuries.

Orthopedic surgeon

Orthopedic surgeons point out that the most important cause of knee injuries can be muscle imbalances, mainly in the hamstrings and quadriceps. A personalized exercise plan provides defensive exercises for these muscles. Personalized exercise meaningfully decreases the risk of knee problems. Muscle strengthening around the knee joint is vital. However, balance is equally significant. Numerous People ignore their hamstrings and overdevelop their quadriceps, leading to injury and uncertainty. An experienced establishment plan can prevent this imbalance.

Physical therapist

Physical Therapists highlight that preserving full knee mobility and flexibility is essential for preventing knee injuries, mostly in older people or pre-existing knees. If muscles such as calves and hip flexors are tight and muscles have less flexibility, it causes knee injuries in movement. Mobility and flexibility exercises prevent long-lasting injuries. He offered hip flexor stretches and a regular calf regimen to keep the knee joint flexible, tied with low-impact movements and hamstring.

Sports medicine specialist

The Sports Medicine Specialist technique is based on proprioception, the body’s ability to sense action, movement, and ___location. The possibility of knee injuries will increase if there is a Loss of proprioception, mostly in sportspersons. Incorporating exercise control can immensely lower the risk of knee injuries and anterior cruciate ligament. A personalized exercise strategy should include drills that challenge balance and coordination. He advises participants on plyometrics, agility drills, and single-leg balance exercise training.

Rheumatologist

The rheumatologist highlights that if a person has extra weight, it puts more stress on the knee joint and increases the risk of injury. To solve this problem, personalized exercise is vital in reducing weight. Each extra weight puts more stress on joints, and injury problems will be increased. To reduce the pressure on the knee joint, he provides exercise plans for losing weight, depth training, and management plans to avoid knee injuries. He offered low-impact exercise plans such as aquatic therapy, walking, or riding for people who are overweight. Strength training also helps the knee joint without extra joint burden.

Experimental case study

In this section, MCDM approaches help to select the optimal exercise prescription from different alternatives evaluated across criteria. The MCDM method of handling human doubt and medical data is essential in decision-making. This real-life problem considers four alternatives. \(\:L=\left\{{L}_{1},\:{L}_{2},\:\dots\:,{L}_{\xi}\right\}\) Listed below:

\(\:{L}_{1}\) =Balance and proprioception exercises

An unbalanced body and unstable movements cause the injuries. Proprioception and balance help prevent knee injuries. Proprioception helps the body retain its proper position during movement. Good balance decreases the possibility of falling, which can cause stress in the knee muscles. For this purpose, exercises are balance bean, stability disc, Bosu ball, dynamic stability, single-leg stands, and agility exercise. It helps muscle around the knee and prevents knee injuries. Balance and joint stability are beneficial for both older adults and sportspersons. Figure 3 Show the exercise for Balance and proprioception exercises.

Show the best position for balance and proprioception. Address: https://www.athletescare.com/chiropractors-toronto-blog/the-benefits-of-balance--proprioception~7.html.

Full size image

\(\:{L}_{2}\)=Flexibility and stretching routines

Enhancing the extensibility of your knee cases makes the tissues less stiff, and, in turn, more excellent motion is integrated into that joint. Flexible systems ensure that the knees can operate and not risk any harm through their range of motion. Flexible muscles and position provide a full range of motion without stress on the knee. For this purpose, exercises such as static stretching, hip flexor and calf stretches, and dynamic stretching: lunges with a twist, Leg swings, walking knee hugs, and foam rolling support muscle tightness and flexibility in tissue. It decreases the risk of acute injuries. Figure 4 shows the flexibility and stretching routines exercise.

Show the best position for flexibility and stretching routine exercises. Address: https://www.pinterest.com/pin/408420259941298172/.

Full size image

\(\:{L}_{3}\)=Aerobic conditioning with low-impact activities

Improve muscle strength and cardiovascular health while, at the same time, decreasing the stress on the knee joint by low-impact activities. Aerobic conditioning improves cardiovascular and blood flow, which can help people recover from injuries. It can also help individuals prevent injuries to the knee. For this purpose, exercises include elliptical training, cycling, walking, elliptical training, Aquatic exercises, and rowing. These exercises support strengthening muscles, and during long activities, they support and stabilize the knee joint. Figure 5 shows the best Aerobic conditioning with low-impact activities.

Show the best exercise aerobic conditioning with low-impact activities. Address: https://www.vhwellfit.com/blog/6-low-impact-workouts-to-ease-arthritis-symptoms/.

Full size image

\(\:{L}_{4}\)=Strength training focused on quadriceps and hamstrings

Strength training improves the stability of knee joints by quadriceps and hamstrings. During movement, the quadriceps support the knee joint, and the hamstrings stabilize the knee joint. The weak muscles cause injuries to the knee joint, especially during sudden direction changes when jumping and running. The quadriceps and hamstrings help to reduce the risk of knee injuries. For this purpose, glute bridges, deadlifts, squats, step-ups, leg presses, and lunges are exercises. It helps muscles around the knee and reduces the stress on the knee joint. If these exercises are done incorrectly and without proper balance between the quadriceps and hamstrings, they cause knee injuries. Figure 6 show the Strength training focused on the quadriceps and Fig. 7 Show the top ten hamstring exercises.

Show the best exercise for a quadriceps strain. Address: https://www.facebook.com/Physiocity1/posts/quadriceps-strain-exercise-physio-physiocity-physiotherapy-physicaltherapist-pt-/166009994872671/.

Full size image

Show the top ten exercises for the hamstring. Address: https://www.facebook.com/IamPhysiotherapy/posts/great-post-by-bretcontreras1-here-are-my-top-ten-favorite-hamstring-exercises-ho/2225858590837123/.

Full size image

The mentioned four types of personalized exercise are assessed across four criteria, which are listed following:

1. 1)

   \(\:\text T_{1}=\) level of muscle strength improvement

2. 2)

   \(\:\text T_{2}=\) cardiovascular endurance

3. 3)

   \(\:\text T_{3}=\) recovery time

4. 4)

   \(\:\text T_{4}=\) improvement in flexibility and range of motion

C-qROF presents the principles related to all alternatives and criteria by weight vector allocated to all requirements to show the importance of the requirements. The expert gives \(\:0.31\) weight to the level of muscle strength improvement, \(\:0.28\) to Cardiovascular Endurance, \(\:0.22\) to Recovery Time, and \(\:0.19\) to flexibility and range of motion improvement. The AOs calculate the total fuzzy performance for each biometric authentication method.

The decision matrix for the experimental case study is shown in (Table 3), and all values are C-qROFVs.

Step 1. Generally, all data about an attribute is divided into beneficial and non-beneficial types. However, in this experimental case study, all attributes are beneficial.

Step 2. We used our suggested C-qROFSWWA and C-qROFSWWG operators to aggregate the decision matrix. All aggregated values are shown in (Table 4).

Step 3. Use Eq. (1) to calculate the score value. All calculated score values are displayed in Table 5 Also, a graphical representation of the score value is shown in (Fig. 8).

Step 4. Ranking all the score values to select the better alternative. The ranking is shown in (Table 6).

Graphically representation of score value.

Full size image

Figure 8 shows that the highest ranking is \(\:{L}_{4}\) alternatives by using C-qROFSWWA and C-qROFSWWG. Also, in (Table 6), the highest score value is \(\:{L}_{4}\) alternatives. So, \(\:{L}_{4}\) is the best alternative of all alternatives.

EDAS method

Keshavarz Ghorabaee et al.⁴³ presented the EDAS technique for multicriteria inventory. The following step is used for the EDAS technique to select the best alternative by distance averaging.

Step 1. First, some essential criteria for the selection of alternatives must be chosen.

Step 2. Construct decision matrix \(\:W={\left({\Phi}_{L\text T}\right)}_{x\times\:y}\), take \(\:{\Phi}_{i}=\left({\mathop \text A \limits^{.}}_{i}.{e}^{2\pi\:i{{^{\prime}\Omega }}_{{\mathop \text A \limits^{.}}_{i}}},\:{\mathop \beta \limits^{..}}_{i}.{e}^{2\pi\:i{\Omega}_{\:{\mathop \beta \limits^{..}}_{i}}}\right)\) represent the C-qROFVs, \(\:{\mathop \text A \limits^{.}}_{i}\) and \({e}^{2\pi\:i{{^{\prime}\Omega }}_{{\mathop \text A \limits^{.}}_{i}}}\) denotes the amplitude and phase term of SD of alternatives and \(\:{\mathop \beta \limits^{..}}_{i}\) and \(\:{e}^{2\pi\:i{\Omega}_{\:{\mathop \beta \limits^{..}}_{i}}}\) denotes the amplitude and phase term of the DSD of alternatives. Now, we have built a decision matrix in the arrangement:

In this decision matrix, \(\:\left(\mathop \text A \limits^{.}_{xy}.{e}^{2\pi\:i{^{\prime}\Omega }_{\mathop \text A \limits^{.}_{xy}}},\:\mathop \beta \limits^{..}_{xy}.{e}^{2\pi\:i{\Omega}_{\:xy}}\right)\) be the C-qROFVs. Next, we can apply the EDAS method to find the best alternatives for real-life problems.

Step 3. To find the averaging solution \(\:G\) we can use the C-qROFSWWA operator for all criteria, as displayed below:\(\:{\gamma}_{i}=\left({\gamma}_{1},\:{\gamma}_{2},\dots\:,{\gamma}_{\xi}\right)\) be the weight vector, and the expert gives \(\:0.31\) weight to the level of muscle strength improvement, \(\:0.28\) to Cardiovascular Endurance, \(\:0.22\) to Recovery Time, and \(\:0.19\) to flexibility and range of motion improvement.

This proposed aggregation operator is used to find the averaging solution.

Step 4. In this step, we have computed the positive distance from averaging \(\:J_{xy}\) and negative distance from averaging \(\:P_{xy}\), based on criteria (benefit and non-benefit type), displayed in the following:

For benefit type

If the criteria are beneficial, we used the above equation to find the positive and negative distance from averaging.

For non-benefit type

We used the above equation to find the positive and negative distance from averaging if the criteria are non-benefit.

Step 5. In this step, we can calculate the weighted sum \(\:D_{L}\) of the positive distance from averaging \(\:{\gamma}_{xy}\) and weight sum \(\:R_{L}\) of negative distance from averaging \(\:P_{xy}\) for given alternatives and \(\:{\gamma}_{i}=\left({\gamma}_{1},\:{\gamma}_{2},\dots\:,{\gamma}_{\xi}\right)\) be the weight vector with \(\:{\gamma}_{i}\in\:\left[0,\:1\right]\) and \(\:\sum\:_{i=1}^{\xi}{\gamma}_{i}=1\), display as below:

By using the equation of step 5, we found the weighted sum. \(\:D_{L}\) of the positive distance from averaging \(\:J_{xy}\) and weight sum \(\:R_{L}\) of negative distance from averaging \(\:P_{xy}\).

Step 6. Now, the value of \(\:J_{xy}\) and \(\:P_{xy}\) Normalize for given alternatives, display as below:

By using this equation to normalize the \(\:J_{xy}\) and \(\:P_{xy}\).

Step 7. Find the appraisal score (APS) value for given alternatives, display as below:

Using this equation, find the appraisal score value for all alternatives. The score value is used to find the ranking of other options.

Step 8. Ranking all the alternatives to use values of APS. The alternative with the highest APS value is the best.

We can apply all the steps in the experimental case study to find the best alternatives.

Step 1. First, choose some essential criteria such as level of muscle strength improvement, Cardiovascular Endurance, Recovery Time, and Improvement in flexibility and range of motion to select alternatives.

Step 2. The decision matrix for the experimental case study is shown in (Table 3), and all values are in C-qROFVs.

Step 3. To find the averaging solution \(\:G\) we have used the C-qROFSWWA operator for all criteria, and the aggregated value is displayed below:

Step 4. In this step, we can compute the positive distance from averaging \(\:J_{xy}\) and negative distance from averaging \(\:P_{xy}\) Aggregated values are shown in (Tables 7 and 8).

Step 5. In the following, we can calculate the weighted sum \(\:D_{L}\) of the positive distance from averaging \(\:J_{xy}\) and weight sum \(\:R_{L}\) negative distance from averaging \(\:P_{xy}\) For given alternatives. All calculated data of weighted sum \(\:D_{L}\) of the positive distance from averaging are displayed in Table 9 and weight sum \(\:R_{L}\) negative distance from averaging (Table 10).

Step 6. Now, the value of \(\:J_{xy}\) and \(\:P_{xy}\) normalize

\(\:{\varvec{\Lambda}}_{L}\) and \(\:{\varvec{\Lambda}N}_{L}\) for given alternatives, Shown in (Table 11):

Step 7. Find the appraisal score (APS) value for given alternatives. The aggregated values of APS are shown in (Table 12). The graphical representation of APS is in (Fig. 9).

Graphically representation of APS values by using the EDAS method.

Full size image

Step 8. Ranking all the alternatives to use values of (Table 12). The alternative with the highest APS value is the best. To see in (Table 13).

Table 13 shows that \(\:{L}_{4}\) has the highest APS value, so, \(\:{L}_{4}\) is the best alternatives.

By using EDAS method, C-qROFSWWA and C-qROFSWWG AOs \(\:{L}_{4}\) is the best alternative.

To dissimilarity the suggested method and some existing methods under C-qROFS framework, a relationship analysis was accomplished with different techniques such as complex q-rung orthopair fuzzy Hamacher weighted averaging (C-qROFHWA) and as complex q-rung orthopair fuzzy Hamacher weighted geometric (C-qROFHWG) proposed by Mahmood and Ali⁴⁴, as complex q-rung orthopair fuzzy Yager weighted averaging (C-qROFYWA) and as complex q-rung orthopair fuzzy Yager weighted geometric (C-qROFYWG) proposed by Wu et al.⁴⁵ and complex q-rung orthopair fuzzy weighted averaging (C-qROFWA) and as complex q-rung orthopair fuzzy weighted geometric (C-qROFWG) proposed by Liu et al.¹⁶. Ali and Mahmood⁴⁶ proposed complex q-rung orthopair fuzzy Dombi weighted averaging (C-qROFDWA) and complex q-rung orthopair fuzzy Dombi weighted geometric. Raja et al.⁴⁷ N-soft q-rung orthopair fuzzy N-soft weighted averaging (q-ROFNSWA) and weighted geometric (q-ROFNSWG) cannot be applied to C-qROFS because they cannot handle the complex numbers, phase terms. Their more straightforward framework is unsuitable for modeling the multi-dimensional and directional ambiguities that C-qROFS addresses. Yang et al.⁴⁸ proposed complex intuitionistic fuzzy frank weighted averaging (CIFFWA) and weighted geometric (CIFFWG) cannot aggregate the c-qROFS, and weighted geometric (CIFFWG) cannot aggregate the c-qROFS and the sum of SFD and DSFD increase from \(\:1\). The acquired aggregated values are displayed in (Table 14). This table shows that the values evaluated by the suggested approach and existing approach matched with each other have the same result. However, the geometrical representation of the weighted averaging outcome is displayed in (Fig. 10), and the weighted geometric outcome is displayed in (Fig. 11).

The C-qROFS with the Sugeno-Weber AO and the EDAS technique offer a powerful and flexible context for handling complex decision-making problems. C-qROFS allocates for comfortable illustrating ambiguity through both q-rung flexibility and complex-valued satisfactory, catching amplitude and phase material that traditional fuzzy framework cannot. The Sugeno-Weber operator improves the combination process by adjusting the level of compromise between criteria based on expert boldness. The EDAS method effectually ranks alternatives by assessing their distances from an average solution, since both positive and negative deviations. This hybrid model not only expands the accuracy and strength of the decision-making method but also proves superior presentation through statistical justification, with high association with expert decisions, stable sensitivity behavior, and reduced vagueness in final results.

Graphically representation of weighted averaging by comparative analysis.

Full size image

Graphically representation of weighted geometric by comparative analysis.

Full size image

Sensitivity analysis of parametric

To investigate the impact of parametric values on our suggested model by the changing of parameters \(\:{\begin{aligned}{{\rm Q}} \end{aligned}}\) and \(\:q\). In the framework of personalized exercise prescription for knee injury prevention, this examination helps control the strength of the technique by displaying how sensitive the rankings of exercise alternatives are to slight variations in expert decision ambiguity. We take various parametric values \(\:{\begin{aligned}{{\rm Q}} \end{aligned}}\) and \(\:q\) to investigate the outcomes of finding the ranking of alternatives by using C-qROFSWWA and C-qROFSWWG operators. All outcomes taken by the C-qROFSWWA and C-qROFSWWG operators are displayed in (Tables 15 and 16). The ranking of alternatives is the same when we applied C-qROFSWWA and C-qROFSWWG. The ranking of alternatives \(\:{L}_{4}>{L}_{3}>{L}_{2}>{L}_{1}\) cannot change. alternative \(\:{L}_{4}\) be the best in all rankings. So, the selection of parameter value depends on the expert. All the aggregated values using C-qROFSWWA and C-qROFSWWG with different parameters are shown in (Figs. 12 and 13).

Graphically representation of weighted averaging by sensitivity analysis.

Full size image

Graphically representation of weighted geometric by sensitivity analysis.

Full size image

Practical implementation

We explain how C-qROFSWWA and C-qROFSWWG operators could be implemented in each area mentioned, focusing on practical application.

Engineering design and evaluation

In the engineering design and evaluation framework, implementing the C-qROFSWWA and C-qROFSWWG operators includes aggregating various criteria, such as cost, material strength, durability, and environmental impact, all of which might have uncertain or fuzzy values. Engineers usually work with subjective expert estimations about the performance of different materials or systems. The implementation starts by allocating fuzzy values to various suggested criteria based on expert decisions, such as moderately robust, highly efficient, and suitable cost. These fuzzy values are aggregated using our proposed operators, C-qROFSWWA and C-qROFSWWG operators, which combine the criteria into a final ranking for each alternative design. This proposed aggregation operator is used to handle the non-linear trade-offs between criteria, such as balancing cost with performance. This allows engineers to study multiple trade-offs simultaneously, helping to choose the best design that fits within the fuzzy limitations and goals of the project.

Supplier or vendor selection

In the supplier or vendor selection procedure, the C-qROFSWWA and C-qROFSWWG operators can be implemented to combine multi-criteria assessments from numerous stakeholders or departments, such as procurement teams, technical experts, and even end-users. Initially, each supplier is evaluated across various fuzzy criteria: delivery reliability, product quality, price competitiveness, and service flexibility. These valuations are stated in fuzzy terms and allocated membership functions to characterize uncertainty or partial truth. Applying the C-qROFSWWA and C-qROFSWWG operators, these fuzzy assessments are combined as expert input and each criterion’s relative importance. This permits the organization to rank suppliers based on a comprehensive, fuzzy decision-making process that accounts for both subjective judgments and objective criteria, ultimately leading to a more informed and well-rounded selection process. This proposed technique is particularly valuable when dealing with suppliers from different regions with varying levels of reliability, experience, and risk.

Healthcare decision making

In healthcare decision-making, the C-qROFSWWA and C-qROFSWWG operators can be helpful in patient diagnosis, treatment planning, or resource allocation. For instance, when diagnosing a patient with numerous symptoms that may exist with multiple ambiguity levels, medical experts could evaluate the probability of certain diseases with fuzzy assessments. The established operators C-qROFSWWA and C-qROFSWWG aggregate these fuzzy valuations to find more reliable and inclusive diagnoses or treatment recommendations. In treatment planning, where factors such as patient age, health conditions, and preferences come into play, this proposed technique can help combine clinical Information with expert assessments of treatment usefulness and risks. By managing ambiguity and imprecision in medical data, the explained operator simplifies personalized treatment strategies that explain numerical Information and subjective expert ideas. Our proposed technique is beneficial when there are no straightforward results and decisions must be made based on numerous criteria that relate to each other in complex ways.

Environmental impact assessment

In the Environmental Impact Assessment, the C-qROFSWWA and C-qROFSWWG operators combine expert assessments of various ambiguous or unclear environmental criteria, such as air quality, noise pollution, and ecological disruption. These criteria are often evaluated using fuzzy terms like moderate or low impact. The proposed operator combines these fuzzy inputs while seeing the importance of each criterion, giving a comprehensive impact score. This helps experts assess the overall environmental effects of a project more accurately, especially when data is undeveloped or subjective.

Artificial intelligence & decision support systems

In Artificial Intelligence and Decision-Support Systems, the C-qROFSWWA and C-qROFSWWG operators combine ambiguous and fuzzy data from sources like sensors, user preferences, or contextual inputs. It helps Artificial Intelligence systems make smarter, human-like decisions, such as adjusting smart home settings and choosing safe routes for autonomous vehicles, by effectively managing unclear or vague data and corresponding multiple criteria.

MCDM is an excellent approach for the assessment of uncertain and fuzzy data. Investigating complicated data based on decision-making problems is challenging in the age of advancement. For example, personalized exercise prescription plays an essential role in preventing knee injuries by addressing individual variations in biomechanical and physiological features. In decision-making sciences, the theory of C-qROFS data is extremely valuable and dominant because it is the extended form of fuzzy sets. It covers the satisfactory and dissatisfactory degrees, and the sum of both degrees lies in unit intervals. Also, geometric averaging, Sugeno-weber, and EDAS aggregation operators are constructive and helpful for showing doubtful and ambiguous data in real-life problems. In this article, we have introduced the Sugeno Weber operational laws based on C-qROFS. We have developed the C-qROFSWWA and C-qROFSWWG operators and proposed their properties. Then, we illustrated the decision-making procedure based on the C-qROFS and discussed an algorithm to solve the MCDM problem. Also, we have provided a numerical example to explain the decision-making process based on the proposed C-qROFSWWA and C-qROFSWWG operators. Then, we conduct a deep comparative study with the existing aggregation operator to check the suggested technique’s superiority and validity.

Limitations

Our theory of C-qROFS is extended into numerous structures. The C-qROFS is more advanced than FS, IFS and PyFS, but in several challenges, the C-qROFS framework is unsuccessful in controlling big data. Some restrictions and limitations exist in our work. The C-qROFS cannot operate on picture, spherical, and t-spherical fuzzy sets because abstinence degree cannot be involved in C-qROFS. If the expert gives data in the form of satisfactory, dissatisfactory, and abstinence degrees, then our proposed operator cannot aggregate the data. If the abstinence degree is zero, then the proposed operators are applied.

Future work

In the future, we shall change the C-qROFSs into rough sets, soft sets, complex hesitant q-ROFSs, Complex picture FS, complex spherical FS, and Complex t-spherical FS. We shall cover the idea of the Muirhead mean proposed by Liu et al.⁵⁰. Dhumras et al.⁵¹ established an Application in the Field of Pattern Recognition based on similarity measures of complex picture fuzzy information. The above notion of C-qROFSs can be offered in numerous mathematics fields and can be changed into different mathematical frameworks to explain uncertainty and ambiguity. Some more extensions are presented as we have extended the C-qROF structure into the guideline of exercise for health Almarcha et al.⁵², health promotion system by Sun et al.⁵³. Sharma et al.⁵⁴ established an application for the banking site selection problem. Riaz and Farid⁵⁵ established Linear Diophantine Fuzzy Soft-Max AOs for improving Green Supply Chain Efficiency, Dhumras et al.⁵⁶ proposed electronic marketing strategic plans based on federated learning-oriented q-rung picture fuzzy TOPSIS/VIKOR decision-making method, Hadzikadunic et al.⁵⁷ proposed the logistics performance index of European Union Countries using the Bonferroni operator.