Introduction

Cell heterogeneity is a fundamental characteristic of the tissue microenvironment and plays a key role in physiological and pathological processes1. Accurate identification of cell types is a crucial step in understanding cell heterogeneity and serves as the foundation for downstream analyses. With the development of single-cell sequencing and spatial omics sequencing technologies, we can use clustering analysis methods to categorize cells in tissues into different clusters based on their molecular characteristics. These advanced techniques enable us to systematically reveal the distribution patterns of cells within tissues and their potential biological significance2.

The advancement of single-cell sequencing techniques has enabled the simultaneous analysis of multiple molecular modalities, including mRNA, chromatin accessibility, and DNA methylation, within individual cells3. Compared to single-cell mono-omics data, single-cell multi-omics data provide a more comprehensive view of cellular heterogeneity, offering valuable insights into the complexity of biological systems4,5,6. Different omics data provide complementary insights on cells and their microenvironments. For example, transcriptomics focuses on gene transcription levels, including mRNA and non-coding RNA, reflecting the gene expression status of cells. Proteomics analyzes the composition, abundance, modifications, and interactions of proteins, elucidating protein functions. Metabolomics investigates the types and quantities of small molecular metabolites within cells, reflecting the metabolic state of cells and their responses to environmental stimuli. Epigenomics, on the other hand, explores DNA methylation, histone modifications, and chromatin accessibility, revealing the regulatory mechanisms of gene expression. However, relying solely on single-omic data often fails to comprehensively and accurately capture the subtle differences and heterogeneity among cells.

Researchers have developed various computational methods for clustering multi-omics data, which can be broadly categorized into traditional methods and deep learning-based methods. Traditional methods primarily rely on statistical models for modeling. For example, MOFA+ is a statistical framework designed for integrating single-cell multimodal data, using variational inference to reconstruct low-dimensional representations of the data, thereby enabling joint modeling of variations across multiple sample groups and data modalities7. Seurat v5 leverages graph theory to connect cells with similar patterns by learning cell-specific weights, constructing a weighted nearest-neighbor graph to achieve multi-omics data fusion8. Other traditional methods include GRMEC-SC9 and Mowgli10. On the other hand, deep learning has emerged as a powerful tool for integrating multi-omics data. For instance, totalVI uses a modeling strategy similar to scVI11 to integrate CITE-seq data, which encompasses both RNA and cell surface protein information, providing a comprehensive and scalable framework for multi-omics data integration through variational inference12. MultiVI integrates multimodal information from single-cell transcriptomics, chromatin accessibility, and other molecular characteristics based on deep generative modeling principles, creating a joint latent space for paired and unpaired samples13. scMIC integrates cell attribute information and structural relationships between cells from both local and global perspectives based on deep multi-level information fusion principles, reducing redundant information between different omics at the cellular and feature levels14. Other deep learning-based methods for multi‑omics data integration include scMDC15, BABEL16, and scMM17. However, these methods are designed for single-cell multi-omics data and overlook the crucial spatial information related to tissue structure and the microenvironment context.

Spatial ___location information plays a critical role in cell type identification, as cells of the same type often exhibit specific spatial distribution patterns closely related to particular functional domains18. These spatial distribution patterns, known as spatial domains, are regions within a tissue where cells with similar molecular profiles and functions are spatially organized19,20. Spatial domains can reflect the functional states of cells and their interactions within the tissue microenvironment. For example, in the immune microenvironment, the spatial distribution patterns of different immune cell subpopulations may directly reflect their functional states. Compared to single-cell sequencing technology, spatial multi-omics sequencing integrates molecular profiles with spatial ___location, enabling researchers to investigate cellular heterogeneity within the spatial context of tissues21. Currently, various technologies can simultaneously measure spatial multi-omics data on the same tissue section, such as DBiT-seq22, CUT&Tag-RNA-seq23, SPOTS24, MERSCOPE25, and Nanostring CosMx26. Recently, various computational methods have been developed for cell clustering and spatial ___domain identification in spatial multi-omics data. For example, SpatialGlue uses graph neural networks with dual attention mechanisms to integrate data modalities and reveal histologically relevant structures27. PRAGA uses dynamic graphs and prototype contrastive learning for spatial data integration28. COSMOS utilizes graph neural networks to extract complementary information from two omics, enabling the integration of spatial multi-omics data to identify spatial domains29. MISO can integrate multiple modalities from various spatial omics datasets and serves as a versatile algorithm for feature extraction and clustering30. However, despite the progress made by these methods, finding a single approach that consistently performs well across all scenarios remains challenging. While ensemble learning shows promise for improving algorithm performance and stability, existing approaches rarely consider the reliability of results from different clustering methods, leaving them susceptible to being influenced by the outcomes of poor-performing methods31.

To address these challenges, we propose a novel ensemble learning framework, named SMODEL, for identifying spatial domains from spatial multi-omics data. First, to ensure robust performance across diverse scenarios, we introduce an element-wise weighted ensemble strategy that comprehensively integrates the results from multiple base clustering methods, enhancing the accuracy and robustness of spatial ___domain identification. To reduce excessive reliance on base clustering outcomes, we project multi-omics data with varying features into a shared low-dimensional representation using anchor concept factorization. This approach reduces redundant information caused by noise and adaptively captures the diversity and complementary relationships among different data modalities. Finally, to address the complex manifold structure of spatial data and the nonlinear relationships between cells32,33, we incorporate high-order information between cells and preserve the geometric structure of the original data manifold through graph regularization. This effectively mitigates issues related to spatial smoothing and ensures the integrity of spatial relationships.

We evaluated the robustness and versatility of SMODEL on diverse spatial multi-omics datasets from various platforms, including spatial transcriptomics, proteomics, and epigenomics. Experimental results demonstrate that SMODEL outperforms existing methods in identifying medullary structures within human lymph node datasets. By effectively leveraging complementary information from spatial proteomics and transcriptomics, SMODEL provides deeper insights into the tissue microenvironment, particularly in applications such as breast cancer tissue analysis. In addition, SMODEL enhances the interpretation of spatial gene expression patterns in spatial epigenomic-transcriptomic datasets and effectively integrates spatial triple-omics data while maintaining interpretability. It excels at uncovering consistent and complementary information across different omics. These results highlight the remarkable capability of SMODEL in integrating spatial multi-omics data, revealing cellular heterogeneity, and advancing our understanding of tissue structure and function.

Results

Overview of the SMODEL framework

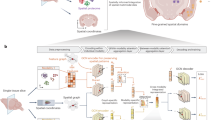
In this study, we developed SMODEL, an ensemble learning algorithm that integrates spatial multi-omics data in a spatially informed manner to analyze cellular heterogeneity. The schematic representation of SMODEL is illustrated in Fig. 1 (detailed descriptions are provided in the “Methods” section). SMODEL is based on the ensemble learning framework, employing the spatial neighborhood structure between cells and the clustering results of various methods as graph constraints, thereby enabling low-dimensional embeddings to effectively preserve positional information as well as base clustering results. The input data for SMODEL comprise the expression matrix of spatial multi-omics data, spatial coordinates, and multiple base clustering results, which are utilized to construct the dual-graph regularized anchor conceptual decomposition integration model. To ensure optimal performance across diverse scenarios, we employed a dual-graph regularization that simultaneously incorporates multiple base clustering results and spatial ___location information. This approach guarantees that the learned spatial consensus representations integrate the strengths of different methodologies while preserving the geometric structure of the original data manifold. Based on the Euclidean distance between any two points in low-dimensional representation, the spatial pseudo-expression (SPE) can be calculated using the 15 nearest neighbors34. SMODEL can be applied to a variety of downstream analysis tasks, which facilitates the elucidation of organizational heterogeneity.

Fig. 1: Schematic overview of SMODEL.
figure 1

SMODEL is a novel dual-graph regularized ensemble learning algorithm designed for integrating spatial multi-omics data. It integrates anchor bases learning, ensemble learning, and spatial consensus representation learning into a unified model. Additionally, SMODEL incorporates high-order information between cells, thereby preserving the local and global similarities of the original data in the low-dimensional manifold. Finally, an element-wise weighting ensemble strategy is employed to integrate multiple base clustering results, achieving optimal performance in multiple scenarios. The output of SMODEL can be readily utilized for various downstream analysis tasks.

Full size image

Benchmarking SMODEL against existing methods on the human lymph node dataset

To evaluate the spatial ___domain identification performance of SMODEL, we applied it on human lymph node datasets that contain spatial transcriptomics and protein expression profiles of two samples. The datasets were generated from 5-μm thick sequential sections of formalin-fixed, paraffin-embedded (FFPE) lymph nodes using the CytAssist Visium platform by 10x Genomics. Ground truth annotations from SpatialGlue27 were employed to assess spatial ___domain identification accuracy and compare SMODEL against seven representative multi-omics methods (Supplementary Note 1).

The manual annotations for human lymph node sample A1 encompassed 10 structural categories, including the pericapsular adipose tissue and capsule as the outer layers, and the cortex and medulla along with their associated sinuses, cords, and vessels as core internal structures (Fig. 2A). The visualization of spatial ___domain identification results across the eight methods for sample A1 (Fig. 2B) highlights the robust performance of SMODEL. The capsule, a fibrous and collagenous membrane enclosing the lymph node, was identified by all algorithms except for scMIC and COSMOS. The cortex, which is critical for immune responses mediated by B cells and T cells, was accurately recognized by SpatialGlue, Seurat, totalVI, PRAGA, and SMODEL, whereas scMIC and MOFA+ failed to detect it. SMODEL effectively discriminated between these spatial domains, thereby enhancing our understanding of their distinct biological roles and spatial organization. Medulla cords are deeply embedded in the innermost region of the medulla of the lymph node, while medulla sinus is a luminal space similar to blood vessels in the medulla, and the two are intertwined with each other in a staggered layout, which makes it difficult to distinguish between them morphologically35. SMODEL effectively distinguished between these spatial domains, thereby enhancing our understanding of their distinct biological roles and spatial organization.

Fig. 2: SMODEL improves the spatial ___domain detection performance on the human lymph node dataset.
figure 2

A Ground truth annotation of human lymph node sample A1. B Spatial plots generated by SpatialGlue, scMIC, totalVI, Seurat, MOFA+, PRAGA, COSMOS, and SMODEL in lymph node sample A1. C Radar chart of the Accuracy, NMI, Purity, F-score, ARI for lymph node sample A1 predicted by SpatialGlue, scMIC, totalVI, Seurat, MOFA+, PRAGA, COSMOS, and SMODEL. D Bar plots displaying ASW values, where a higher value indicates a better spatial ___domain detection accuracy. E Bar plots displaying DBI values, where a lower value indicates a better spatial ___domain detection accuracy.

Full size image

To quantitatively assess the clustering performance, we employed multiple quantitative metrics36. These metrics included five supervised evaluation methods: accuracy (ACC), Normalized Mutual Information (NMI), Purity, F-score, and Adjusted Rand Index (ARI)37. Higher values of these metrics indicate better performance of the method for spatial ___domain identification. In Fig. 2C, we can see that SMODEL outperforms other methods on all the supervised metrics, and its position in the radar graph is closest to the edge, which indicates that it achieves high scores on all these supervised metrics. In addition, we introduced two unsupervised evaluation metrics: the Average Silhouette Width (ASW) and the Davies-Bouldin Index (DBI). ASW evaluates clustering quality by measuring the intra-cluster cohesion of data points and their separation from other clusters38. A higher ASW value indicates a better clustering performance. DBI quantifies the ratio between the tightness and separation of clusters, with lower DBI values implying better clustering39. Figure 2D further demonstrates the superior performance of SMODEL on the ASW metric, with a value of 0.184, which is the highest among all the baseline methods, implying that SMODEL performs the best in maintaining cluster tightness and separation. Meanwhile, SMODEL achieves the lowest DBI value of 1.457 among all baseline methods, further confirming its superiority in spatial ___domain identification (Fig. 2E).

Similar results were obtained by applying the same method to another human lymph node sample D1 (Supplementary Fig. 1-3), indicating the generalization ability and robustness of SMODEL. Overall, these results demonstrate that SMODEL can efficiently identify medullary structures in human lymph node datasets and outperform the existing methods.

Dissecting breast cancer tissue microenvironment using SMODEL

To test whether SMODEL can fully utilize the complementary information provided by spatial proteomics and spatial transcriptomics to deepen the understanding of the tissue microenvironment. We evaluated SMODEL against seven baseline methods (SpatialGlue, scMIC, totalVI, Seurat, MOFA+, PRAGA, and COSMOS) using spatial multi-omics data from mouse breast cancer, comprising 1978 spots, 18,932 genes, and 32 proteins. From Fig. 3A, we can observe that SpatialGlue and PRAGA exhibited strong spatial consistency during clustering but showed considerable noise in boundary transition areas. scMIC displays numerous discontinuous regions and fails to effectively capture the spatial integrity of individual domains. The clustering results of totalVI were spatially more dispersed compared to other methods. The clustering results produced by Seurat exhibit overly uniform cell population distributions at tissue boundaries, failing to accurately capture boundary-specific cellular characteristics. MOFA+ demonstrates good regional continuity in spatial clustering, but struggles with unclear boundaries in transitional areas. The results of COSMOS reveal relatively regular, block-shaped spatial domains. Notably, SMODEL exhibits a significant advantage in terms of clustering performance. Compared to other methods, SMODEL can clearly identify Cluster 1 (purple) and Cluster 2 (green). This suggests that SMODEL can reveal specific features that other methods fail to identify, which may be crucial for understanding the biological properties and functions of cell groups.

Fig. 3: SMODEL can reveal heterogeneity of tissue microenvironment in breast cancer samples.
figure 3

A Spatial plots generated by SpatialGlue, scMIC, totalVI, Seurat, MOFA+, PRAGA, COSMOS, and SMODEL in a tissue section of MMTV-PyMT breast cancer, with each color representing a cluster. B Volcano plot displaying the significantly upregulated and downregulated genes, with the top three markers per cluster highlighted. Upregulated genes are shown in red, while downregulated genes are marked in blue. C Boxplot comparing the average log2 fold change values of SVGs before and after SMODEL denoising. D, E Survival curves of SVGs identified by SMODEL in breast cancer samples obtained from the TCGA database. F Schematic of the macrophage polarization mechanism in breast cancer. Some icons were created by https://biorender.com/.

Full size image

To further investigate the biological significance of the clusters identified by SMODEL, we conducted differential gene expression analysis to identify spatially variable genes (SVGs) within each cluster (Fig. 3B). Using the Wilcoxon rank sum test in combination with the FindAllMarkers function, we identified SVGs with a log2 fold change threshold of 0.25. Further filtering of the marker genes was conducted based on an adjusted p-value threshold of p < 0.05. The volcano plot revealed that Arg1, which encodes arginase 1, was significantly upregulated in cluster 1. The gene expression signature of cluster 1 aligns with the established transcriptional profile of M2 macrophages, which is characterized by high levels of Arg1 expression (Supplementary Fig. 4). The pronounced expression of Arg1 within this cluster not only serves as a molecular marker of M2 macrophage polarization but also underscores its potential as a therapeutic target for modulating the immunosuppressive components of the tumor microenvironment40. Fig. 3A also shows that cluster 1, as M2 macrophages, may establish an immunosuppressive boundary at the tumor edge, which is related to immune depletion and the inability of the body to effectively fight the tumor, which is consistent with the results of previous studies41. The boxplot shows the average log2 fold change in the SVGs for Cluster 2, comparing the data before and after SMODEL denoising. Notable differences are observed between the two conditions. The average log2 fold change after denoising with SMODEL showed improved performance compared with the raw data (Fig. 3C), higher average log2 fold change values suggest that genes are more easily detectable. SMODEL increased the fold change between genes, enabling the identification of additional differential genes that would otherwise remain undetected. This highlights SMODEL’s potential to reveal biomarkers that may be overlooked by other methods. Kaplan-Meier plots for Svopl and Serpini1 showed significant differences in overall survival between high-expression and low-expression groups. Patients with high Svopl expression, identified as an optimistic prognostic biomarker, exhibited better survival outcomes (p < 0.05) (Fig. 3D), whereas high Serpini1 expression, considered a pessimistic prognostic biomarker, correlated with worse survival (p < 0.05) (Fig. 3E). We also performed functional analysis of the SVGs (Supplementary Table 1), which were enriched in pathways closely related to macrophage polarization and cell state transitions.

Additionally, these SVGs are significantly enriched in the JAK/STAT signaling pathway, which is closely associated with macrophage polarization and interactions within the tumor microenvironment. Tumor-associated macrophages, one of the most common immune infiltrating cells in the tumor microenvironment, play a pivotal role in tumor initiation and progression. M0 macrophages can differentiate into the classically activated pro-inflammatory M1 phenotype and the alternatively activated anti-inflammatory M2 phenotype42. M1 macrophages collaborate with Th1 cells and innate lymphoid cells (ILCs) to drive the type 1 immune response. This response mechanism involves the release of cytokines, such as tumor necrosis factor-alpha (TNF-α), activation of cytotoxic T cells to produce reactive oxygen species (ROS), induction of antibody-mediated cytotoxic responses, and direct phagocytosis of tumor cells, demonstrating significant anti-tumor effects43,44,45. After M1 macrophages release anti-inflammatory cytokines in damaged areas, M2 macrophages are attracted to the primary tumor site, where substances produced by type 2 ILCs and Th2 responses, such as interleukin (IL)-10, are present. These substances further trigger a type 2 immune response, activate M2 macrophages, promote the accelerated growth, invasion, and metastasis of tumor cells, increase angiogenesis and lymphangiogenesis, and enhance the immunosuppressive state of the tumor46. Further investigation of the underlying signaling mechanisms showed that the STAT3 pathway plays a critical role in M2 polarization. SMODEL uncovered Lepr as an upstream regulator of the STAT3 pathway, crucial for M2 macrophage polarization (Fig. 3F). Specifically, activation of Lepr leads to the phosphorylation of JAK2, which then phosphorylates and promotes the dimerization of STAT3 protein, activating the STAT3 pathway and boosting cell growth, survival, migration, and invasion. The increase in IL-10 induced by Lepr signaling contributes to the formation of an immunosuppressive microenvironment that facilitates tumor immune evasion. These findings indicate that Lepr could serve as a potential therapeutic target, as inhibiting this signaling pathway may counteract the pro-tumor effects of M2 macrophages and boost anti-tumor immunity.

In conclusion, SMODEL not only shows superior performance in spatial ___domain identification but also offers mechanistic insights into tumor microenvironment heterogeneity. The ability of SMODEL to integrate spatial transcriptomics and spatial proteomics provides a robust framework for the identification of clinically relevant biomarkers. It offers valuable insights into the complexity of the tissue microenvironment and holds significant potential for advancing targeted clinical therapies and improving prognostic assessments.

SMODEL enhances gene expression patterns in spatial epigenome-transcriptome data

We applied SMODEL to the epigenomic-transcriptomic dataset of mouse brains at postnatal day 22, derived from spatial-ATAC-RNA-seq23. This dataset demonstrates a high degree of consistency with anatomical annotations based on Nissl staining, accurately reflecting the regional characteristics of the mouse brain. In this study, we referenced the adult mouse coronal brain anatomical annotations provided by the Allen Brain Atlas47, which primarily encompasses key brain regions such as the cortex (CTX), corpus callosum (CC), lateral ventricle (VL), striatum (Str), anterior commissure (aco), and lateral septal nucleus (LS) (Fig. 4A). To visually compare the performance of the different methods in integrating the mouse brain epigenome-transcriptome dataset, we visualized the results of SpatialGlue, scMIC, MultiVL, Seurat, MOFA+, PRAGA, COSMOS, and SMODEL (Fig. 4B). It was observed that, except for MultiVI, all other baseline methods were able to identify some major regions, such as the core structure (CP) of the striatum in CTX and Str. However, not all methods perfectly corresponded with the anatomical annotations from Allen Brain. In contrast, SpatialGlue and SMODEL could clearly distinguish different layered structures in CTX, which was highly consistent with the anatomical annotations.

Fig. 4: Integration results of SMODEL on samples with spatial epigenome-transcriptome data from the mouse brain dataset.
figure 4

A Anatomically annotated mouse brain images were obtained from the Allen Mouse Brain Atlas. B Spatial plots generated by SpatialGlue, scMIC, MultiVL, Seurat, MOFA+, PRAGA, COSMOS, and SMODEL for the P22 mouse brain sample acquired using spatial-ATAC-RNA-seq, with each color representing a distinct cluster. C Spatial distribution of layer-specific genes in the coronal section of the P22 mouse brain identified using SMODEL, alongside raw data for comparison.

Full size image

The development of the mouse brain is a highly complex and finely regulated biological process that depends on the coordinated expression and precise silencing of numerous genes. During this developmental process, distinct spatial domains are established within the brain, reflecting not only the functional differentiation of brain regions, but also the spatial patterns of gene expression. To further understand and validate the potential of SMODEL in revealing the spatial patterns of gene expression, we analyzed the spatial expression patterns of specific marker genes. SMODEL computed the 15 nearest neighbor cells for each cell based on the spatial consensus representation P, and the average gene expression data of these nearest neighbor cells were used as SPE for that cell. Compared with the raw expression data, SPE significantly enhanced the expression levels of certain layer-specific genes (Fig. 4C). In the Str, we found that the expression level of Pde10a was significantly higher than in other brain regions, and the role of this gene in the striatum is closely related to neuronal signaling and regulation. Pde10a affects neuronal excitability by regulating intracellular cAMP levels48. The CC contains structures such as the genu of the cgenu of corpus callosum (ccg) and the external capsule (ec), serving as the primary connection pathway between the two hemispheres of the brain49. The high expression of Mbp and Tspan2 is closely associated with the myelination process in this region. Mbp plays a crucial role in the stability and function of myelin, while Tspan2 may be involved in intercellular interactions and signaling50,51. The CTX, located in the peripheral area of brain tissue and occupying the largest area, is the center of higher cognitive functions, exhibiting significant organizational layering characteristics52. We found that the expression pattern of Mef2c in CTX was particularly distinct. The VL is a cavity structure filled with cerebrospinal fluid, and the distribution of cell types within its cavity and surrounding areas provides valuable information for studying gene expression in the regions surrounding the ventricles53. Notably, the expression pattern of Dlx1 exhibited clear regional specificity for VL.

Using SMODEL, we significantly enhanced the quality of spatial transcriptomics data by improving marker expression levels, enabling a more accurate representation of expression profiles across different brain regions. In summary, these findings highlight the remarkable ability of SMODEL to effectively integrate spatial epigenomic-transcriptomic data and improve the visualization of spatial expression patterns.

Performance on spatial triple omics integration

Leveraging the anchor concept factorization framework for multi-omics integration, SMODEL is capable of processing not only spatial data from two omics but also extending its functionality to more than three omics. As a case study, we applied SMODEL to integrate spatial triple-omics data simulated using nonnegative spatial factorization decomposition across three omics modalities: RNA, ATAC, and ADT.

Compared to the baseline methods (SpatialGlue, scMIC), SMODEL demonstrates superior performance in matching the ground truth (Fig. 5A). Individual modalities (modality 1, modality 2, and modality 3) exhibited incomplete or noisy patterns. Specifically, the determination of factor 1 was facilitated by the synergistic contributions of modality 1 and modality 3. Factor 2 was identified through a composite analysis involving modality 1, modality 2, and modality 3. Factor 3 was exclusively identified by modality 2, and factor 4 was uniquely identified by modality 3. The imputed modality, derived from the sparse RNA modality, improves the initial patterns, but does not match the accuracy and resolution of other methods. Among the baseline methods, SMODEL is one of the two methods that can accurately identify four factors with minimal noise. The poor performance of scMIC may be attributed to its failure to leverage spatial information, underscoring the importance of spatial information in spatial multi-omics analysis. A radar plot summarizing the evaluation metrics, including NMI, ARI, purity, accuracy, and F-score, showed that SMODEL generally outperformed SpatialGlue, scMIC, and other modalities. Notably, the performance of SMODEL across these metrics highlights its superior clustering and spatial integration capabilities (Fig. 5B). We quantified the contribution of each modality to the final integration results (Fig. 5C). SMODEL assigns weights to each modality, with modality 2 contributing the most (50.5%), followed by modality 3 (30.7%), modality 1 (9.5%), and imputed modality (9.3%). This distribution highlights the ability of SMODEL to effectively prioritize relevant information across modalities. The bar plot illustrates the weights assigned to each modality for different factors (Fig. 5D). Modality 3 maintained a relatively balanced weight across all factors, with a slight increase in factor 5, suggesting that this modality provides complementary information that enhances the accuracy of the integrated dataset. This adaptive weighting mechanism ensures that the integrated results capture the essential spatial patterns embedded in the spatial triple omics data. Moreover, to evaluate noise robustness, we introduced varying levels of sparsity (0.1–0.9) to the non-zero elements of simulated RNA, ADT, and ATAC. As shown in Supplementary Fig. 5, SMODEL demonstrated superior stability characteristics under sparse conditions when compared to other methods.

Fig. 5: Integration of spatial triple omics of simulated data.
figure 5

A Ground truth and spatial plots of modality 1, modality 2, modality 3, imputed modality, SpatialGlue, scMIC, and SMODEL. B Radar plot of clustering performance for different methods. C Pie chart of modality weights. D Bar plots showing the influence of each modality on each cluster, with different colors corresponding to different modalities.

Full size image

Overall, these results highlight the robustness and interpretability of SMODEL in integrating spatial triple-omics data to uncover spatial relationships.

Evaluation of Hyperparameter Selection and Ablation Analysis

To evaluate the impact of hyperparameters on the performance of our method, we conducted sensitivity analyses and ablation experiments. Ablation studies further assess the contributions of individual components, providing insights into the reliability and robustness of the computational model. The 3D hyperparameter landscape (Fig. 6A) reveals significant variations in the NMI score across different values of λ and β, with moderate values indicating a region of stability. Based on a comprehensive analysis of the hyperparameter landscape, it is recommended to set λ to 1 and β to 0.9 for datasets with fewer than 1500 cells. Conversely, for datasets with more than 1500 cells, the default parameters should be adjusted to λ = 10 and β = 0.2. This differentiation is critical to accommodate the increased complexity and variance associated with larger datasets, thereby ensuring that the model maintains its effectiveness and efficiency. Furthermore, the loss curve (Fig. 6B) demonstrates a rapid decline in the objective value during the initial optimization steps, with convergence occurring within 40 iterations. This highlights the efficiency and stability of the SMODEL optimization process. Building on this, an analysis of the NMI performance across varying anchor numbers underscores the impact of anchor selection on clustering accuracy. The results indicate that an anchor number of 100 offers the best trade-off between the accuracy and computational efficiency (Fig. 6C). As the number of anchors increases, the computational time increases substantially, with 200 anchors significantly increasing the time costs compared with 100 anchors (Fig. 6D). This trade-off highlights the importance of selecting an appropriate anchor number to balance performance and efficiency in spatial ___domain reconstruction. Therefore, we recommend a default anchor value of 100. The evaluation of performance metrics across different numbers of neighbors (Fig. 6E) reveals a consistently stable performance, with the best results achieved when using three neighbors. Furthermore, the ablation study (Fig. 6F) highlights the importance of each component within the SMODEL framework, as the complete model consistently outperforms all ablated versions across all metrics.

Fig. 6: Assessment of hyperparameter selection and ablation analysis of the simulated data.
figure 6

A Sensitivity analysis of the hyperparameters. B Objective value variation as a function of iteration steps, showcasing the convergence behavior of SMODEL. C NMI performance for different anchor numbers. D Comparison of time costs for different numbers of anchors. E Performance comparison for different numbers of neighbors. F Radar plot of clustering performance for ablation comparisons.

Full size image

In conclusion, we recommend a default parameter configuration (λ = 10, β = 0.2, anchor = 100, KNN = 12), which is generally suitable for a wide range of data types and applications. Users may further adjust these parameters based on specific requirements to achieve optimal performance.

Discussion

Spatial multi-omics sequencing technology enables the simultaneous analysis of multiple omics data, such as transcriptomics, proteomics, and chromatin accessibility, within individual cells. This approach provides a comprehensive molecular view of tissues while revealing the spatial locations of cells, offering a more complete representation of cellular states. Spatial ___domain identification is a critical step in uncovering cellular heterogeneity from spatial omics data, facilitating a deeper understanding of tissue organization and functional distribution. With the accumulation of spatial multi-omics data, integrating various types of omics data for spatial ___domain identification has become essential for systematically elucidating the molecular mechanisms underlying cellular heterogeneity. However, developing a universally optimal method for spatial ___domain identification remains challenging due to the diverse distributions of data, which can significantly affect model performance across different scenarios.

In this study, we introduce SMODEL, an ensemble learning framework designed to integrate spatial multi-omics data for spatial ___domain identification. Through extensive analysis on five spatial multi-omics datasets, including real and simulated data across different techniques, tissues, and species, we demonstrate the effectiveness of SMODEL in identifying spatial domains. The results highlight the robustness and interpretability of SMODEL in capturing complex spatial relationships while fully leveraging the complementary information provided by spatial multi-omics data. This capability enables in-depth analysis of tissue microenvironments and enhances the understanding of spatial gene expression patterns.

Unlike graph neural network models commonly used for analyzing spatial multi-omics data27,28,29,30, SMODEL leverages anchor concept factorization to extract low-dimensional manifold features. This approach emphasizes the semantic relevance between anchor bases and cell cluster centers, enabling projection learning of concepts defined by the association matrix derived from omics expression data with varying adaptive confidence levels. This process yields a unified spatial consensus representation. Furthermore, SMODEL integrates spatial ___location information and spatial ___domain identification results from existing methods, demonstrating exceptional performance across diverse scenarios. Specifically designed for spatial multi-omics data, SMODEL incorporates preprocessing techniques tailored to the unique characteristics of spatial multi-omics data and is extensible for analyzing additional omics types in practical applications. Its key advantages include modularity, interpretability, robustness, and flexibility, making it a powerful tool for spatial multi-omics data analysis. While SMODEL demonstrates superior performance in terms of accuracy and robustness, we acknowledge that its iterative optimization framework introduces additional computational cost compared to some deep learning-based methods. Spatial ___domain identification is typically performed as an offline analysis task, where the primary objective is to achieve high accuracy in delineating biologically meaningful domains. Given its non-real-time nature, improving the accuracy of ___domain identification has been our main focus. However, improving computational efficiency remains an important direction for future research.

The rapid advancement of spatial multi-omics technologies has enabled the acquisition of multi-dimensional data, offering diverse and complementary views of the same cell at an unprecedented resolution and scale. We plan to extend SMODEL to integrate additional types of omics data, thereby enabling more comprehensive biological insights and improving its scalability to large-scale and high-resolution datasets. Building on this foundation, we will incorporate image data generated by spatial sequencing technologies, particularly hematoxylin and eosin (H&E) staining images, to integrate spatial multi-omics data from a high-resolution perspective. Additionally, we will develop algorithms for integrating spatial multi-omics data across continuous tissue sections, thereby improving the efficiency of spatial ___domain identification and enhancing the potential to uncover cellular heterogeneity.

Methods

Data preprocessing

Spatial multi-omics datasets were downloaded from the Gene Expression Omnibus (GEO) Data Center (https://www.ncbi.nlm.nih.gov/geo/). The data were preprocessed using the SCANPY package54. For all datasets, cells outside the primary tissue region were removed. For the spatial transcriptome, raw expression data were filtered and log-transformed based on library size. Only the top 3000 genes were retained for downstream analysis based on the differences in gene expression. For the spatial epigenome, latent semantic indexing (LSI) dimensionality reduction was performed. Spatial proteomes were preprocessed by normalization and scaling. The expression matrix of different omics is denoted by \({X}^{(v)}\in {{\mathbb{R}}}^{{P}_{v}\times n}(v=1,2,\cdots V)\), the spatial position coordinates are denoted by \(Y\in {{\mathbb{R}}}^{n\times 2}\). Detailed descriptions of each dataset are provided in Supplementary Note 2 and Supplementary Table 2.

The sparse omics imputation

Due to technical limitations, most spatial transcriptomics technologies still result in incomplete expression measurements and a high number of missing values. To address these issues, imputation methods are essential for filling in missing data, thereby improving the overall interpretability of the data. The expression of gene j within cell i can be estimated through a process that considers both the spatial proximity to neighboring cells and the expression similarity to nearby genes. Specifically, the imputed expression value \({X}_{ij}^{c}\) is calculated using the spatial similarity between cells based on Euclidean distance, effectively reflecting the spatial relationships among cells:

$${X}_{ij}^{c}=\left\{\begin{array}{ll}\frac{1}{Q}\mathop{\sum }\limits_{d=1}^{p}{\beta }_{d}{X}_{id} &{{\rm{if}}}\,{X}_{ij}=0\\ {X}_{ij} \hfill &{{\rm{otherwise}}}\end{array}\right.$$
(1)

Here, the weight βj is determined by the decay factor ρ, which ranges from 0 to 1 with a default value of 0.5, and the cell spatial similarity Gc based on Euclidean distance:

$${\beta }_{j}={\rho }^{j-1}\times {G}^{c}({X}_{ij},{X}_{id})$$
(2)

and Q normalization terms:

$$Q=\mathop{\sum }\limits_{d=1}^{p}{G}^{c}({X}_{ij},{X}_{id})$$
(3)

In addition to spatial similarity, gene expression similarity is also considered. \({X}_{ij}^{g}\) is the imputed expression value based on the cosine similarity Gg between genes, which accounts for the genetic relationships that may not be captured by spatial proximity alone.

Finally, the imputed value for gene j in cell i is selected as the maximum of the cell-based imputation \({X}_{ij}^{c}\) and the gene-based imputation \({X}_{ij}^{g}\), ensuring that the most reliable estimate is used:

$${\widehat{X}}_{ij}=\max ({{X}_{ij}^{c}},{X}_{ij}^{g})$$
(4)

Anchor concept factorization

Spatial multi-omics data offer a comprehensive view of individual cells, revealing their intricate biological processes from multiple perspectives. To extract the intrinsic consistency within these spatial multi-omics datasets and obtain a more accurate spatial consensus representation for cell heterogeneity analysis, we introduce an anchor concept factorization55:

$$\begin{array}{ll}\mathop{\min }\limits_{\begin{array}{c}{A}^{(v)},{W}^{(v)},P,{\alpha }_{v}\end{array}} &\mathop{\sum }\limits_{v=1}^{V}{\alpha }_{v}\parallel {X}^{(v)}-{A}^{(v)}{W}^{(v)}P{\parallel }_{F}^{2}\\ \,{\mbox{s.t.}}\, &{A}^{{(v)}^{T}}{A}^{(v)}={I}_{m}\hfill\end{array}$$
(5)

where αv can adaptively learn the corresponding weights from the spatial multi-omics data56. ∥ ⋅ ∥F is the Frobenius norm. \({A}^{(v)}\in {{\mathbb{R}}}^{{P}_{v}\times m}\) is the anchor base of a specific omic, on which orthogonality constraints are applied to make different omics anchor bases independent from each other and more discriminative. Anchors are strategically chosen as the cluster centroids derived from the original data space through the execution of the k-means algorithm, ensuring that they encapsulate the inherent structure of the data. \({W}^{(v)}\in {{\mathbb{R}}}^{m\times k}\) denotes the association matrix with conceptually related anchor bases, a connector between spatial multi-omics data, anchor bases, and spatial consensus representation that collects interaction information and correctly indicates semantic cues. \(P\in {{\mathbb{R}}}^{k\times n}\) is the spatial consensus representation matrix of cells, recording cell expression to the conceptual projections defined by W(v). The anchor concept factorization represents each individual concept as a linear combination of cells, which in turn allows each cell to be expressed as a linear combination of concepts57. Due to the clear semantics of the linear coefficients, it is straightforward to learn the consensus information of the same cell across multi-omics datasets. According to equation (5), this framework can simultaneously investigate three key components: a high-quality set of anchor bases, a set of coefficient representations that elucidate the correlations between these anchors and the underlying concepts, and a spatial consensus representation that integrates the diverse contributions of spatial multi-omics data. It is important to note that these components are not operating in isolation; rather, they are interwoven in a way that fosters a synergistic interaction. This interplay is crucial as it allows the framework to leverage the collective strength of each component, enhancing the overall analytical power and providing a more comprehensive understanding of the complex biological systems under study.

Element-wise weighted ensemble strategy

In order to utilize the different clustering results obtained from the currently available models, we introduce an ensemble learning strategy, and denote the result of the d-th base clustering as B = {π1, ⋯  , πd}, with clsd(xi) denoting the category that the i-th cell belongs to in the d-th cluster, and construct the initial ensemble matrix Ed of the d-th base clustering as:

$${E}_{ij}^{d}=\left\{\begin{array}{ll}1,&cl{s}_{d}({x}_{i})=cl{s}_{d}({x}_{j})\\ 0, &\!\!\!\!cl{s}_{d}({x}_{i})\,\ne\, cl{s}_{d}({x}_{j})\end{array}\right.$$
(6)

The ensemble matrix E0 is constructed by averaging over Ed:

$${E}_{0}=\frac{1}{D}\mathop{\sum }\limits_{d=1}^{D}{E}^{d}$$
(7)

Considering the remarkable diversity among cells, we have found that different basic clustering methods perform unevenly when dealing with different types of cells. Some methods may outperform on some types of cells, but not as well on others. In order to more fully exploit the advantages of each base clusterings, we decided to weight the base clusterings element by element at the cell level. We construct the set of τ nearest neighbors of cell i for the ensemble matrix E0 as follows:

$${\tau }_{i}=\{{x}_{{i}_{1}},\cdots \,,{x}_{{i}_{\tau }}\}$$
(8)

where i1, ⋯  , iτ are the column numbers corresponding to the largest τ elements in the i-th row of E0.

A high similarity between the set of τ-nearest neighbors of a cell and the cluster to which the cell belongs may imply that the algorithm used is able to accurately identify similarities and differences between cells, thus effectively grouping similar cells together. This similarity may reflect cellular interactions, common biological processes, or similar microenvironments. We use the Jaccard coefficient to obtain the correlation weight matrix wid to analyze the similarity between the τ-neighborhood sets and clusters of cells, which helps to gain a deeper understanding of the biological properties and functions of cells.

$${w}_{id}=\frac{| {\tau }_{i}\cap cl{s}_{d}({x}_{i})| }{| {\tau }_{i}| +| cl{s}_{d}({x}_{i})| -| {\tau }_{i}\cap cl{s}_{d}({x}_{i})| }$$
(9)

where \(\left\vert \cdot \right\vert\) represents the number of elements in the set. The better the d-th base clustering is for the i-th cell, the larger the wid. The element-weighted ensemble graph E is calculated as:

$$E=\mathop{\sum }\limits_{d=1}^{D}{({w}_{d}{w}_{d}^{T})}^{\frac{1}{2}}\odot {E}^{d},$$
(10)

where ⊙ represents the matrix dot product. To achieve a stable representation of E, we iteratively update the weighted matrix Wd = {w1, w2, ⋯  , wD}. This process involves following the procedures outlined in equation (8) through equation (9), which guide the generation of the updated weight matrix and its corresponding values. The iterative updating continues until the condition μ < 10−3, where:

$$\mu =\frac{\parallel {E}_{i+1}-{E}_{i}{\parallel }_{F}}{\parallel {E}_{i}{\parallel }_{F}}$$
(11)

The element-wise weighted ensemble strategy in SMODEL is inherently flexible and modular, allowing users to select and combine base clustering methods based on dataset characteristics and specific analytical objectives. There are no strict requirements on which methods must be used, as long as they generate valid clustering results that can be incorporated into the ensemble graph (Supplementary Note 3). Notably, SMODEL does not depend on any single base method. Instead, it leverages the diversity and complementarity of multiple methods, with the ensemble mechanism effectively integrating their strengths while compensating for individual method limitations.

Construction of spatial ___location graph

Valuable insights into high-dimensional data can be derived by analyzing samples embedded within lower-dimensional manifolds. Consequently, it is essential to thoroughly consider the geometric structure of the data within these manifolds. The Euclidean distance effectively captures the spatial relationships among data points and is less influenced by outliers. We use the Euclidean distance to compute the similarity matrix K of cell i at spatial ___location coordinates (Yix, Yiy).

$${K}_{ij}=\sqrt{{\left({Y}_{ix}-{Y}_{jx}\right)}^{2}+{\left({Y}_{iy}-{Y}_{jy}\right)}^{2}},$$
(12)

In manifold learning and spectral graph theory, local invariance is simulated by discretizing the near-neighbor selection of data points to efficiently capture local geometries. Employing the p-nearest neighbor graph(p-NNG) approach58 to get similar cells close enough in cell space to obtain the cell space network G. This approach ensures that similar cells remain proximate, thereby preserving the intrinsic structural information of the dataset.

$${N}_{ij}=\left\{\begin{array}{ll}1,\quad &\,{{\mbox{if}}}\,i\in {N}^{p}\left(j\right)\,{{\mbox{and}}}\,j\in {N}^{p}(i)\\ 0,\quad &\!\!{{\mbox{if}}}\,i\,\notin\, {N}^{p}\left(j\right)\,{{\mbox{and}}}\,j\,\notin\, {N}^{p}(i)\\ 0.5,\quad &\,{{\mbox{otherwise}}}\hfill\end{array}\right.$$
(13)
$${G}_{ij}={N}_{ij}\times {K}_{ij}$$
(14)

where Np(i) and Np(j) denote the sets of p nearest cells to cell i and cell j, respectively.

In order to explore the global information between cells on the basis of local information, we constructed a global co-correlation matrix to describe the higher-order similarity between cells. In the real world, if two people have a lot of common friends, it is very likely that these two people are acquaintances. Inspired by this phenomenon, We use the Pointwise Mutual Information (PMI) matrix59 to capture the high-order topological structure M among cells in the network G, Specifically, the element mij of M is defined as follows:

$${m}_{ij}=log\frac{{G}_{ij}{\sum}_{l}{d}_{l}}{{d}_{i}{d}_{j}}-log\kappa$$
(15)

where Gij represent the weight between the i-th and j-th cells in the cell spatial network G. dl denote the degree of the l-th cell in the network (i.e., the number of edges connected to it). di and dj are the degrees of the i-th and j-th cells, respectively. The parameter κ is typically set to 1 by default. The construction of the PMI matrix is based on the statistical analysis of co-expression patterns among cells, which allows us to identify cell pairs that influence each other not just directly, but through a series of intermediate steps. M as a higher-order topology of the network G enhances the representation of similar relationships between cells. This provides a more accurate characterization of the topology of the network.

Dual-graph regularization

To achieve optimal results across multiple scenarios, we construct an element-weighted ensemble graph E which integrates clustering results from multiple methods, and a higher-order network graph M which captures the high-order relationships in spatial multi-omics data. These two graphs jointly guide the learning of the spatial consensus representation P. A dual-graph regularization term is added to the initial objective function to obtain the final objective function:

$$\begin{array}{l}\mathop{\min }\limits_{{A}^{(v)},{W}^{(v)},P,{\alpha }_{v}}\mathop{\sum }\limits_{v=1}^{V}{\alpha }_{v}\parallel {X}^{(v)}-{A}^{(v)}{W}^{(v)}P{\parallel }_{F}^{2}\\ \,+\,\lambda \,{{\mbox{Tr}}}\,(P(\upbeta {L}_{E}+(1-\beta ){L}_{M}){P}^{T})\\ {{\rm{s.t.}}}\,{A}^{{(v)}^{T}}{A}^{(v)}={I}_{m}\end{array}$$
(16)

where LE and LM are the graph Laplacian matrices of E and M, respectively. For example, LE = DE − WE, where DE is the degree matrix and WE is the adjacency matrix. These Laplacian matrices serve to preserve the local geometry of each graph structure in the spatial consensus representation P by penalizing large variations between connected nodes, thereby enforcing local smoothness and structural coherence. The parameters λ and β are hyperparameters that control the strength of the regularization and the balance between the two graph structures, with values ranging between 0 and 1. This problem can be addressed using an alternating optimization algorithm, which iteratively optimizes each variable while keeping the others fixed. After learning the final spatial consensus representation P, k-means is applied to identify specific cell types, thereby facilitating a deeper understanding of the functional relationships and heterogeneity within tissue regions.

SMODEL optimization

We employed an alternate minimizing algorithm strategy to address the problem in equation (16) mentioned above. Specifically, we decomposed the entire objective function into several subproblems and optimized one variable individually, while keeping the other variables fixed.

A(v)-subproblem: To isolate the impact of A(v) on the objective function, we fixed all other variables at a constant level. Under these controlled conditions, the objective function can be reformulated in terms of A(v) alone as:

$$\begin{array}{l}\mathop{\min }\limits_{{A}^{(v)}}\mathop{\sum }\limits_{v=1}^{V}{\alpha }_{v}\parallel {X}^{(v)}-{A}^{(v)}{W}^{(v)}P{\parallel }_{F}^{2},\\ {{\rm{s.t.}}}\quad {A}^{{(v)}^{T}}{A}^{(v)}={I}_{m}.\hfill\end{array}$$
(17)

Given that each individual A(v) is independent with respect to different spatial omics, the equation (17) can be reconstructed as:

$$\mathop{\max }\limits_{{A}^{(v)}}\,{{\mbox{Tr}}}\,({A}^{(v)T}{B}^{(v)}),\quad {{\rm{s.t.}}}\quad {A}^{(v)T}{A}^{(v)}={I}_{m}$$
(18)

where B(v) is defined as \({B}^{(v)}={X}^{(v)}{P}^{T}{W}^{(v)T}={X}^{(v)}{[{W}^{(v)}P]}^{T}\). By employing the Singular Value Decomposition (SVD) method60, B(v) is expressed as \({U}_{B}{\Sigma }_{B}{V}_{B}^{T}\). Consequently, A(v) is then computed as follows:

$${A}^{(v)}={U}_{B}^{(v)}{V}_{B}^{(v)T}$$
(19)

W(v)-subproblem: By maintaining the other variables constant, W(v) can be updated through the solution of the following problem:

$$\mathop{\min }\limits_{{W}^{(v)}}\mathop{\sum }\limits_{v=1}^{V}{a}_{v}\parallel {X}^{(v)}-{A}^{(v)}{W}^{(v)}P{\parallel }_{F}^{2}$$
(20)

Similarly, the optimization problem with respect to each independent W(v) can be reformulated to:

$$\mathop{\min }\limits_{W(v)}\,{{\mbox{Tr}}}({P}^{T}{W}^{(v)T}{W}^{(v)}P)-2{{\mbox{Tr}}}\,({P}^{T}{W}^{(v)T}{A}^{(v)T}{X}^{(v)})$$
(21)

By taking the derivative of equation (21) with respect to W(v) and setting it to zero61,62, we derive the subsequent update rule for W(v):

$${W}^{(v)}=\left({A}^{{(v)}^{T}}{X}^{(v)}{P}^{T}\right){\left(P{P}^{T}\right)}^{-1}$$
(22)

P-subproblem: By maintaining the other variables constant, P can be updated through the solution of the following optimization problem:

$$\mathop{\min }\limits_{P}\mathop{\sum }\limits_{v=1}^{V}{\alpha }_{v}\parallel {X}^{(v)}-{A}^{(v)}{W}^{(v)}P{\parallel }_{F}^{2}+\lambda \,{{\mbox{Tr}}}\,(P(\upbeta {L}_{E}+(1-\upbeta ){L}_{M}){P}^{T})$$
(23)

To obtain the update rule for P, we calculate the derivative of equation (23) with respect to P and equate it to zero. The detailed derivation is presented in the Supplementary Note 4, resulting in the following:

$$\mathop{\sum }\limits_{v=1}^{V}{\alpha }_{v}{W}^{(v)T}{A}^{(v)T}{A}^{(v)}{W}^{(v)}P\, +P\lambda [\beta {L}_{E}+(1-\beta ){L}_{M}] \\ =\mathop{\sum }\limits_{v=1}^{V}{\alpha }_{v}{W}^{(v)T}{A}^{(v)T}{X}^{(v)}$$
(24)

Equation (24) can be rewritten in the standard form of the Sylvester equation as follows:

$$XP+PY=Z$$
(25)

where

$$\begin{array}{rcl}X&=&\mathop{\sum }\limits_{v=1}^{V}{\alpha }_{v}{W}^{(v)T}{A}^{(v)T}{A}^{(v)}{W}^{(v)}\\ Y&=&\lambda [\beta {L}_{E}+(1-\beta ){L}_{M}]\hfill\\ Z&=&\mathop{\sum }\limits_{v=1}^{V}{\alpha }_{v}{W}^{(v)T}{A}^{(v)T}{X}^{(v)}\hfill\end{array}$$
(26)

When there are no shared eigenvalues between X and Y, equation (26) has a unique solution63. Thus, the update for P can be expressed as:

$$P=\,{{\mbox{sylvester}}}\,(X,Y,Z)$$
(27)

Here, the sylvester (⋅) function solves the Sylvester equation and returns matrix P as the solution.

αv-subproblem: To quantify and optimize the adaptive confidence level weights αv, we consider the reconstruction error of each omic. Initially, the weights for each omic αv are set to be equal, i.e., \({\alpha }_{v}=\frac{1}{V}\), where V is the total number of omics. With the weights αv fixed, the objective function is optimized by minimizing the weighted reconstruction error for each omic. The weights are updated based on the inverse of the reconstruction error, ensuring that omics with lower reconstruction errors receive higher weights. Specifically, the weights are updated as follows:

$${\alpha }_{v}=\frac{1}{2\parallel {X}^{(v)}-{A}^{(v)}{W}^{(v)}P{\parallel }_{F}}$$
(28)

where ∥ ⋅ ∥F is the Frobenius norm.

According to the nature of the alternating optimization process, the objective function value decreases monotonically with each iteration. This equation (28) implies that if the reconstruction error ∥X(v) − A(v)W(v)P∥F is small, indicating that the v-th omic is reliable and informative, the corresponding weight αv will be large. Conversely, if the reconstruction error is large, suggesting that the v-th omic is less informative or noisy, a smaller weight will be assigned to it56.

Complexity Analysis

Time complexity

The computational complexity of SMODEL consists of three parts, corresponding to the optimization of its key components. The first part is anchor concept factorization. For the v-th omic, computing the reconstruction term A(v)W(v)P involves \({{\mathcal{O}}}({p}_{v}mk+mkn)\) operations. Updating A(v) with orthogonality constraints requires \({{\mathcal{O}}}({p}_{v}{m}^{2})\), updating W(v) costs \({{\mathcal{O}}}({m}^{2}k)\), and updating αv requires \({{\mathcal{O}}}(1)\). The second part is ensemble learning, which involves constructing an ensemble similarity matrix using d base clustering results and deriving a corresponding Laplacian matrix. This step requires \({{\mathcal{O}}}(d{n}^{2})\) operations. The third part is dual-graph regularization. Computing the manifold Laplacian incurs \({{\mathcal{O}}}({n}^{2}k)\) operations, and combining Laplacians as well as solving for the consensus representation P adds another \({{\mathcal{O}}}(k{n}^{2}+{k}^{2}n)\) operations. Therefore, the total time complexity of SMODEL over T iterations is given by:

$${{\mathcal{O}}}\left(T\left(V({p}_{\max }mk+mkn+{p}_{\max }{m}^{2}+{m}^{2}k)+d{n}^{2}+k{n}^{2}\right)\right),$$

where T denotes the number of iterations, pv is the feature dimension of the v-th omic, \({p}_{\max }=\max ({p}_{1},{p}_{2},\ldots ,{p}_{V})\)), m is the number of anchors, k denotes the latent dimensionality of the spatial consensus representation P, and n is the number of cells. Since typically n ≫ pv, m, k, the time complexity is dominated by \({{\mathcal{O}}}(T(d+k){n}^{2})\).

Space complexity

The main memory consumption of SMODEL comes from storing the input omic matrices \({X}^{(v)}\in {{\mathbb{R}}}^{{p}_{v}\times n}\), the anchor matrices \({A}^{(v)}\in {{\mathbb{R}}}^{{p}_{v}\times m}\), the weight matrices \({W}^{(v)}\in {{\mathbb{R}}}^{m\times k}\), and the low-dimensional representation \(P\in {{\mathbb{R}}}^{k\times n}\), contributing a total of \({{\mathcal{O}}}(V{p}_{\max }n+V{p}_{\max }m+Vmk+kn)\) in space. Additional memory is required to store the ensemble similarity matrix E and the Laplacian matrices LE and LM, each of size n × n, contributing an additional \({{\mathcal{O}}}({n}^{2})\) space. Thus, the total space complexity is:

$${{\mathcal{O}}}(V{p}_{\max }n+V{p}_{\max }m+Vmk+kn+{n}^{2}),$$

which is dominated by the O(n2) term when dealing with large-scale datasets where the number of cells n is significantly larger than other dimensions.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.