Impacts of climate change on global agriculture accounting for adaptation

Disruptions of the global food system owing to climate change threaten human well-being^12,13,14 and social stability^10,15, but researchers lack a complete understanding of the magnitude and structure of potential impacts on food systems globally^2,16. It is known that changes to the climate will alter the distribution of weather experienced across the planet¹⁷ and that biophysical processes in agricultural systems will respond^5,7,8. However, the degree to which humans around the world will effectively adapt their agricultural practices in reaction to these changes remains unknown^2,3,8,9. For this reason, existing global projections have been unable to account for the adoption rates and efficacy of producer adaptations^7,8,18 and it remains unresolved whether the compensatory responses of producers are likely to overcome the challenges posed by climate change^4,19.

Here we develop a unified empirical approach to measure the effect of climate change on staple crop production, accounting for the costs, benefits and adoption rates of producer adaptations as they are observed in practice around the world. We study one of the most comprehensive samples of subnational crop yields ever assembled, representing two-thirds of global cropped calorie production, which allows our results to be globally representative. Using high-resolution data from populations across diverse contexts allows us to understand the real-world response of producers to weather events, changes in climate and economic development. We then apply our empirical results to project probabilistic global climate change impacts on yields that account for environmental changes, biophysical processes and the compensatory responses of producers.

Previous analyses using process-based models have provided crucial insights about the potential impacts of climate change on global food systems and have enabled decades of progress in agronomic modelling^7,8,9,18. These models explicitly characterize the biophysical processes that generate yields (for example, root depth, evapotranspiration, light utilization) and are calibrated to precisely managed experimental fields^7,18, thereby providing detailed insight into the agronomic mechanisms by which climatic changes influence yields. However, these models generally assume that producers optimize yields subject to decision rules formed through modeller expert judgement (for example, ‘no adaptation’ or ‘optimal varietal switching’^7,18) in contrast to observing the decisions made by producers on the ground^16,20,21. These decision rules describe what is theoretically possible but might not reflect actual conditions across diverse socioeconomic contexts, which are influenced by financial constraints, market failures and human error, along with other factors (Methods). Furthermore, because global process-based models are parameterized on the basis of data from scientifically managed experimental fields, concerns have been raised about their ability to represent actual producer decisions in diverse and resource-constrained contexts^16,20,21.

To address these challenges, we develop an econometric approach that simultaneously captures the combined impact of biophysical crop responses and producer decision-making. In place of modeller-prescribed adaptation scenarios, our approach empirically recovers the effect of actual adaptations undertaken in response to diverse climatic and economic conditions faced by producers. This reduced-form approach does not attempt the difficult task of identifying and modelling each individual mechanism through which these adaptations occur. Instead, we measure the total impact of adaptive adjustments in response to the climate (for example, changing varietals, altering cultivation windows, adjusting fertilizer) without modelling intermediary processes explicitly (Methods and Supplementary Information, section B). We apply these measurements—which capture the extent, intensity and efficacy of real-world producer adaptations as a function of local climates and economic conditions—in simulations of future crop production under climate change and economic development. The key assumption underlying our approach is that producers facing similar climates, incomes and irrigation infrastructure make similar management decisions, which allows us to estimate the effects of producer decisions, which we do not observe. The weakness of our approach is that, if producers facing similar contexts are not comparable, then our estimates of producer adaptation may be biased (Methods and Supplementary Information, section B).

Previous empirical work has demonstrated how reduced-form econometric approaches can be calibrated to producer behaviour in specific regions^2,5,11,22,23, such as maize producers in the USA⁵. Follow-up work demonstrated that this approach is complementary to, rather than a replacement for, detailed process-based models^{8,9,20,23,24,25}. We build on the literature analysing the variation of weather responses with local climate as an indicator of adaptation^4,19,26,27, making use of the method for capturing the benefits of adaptation in ref. ²⁸ and accounting for adaptation costs based on ref. ²⁹. Our work here represents, to the best of our knowledge, the first global analysis of staple crops that: (1) accounts for observed adaptation behaviour and how it varies globally; (2) uses these results to generate global projections of climate impacts on yields over the twenty-first century; and (3) transforms these projections into an empirically derived ‘damage function’ that links changes in global calorie production to changes in GMST (ΔGMST). The scale and scope of our projections are comparable with global gridded process-based models, such as those underlying the Agricultural Model Intercomparison and Improvement Project (AgMIP)⁷. However, unlike those models, our analysis is based on globally representative data and accounts for the adoption rates and efficacy of adaptive behaviours that producers choose to undertake in practice across diverse environmental and economic contexts (for example, varietal switching and optimization of inputs such as fertilizer or irrigation intensity; see Supplementary Information, section B).

We make four contributions that address key challenges when projecting global impacts of climate change on agriculture. First, we assemble one of the largest datasets of subnational crop production available (Ray et al.³⁰ analyse the only comparable dataset we are aware of, containing “~13,500 political units” and four crops, but have not made their data public), covering 12,658 subnational administrative units from 54 countries for six staple crops spanning diverse local climates and socioeconomic contexts (Fig. 1a–c,e, Supplementary Fig. 1 and Supplementary Table 1). Second, we systematically select from many correlated aspects of weather affecting crop biophysical processes which have been separately studied². In our models of crop biophysical processes, we endeavour to ‘let the data speak’ and select from this broad set of weather variables using cross-validation over our rich panel data, an approach commonly used in machine learning (Supplementary Information, section C, Extended Data Figs. 1a and 2 and Supplementary Fig. 2). Third, we estimate the degree of producer adaptation, which has been widely debated^{2,3,4,5,6,19,22,31}. Following previous research, we use climate summary statistics (such as average temperature, average rainfall; see bars in Fig. 1d,f) to identify similarly adapted subpopulations^{4,5,26,28,29,31,32} (Extended Data Figs. 1b, 3 and 4, Methods and Supplementary Information, section D). However, we select crop-specific measures of climate by means of cross-validation (Extended Data Fig. 1c). Further, we account for both the costs²⁹ and the benefits of local adaptations (Methods and Supplementary Information, section H); failing to account for costs overstates the value of adaptation¹⁹. Fourth, our model allows for differences in resource access (for example, fertilizer, technology, insurance and credit markets or labour markets) to influence patterns of food production (Methods). This is particularly important in projections, as future economic development is likely to alter agricultural practices in ways that could make agriculture more resilient or vulnerable to weather³³.

Region-specific and crop-specific impacts are projected to evolve in the future based on changes to economic conditions (for example, GDP per capita) and climate (for example, average temperature), reflecting economic development and adaptation. a, Fraction of cropped area observed in our subnational administrative data, for example, regions spanning North, Central and South America. b, Example inset regions surrounding Lucas do Rio Verde municipality (black outline) in Mato Grosso state, Brazil. c, Time series of maize yield administrative data from Lucas do Rio Verde. d, Empirically estimated relationship between daily temperature and log maize yields (shaded region: 95% confidence interval) conditional on other factors that include rainfall, climate and access to inputs and technology (Methods). Bars indicate county-specific values for variables used to predict the local, county-level effects of temperature and rainfall (red is average temperature, blue is average precipitation, orange is GDP per capita and green is area equipped for irrigation). Example regions depicted from top to bottom are: Iroquois County, Illinois, USA; La Barca municipality in Jalisco, Mexico; and Lucas do Rio Verde in Mato Grosso, Brazil. e, As in a but for an example region of Asia. f, As in d but for the response of rice to daily temperature in Dongbao district in Hubei, China, the cities of Thanjavur and Tiruchirappalli in Tamil Nadu, India, and Sulawesi Utara, Indonesia. g, Expected exceedance degree days over 30 °C projected for each of 24,378 regions in 2090 in a high-emissions scenario (RCP 8.5). Exceedance degree day projections (and other variables) from each model are combined with econometric results, such as d and f, to project crop-specific climate impacts that account for adaptation.

Full size image

Because our data span climatic zones around the world, we are able to empirically measure how adaptive practices in different climates mediate the influence of environmental conditions (Fig. 1d,f and Extended Data Fig. 1b,c). This ‘reduced-form’ approach does not provide the granular detail contained in process-based models but it does account for the net consequence of nearly all climate-associated adaptive actions available to producers, without requiring that each is explicitly modelled or observed²². For example, our approach accounts for adaptive actions such as selecting a varietal with an earlier harvest date to avoid late-season heat exposure, adjusting typical fertilizer use conditional on socioeconomic conditions and adjusting typical irrigation water use conditional on access to irrigation, along with many other available adaptive measures. Notably, our approach does not account for altering the area planted to a given crop (that is, crop switching, although we do account for this in our valuation of climate impacts) and shifting the planting date outside present growing season windows (although we do account for varietal selections with earlier harvest dates).

Our final global model for each crop is high dimensional, nonlinear and dependent on the underlying economic and climatic characteristics of each ___location—but nonetheless fully interpretable. Each crop model includes several measures of weather that are all interacted with several measures of climate, as well as income and possibly irrigation (Extended Data Fig. 1c). This approach allows yields in a given year and ___location to be computed by (1) weather in that ___location–year, which is an argument to (2) a ___location–year function determined by crop-specific measures of climate, income and irrigation. The resulting models are relatively parsimonious compared with global process-based models^7,8 because the influence of many other factors not explicitly included in the model (for example, soil type and quality) is captured non-parametrically (Methods and Supplementary Information, section B). However, these parsimonious models are skilful. Our model outperforms process-based model benchmarks globally across crops and regionally over 81% of crop–country pairs (Supplementary Information, section F and Extended Data Tables 1 and 2). Furthermore, in a ground-truth exercise, our model reproduces variation in local yields (R² values from 0.63 (cassava) to 0.88 (rice); Extended Data Fig. 5), including over localized regions in our data representing both high and low values of average yields and cropping intensity (Extended Data Fig. 6).

We project climate impacts to yields across 24,378 global administrative regions until the end of the century. Projections include a high-emissions scenario (Representative Concentration Pathway (RCP) 8.5; Figs. 1g and 2) and a moderate-emissions scenario (RCP 4.5; Extended Data Fig. 7), each matched to two socioeconomic scenarios, in each of 33 climate models and model surrogates that represent the full range of climate sensitivities (Methods). We account for statistical uncertainty through 1,920 Monte Carlo simulations per crop, following refs. ^28,29,34 (Methods).

a–f, Colours indicate central estimate in a high-emissions scenario (RCP 8.5), net of adaptation costs and benefits, for maize (a), soybean (b), rice (c), wheat (d), cassava (e) and sorghum (f) for 2089–2098. Projections computed for 24,378 subnational units relative to counterfactual yields, uncropped regions are shaded in grey. Wheat shows winter wheat and spring wheat projections combined, weighted by their area share in each region. Estimates in each ___location are ensemble means across climate and statistical uncertainty. Incomes from SSP3. See Extended Data Fig. 7 for a moderate-emissions scenario (RCP 4.5) and Supplementary Information, section J for results adjusted by CO₂ fertilization.

Full size image

We report results based on where crops are cultivated today, noting that our approach also allows us to estimate theoretical impacts for a crop in locations in which it is not cultivated at present (Supplementary Fig. 7).

The projected effects of climate change on crop yields vary around the world (Fig. 2 and Supplementary Figs. 10 and 11). Regions exhibit different initial climates and socioeconomic conditions and they experience different changes in temperature, precipitation and incomes. These in turn alter the environmental factors crops are exposed to and the adaptive decisions of producers. Our projections are deviations from local baseline yield trends, which have historically been positive^30,35 and will probably remain generally positive (see the ‘Conclusions and discussion’ section).

First, for all crops, temperature changes (through degree days and minimum temperature for rice and wheat) generally dominate the sign of local projected impacts. Precipitation strongly influences inter-annual variability in yields—which is important to producers, consumers and government planners—but does not generally drive overall trends. Global patterns in yield losses reflect the nonlinear response of crops to temperatures, with increasing extreme heat depressing yields and reductions in cold days increasing yields. Adaptive responses to rising average temperature moderate losses to extreme heat (for example, Extended Data Fig. 3a), consistent with producers taking protective measures in response to temperature extremes that are expected¹⁹. However, benefits from these protective measures are partially offset by decreased yield gains during moderate temperatures. The trade-off between temperature resilience and average yield has been documented and is understood to reflect physiological compromises across varietals^19,36, although its potential global impact on future food production has not been previously demonstrated or quantified.

A second general pattern across several crops applies to equatorial regions of the world with high rainfall, including central Africa, Southeast Asia and South America. In these regions, the benefits of moderate temperatures are amplified by increasing levels of precipitation, driven by an intensifying water cycle³⁷. Although rising temperatures may ultimately reduce yields in these regions, the benefits of high rainfall in these regions partially offset those effects.

Maize

Under a high-emissions scenario, our projected end-of-century maize yield losses are severe (about −40%) in the grain belt of the USA, Eastern China, Central Asia, Southern Africa and the Middle East (Fig. 2a, Extended Data Fig. 7a and Supplementary Figs. 10 and 11). Losses in South America and Central Africa are more moderate (about −15%), mitigated in part by high levels of precipitation and increasing long-run precipitation (Extended Data Fig. 3b). Impacts in Europe vary with latitude, from +10% gains in the north to −40% losses along the Mediterranean. Gains in theoretical yield potentials occur in many northern regions in which maize is not widely grown (Supplementary Fig. 7).

Soybean

The spatial distribution of soybean yield impacts is similar in structure to maize, although magnitudes are accentuated (Fig. 2b, Extended Data Fig. 7b and Supplementary Figs. 10 and 11); for example, about −50% in the USA and about +20% in wet regions of Brazil under a high-emissions scenario.

Rice

High-emissions rice yield impacts are mixed in India and Southeast Asia, which lead global rice production, with small gains and losses throughout these regions. This regional result is broadly consistent with earlier work¹. In the remaining rice-growing regions, central estimates are generally negative, with magnitudes in Sub-Saharan Africa, Europe and Central Asia exceeding −50% (Fig. 2c, Extended Data Fig. 7c and Supplementary Figs. 10 and 11).

Wheat

Wheat losses are notably consistent across the main wheat-growing regions, with high-emissions yield losses of −15% to −25% in Eastern Europe, Western Europe, Africa and South America and −30% to −40% in China, Russia, the USA and Canada (Fig. 2d, Extended Data Fig. 7d and Supplementary Figs. 10 and 11). There are notable exceptions to these global patterns: wheat-growing regions of Western China exhibit both gains and losses, whereas wheat-growing regions of Northern India exhibit some of the most severe projected losses across the globe.

Cassava

Cassava is projected to have uniformly negative projected impacts in nearly all regions in which it is grown at present, with the largest losses in Sub-Saharan Africa (−40% on average under a high-emissions scenario). Although cassava does not make up a large portion of global agricultural revenues, it is an important subsistence crop in low-income and middle-income countries. Thus, these yield losses may be a substantial future threat to the nutritional intake of the global poor (Fig. 2e, Extended Data Fig. 7e and Supplementary Figs. 10 and 11).

Sorghum

Sorghum losses are widespread in almost all of the main regions in which it is grown at present: North America (−40%), South Asia (including India) (−10%) and Sub-Saharan Africa (−25%). Projected gains emerge in Western Europe (+28%) and Northern China (+3%) (Fig. 2f, Extended Data Fig. 7f and Supplementary Figs. 10 and 11).

We compute aggregated global yield impacts based on the present distribution of global croplands, accounting for adaptation benefits and costs (Fig. 3a). For all crops except rice, we estimate that warming will likely reduce global yields by 2050 (probability of loss ranges from 0.701 (sorghum) to 0.946 (wheat), high-emissions scenario) after accounting for both statistical and climate model uncertainty. Central estimates for global end-of-century losses under the high-emissions/moderate-emissions scenarios (RCP 8.5/RCP 4.5) are −27.8%/−12.0% (P = 0.258/0.308) for maize, −6.0%/−1.1% (P = 0.477/0.475) for rice, −35.6%/−22.4% (P = 0.185/0.206) for soybean, −29.8%/−12.8% (P = 0.179/0.248) for cassava, −21.7%/−5.9% (P = 0.329/0.417) for sorghum and −28.2%/−13.5% (P = 0.038/0.058) for wheat. End-of-century uncertainty ranges may be substantial, with the largest 90% credible range for rice (q5 = −58.6%; q95 = 109.4%; RCP 8.5) and the narrowest range for wheat (q5 = −20.7%; q95 = −10.4%; RCP 4.5). These ranges allow for moderate likelihood that the impact of high emissions on global yields is positive for rice (probability = 0.477), maize (probability = 0.258), cassava (probability = 0.179) and sorghum (probability = 0.329) or more negative than −30% for rice (probability = 0.240), maize (probability = 0.417), sorghum (probability = 0.410), wheat (probability = 0.535), soybean (probability = 0.560) and cassava (probability = 0.481).

a, Time series of projected climate change impacts on global average yields (area-weighted) in a high-emissions scenario (RCP 8.5), accounting for producer adaptations and adaptation costs. Box and whisker plots show total distribution of end-of-century projections accounting for joint statistical and climate model uncertainty (in each subplot: boxes, 25th to 75th percentiles; whiskers, 5th to 95th percentiles). To the right are projections adjusted for the estimated effect of CO₂ fertilization from ref. ⁹ (shaded) and projections for moderate emissions (RCP 4.5) without CO₂ fertilization (unshaded). See full results for moderate emissions in Supplementary Fig. 8, CO₂ fertilization in Supplementary Information, section J, and uncertainty in Supplementary Figs. 4 (RCP 8.5) and 5 (RCP 4.5). b, Projected end-of-century yield impacts, by deciles of present-day average temperature over 24,378 regions. Impacts across crops weighted within region by cropped area and caloric content; distributions across regions weighted by total cropped area. c, As in b but by decile of present-day income. d, Empirical end-of-century global damage function describing calories (kcal) lost as a quadratic function of global mean surface temperature anomaly (ΔGMST). Each point represents a single climate-model-by-Monte Carlo run for RCP 4.5 (blue) or RCP 8.5 (red) in 2093–2097, including gains from CO₂ fertilization. Grey bands indicate 10th–90th and 25th–75th quantile bands, conditional on ΔGMST. Bottom panel shows the distribution of warming under each RCP across 33 climate models and model surrogates (Supplementary Information, section G). Box plots to the right show distribution of damages collapsed to RCP. Right axis describes calorie losses normalized by 2015 global calorie production for the six crops studied here. Projected log(yield) impacts for panels a–c winsorized at the top and bottom 1% of the impacts distribution over all region–GCM–years, by RCP–crop, then converted to percentages.

Full size image

Impacts by climate

Although the impact of heat on yields is nonlinear and pronounced for many crops (Extended Data Figs. 3 and 4), global aggregate yields are not driven downward most strongly by the hottest regions of the world. Accounting for adaptation, we find that the middle 50% of regions with moderate average temperatures tend to suffer the largest yield losses (Fig. 3b). This is largely because hotter locations are already more adapted to heat, so further warming has a reduced impact, whereas cold locations benefit from warming. Furthermore, high average rainfall, prevalent in many hot locations, is linked to increased gains from moderate warming (Extended Data Figs. 3b and 4b). This finding underscores the importance of accounting for real-world patterns of differentiated adaptation in global-scale analyses.

Impacts by income

Our projections suggest that changes in global yields affect populations around the world unequally. We estimate that total calorie production is generally affected more heavily by climate change in regions that are richer today (Fig. 3c), along with the lowest-income decile owing to its reliance on cassava. We estimate average losses of 28% in the lowest-income decile but more moderated losses of roughly 18% across deciles 2–8. In the highest-income deciles, average losses increase to 29% (ninth) and 41% (top). This result is partially because lower-income populations tend to live in hotter climates, in which present adaptation rates are higher, and in the tropics, in which high average precipitation reduces warming impacts (Fig. 3b). This has important implications for global damages, as high-income regions include many of the world’s breadbaskets. Because relative yield losses are greatest in regions in which modern agriculture is concentrated, they have amplified influence on global caloric production under climate change.

Global calorie production

We combine our projections across all six crops to estimate the total potential impact of warming on global caloric production (Methods and Supplementary Information, sections B and K). Following the approach in refs. ^28,29,34, we index lost calorie production against ΔGMST for each climate model. We recover a damage function describing the joint distribution of ΔGMST and lost calorie production for these six staple crops in each 5-year moving window of the twenty-first century (Fig. 3d). We estimate that the magnitude of impacts to present croplands increases nearly linearly at a rate of −5.54 × 10¹⁴ kcal (P < 0.001, 95% credible interval −5.63 to −5.44 × 10¹⁴ kcal) of calorie production per +1 °C in GMST in 2100 (see Supplementary Fig. 21 for other decades), amounting to approximately −121 kcal per day per 1 °C per person based on Shared Socioeconomic Pathway 3 (SSP3) 2100 global population projections, or −4.4% of present per capita recommended consumption per 1 °C. (For example, warming of 4 °C in GMST in 2100 would correspond to a loss of about 17.6% of present per capita recommended consumption).

The role of adaptation and development

In contrast to previous global analyses^7,8, projections here account for producer adaptation rates that reflect observed behaviour. We find that accounting for climate adaptation, its costs and rising incomes have substantial impact on high-emissions projections for all crops and regions (Table 1). We estimate that development and adaptive adjustments reduce global calorie impacts (relative to a ‘no adaptation’ scenario) by roughly 23% in 2050 (column 1a versus 1b, Table 1, 6% for moderate emissions) and 34% at the end of the century (column 2a versus 2b, 12% for moderate emissions), owing to the growing extent of adjustment under greater climatic change. The relative impact of adaptation is largest for rice (79% reduction of end-of-century impacts, 86% for moderate emissions) and smallest for wheat (statistically unchanged) (Supplementary Tables 10 and 11). Adaptation and development exacerbate average wheat losses from climate change (Supplementary Figs. 4 and 5 and Supplementary Tables 10 and 11) because wheat producers are observed to take on further weather-related risk as GDP per capita rises (Supplementary Information, section G), resulting in small losses from adaptation and development for Europe and Oceania (Table 1). By contrast, the largest regional benefits of adaptation accrue to South America (61% reduction of end-of-century impacts, 23% for moderate emissions), mostly from maize and soybean adaptation gains. Our results indicate that producer adaptations are likely to have strong influence over climate change impacts to agriculture, highlighting the critical importance of accounting for these adaptations; however, our central estimates for the overall impact of climate change on potential production of staples remain negative and meaningful, even accounting for the net effects of adaptation. Substantial uncertainty persists in these estimates, originating from both econometric uncertainty and climate model uncertainty, such that overall risks should be assessed across the full range of projected impacts.

Adjustments for CO₂ fertilization

The above results do not account for CO₂ fertilization, which is challenging to measure empirically. However, we adjust our results post-estimation to incorporate CO₂ fertilization using previous estimates⁹ (Methods and Supplementary Information, section J). Adjusting for CO₂ fertilization does not qualitatively alter the structure of our findings (Supplementary Figs. 13–18) but it does reduce the central estimate for end-of-century yield losses by 5.0– 9.5 percentage points (Fig. 3a) and increases the likelihood of positive aggregate effects. We do not account for the decreased crop nutrient content that might result from CO₂ fertilization³⁸.

Losses to future global yields can be incorporated into present-day climate policy, for example, by computing the net present value of future economic harms that result from the present emission of an extra ton of CO₂, a value known as the social cost of carbon (SCC). We compute a component of the SCC—a ‘partial SCC’—that results from changes in global yields by integrating these projections into the Data-driven Spatial Climate Impact Model (DSCIM) developed in refs. ^28,29 (Methods and Supplementary Information, section K). We assign country-specific average prices to total calorie production (Supplementary Fig. 20), allowing producers to intensify/reduce production to meet demand in their market at increasing marginal cost (Methods, Supplementary Information, section K, and Supplementary Fig. 19). In general, aggregate yield losses under climate change harm consumers as caloric consumption is lower and prices are higher; producers are also harmed by production losses, but these may be offset by gains from higher prices. In all scenarios, our approach implicitly allows the spatial distribution of within-crop varietals to adjust optimally within present cropped locations (Extended Data Fig. 1, Methods and Supplementary Information, section B). In some further scenarios, we deflate these estimates to account for the roles of crop switching and international trade, which might cause the spatial distribution of planting areas to shift (Methods and Supplementary Information, section K).

Across different modelling assumptions, the partial SCC for the crops we study ranges from $0.99 per ton of CO₂ (5% constant discounting; adjusted for flexible crop switching, movement of cropped land and international trade; moderately elastic demand and supply; frictionless trade within countries; RCP 8.5) to $49.48 per ton (Ramsey discounting³⁹; crop type and land distributions mirror present day; moderately elastic demand and supply; frictionless trade within countries; RCP 8.5). See Extended Data Table 3 and Supplementary Table 13 for all partial SCC estimates.

Our analysis of staple crops is, to the best of our knowledge, the first to quantify the adaptations of real-world producers to climate around the world and to apply these measurements to projections of global agricultural damages from climate change. Our econometric results complement a well-developed literature from process-based models that resolve the underlying mechanics of crop production and some important forms of adaptation but which take producer decision rules as exogenous^7,8,18,20. Our results indicate a substantial and statistically significant rate at which ΔGMST reduces the ability of present global food systems to produce calories, net of adaptation. However, in the absence of adaptation, we project that agricultural outcomes would be materially worse.

Our findings indicate that projected consumption losses tend not to be evenly distributed across global populations. Wealthy regions of the world more easily absorb grain price shocks. In poor regions of the world, food shortages and associated price shocks may be more destabilizing. This suggests that future modelling efforts would benefit from representing realistic costs and benefits of adaptation, imperfect information and other aspects of producer decision-making. We expect that these changes would lead to projections of climate impacts to agriculture that are less optimistic than those assuming agronomically optimal management⁷ and more optimistic than models that do not model adaptation at all².

A key finding is that global populations exhibit extensive adaptation to climate already, especially in relatively low income and hot regions of the world—with the exception of the world’s poorest, who depend heavily on cassava and face higher potential losses (Fig. 3b,c, Supplementary Information, section I.3 and Supplementary Fig. 9). We also observe that breadbaskets of the world, in which the climate is moderate, exhibit more limited adaptation at present. Because such a large fraction of agricultural production is concentrated in these wealthy-but-low-adaption regions, they dominate projections of global calorie production, generating much of the global food security risk we document. This result is consistent with earlier regional findings that US crop systems are optimized for high average yields but not robustness to climatic changes³⁶ and that projected maize losses in Sub-Saharan Africa are largest in the most productive and climatically moderate countries, whereas countries with hotter present-day climates have lower historical yields and smaller projected yield losses⁴⁰.

Our projection of productivity declines under climate change contrasts with process-based model results that are calibrated to experimental farms, use researcher-defined adaptation rules and generally tend to indicate productivity gains globally (ref. ⁸ is an important exception). For example, ensemble mean projections of AgMIP process-based models indicate end-of-century productivity gains for maize (+1.3%, RCP 8.5), wheat (+9.9%), soybean (+15.3%) and rice (+23.3%)⁷. These differ substantially from the generally negative impacts we predict, with central end-of-century estimates that range from −35.6% (soybean) to −6.0% (rice) (Supplementary Table 10; RCP 8.5), although both sets of projections exhibit large uncertainties. A comparison of model skill over historical data suggests that the statistical approach of this paper outperforms the AgMIP ensemble across crops and locations (Extended Data Tables 1 and 2 and Supplementary Information, section F) and accurately captures observed variation in local yields (Extended Data Figs. 5 and 6 and Supplementary Information, section F). These differences highlight the importance of using globally representative data and accounting for empirically measured rates of adaptive behaviours in projections of climate change damages. Unlike process-based crop models, our estimates do not provide insight about the agronomic mechanisms through which climatic changes influence future yields. Such insight is useful in guiding agricultural innovation and, indeed, process-based models are used at present in a Genotype by Environment by Management (GxExM) framework to target crop science research about future climate stresses^41,42,43,44. The work we present underscores the urgency and importance of such crop technology developments and the importance of ensuring access to adaptive technologies by global producers broadly.

Future producer adaptation to climate change may differ from the historically observed patterns we recover. For example, technological breakthroughs, such as the industrial fixation of nitrogen, transformed what is understood about the limit of global productivity. However, the repeatability and penetration of these innovations has been uneven and perhaps should be interpreted cautiously—for example, synthetic fertilizers remain incompletely deployed despite their invention long ago⁴⁵ and progress towards heat tolerance for some staple crops has stalled⁴⁶. Furthermore, to the extent that these advances are correlated with income, our projections implicitly account for them. Notably, innovation has contributed positively to average yield trends in many regions^30,35, which will probably continue into the future in some form. Our projected yield impacts should therefore be interpreted as deviations from a future trend in average yields that is driven by other factors, including innovation. Indeed, our findings provide a sense of the scale required of such innovations to maintain global food security.

Finally, our monetization of agricultural damages from climate change is limited, as it does not capture the impact of all future changes, such as linkages between climate change, food availability and social instability^10,15. Nonetheless, synthesizing the complex global response of agriculture into a partial SCC is an important step towards representing these damages in climate policies⁴⁷. Comparison of our partial SCC with existing estimates provides context for these findings. The Framework for Uncertainty, Negotiation and Distribution (FUND) model reports a partial SCC for agriculture of −$2.70 per ton CO₂ (ref. ⁴⁸) using a 3% discount rate (that is, warming improves global welfare through agriculture). Because this value relies on older (pre-2000) studies for calibration⁴⁹, Moore et al.⁹ construct a revised estimate based on a meta-analysis of previous estimates⁸, mostly from process-based models. Inserting these projections into a computable general equilibrium model for 16 regions, Moore et al.⁹ estimate a partial SCC of $13.05 per ton (adjusted to the USD in 2023), opposite in sign from the original FUND partial SCC. Because this estimate is derived from process-based models, it does not account for observed rates of producer-level adaptation and it is two to five times larger than the range of our comparable estimates, $3.08–$6.84 (3% discount rate; Extended Data Table 3), that do account for autonomous adaptation. We note that, in a recent paper⁵⁰, researchers incorporate the Moore et al.⁹ results directly into the Greenhouse Gas Impact Value Estimator (GIVE) integrated assessment model and find that climate damages to the agricultural sector increase to $84. The discussion of that paper focuses on other aspects of the analysis and does not detail why this estimate changed. Also, neither Moore et al.⁹ nor this study account for non-staple crops or livestock, an important area for future work, and neither estimate accounts for the unequal impact of crop losses on the global poor (Fig. 3c), for whom lost agricultural revenues and/or consumption may be particularly damaging^10,14,15. In continuing work⁵¹, we seek to more fairly represent these unequal costs in global estimates of monetized damages.

This section provides an overview of the data and methods used to estimate the relation between agricultural yields and variation in weather, accounting for adaptation to climate and economic development.

Agricultural data

Subnational yields, production and harvested area, primarily at the second administrative level, were collected from the statistical offices of 54 countries (Supplementary Fig. 1 and Supplementary Table 1). This includes data that were generously shared for Burma, Cambodia, Laos, Malaysia, Thailand⁵² and Zambia⁵³. This yields a dataset for 6 crops in 12,658 locations (41,186 ___location–crop pairs) spanning up to 137 years. Wheat varietals, when not identified in the data, were manually assigned to spring or winter wheat based on ancillary country-specific data (Supplementary Table 6). All growing season definitions are from ref. ⁵⁴ and held fixed. Detailed information is provided in Supplementary Information, section A.

Historical weather data

The main weather dataset used in this analysis is the Global Meteorological Forcing Dataset (GMFD v1)⁵⁵. Data are available on a 0.25° × 0.25°-resolution grid from 1948 to 2010. We obtain daily maximum and minimum temperatures and daily total precipitation for all grid cells globally. These data provide surface temperature and precipitation information using a combination of observations and reanalysis, which is downscaled and bias-corrected using several station-based observational datasets to remove biases in monthly temperature and precipitation.

Projected weather data

We use the NASA Earth Exchange (NEX) Global Daily Downscaled Projections (GDDP) dataset for future projections of climate change. This comprises 21 climate projections, which are downscaled to 0.25° × 0.25° resolution⁵⁶ from global climate model (GCM) runs in the Coupled Model Intercomparison Project Phase 5 (CMIP5) archive⁵⁷. NEX-GDDP uses GMFD⁵⁵ and quantile mapping to adjust the GCM outputs (means and variances) in historical and future time periods so that the systemic bias of the GCMs is removed. In contrast to other approaches⁵⁸, NEX-GDDP does not assume a common distribution shape between observed (GMFD) and GCM data. However, NEX-GDDP only assumes that GMFD (versus GCM) variances are correct, which other approaches⁵⁸ do not require. Climate is projected under emissions from Representative Concentration Pathways 4.5 and 8.5 (RCP 4.5 and RCP 8.5) up to 2100 (refs. ^59,60), although the NEX-GDDP outputs of some models lack precipitation data past 2098, so that the ‘end of the century’ in this paper is the year 2098. The CMIP5 ensemble of GCMs is not a systematic sample of possible futures. To provide an ensemble of climate projections with a probability distribution of GMSTs consistent with that estimated by a probabilistic simple climate model, we use the method outlined in ref. ⁶¹ to assign probabilistic weights to climate projections. A full list of models and their weights is given in Supplementary Table 9. For a more complete description, see ref. ²⁹.

Historical income data

We obtain national and subnational income data for 1,503 administrative regions from 83 countries from ref. ⁶². Data are provided by ref. ⁶² at the state/province level for each country. We use these subnational data to allocate national GDP data from the Penn World Tables (PWT) database (https://www.rug.nl/ggdc/productivity/pwt/) under the assumption that the within-country distributions of GDP recorded in ref. ⁶² are accurate, but the exact levels may not be. Using these data, we construct a consistent panel of subnational incomes for all areas in our crop dataset that sum to the national GDP from the PWT database for all countries in the sample.

Projected income data

Future projections of national incomes are derived from the Organization for Economic Co-operation and Development (OECD) ENV-Growth model⁶³ and the International Institute for Applied Systems Analysis (IIASA) GDP model⁶⁴, as part of the ‘socioeconomic conditions’ of the Shared Socioeconomic Pathways (SSPs)⁶⁵. These are the only models that provide GDP per capita projections for a wide range of countries in the SSP database. The SSPs propose a set of plausible scenarios of socioeconomic development over the twenty-first century in the absence of climate impacts and policy. Data are interpolated to annual frequency and downscaled following ref. ²⁹.

Irrigation data

We obtain data on the area equipped for irrigation from AQUASTAT of the Food and Agriculture Organization of the United Nations (FAO)⁶⁶. These data are a single cross-section centred around the year 2000 at 0.08° × 0.08° resolution and we hold the values fixed in climate projections. (Increases in incomes and heat exposure may drive increases in future irrigation, whereas aquifer and reservoir drawdown may drive decreases in future irrigation).

Model overview

We develop a reduced-form approach to modelling crop yields and producer adaptation, allowing us to recover plausibly causal effects of weather on yields based on data from real-world farms, without having to observe all of the biophysical processes in a given crop that mediate these effects. The approach allows us to account for the total costs and benefits of numerous real-world adaptive adjustments that producers undertake, without requiring that we observe or model each adjustment explicitly. This approach builds on ideas and techniques developed in refs. ^4,19,26,27, using the method for capturing the benefits of adaptation in ref. ²⁸ and accounting for its costs based on the revealed preference approach in ref. ²⁹. Following common practice in the literature², our implementation also allows our model to recover local, micro level and instantaneous nonlinear effects of environmental conditions, even though outcome data are only observed at more aggregate spatial scales and temporal frequencies^28,31.

We apply cross-validation techniques common in machine learning but adapted for model selection in a causal inference context. Our approach has three stages: (1) we remove variation that is associated with non-parametric controls to condition out the influence of unobservables; (2) we apply cross-validation to this residualized data to select weather measures; and (3) we again apply cross-validation, modifying the model chosen in the previous step to select dimensions of climate that matter for adaptation. We perform the sequence (1)–(3) for each of the six crops separately to identify the most suitable model for each crop. Having selected and fitted an empirical model that accounts for weather and adaptation, we then apply the model in projections of climate change impacts. Each of these steps is detailed below.

Construction of weather terms

A large number of candidate weather variables are constructed from raw weather data based on previous literature^{5,67,68,69,70,71}. We assemble variables that previous analyses report were influential for at least one crop, although individual variables might not ultimately be included in the specification for all or any crops. All weather transformations were conducted at the pixel level using daily data before aggregation, unless otherwise specified. Encoding pixel-by-day weather data after nonlinear transformations allows a high degree of flexibility in how local daily weather conditions can have an instantaneous and nonlinear impact on crops^28,31. This means that even short periods of environmental stress are resolved and captured by these variables and the model. Degree day terms were constructed following ref. ⁵, with kink points selected for each crop by a tenfold cross-validation search over potential kinks. Growing-season-phase precipitation was summed within month by grid cell and then transformed⁷⁰. Construction of vapour pressure deficit followed ref. ⁶⁹. The count of rain days was calculated by grid cell as days with positive precipitation⁶⁸. Extreme rain was identified by constructing the 1980–2010 rainfall distribution for each grid cell in the GMFD daily precipitation data and aggregating the amount of rainfall or number of days of rainfall in excess of the 95th percentile of this distribution⁶⁸. Count of extreme rain days was measured following extreme rain except grid cell days were counted instead of summed within grid cell⁶⁸. Drought was defined as a binary indicator over administrative unit growing season precipitation, using a tenfold cross-validation search over percentile cut-offs in the administrative unit growing season total precipitation distribution, largely following ref. ⁷¹ (final cut-offs ranged from the 8th to 25th percentiles). Minimum temperatures were calculated as the average of daily grid cell minimum temperatures within each month, following ref. ⁶⁷. For all weather terms, weighting and aggregation to administrative units were done as described in ref. ²⁹ with cropped area weights from ref. ⁵⁴. See Supplementary Information, section D and Supplementary Tables 2–5 for full details on the construction of each weather variable.

Cross-validation step zero: residualizing data for causal inference

We first select non-parametric controls for unobservable factors to isolate plausibly random variation in our set of weather measures^5,22,31. Specifically, we use administrative unit i (typically county), fixed effects \({\mu }_{i}\), absorbing time-invariant confounds such as soil quality; country–year fixed effects \({\rho }_{ct}\), absorbing country-by-year price and trade policy confounds; and state or province quadratic time trends \({h}_{s}(t)\), absorbing slow-moving, local confounds such as the diffusion of new technologies or local variation in prices (equation (1), Supplementary equations (B.12) and (D.1)–(D.6)). We separately partial out the variation in yields y_it and the vector of regressors x_it on these non-parametric controls (Supplementary Information, section B), leaving us with residual variation \({\widetilde{y}}_{it}\) and \({\widetilde{{\bf{x}}}}_{it}\) for our cross-validation procedures.

Cross-validation step one: selection of weather measures

We implement cross-validation over ten random folds to systematically evaluate the importance for yields of the broad range of weather measures previously described in the literature. Each potential model is required to have at least one temperature term and one moisture term. (Temperature and precipitation are known to be correlated, so causal effects estimation of one without controlling for the other is vulnerable to bias⁵. Vapour pressure deficit was treated as a moisture term. Note: these terms may affect moisture demand and/or soil moisture supply). Weather terms are each interacted with a fixed set of covariates: growing season average daily maximum temperature (‘long-run temperature’, \(\overline{T}\)), growing season average monthly precipitation (‘long-run precipitation’, \(\bar{P}\)), log(GDP_pc) (‘income’, \(\bar{I}\)) and the share of cropped area equipped for irrigation (‘irrigation’, \(R\)). This ensures that weather variable selection occurs using models that are at least as flexible as those selected after the second cross-validation step, without having to simultaneously explore the full set of potential combinations of weather measures and covariate interactions (which would number 103,904 separate models). In selecting a candidate set of weather terms over which to study adaptation, we seek to optimize over parsimony and explanatory power, selecting a high-performing model in which additional weather terms do not individually contribute substantial fit gains (see Supplementary Tables 7 and 8).

Not all weather terms can be reliably projected by climate models^72,73,74 and models containing these candidate variables were explored in the cross-validation procedure (Extended Data Fig. 2) but ultimately excluded in projections of climate change because they could not be projected with reasonably high confidence. Overall, this procedure evaluates the out-of-sample (OOS) performance of candidate models that include all combinations of weather variables that we draw from the literature and allows for varying degrees of nonlinearity (Fig. 1, Extended Data Figs. 1a and 2 and Supplementary Information, sections B–D).

Cross-validation step two: selection of variables that capture adaptation

In our second cross-validation step, we select a set of covariate interactions for which covariates reflect the factors that mediate producer adaptation actions^{4,19,26,27,75,76} (equation (B.7)). We take as given the set of weather parameters selected from the first step, allowing for interactions between weather variables and income, irrigation, \(\bar{T}\), \(\bar{P}\) and/or \(\bar{T}\times \bar{P}\). Further, we allow for the nonlinear precipitation response to vary over phases of the growing season or to be constant over the growing season, with ‘phases’ of the growing season defined by a systematic model search (Supplementary Table 4). Finally, we also allow for interaction terms between degree day responses and monthly precipitation.

Accounting for mediating effects of income and irrigation is important because access to resources alters producer actions through several channels—such as access to technology^{77,78,79,80,81}, insurance and credit markets^77,80,82,83, inputs such as fertilizer^77,84 or labour markets^77,79,81 or information⁸⁵. Notably, this minimizes confounding in our estimates, as resources and climate tend to be correlated (for example, poorer nations tend to be located in the tropics⁸⁶) and it allows our model to capture that climate and income jointly determine yields⁸⁷. Further, this allows us to project future changes associated with economic development.

In this step, we use cross-validation with ten folds over random blocks of data grouped by state/province. Here the test of model performance is the ability to model yields for a set of states or provinces that are held out of the data. This matches one of the intended uses of our interaction surface, which is to model the heterogeneous response of yields to weather for locations with no yield data available.

In our climate projections, long-run average precipitation (\(\bar{P}\)) values range more than 17 standard deviations outside the mean in our historical data. To prevent extrapolating adaptation behaviour to \(\bar{P}\) values far outside our data, we imposed a single-knot linear spline in \(\bar{P}\) for each weather measure (\({z}_{a}(\bar{{P}_{i}})\), \({z}_{b}(\bar{{P}_{i}})\) and \({z}_{c}(\bar{{P}_{i}})\) below). These knots were chosen using a within-R² search over knot locations (Supplementary Information, section D). See Supplementary Information, sections B–D for further estimation details.

Example specification for maize

The final maize specification is:

with

in which y_it is log(yields) in administrative unit i in year t, \({{\rm{DD}}}_{it}^{8-31}\) represents degree days from 8 °C to 31 °C, which is interacted with each of average growing season daily maximum temperature (\({\bar{T}}_{i}\)), splines in average growing season total precipitation (\({z}_{[\cdot ]}({\bar{P}}_{i})\)), the interaction between \({\bar{T}}_{i}\) and \({z}_{[\cdot ]}({\bar{P}}_{i})\), average log(GDP_pc) (I_i) and area equipped for irrigation (R_i). The remaining weather terms have similar interactions. prcp_phase[j]_it represents monthly precipitation summed within growing-season-phase j, for j ∈ {1, 2, 3}. μ_i, h_s(t) and ρ_ct are as described previously. Standard errors of all estimated parameters allow for the correlated nature of yields (and weather) across space and over time. Specifically, we estimate cluster-robust standard errors⁸⁸, which allow arbitrary correlations across observations over time within first-level administrative units (that is, autocorrelations within and between counties within a given state) and across all observations within a given country–year. See ref. ³¹ for a discussion of this issue in this context. Note that the terms in equation (1) reflect rows (weather variables) and columns (mediating variables) illustrated in Extended Data Fig. 1b. See Supplementary Information, section D, for full details of the final model specification for each crop.

We note that the overall fit of the above empirical model to the historical data is high, with an R² of 0.85 for maize. For reference, the seminal analysis of maize by Schlenker and Roberts⁵ report a model R² of 0.77 when modelling yields for only the Eastern United States, for which data quality is high relative to much of the globe and the underlying patterns of producer behaviour are probably more homogeneous across locations.

Accounting for adaptation costs

We are able to empirically observe the benefits of adaptive management among producing regions because adaptation decisions have costs^19,26. If adaptations were free, then we would expect all regions to use uniform management practices and varieties using only the most climate-resilient technology available, as this strategy would convey benefits at no cost^19,29. To capture the full impact of climate change on agricultural systems, it is therefore essential that these costs of adaptation are accounted for, as well as adaptation benefits, as these costs would not be incurred in the absence of climate change.

We cannot observe these costs directly but they can be inferred under the assumption that profit-maximizing producers undertake adaptations for which the benefits exceed costs, but not those for which costs exceed benefits²⁹. This is referred to as a ‘revealed preference’ approach and is widely used in economics research⁸⁹. Specifically, we follow the approach developed in ref. ²⁹ to track these costs for each crop and in each region until 2100 (see Supplementary Information, section H, for a derivation, Supplementary Fig. 6 for intuition and Supplementry equations (H.6) and (H.7) for a detailed example). We follow ref. ¹⁹ and deduct these costs from yield changes to develop a complete measure of climate change impacts²⁹. Thus, our projections of climate change impacts on yields should be interpreted as capturing both the costs and the benefits of voluntary producer adaptations in each ___location.

Intuitively, consider the term \({\gamma }_{6}{\bar{T}}_{i}\) in equation (1), through which long-run average temperature in region i (\({\bar{T}}_{i}\)) modulates the negative effect of extreme heat shocks (\({{\rm{DD}}}_{it}^{31+}\)) on yields. A 1 °C increase in \({\bar{T}}_{i}\) flattens the negative extreme heat slope by γ₆ log points per extreme heat degree day—a benefit of adaptation in hotter climates. If a producer in this example expects ten extreme heat degree days during the growing season, then the expected adaptation benefit for a 1 °C increase in \({\bar{T}}_{i}\) would be 10 × γ₆ log points of yields. This benefit must not be costless, otherwise producers would have already adapted away all extreme heat yield losses. We thus infer marginal adaptation costs as equal to the marginal adaptation benefits that we estimate (an implication of assuming that producers maximize profits; see Supplementary Information, section H for details).

Model estimates

Weather variables that influence crop yields

Many correlated aspects of weather affecting crop biophysical processes have been separately studied^{2,5,36,67,68,69,70,71,101,102,103} and we evaluate which are important drivers of the biophysical processes affecting yields of each crop. We use cross-validation to evaluate more than 8,000 candidate empirical models across all six crops, for which each model predicts residual changes in historical crop yields using a different combination of weather variables proposed by previous studies^{5,67,68,69,70,71}. On the basis of OOS performance, we find that nonlinear degree days are the most important determinant of yields, on average across crops, by a considerable margin (Extended Data Figs. 1a and 2). Degree days increases model OOS fit (Supplementary Table 7) across crops by 51.7% on average (relative to the second-best model), with the largest gain for sorghum (101.6%, a doubling of model OOS fit) and the smallest gains for rice and cassava (9.1% and 9.4%). In general, exposure to cool daily temperatures (<9 °C for wheat and <29–31 °C for all other crops) modestly increase yields, whereas daily temperatures above these thresholds cause sharp declines in yields; for example, lowering end-of-season maize yields by −5% for each day that shifts from a 25 °C to a 40 °C day (Fig. 1g and Extended Data Fig. 3). This finding generalizes previous results from the USA (for example, see ref. ⁵) globally and across crops.

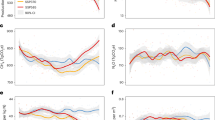
Seasonal precipitation is the second most important determinant of yields across all crops, to the exclusion of a wide range of other candidate weather variables put forward in the literature (Extended Data Figs. 1a and 2). Nonlinear measures of seasonal precipitation increase model OOS fit across crops by 14.5%, with the largest gains for rice and maize (22.8% and 22.2%) and the smallest gains for wheat, soybean and sorghum (7.8%, 9.2% and 9.4%; Supplementary Table 8). Across crops, increasing seasonal monthly precipitation raises yields on average 0.2% per mm at low rainfall levels (<100 mm per month), has little effect at intermediate levels (250–300 mm per month) and reduces yields −0.6% per mm at higher levels (>400 mm per month; Extended Data Figs. 3 and 4).

In contrast to reports from individual empirical studies (for example, refs. ^67,68,69,71), we find that monthly average minimum temperatures (t_min), vapour pressure deficit, drought, the count of rain days, the count of extreme rain days and the amount of extreme rain generally only contribute modest gains to yield model fits (average % gains in OOS fit range from 1.2% to 3.6% excluding drought for cassava, discussed below). Minimum temperatures are important predictors for rice and wheat yields but not other crops (Extended Data Fig. 2 and Supplementary Tables 7 and 8).

There are exceptions for individual crops. Cassava yields are generally insensitive to weather overall (the maximum OOS variance predicted is 2.3%), motivating its cultivation in contexts in which the climate is not conducive to other staple crops that are more sensitive¹⁰⁴. We find that growing season drought is the most important factor for predicting cassava yields (24.0% gain in variance predicted; Supplementary Table 7). Drought is also important for rice yields, as is the count of rain days (6.4% and 8.0% gain in variance predicted; Supplementary Table 7). The count of rain days is also moderately important for maize yields (6.6% gain in variance predicted; Supplementary Table 7). Taken together, these results indicate the importance of nuanced projections of future precipitation distributions for a restricted set of global staple crops.

Adaptation to climate

We find that producers adapt to higher temperatures such that, across crops and around the world, yields are systematically less sensitive to daily temperature and generally more sensitive to seasonal precipitation in locations that are hotter on average (Fig. 1 and Extended Data Figs. 1b, 3a,e and 4a,e). Similarly, yields are less responsive to temperature and more responsive to precipitation in locations that are drier on average (Extended Data Figs. 1b, 3b,f and 4b,f). Because climate-associated adaptations influence numerous—possibly correlated—aspects of weather–crop responses, we estimate the mediating influence of all dimensions of climate simultaneously on all dimensions of weather for each crop, generating a multidimensional function describing these interacting relationships (Extended Data Figs. 3 and 4). This function serves as the basis for projecting adaptation to climate change (Methods and Supplementary Figs. 4 and 5) and has not been previously represented in global process-based models^7,8.

Economic development

We also find that rising incomes enable producers to respond to environmental conditions in important but varied ways, thereby mediating the effects of different climates. For example, maize and sorghum yields become more sensitive to temperature as incomes rise, whereas rice and cassava become less sensitive (Extended Data Figs. 1b and 3c). These differences could be because of differences in how access to improved technologies, infrastructure, banking and credit or insurance^77,78,80,82 influence producer strategies^77,83. Notably, however, we find that higher incomes and access to irrigation are associated with greater resilience to precipitation extremes across all crops (Extended Data Figs. 1b, 3g and 4g), consistent with access to improved irrigation technologies increasing with income^77,80.

Projections and the partial SCC

We integrate our econometric results with the DSCIM^28,29 to develop projections and partial SCC estimates (Supplementary Information, section K.5). Calculations were conducted as described in refs. ^28,29, over 24,378 geographically granular regions, 33 climate models and 1,920 Monte Carlo draws of statistical uncertainty per crop. Following ref. ²⁹, we project the impacts of climate change net of adaptation and its costs, relative to a counterfactual in which incomes grow but the climate is held fixed. Projections in percentage terms represent weighted averages of log yield estimates, converted to percentages. Crop impacts are aggregated over space using cropped area weights (Supplementary Information, section A), over climate models using surrogate model mixed ensemble⁶¹ weights (Supplementary Table 9) and over crops using calorie weights⁹⁰. Yield gains from CO₂ fertilization are difficult to empirically quantify^91,92,93,94 but we adjust our projections to incorporate CO₂ fertilization using previous estimates⁹. Yield projections are robust to restricting future weather projections to be bound within the support of the historical data (Supplementary Table 12 and Supplementary Fig. 12). See Supplementary Information, section G for full details of the projection methodology.

To calculate a partial SCC, we must value climate-induced changes in yields for both producers and consumers (Supplementary Figs. 19 and 21). Our approach to this valuation follows ref. ⁹⁵ and models consumers and producers of calories with constant elasticity of demand and supply, drawing elasticities from the literature^95,96,97. We allow for frictionless crop trade within country but do not allow for trade between countries. We test sensitivity to this assumption by allowing frictionless trade between countries within continents and throughout the globe. We consider the potential impacts of crop switching, shifting of cropped areas and international trade by drawing on the previous model-based literature^75,98,99,100. In calculating the SCC, we follow ref. ²⁸ to calculate results for constant discount rates (2%, 2.5%, 3%, 5%) and refs. ^28,47 for Ramsey discounting (ρ = 0, η = 2). See Supplementary Information, section K, for full details of the valuation methodology.

Methodological challenges

A challenge to this analysis is the limited way in which future resource access has been projected¹⁰⁵, that is, relying on standardized scenarios contained in the SSPs⁶⁵. Numerous types of resources probably influence how staple crops are managed. However, we restricted our analysis to consider only the mediating effects of income and irrigation. We treat income as a proxy measure for access to resources associated with economic development, such as fertilizer or extension services. These variables are intentionally omitted from regression models so that their influence will be captured by the income variable, allowing them to be represented in standard socioeconomic projections for which income is projected and available to us, but these other variables are not⁶⁵. Mediating effects of irrigation are accounted for explicitly because they are influential and irrigation presence is dependent on groundwater geology, local topography and surface water flows, which are not well captured by income nor climate measures. An important area for future work is to develop projections of irrigation for use in crop yield projections.

Another challenge is that our measures of climate used to estimate adaptation are cross-sectional; thus, correlations between climate and omitted variables that determine the shape of the yield–weather response could potentially bias our estimates of adaptation. If such correlations exist, they might be regional in nature or otherwise only affect limited subsamples of our data. As a partial test of this possibility, we examine non-parametric estimates of the association between climate and temperature sensitivity and find that the associations we rely on are systematic throughout the data (Supplementary Fig. 3). This suggests that any unknown omitted variable would have to be consistently correlated with climate throughout our sample to influence our analysis.

We are able to account for some, but not all, potential shifts in crop growing seasons under future climate change. Our parameterization of adaptation implicitly captures effects of shifting the harvest date earlier in the growing season (for example, to avoid late-season heat exposure; see Supplementary Information, section B). However, we cannot capture the effects of planting dates that may shift to a period before the start of our growing season windows nor can we capture crop switching in our yield models (although we do capture it in the valuation of impacts; see Supplementary Information, section K). We note that such shifts may not depend only on temperatures but also on rainfall quantity and timing, which are not yet well modelled by existing GCMs^72,73,74. These are forms of adaptation that some process-based models explicitly include^{7,8,9,18,106,107,108}. Furthermore, unlike process-based models, our reduced-form approach by design does not capture the agronomic mechanisms by which climatic changes influence future yields. Such mechanistic insights can be used to guide crop research in expectation of future climate stresses^41,42,43,44, highlighting an important trade-off in the two methodological approaches (Supplementary Information, section B.1).

For precipitation effects, we do not project some extreme precipitation effects because these precipitation extremes are not well captured by the existing suite of GCMs^72,73,74. We highlight this as an area of need for future research from the climate modelling community, with potentially important implications for our further understanding of climate change impacts to global food security.

Also, we note that our valuation of agricultural damages from climate change and the partial SCC only accounts for the crops in our sample, which account for a large share of global calories but a smaller share of total agricultural revenues. The present analysis does not include effects of climate change on other sources of agricultural revenue, such as livestock, citruses and other specialty crops. We look to future work to incorporate these output categories.