Introduction

An optimization problem involves determining the best or a sufficiently good approximate solution from numerous possible options or parameter combinations, all under specific constraints. The core objective is to find the solution that maximizes or minimizes an objective function from a set of feasible solutions. In engineering applications, as the complexity and scale of problems continue to grow, traditional optimization methods, such as linear programming, steepest descent, conjugate gradient, and penalty function methods, have become inadequate for addressing complex problems or situations that require high-precision solutions. Traditional optimization algorithms often struggle with complex problems characterized by nonlinearity, multimodality, high dimensionality, and non-convexity. They tend to fall into local optima, with outcomes highly dependent on initial values. To overcome these challenges, many researchers have turned to biological, natural, and social phenomena for inspiration. By analyzing the key characteristics of these phenomena-such as cooperation, information sharing, and specialized behaviors-scholars have developed metaheuristic algorithms that simulate these dynamics, offering more robust solutions for complex optimization tasks. Metaheuristic algorithms have demonstrated significant potential in solving real-world problems and have been widely applied across various domains,including industry1,2, military3,4 , transportation and logistics5,6,7,8, and engineering9,10,11,12.

Meta heuristic optimization algorithms can be mainly divided into four categories: evolutionary based algorithms, swarm intelligence based algorithms, human based algorithms, and physics and chemistry based algorithms Evolutionary algorithms mainly simulate the natural law of survival of the fittest to achieve overall population progress and ultimately solve for the optimal solution. To find the optimal solution to a problem by simulating mechanisms such as genetics, crossover, and mutation in biological evolution. The core idea of swarm intelligence based algorithms is to simulate the collective intelligence of biological populations in order to find the global optimal solution. In this algorithm, each population is regarded as a vivid biological population, and each individual in the population collaborates and cooperates with each other to perform tasks that are difficult to accomplish solely by individual strength. Algorithms based on human behavior mainly draw inspiration from various behavioral patterns in human daily life. These algorithms simulate various human behaviors such as teaching, socializing, learning, emotions, and management. Physics and chemistry based algorithms mainly come from physical rules and chemical reactions in the universe, such as lightning, water waves, sound, gravity, and chemical reactions. In recent years, metaheuristic algorithms have been applied and developed in multiple fields, and among the four types of algorithms, the swarm intelligence algorithm used to simulate biological populations has received the most attention and research from scholars. Due to the lack of the No Free Lunch theorem (NFL), it is known that for all possible optimization problems, no algorithm is superior to other algorithms in all problems. The design of optimization algorithms needs to be adjusted and optimized for specific problems, and there is no universal algorithm that can perform best in all situations.

Constrained optimization problems in engineering design have become a key application area for intelligent optimization algorithms. These problems involve finding the optimal design solutions while satisfying multiple constraints related to technical, economic, and other factors. Yan et al.13 proposed a hybrid genetic algorithm that enhances the algorithm’s ability to escape local optima. Through validation on three practical engineering problems, the study demonstrated the algorithm’s strong convergence accuracy and robustness. Gong et al.14 introduced a multi-objective differential evolution algorithm for addressing engineering design problems and utilized it to solve four engineering design optimization problems. The results demonstrate the efficiency and applicability of the algorithm in multi-objective design optimization. Akay et al.15 proposed an artificial bee colony algorithm for large-scale problems and applied it to optimize five constrained engineering problems, showcasing its superiority in handling large-scale problems.Li et al.16proposed a moth flame algorithm based on the Levy-flight strategy to increase population diversity, enabling the algorithm to effectively escape local optima. The algorithm’s effectiveness was demonstrated in solving two constrained engineering design problems. Sayed et al.17 proposed a hybrid algorithm based on Moth Flame Optimization (MFO) and Simulated Annealing (SA), which was applied to four well-known constrained engineering problems. Experimental results demonstrate the superiority of the proposed algorithm. Furthermore, Chen et al.18 introduced Levy flight and chaotic local search into the Whale Optimization Algorithm, enhancing convergence speed and solution quality for three traditional engineering optimization problems. Rizk-Allah19 presented a multi-orthogonal search strategy combining sine-cosine algorithm with orthogonal search, improving convergence speed and stability. The algorithm was applied to four engineering design problems to study its performance. Yi et al.20 proposed a parallel chaotic local search-enhanced Harmony Search Algorithm for solving engineering design optimization problems. It was applied to constrained engineering design problems, proving its effectiveness. El-Shorb et al.21 combined genetic algorithm with firefly algorithm to prevent falling into local optima while balancing exploration/exploitation trends. The algorithm’s superiority was verified by solving seven engineering design problems. Pathak et al.22 introduced an upgraded Bat Algorithm with Cuckoo Search and Sugeno inertial weights to address the limitations of the Bat Algorithm in solving multi-dimensional engineering problems, such as being trapped in local minima and slow convergence. The proposed algorithm demonstrated higher optimization accuracy and faster convergence when solving seven well-known constrained engineering design problems.

Spider Wasp Optimization (SWO), introduced by Mohamed Abdel Basset et al. in 2023, is inspired by the hunting, nesting, and mating behaviors of female spider wasps in nature. This algorithm boasts advantages such as fast search speed and high solution accuracy. With several unique update strategies, it is well-suited for a wide range of optimization problems requiring different levels of exploration and exploitation. Despite its strengths, SWO has some limitations, including low convergence accuracy, slow convergence speed, and a tendency to become trapped in local optima. To overcome these shortcomings, future research will focus on improving the algorithm’s adaptability and optimization capabilities. The enhanced SWO will be applied to address real-world problems across various fields.

To better suit practical engineering applications and achieve faster convergence to optimal solutions, a Multi-strategy Improved Spider Wasp Optimization is proposed. To address the drawbacks of the original algorithm, such as slow convergence speed and low accuracy in the early stages, the Grey Wolf Algorithm23 s introduced during the initialization phase. This enhancement improves the convergence rate and fitness of the initial population, optimizing the starting state and providing a more advantageous beginning for the entire optimization process, thereby boosting the algorithm’s global optimization capability.

Additionally, to overcome the inefficiency caused by randomly selecting the search range in the original algorithm, an adaptive step size operator24 is incorporated into the search phase. This operator automatically adjusts the search range of spider bees at different optimization stages, enhancing the efficiency and effectiveness of the search process. Simultaneously, Gaussian mutation is introduced to enhance the algorithm’s optimization accuracy and its ability to escape local optima. In the original algorithm, manually setting the trade-off rate (TR) parameter can result in significant variations in optimization outcomes for slightly different TR values. To address this issue, a dynamic selection of the trade-off rate (TR) is implemented, enabling a more flexible trade-off strategy throughout the algorithm’s execution. Finally, a dynamic lens imaging reverse learning strategy is introduced to adjust the parameters of lens imaging in response to reverse solution changes, providing a more accurate target position for the algorithm. This approach reduces the algorithm’s search blindness and significantly enhances optimization accuracy. The proposed algorithm is compared with several of the latest and most frequently cited optimization algorithms. Experimental evaluations on 23 complex benchmark test functions and 7 engineering optimization problems show that it outperforms other algorithms in terms of optimization capability, stability, and applicability to various problems. This demonstrates the algorithm’s excellent performance across a wide range of application fields and its effectiveness in handling complex and diverse problem scenarios.

The main contributions of this paper can be summarized as follows:

1. A Multi-strategy Improved Spider Wasp Optimization algorithm is proposed, enhancing its applicability and development capabilities through the integration of wolf pack initialization, an adaptive step size operator, a dynamic trade-off rate, and a dynamic lens imaging reverse learning strategy.

2. The MISWO algorithm demonstrated superior performance compared to a selection of advanced optimization algorithms across 23 benchmark test functions. Statistical experimental results validate its effectiveness and superiority.

3. The algorithm successfully solved 7 engineering problems of varying complexity in real-life scenarios, confirming its practicality. Comparative analysis using data further illustrates the algorithm’s advancement over selected algorithms.

In summary, this article is divided into the following parts. “Multi-strategy improved spider wasp optimization” enhances Spider Wasp Optimization by integrating multiple strategies to develop a Multi-strategy Improved Spider Wasp Optimization (MISWO) algorithm, and provides a detailed flow of the improved algorithm. “Simulation experiment and analysis” compares the performance of the MISWO algorithm with various advanced algorithms across 23 benchmark test functions and presents the test results. “Engineering optimization problems and analysis” presents seven engineering problems of varying complexity and uses the MISWO algorithm to solve them. Additionally, it includes experimental results from simulations of paired unmanned aerial vehicles navigating disaster-affected mountain maps of different complexities. “Conclusion” summarizes the findings of the article and proposes ideas for future improvements.

Multi-strategy improved spider wasp optimization

This section provides an overview of how the Grey Wolf algorithm is used to enhance the quality of the initial population. It also introduces dynamic inertia weights during the search, chase, and escape stages to dynamically adjust the trade-off rate (TR). Additionally, a reverse learning strategy for dynamic lens imaging is introduced to highlight its mechanisms.

Initialization of the grey wolf algorithm population

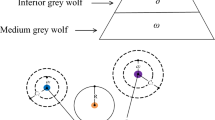
Grey wolves, belonging to the canidae family, are top predators and occupy the apex of the food chain. They typically live in packs of 5 to 12 individuals and have a highly structured social hierarchy. In 2014, Mirjalili et al. introduced a new swarm intelligence algorithm inspired by the behavioral characteristics of grey wolves: Grey Wolf Optimization (GWO). GWO mimics the predation behavior of grey wolf packs and achieves optimization through mechanisms of pack cooperation. GWO categorizes wolf packs into four levels based on priority: \(\alpha\), \(\beta\), \(\delta\), and \(\omega\), to carry out a series of activities including searching for prey, surrounding prey, and attacking prey. The \(\alpha\) wolf is the leader of the wolf pack, mainly responsible for making decisions about hunting, sleeping time and place, food allocation, and other aspects of the group. The \(\beta\) wolf is mainly responsible for assisting the \(\alpha\) wolf in making decisions, issuing commands from the \(\alpha\) wolf to other members, and providing feedback on the execution status of other members to the \(\alpha\) wolf, playing a bridging role. When there is a vacancy in the \(\alpha\) wolf of the entire wolf pack, the \(\beta\) wolf will take over the position of the \(\alpha\) wolf. The \(\delta\) wolf follows the decision-making commands of the \(\alpha\) and \(\beta\) wolves and is mainly responsible for reconnaissance, surveillance, and care. \(\alpha\) wolves and \(\beta\) wolves with poor adaptability will also be downgraded to \(\delta\) wolves. \(\omega\) wolves are primarily responsible for maintaining the balance of relationships within their population. The formula for surrounding prey by the wolf pack after identifying it is given by:

$$\begin{aligned} & \begin{aligned} D=\left| C \cdot X_p(t)-X(t)\right| \end{aligned} \end{aligned}$$
(1)
$$\begin{aligned} & \begin{aligned} X(t+1)=X_p(t)-A \cdot D \end{aligned} \end{aligned}$$
(2)

Let t represents the iteration number,\(X_p(t)\) denotes the information of the prey,Xp(t) and \(Xp(t+1)\)represent the positions of the grey wolf before and after the update, respectively. D indicates the distance between the prey and the grey wolf.A and C are coefficients used to balance the algorithm’s exploration and exploitation capabilities. The formula is as follows:

$$\begin{aligned} & \left\{ \begin{array}{c} A=2 a r_1-a \\ C=2 * r_2 \end{array}\right. \end{aligned}$$
(3)
$$\begin{aligned} & a=2-\frac{2 t}{t_{\max }} \end{aligned}$$
(4)

\(r_1\) and \(r_2\) are random numbers between [0,1]. t represents the iteration number, \(t_max\) denotes the maximum number of iterations. The wolf pack adjusts its positions under the leadership of the \(\alpha\), \(\beta\), and \(\delta\), wolves to attack the surrounded prey. As shown in Fig. 1:

Figure 1
figure 1

Grey wolf packs attack surrounded prey.

Full size image

In each iteration, the best value obtained is assigned to \(\alpha\), \(\beta\), and \(\delta\) Ordinary wolves adjust their positions based on the positions of the leading wolves to complete the surrounding and hunting behaviors. The formula is as follows:

$$\begin{aligned} & \left\{ \begin{array}{l} D_\alpha =\left| C_1 X_\alpha (t)-X(t)\right| \\ D_\beta =\left| C_1 X_\beta (t)-X(t)\right| \\ D_\delta =\left| C_1 X_\delta (t)-X(t)\right| \end{array}\right. \end{aligned}$$
(5)
$$\begin{aligned} & \left\{ \begin{array}{l} X_1=X_\alpha (t)-A_1 D_\alpha \\ X_2=X_\beta (t)-A_1 D_\beta \\ X_3=X_\delta (t)-A_3 D_\delta \end{array}\right. \end{aligned}$$
(6)

\(D_\alpha , D_\beta\) and \(D_\delta\) respectively represent the distances between the alpha,beta,and delta wolves and other wolves, \(X_1, X_2, X_3\) denote the movement changes that occur in other wolves influenced by the alpha,beta,and delta wolves.

In the initialization phase of SWO, each spider wasp represents a solution. A spider wasp individual with d dimensions can be represented as follows:

$$\begin{aligned} \overrightarrow{S W}=\left[ x_1, x_2, x_3, \ldots x_d\right] \end{aligned}$$
(7)

A population of size N is randomly generated within the search space [L, U] as follows:

$$\begin{aligned} \left[ \begin{array}{cccc} s w_{1,1} & s w_{1,2} & \ldots & s w_{1, d} \\ s w_{2,1} & s w_{2,2} & \ldots & s w_{2, d} \\ \vdots & \vdots & \vdots & \vdots \\ s w_{N, 1} & s w_{N, 2} & \ldots & s w_{N, d} \end{array}\right] \end{aligned}$$
(8)

In the search space, arbitrary solutions are randomly generated using the following formula.

$$\begin{aligned} \overrightarrow{S W}_{\textrm{i}}^t=\textbf{L}+\textbf{r} *(\textbf{H}-\textbf{L}) \end{aligned}$$
(9)

Where t represents the generation index, \(i(i=1,2,3, \ldots , N)\) represents the population index, and \(\textbf{r}\) is a vector of d dimensions containing numbers between 0 and 1.

Due to the strong population diversity of the spider wasp optimization (SWO) algorithm, ensuring the search for the optimal solution, its convergence performance is often compromised. To address this limitation, a hybrid strategy leveraging the strong convergence capability of the gray wolf optimization (GWO) algorithm is proposed. This strategy aims to initialize the spider wasp population using the GWO algorithm, which results in a more concentrated initial population distribution and provides clearer optimization directions, thus accelerating the convergence speed of the algorithm. After generating a random population using Equation (27), the SWO algorithm undergoes population updating through the GWO algorithm to obtain a new spider wasp population.

$$\begin{aligned} & \overrightarrow{S W_{\textrm{I}}}=\textbf{L}+\textbf{r} *(\textbf{H}-\textbf{L}) \end{aligned}$$
(10)
$$\begin{aligned} & \overrightarrow{G_{\textrm{I}}}=F_l\left( \overrightarrow{S W_{\textrm{i}}}\right) \end{aligned}$$
(11)

\(\overrightarrow{S W_{\textrm{i}}}(i=1,2,3, \ldots , N)\) epresents the randomly generated initial population, and \(F_l\) denotes the iteration using the gray wolf algorithm for l times. This process results in the initial population of spider wasps.

Adaptive step size operator and dynamic trade-off rate

In the hunting behavior of the Spider Wasp Optimization (SWO) algorithm, two distinct step sizes are randomly employed to explore the solution space: a large-step search to maintain the population’s global search capability, and a small-step search to focus on exploring the vicinity of known solutions. Female wasps persistently explore the search space with a constant large step size in search of suitable spiders for their offspring. This behavior can be mathematically formulated as follows:

$$\begin{aligned} {\overrightarrow{S W_{\textrm{i}}}}^{t+1}={\overrightarrow{S W_{\textrm{i}}}}^t+\mu _1 *\left( {\overrightarrow{S W_a}}^t-{\overrightarrow{S W_b}}^t\right) \end{aligned}$$
(12)

Where a and b are two randomly selected indices from the population. \(\mu _1\) controls the direction of movement of the spider wasp. the formula is given by:

$$\begin{aligned} \mu _1=|r n| * r_1 \end{aligned}$$
(13)

\(r_1\) is a randomly generated number within the range [0,1], while rn represents a random number generated from a normal distribution. Additionally, a small step size is employed to explore the area surrounding the dropped spider. The formula is given by:

$$\begin{aligned} {\overrightarrow{S W_i}}^{t+1}={\overrightarrow{S W_{\textrm{c}}}}^t+\mu _2 *\left( \textbf{L}+\textbf{r}_2 *(\textbf{H}-\textbf{L})\right) \end{aligned}$$
(14)

A randomly selected individual from the population, where C is the index of the randomly selected individual. \(\mu _2\) is a random number generated by the following formula:

$$\begin{aligned} \mu _2=B * \cos (2 \pi l) \end{aligned}$$
(15)

l is a randomly generated number between 1 and -2. B is a random number generated by the following formula:

$$\begin{aligned} B=\frac{1}{1+e^l} \end{aligned}$$
(16)

The spider wasp optimization (SWO) algorithm employs two randomly selected search methods to update the population. However, both methods utilize a fixed step size during exploration, which constrains the algorithm’s ability to swiftly identify high-quality solutions in the early stages and impacts its convergence accuracy in the later stages. To overcome this limitation, an adaptive step size operator, denoted as h, is introduced during the search phase. This operator ensures adequate global search capability in the early stages while improving convergence speed in the later stages. The formula for the adaptive step size operator is as follows:

$$\begin{aligned} h=\left( e^{-\sqrt{\frac{t}{t_{\max }}}}\right) ^{20} \end{aligned}$$
(17)

Where t represents the current iteration number, and \(t_{\max }\) denotes the maximum iteration number of the algorithmAs individuals gradually approach the optimal solution region, the search space will shrink, which may cause the algorithm to become trapped in local optima. To mitigate this issue, Gaussian mutation is introduced. The Gaussian mutation strategy utilizes the Gaussian (normal) distribution to generate mutation vectors. This distribution has a higher probability of producing data points near the mean, with the likelihood decreasing as points deviate from the mean. This feature allows the algorithm to conduct a fine search in the vicinity of the current optimal solution, thus improving its local search capability. When the algorithm becomes trapped in a local optimum, Gaussian mutation can guide the algorithm to fine-tune the search within the local region, potentially enabling it to escape from the local optimum. The formulas for incorporating Gaussian mutation into the adaptive step size operator and the search phase are as follows:

$$\begin{aligned} \left\{ \begin{array}{c} \overrightarrow{S W}_{\textrm{i}}^{t+1}=\left( \overrightarrow{S W}_{\textrm{i}}^t+\mu _1 *\left( {\overrightarrow{S W_a}}^t-{\overrightarrow{S W_b}}^t\right) * h\right) +{ Gauss} \\ \overrightarrow{S W}_{\textrm{i}}^{t+1}=\left( \overrightarrow{S W}_{\textrm{c}}^t+\mu _2 *\left( \textbf{L}+\overrightarrow{r_2} *(\textbf{H}-\textbf{L})\right) * h\right) +{ Gauss} \end{array}\right. \end{aligned}$$
(18)

Where Gauss refers to a random number sampled from a Gaussian distribution. The adaptive step size operator dynamically adjusts step sizes according to the iteration process, effectively balancing exploration and exploitation throughout the algorithm. In SWO, mating behavior is employed to generate spider wasp offspring, which represent potential solutions for the current generation. The offspring generation formula is as follows:

$$\begin{aligned} \overrightarrow{S W}_{\textrm{i}}^{t+1}= \text{ Crossover } \left( \textrm{SW}_{\textrm{i}}^{\textrm{t}}, \textrm{SW}_{\textrm{m}}^{\textrm{t}}, \textrm{CR}\right) \end{aligned}$$
(19)

\(\beta\) and \(\beta _1\) are two numbers generated randomly from a normal distribution, while\(\overrightarrow{v_1}\)and \(\overrightarrow{v_2}\) are generated using the following formulas.

$$\begin{aligned} \begin{aligned} \overrightarrow{v_1}=\left\{ \begin{array}{c} \textbf{x}_a-\textbf{x}_i f\left( \textbf{x}_a\right)<f\left( \textbf{x}_i\right) \\ \textbf{x}_i-\textbf{x}_a \text{ otherwise } \end{array}\right. \\ \overrightarrow{v_2}=\left\{ \begin{array}{c} \textbf{x}_b-\textbf{x}_c f\left( \textbf{x}_b\right) <f\left( \textbf{x}_c\right) \\ \textbf{x}_c-\textbf{x}_b \text{ otherwise } \end{array}\right. \end{aligned} \end{aligned}$$
(20)

Where a,b,c are indices randomly selected from the population such that \(a=i>b>c\). The hybridization process generates offspring that inherit characteristics from their parents. The trade-off rate (TR) governs the balance between hunting and mating behaviors. The corresponding formula is as follows:

$$\begin{aligned} \left\{ \begin{array}{c} F(H) \text{ or } F(N) \text{ rand } <T R \\ F(M) \text{ otherwise } \end{array}\right. \end{aligned}$$
(21)

Where F(H) or F(N) represents hunting or nesting behavior, and F(M) represents mating behavior.The selection of the trade-off rate significantly influences the optimization capability of SWO. In SWO, manually adjusting the trade-off rate multiple times with a constant value is inefficient and limits the effective utilization of the algorithm. To address this issue, a nonlinear adaptive step size operator is proposed, which dynamically selects the trade-off rate as the iterations progress. The description of the adaptive step size operator is as follows:

$$\begin{aligned} T R_n=1-\left( e^{\left( \sqrt{\frac{t}{t_{\max }}}-1\right) * {\text {rand}}()}\right) \end{aligned}$$
(22)

The new balance rate will gradually decrease from 1 to 0 as the iterations progress, while retaining a certain level of randomness.

Dynamic lens imaging reverse learning strategy

Reverse learning computes the reverse solution based on the current population’s positions, expanding the search space. Integrating this strategy with swarm intelligence algorithms can significantly enhance optimization performance and expedite convergence to the optimal solution. However, in later iterations, reverse learning may become less effective at helping the algorithm escape local optima, which could lead to reduced convergence accuracy. Furthermore, the choice of parameters in reverse learning is critical to the algorithm’s overall performance. To address these challenges, a dynamic lens imaging reverse learning strategy is proposed, inspired by the principles of convex lens imaging. As illustrated in Figure 2, within a two-dimensional coordinate system, the search range along the x-axis is defined as [a,b], while the y-axis depicts a scenario influenced by a nonlinear convex lens effect. Consider an object A with a projection x on the x-axis and a height h. The lens effect results in the formation of an image A* on the opposite side after passing through the lens, where the projection of A on the x-axis remains x, but its height is transformed to h*. The formula for lens imaging reverse learning can be articulated as follows:

$$\begin{aligned} \frac{\frac{a+b}{2}-x}{x^*-\frac{a+b}{2}}=\frac{h}{h^*} \end{aligned}$$
(23)

The above formula can be transformed into:

$$\begin{aligned} x^*=\frac{(a+b)}{2}+\frac{(a+b)}{2 k}-\frac{x}{k} \end{aligned}$$
(24)

The parameter\(k=\frac{h}{h^*}\) is used to control the magnitude of the reflection. When k=1, the formula becomes:

$$\begin{aligned} x^*=a+b-x \end{aligned}$$
(25)

This is the formula for the reverse learning strategy.

Figure 2
figure 2

Principle of reverse learning strategy for lens imaging.

Full size image

In lens imaging reverse learning, dynamic variations of the reverse solution are achieved by flexibly adjusting the parameter k, significantly enhancing the algorithm’s optimization precision. When the parameter k takes a small value, the range of generated reverse solutions is larger; whereas when k takes a larger value, the generated reverse solutions are limited to a smaller range. The dynamic adjustment parameter k used in this paper is as follows:

$$\begin{aligned} k=\left( 10^3+\left( \frac{3 t}{t_{\max }}\right) ^{\frac{1}{2}}\right) ^{10} \end{aligned}$$
(26)

By adjusting the value of k, the size of the solution space explored during reverse learning can be controlled. When k is small, the algorithm is more exploratory, capable of searching potential optimization solutions across a wide solution space. Conversely, when k is large, the focus of reverse learning is more concentrated within a local range, which is conducive to a more in-depth exploration of the details within that local area. The pseudocode for the MISWO algorithm can be found in Algorithm 1, and the corresponding flowchart is shown in the following Fig. 3. To address the shortcomings of the original Spider Wasp Optimization (SWO), several improvement methods have been introduced to enhance algorithm performance. The process begins with the initialization of the MISWO parameters. Unlike random initialization, the Grey Wolf Algorithm is used to set up the population, ensuring better initial conditions. The trade-off rate is determined using the dynamic adaptive step size operator, which helps to choose between hunting and nesting behavior or mating behavior. When hunting and nesting behavior is selected, the search stage is managed by the adaptive step size operator and enhanced with Gaussian mutation. On the other hand, if mating behavior is chosen, the population is updated accordingly. After the population update, the lens imaging strategy is applied to map the population and generate the inverse solution, which is then selectively preserved using a greedy strategy. The fitness values of the population are calculated and stored in memory. To further enhance efficiency, the population size is reduced, speeding up the optimization process. The algorithm iterates until the optimal value is reached. If the stopping condition is met, the final output is the optimal solution; otherwise, the algorithm continues to iterate.

Algorithm 1
figure a

The MISWO.

Full size image
Figure 3
figure 3

MISWO flowchart.

Full size image

Simulation experiment and analysis

Algorithmic procedure of MISWO

To validate the overall performance of the Multi-strategy Improved Spider Wasp Optimization (MISWO) algorithm, this section evaluates its effectiveness on 23 fundamental benchmark functions commonly used in the literature25. These functions cover a range of dimensions, from low to high, and include both single-peak and multi-peak scenarios, as detailed in Table 1. The MISWO algorithm is compared with several state-of-the-art and widely cited optimization algorithms, including the Arithmetic Optimization Algorithm (AOA)26, Harris Hawk Optimization (HHO)27, Whale Optimization Algorithm (WOA)28, Grey Wolf Optimization (GWO), White Shark Optimizer (WSO)29,Coronavirus herd immunity optimizer(CHIO)30, Particle Swarm Optimization (PSO), and the original Spider Wasp Optimization (SWO) algorithm22. To ensure a fair and objective comparison, all algorithms are executed under the same software and hardware conditions, specifically using a Windows 10 operating system and the MATLAB R2023a programming environment. The evaluation begins with high-dimensional single-peak functions (F1-F7), which have only one global solution and no local minima. These functions assess the exploitation capability of MISWO. For these functions (F1-F5), a population size of 30 and a maximum of 4000 iterations are used for each algorithm, which is fewer iterations compared to the original algorithm’s count of\(\left( 5 \times 10^4\right)\). For F6-F23, the maximum iteration count remains at \(5 \times 10^4\) to reduce randomness interference, and each algorithm is run independently for 30 times. The results are shown in Table 2.

The data presented in Table 2 shows that MISWO consistently achieves the optimal solution for benchmark functions F1 to F4, with both its average and worst fitness values being the best among the compared algorithms. Moreover, MISWO converges to the optimal solution more quickly than the original algorithm, requiring fewer iterations. For F5, although MISWO’s performance does not surpass HHO, it still outperforms the original algorithm and most other optimization algorithms in terms of optimal, average, and worst fitness values. Additionally, MISWO delivers the best overall performance for F6 and F7, achieving the highest accuracy in average, optimal, and worst fitness values across these functions. Functions F8 to F13 are multimodal, containing multiple extrema, and are designed to test the algorithm’s ability to escape local minima and locate global optima. As seen in Table 2, HHO achieves the best, average, and worst fitness values for F8, but MISWO still outperforms the remaining algorithms. For F9 to F11, MISWO finds the optimal solution with both the worst and average values also being optimal. In F12, while MISWO does not find the optimal solution, its results surpass all algorithms except for PSO and WSO. For F13, MISWO achieves the optimal solution for the best, worst, and average values. Finally, F14 to F23 are fixed-dimensional multimodal functions used to evaluate the algorithm’s performance in fixed dimensions and further assess its adaptability. MISWO consistently secures the best, average, and worst fitness values for F14 to F20, demonstrating strong consistency. For F21, MISWO finds the optimal value, though its worst value is not optimal. However, in F22 and F23, MISWO continues to deliver optimal and consistent best, average, and worst fitness values.

Based on the results of the test functions, MISWO consistently demonstrates near-globally optimal performance across single-peak functions, multi-peak functions, and fixed-dimensional multi-peak functions. The outcomes from the single-peak functions reveal MISWO’s robustness and strong exploration capabilities. By enhancing the original algorithm’s exploration ability, MISWO also accelerates convergence, allowing it to locate the optimal solution more rapidly. The results from the multi-peak functions highlight MISWO’s capacity to escape local optima and achieve global optimization. When compared to other algorithms and the original version, MISWO consistently delivers superior optimal, average, and worst fitness values. Moreover, the fixed-dimensional multi-peak function results further validate MISWO’s exceptional adaptability, stability, and problem-solving capabilities, as it maintains optimal fitness values and consistency across various test functions.

Table 1 Test functions F1-F23.
Full size table
Table 2 Comparison of Optimization Performance of Algorithms.
Full size table

Convergence curve analysis

Convergence curves visually depict an algorithm’s convergence speed, accuracy, and optimization capabilities, providing a straightforward comparison across different functions. These curves help assess the algorithm’s efficiency and its ability to search for optimal solutions within the solution space. Presented here are the convergence curves for the 23 test functions discussed earlier. The number of iterations and parameters used are consistent with those in the previous section. For better clarity, some individual graphs are magnified. In certain cases, curves may overlap or show substantial differences in results, making it difficult to display all curves distinctly.

The convergence curves of the F1–F23 test functions are illustrated in Fig. 4. A more intuitive analysis of these curves reveals several key insights: for the unimodal functions F1–F4, although most algorithms, aside from the original one, can achieve the optimal solution, MISWO consistently converges to this optimal solution at the fastest rate. Additionally, aside from F5 and F7 where HHO achieves the optimal value, and F6 where PSO finds the optimal solution, MISWO still demonstrates the highest convergence speed, securing suboptimal solutions.

In multimodal functions, MISWO shows superior optimization performance, particularly in F8, where its optimization ability surpasses that of other algorithms. For F9–F11, MISWO’s convergence speed and accuracy far exceed those of other algorithms. In F12–F13, MISWO achieves optimization results that are several orders of magnitude better than those of other algorithms, including the original. Moreover, compared to the original algorithm, MISWO demonstrates significant improvements in both convergence speed and optimization ability. For the fixed-dimensional multimodal functions, some graphs are enlarged for better analysis. In F14–F15, although MISWO performs slightly slower in terms of convergence speed, it still reliably finds the optimal solution with excellent precision. In F16, MISWO shows fast convergence while also obtaining the optimal value. For F17–F19, the differences among the algorithms are minimal. For F20–F23, MISWO’s convergence speed is only marginally slower than that of WOA. Overall, these observations validate the effectiveness of MISWO across various test functions, showcasing its superior convergence speed and optimization capability in most scenarios.

Figure 4
figure 4

The convergence curves for the F1-F23 test functions (Part 1).

Full size image
Figure 5
figure 5

The convergence curves for the F1-F23 test functions (Part 2).

Full size image
Figure 6
figure 6

The convergence curves for the F1-F23 test functions (Part 3).

Full size image

Analysis of cec test function results

To further evaluate the performance of the Multi-Strategy Improved Spider Wasp Optimization (MISWO), this section employs the CEC2022 function test set for analysis. The CEC2022 test set consists of 12 single-objective test functions with boundary constraints, including unimodal functions (F1), multimodal functions (F2–F5), mixed functions (F6–F8), and combination functions (F9–F12). The testing dimensions are 2D, 10D, and 20D. MISWO and various algorithms discussed in the previous section were independently run 30 times on the CEC2022 function test set. Tables 3, 4, and 5 present the results for algorithms operating in 2D, 10D, and 20D, including optimal, average, and worst values for each algorithm.

In the case of the unimodal function (F1), MISWO achieved optimal values across all testing dimensions of 2D, 10D, and 20D, with the optimal, average, and worst values being identical. For multimodal functions (F2–F5), MISWO attained optimal values under 2D conditions, where the optimal, average, and worst values were also the same. In 10D, MISWO secured optimal values in F2, F3, and F5, again with consistent optimal, average, and worst values. For F4, MISWO outperformed other algorithms by achieving the optimal value, with both average and worst values also being optimal. In 20D, MISWO exhibited superior performance compared to other algorithms.

For the mixed functions (F6–F8), MISWO consistently outperformed the other algorithms. Regarding the combination functions (F9–F12), except in the 20D case where the results for F10 were slightly inferior to those of CHIO, MISWO achieved the best results across the remaining dimensions.

Table 3 Cec2022 test results (dim = 2).
Full size table
Table 4 Cec2022 test results (dim = 10).
Full size table
Table 5 Cec2022 test results (dim = 20).
Full size table

Engineering optimization problems and analysis

Engineering problems are often characterized by complexity, involving numerous variables and constraints, which makes them difficult to solve. To demonstrate the effectiveness of the MISWO algorithm, several engineering optimization problems are selected for evaluation. These include the design of a tension/compression spring, pressure vessel, and welding beam-problems with fewer constraints and parameters. Additionally, more complex challenges such as speed reducer design, which includes multiple constraints, and automobile side-impact design are also examined. MISWO’s performance will be compared to that of several other algorithms, including the original SWO, in terms of both optimization results and convergence behavior. This comparison aims to thoroughly investigate MISWO’s stability and optimization capability in addressing complex engineering optimization problems.

Tension/compression spring design

The tension/compression spring design31, as depicted in Fig. 5, aims to minimize the mass while satisfying constraints such as minimum deflection, shear stress, oscillation frequency, and outer diameter limits. It involves three design variables: the wire diameter (d), the mean coil diameter (D), and the number of active coils (P). The mathematical model is as follows:

Figure 7
figure 7

Tension/compression spring design.

Full size image
$$\begin{aligned} \begin{aligned} \min f(x)=(P+2) D d^2 \\ \text{ s.t. } \quad g_1(x)=1-\frac{D^3 P}{71785 d^4} \le 0 \\ g_2(x)=\frac{4 D^2-d D}{12566\left( D d^3-d^4\right) }+\frac{1}{5108 d^2}-1 \le 0 \\ g_3(x)=1-\frac{140.45 d}{D^2 P} \le 0 \\ g_4(x)=\frac{D+d}{1.5}-1 \le 0 \end{aligned} \end{aligned}$$
(27)

The boundary constraint conditions are as follows:\(0.05 \le d \le 2\), \(0.25 \le D \le 1.3\), \(2 \le P \le 15\).The optimization results for each algorithm are shown in Table 6. The results indicate that MISWO outperforms other algorithms in the design of tension/compression springs. When d=0.0517652, D=0.3585528, P=11.1821947 the minimum mass of the spring is achieved at 0.0126653. Additionally, the convergence curves of MISWO and other algorithms in the design of tension/compression springs are shown in Fig. 6. From the convergence curves, it can be observed that MISWO not only obtains the optimal value but also converges faster compared to other algorithms.

Table 6 Tension/compression spring design.
Full size table
Figure 8
figure 8

Convergence curve of tension/compression spring design.

Full size image

Pressure vessel design

Pressure vessel design32 The objective, as shown in Figure 7, is to minimize costs while meeting production requirements. This includes 4 design variables: shell thickness (\(T_s\)),head thickness (\(T_h\)), inner radius of the container (R), and the length of the container excluding the head (L). The mathematical model is as follows:

Figure 9
figure 9

Pressure vessel design.

Full size image
$$\begin{aligned} \begin{aligned} \min f(x)=\left( 0.6224 T_s R L+1.7781 L T_s ^2\right. \\ +3.1661 R^2 T_h+19.84 R^2 T_s \\ \text{ S.t. } g_1(x)=-R+0.0193 T_s \le 0 \\ g_2(x)=-L+0.00954 T_s \le 0 \\ g_3(x)=-\pi L R^2-\frac{4}{3} R^3+1296000 \le 0 \\ g_4(x)=L-240 \le 0 \end{aligned} \end{aligned}$$
(28)

The boundary constraints are as follows:\(0.51 \le R \le 99.49\), \(0.51 \le L \le 99.49\), \(10 \le T_s \le 200\), \(10 \le T_sh \le 200\)The optimization results for each algorithm shown in Table 7. When \(T_s\)=13.4311960, \(T_h\)=6.8949393, R =42.0984455 L=176.6365958 MISWO is able to find the minimum value of 6059.714335. The results indicate that MISWO outperforms other algorithms in pressure vessel design optimization. Additionally, the convergence curves of MISWO and other algorithms in pressure vessel design are shown in Fig. 8. It is evident from the convergence curves that MISWO achieves better convergence speed and accuracy compared to other algorithms.

Table 7 Pressure vessel design.
Full size table
Figure 10
figure 10

Convergence curve of pressure vessel design.

Full size image

Cantilever beam

Cantilever beam33 shown in Fig. 9 is a structural engineering design problem related to the weight optimization of a cantilever beam with a square cross-section. One end of the cantilever beam is rigidly supported, and it is subjected to a vertical force at the free node of the cantilever. The cantilever beam consists of 5 hollow square blocks with constant thickness, where the height (or width) of the blocks is the decision variable, and the thickness is fixed. The mathematical formulation of this problem is as follows:

Figure 11
figure 11

Cantilever beam.

Full size image
$$\begin{aligned} \begin{aligned} \quad \min f(x)&=0.0624\left( h_1+h_2+h_3+h_4+h_5\right) \\ \text{ s.t. } \quad&g_1(x)=\frac{61}{h_1 ^3}+\frac{37}{h_2 ^3}+\frac{19}{h_3 ^3}+\frac{7}{h_4 ^3}+\frac{1}{h_5 ^3}-1 \le 0 \end{aligned} \end{aligned}$$
(29)

The boundary constraints are as follows:\(0.01 \le h_1 \le 100\), \(0.01 \le h_2 \le 100\), \(0.01 \le h_3 \le 100\), \(0.01 \le h_4 \le 100\),\(0.01 \le h_5 \le 100\) MISWO obtained the optimal solution for the cantilever beam design problem as shown in Table 8 when \(h_1\)=6.0132964, \(h_2\)=5.3091224, \(h_3\)=4.4981706,\(h_4\)=3.5019521,\(h_5\)=2.1511353 ,resulting in an optimal value of 1.3399574. Additionally, the convergence curves of MISWO and other algorithms for solving the cantilever beam design problem are depicted in Fig. 10. From the convergence curves, it is evident that MISWO not only achieves the optimal value but also converges faster than other algorithms.

Table 8 Cantilever beam.
Full size table
Figure 12
figure 12

Cantilever beam.

Full size image

Piston lever

As shown in Fig. 11, the main objective of the Piston Lever34is to minimize the oil volume when the piston rod moves from \(0^{\circ }\) to \(45^{\circ }\). This is achieved by arranging the piston components H B D X appropriately. The mathematical model for the piston lever design problem is as follows:

Figure 13
figure 13

Piston lever.

Full size image
$$\begin{aligned} \begin{aligned} \min f(x)=\frac{1}{4} \pi D^2\left( L_2-L_1\right) \\ \text{ S.t. } g_1(x)=Q L \cos \theta -R * F \le 0 \\ g_2(x)=Q(L-X)-M_{\max } \le 0 \\ g_3(x)=1.2\left( L_2-L_1\right) -L_1 \le 0 \\ g_4(x)=\frac{D}{2}-B \le 0 \end{aligned} \end{aligned}$$
(30)

The boundary constraints are as follows:

$$\begin{aligned} \begin{aligned} 0.05 \le H \le 500 \\ 0.05 \le B \le 500 \\ 0.05 \le X \le 500 \\ 0.05 \le D \le 200 \\ R=\frac{|-X(X \sin \theta +H)+H(B-X \cos \theta )|}{\sqrt{\left( X-B^2\right) +H^2}} \\ F=\frac{\pi P D^2}{4} \\ L_2=\sqrt{(X \sin \theta +H)^2+(B-X \cos \theta )^2} \\ \theta =45^{\circ } \\ Q=10000 l b s \\ L=240 \text{ in } \\ L_1 \\ M_{\max }=1.8 * 10^6 l b s \text{ in } \\ P=1500 \text{ psi } \end{aligned} \end{aligned}$$
(31)

Table 9 displays the optimization results for the Piston Lever design problem, where MISWO obtained the optimal solution compared to other algorithms. Additionally, the convergence curve in Figure 12 indicates that MISWO has excellent convergence speed and accuracy.

Table 9 Piston lever.
Full size table
Figure 14
figure 14

Convergence curve of piston lever.

Full size image

Speed reducer design

The primary objective of the Speed reducer design problem35 is to minimize its weight while satisfying 11 constraints. There are seven variables involvedb, gear modulemnumber of teeth on the pinio:z length of the first shaft between bearings \(l_1\) length of the second shaft between bearings \(l_2\)diameter of the first shaft \(d_1\) and diameter of the second shaft \(d_2\) As shown in Fig. 13, solving for these variables yields the weight of the speed reducer.

Figure 15
figure 15

Speed reducer design.

Full size image

The boundary constraints are as follows:

$$\begin{aligned} \begin{aligned} 2.6 \le b \le 3.6 \\ 0.7 \le m \le 0.8 \\ 17 \le z \le 28 \\ 7.3 \le l_1 \le 8.3 \\ 7.8 \le l_2 \le 8.3 \\ 2.9 \le d_1 \le 3.9 \\ 5.0 \le d_2 \le 5.5 \end{aligned} \end{aligned}$$
(32)

The mathematical model for the speed reducer design problem is as follows:

\(\begin{aligned} \min f(x)=&0.7854 b m^2\left( 3.3333 z^2+149334 z-43.0934\right) -1.508 b\left( d_1 ^2+d_2 ^2\right) +7.4777\left( d_1 ^3+d_2 ^3\right) \\ &+0.7854\left( l_1 d_1 ^2+l_2 d_2 ^2\right) \end{aligned}\)

$$\begin{aligned}&\begin{aligned}&\text{ s.t. } g_1(x)=\frac{27}{b m^2 z}-1 \le 0 \\&g_2(x)=\frac{397.5}{b m^2 z^2}-1 \le 0 \\&g_3(x)=\frac{1.93 l_1^3}{m d_1^2 z}-1 \le 0 \\&g_4(x)=\frac{1.93 l_2^3}{m d_2^2 z}-1 \le 0 \end{aligned}\nonumber \\&\begin{aligned} g_5(x)=\frac{\sqrt{\left( \frac{745 l_1}{m z}\right) ^2+16.9 * 10^6}}{110 d_1 ^3}-1 \le 0 \\ g_6(x)=\frac{\sqrt{\left( \frac{745 l_2}{m z}\right) ^2+157.5 * 10^6}}{85 d_2 ^3}-1 \le 0 \\ g_7(x)=\frac{m z}{40}-1 \le 0 \\ g_8(x)=\frac{5 m}{b}-1 \le 0 \\ g_9(x)=\frac{b}{12 m}-1 \le 0 \\ g_{10}(x)=\frac{1.5 d_1+1.9}{l_1}-1 \le 0 \\ g_{11}(x)=\frac{1.1 d_2+1.9}{l_2}-1 \le 0 \end{aligned} \end{aligned}$$
(33)

The speed reducer design problem was solved using various algorithms, and the values of each parameter are presented in Table 10. According to the data in the table, the minimum value of the problem was obtained by MISWO, and the values of the core parameters were optimized. This effectively reduced the cost of engineering design. Additionally, from the convergence curves of the algorithms shown in Fig. 14, it can be observed that MISWO exhibits superior convergence speed and accuracy compared to other algorithms, leading to improved optimization results.

Table 10 Speed reducer design.
Full size table
Figure 16
figure 16

Convergence curve of speed reducer design.

Full size image

Car side impact design

In consideration of the collision force and stress on the car, minimize the weight of the door using nine parameters36. The variables are the thickness of the B-pillar inner panel \(x_1\) Reinforcements for the B-pillar \(x_2\) Thickness of the floor inner side \(x_3\) Crossbeam \(x_4\) Door beam \(x_5\) Door beltline reinforcement \(x_6\) Roof longitudinal beam \(x_7\) B Inner side of the B-pillar \(x_8\) Inner side of the floor? \(x_9\) Guardrail height \(x_10\) Collision position \(x_11\). As shown in Fig.  15, the mathematical model for the car side collision design problem is as follows?

Figure 17
figure 17

Car side impact design.

Full size image
$$\begin{aligned} \begin{aligned}&\min f(x)=1.98+4.90 x_1+6.67 x_2+6.98 x_3+4.01 x_4+1.78 x_5+2.73 x_7 \\&\text{ S.t. } g_1(x)=1.16-0.3717 x_2 x_4-0.00931 x_2 x_{10}-0.484 x_3 x_9+0.01343 x_6 x_{10}-1 \le 0 \\&g_2(x)=46.36-9.9 x_2-12.9 x_1 x_2-0.1107 x_3 x_{10}-32 \le 0 \\&g_3(x)=33.86-9.9 x_2-2.95 x_3-0.1792 x_3-5.057 x_1 x_2-11.0 x_2 x_8-0.0215 x_5 x_{10}-9.98 x_7 x_8-22.0 x_8 x \\&-32 \le 0 \\&g_4(x)=28.98+3.818 x_3-4.2 x_1 x_2+0.0207 x_5 x_{10}+6.63 x_6 x_9-7.7 x_7 x_8+0.32 x_9 x_{10}-32 \le 0 \\&g_5(x)=0.261-0.0159 x_1 x_2-0.188 x_1 x_8-0.019 x_2 x_7+0.0144 x_3 x_5+0.0008757 x_5 x_{10}+0.08045 x_6 x_9 \\&+0.00139 x_8 x_{11}+0.00001575 x_{10} x_{11}-0.32 \le 0 \\&g_6(x)=0.214+0.00817 x_5-0.131 x_1 x_8-0.0704 x_1 x_9+0.03099 x_2 x_6-0.018 x_2 x_7+0.0208 x_3 x_8 \\&+0.121 x_3 x_9-0.00364 x_5 x_6+0.0007715 x_5 x_{10}-0.0005354 x_6 x_{10}+0.00121 x_8 x_{11} \\&+0.00184 x_9 x_{10}-0.02 x_2^2-0.32 \le 0 \\&g_7(x)=0.74-0.61 x_2-0.163 x_3 x_8+0.001232 x_3 x_{10}-0.166 x_7 x_9+0.227 x_2 ^2-0.32 \le 0 \\&g_8(x)=4.72-0.5 x_4-0.19 x_2 x_3-0.0122 x_4 x_{10}++0.009325 x_6 x_{10}+0.000191 x_{11}^2-4 \le 0 \\&g_9(x)=10.58-0.674 x_1 x_2-1.95 x_2 x_8+0.02054 x_3 x_{10}-0.0198 x_4 x_{10}+0.028 x_6 x_{10}-9.9 \le 0 \\&g_{10}(x)=16.45-0.489 x_3 x_7-0.843 x_5 x_6+0.0432 x_9 x_{10}-0.0556 x_9 x_{11}-0.000786 x_{11}^2-25.7 \le 0 \\ \end{aligned} \end{aligned}$$
(34)

The boundary constraints are as follows:

$$\begin{aligned} \begin{aligned}&0.5 \le x_1, x_2, x_3, x_4, x_5, x_6, x_7 \le 1.5\\&\begin{aligned} 0&\le x_{8,} x_9 \le 1 \\ -30&\le x_{10}, x_{11} \le 30 \end{aligned} \end{aligned} \end{aligned}$$
(35)

The optimization results for the car side collision design problem, obtained through various algorithms for 11 variables, are presented in Table 11. From the data in the table, it is evident that MISWO consistently provides the optimal solution compared to other algorithms when faced with multi-parameter engineering problems involving 11 variables. This demonstrates that MISWO exhibits excellent adaptability and robustness in solving multi-constraint, multi-variable engineering problems. An analysis of the convergence curves of MISWO and other algorithms, as shown in Fig. 16, reveals that MISWO converges faster towards the optimal solution in the early stages and achieves the optimal solution ahead of other algorithms as the number of iterations increases. This indicates that MISWO excels in both optimization capability and convergence speed.

Table 11 Car side impact design.
Full size table
Figure 18
figure 18

Convergence curve of car side impact design.

Full size image

UAV trajectory planning

Unmanned Aerial Vehicle (UAV) is an unmanned aircraft controlled by radio remote control equipment and self-contained program control devices. It can operate remotely or autonomously, allowing ground personnel to pre-program, monitor, and control it.With the rapid development of UAV technology, the application scenarios and flight environments of UAVs are becoming increasingly diverse and complex. Particularly in harsh and uncertain conditions, UAV flights may face severe challenges from various obstacles and potential threats. Enhancing UAV autonomy and reducing human intervention are crucial goals, and UAV flight path planning is a key means to achieve these objectives. UAV trajectory planning aims to navigate from a designated starting point to a target area within specific mission terrain and environment, following constraints such as flight speed, altitude, range, and time, while avoiding restricted zones like bad weather areas, radar threat zones, and no-fly zones. When performing flight missions, UAVs navigate from a predetermined starting point through complex mountainous environments to reach designated task points. During the flight, they encounter various threats, including mountain collisions and weather-related hazards. Effective modeling of the environment and terrain is fundamental to improving path planning efficiency. First, the basic reference terrain is modeled. The model for the reference terrain is as Eq.36:

$$\begin{aligned} \begin{aligned}&Z_{1(x, y)}=\sin (y+a)+b \cdot \sin (x)+ \\&c \cdot \cos \left( d \cdot \sqrt{x^2+y^2}\right) +e \cdot \cos (y)+ \\&\quad f \cdot \sin \left( f \cdot \left( x^2+y^2\right) \right) +g \cdot \cos (y) \end{aligned} \end{aligned}$$
(36)

In the formula,\(Z_{1(x, y)}\)represents the height value corresponding to a point on the horizontal plane, where x and y are the coordinates of the projected point on the horizontal plane.The parameters a,b,c,d,e,f and gcontrol the undulations of the reference terrain in the established map. The natural mountainous terrain encountered during flight missions is represented by the following Eq.37:

$$\begin{aligned} Z_{2(x, y)}=\sum _{i=1}^n h_i \exp \left[ -\left( \frac{x-x_i}{x_{s i}}\right) ^2-\left( \frac{y-y_i}{y_{s i}}\right) ^2\right] +h_0 \end{aligned}$$
(37)

Flight altitude constraint:

$$\begin{aligned} L \le i \le H \end{aligned}$$
(38)

L represents the lower limit of flight altitude, H represents the upper limit of flight altitude. Drones are not allowed to expand with obstacles.The obstacle area is \(O_i\)(i is the obstacle number), and (x, y, z) represents the position of the drone.

$$\begin{aligned} (x, y, z) \notin O_i \quad \forall i \end{aligned}$$
(39)

Drones are subject to speed constraints during flight.\(v_{\max }\) represents the maximum speed, \(v_{\min }\) represents the minimum speed, and \(\dot{\textbf{p}}=(\dot{x}, \dot{y}, \dot{z})\) represents the velocity vector of the drone. The mathematical formula for the speed constraint of unmanned aerial vehicles is as follows.

$$\begin{aligned} v_{\min } \le \Vert \dot{\textbf{p}}\Vert \le v_{\max } \end{aligned}$$
(40)

The flight time of drones is constrained by the energy they carry, and can be approximated by limiting the total length or total time of the flight path.Assuming the maximum flight time of the drone is \(T_{\max }\), the actual flight time is T, and \(v_{\text{ avg } }\) represents the average speed. Obtain the endurance constraint equation.

$$\begin{aligned} \int _0^T\Vert \dot{\textbf{p}}(t)\Vert d t \le v_{\textrm{avg}} \cdot T_{\max } \end{aligned}$$
(41)

The flight of drones is also limited by their dynamic characteristics, such as maximum turning angular velocity, maximum acceleration, etc. These constraints typically involve more complex dynamic equations, such as:

$$\begin{aligned} \left\| \frac{d \dot{\textbf{p}}}{d t}\right\| \le a_{\max } \end{aligned}$$
(42)

\(\varvec{a}_{\max }\) is the maximum acceleration. The result of using MISWO to solve this problem is shown in Fig. 17, and the convergence curve is shown in Fig. 18.

In summary, the proposed MISWO algorithm demonstrates superior performance when tackling various real-world engineering problems of different complexities. Through comparisons with other algorithms and handling of different parameters, MISWO consistently outperforms the original SWO algorithm as well as several state-of-the-art and widely referenced optimization algorithms in terms of cost efficiency for solving practical engineering problems. This highlights MISWO’s excellent solving capability, convergence speed, stability, and practicality when addressing real-world optimization challenges (Figs. 19, 20).

Figure 19
figure 19

UAV trajectory planning.

Full size image
Figure 20
figure 20

Convergence curve UAV trajectory planning.

Full size image

Conclusion

The paper proposes an improved Spider Wasp Optimization (MISWO) algorithm utilizing a hybrid strategy to enhance global optimization performance. In the initialization phase, the Grey Wolf Optimizer (GWO) is integrated to boost the algorithm’s convergence rate and improve the initial population’s fitness, resulting in better early-stage performance. During the search phase, an adaptive step size operator is employed to dynamically adjust the spider wasp’s search range, improving optimization precision and aiding in escaping local optima. Additionally, a dynamic trade-off rate (TR) is introduced to further optimize performance. A dynamic lens imaging reverse learning strategy is also used to generate reverse solutions, update optimal individuals, and prevent the algorithm from stagnating in local optima. A greedy strategy is applied to select the best individuals, enhancing the algorithm’s ability to escape local traps and accelerate convergence.

The MISWO algorithm is tested on 23 complex benchmark functions with various characteristics, and its convergence behavior is analyzed. The Modified Evolutionary Optimization (MEO) algorithm is then applied to eight complex engineering design problems, comparing MISWO’s performance against the original SWO and several state-of-the-art optimization algorithms. Experimental results demonstrate that MISWO possesses strong optimization capabilities and holds significant practical value in solving real-world challenges.

However, the current research has limitations. MISWO’s performance in large-scale and more complex engineering scenarios, especially multi-objective engineering optimization problems, requires further improvement. Future research will focus on refining MISWO, expanding its application to more diverse engineering fields, and conducting more realistic simulations.