Introduction

Building a ship involves several critical stages1,2, including hull construction, painting, and outfitting. Among these, hull construction is a key phase in modern shipbuilding technology. It is a highly customized, long-cycle production process that requires the coordination of extensive resources and personnel, making effective management a significant challenge. Efficient production scheduling not only enhances resource utilization but also shortens the production cycle. Under modern shipbuilding models, hull construction is divided into various blocks to be manufactured separately and then assembled step by step. Obviously, the production efficiency of these blocks directly impacts the overall shipbuilding cycle. Among all block types, plane blocks constitute the largest proportion, making them critical to the shipbuilding process. These blocks are characterized by their high quantity, diversity, and stringent quality requirements. They must be manufactured in strict accordance with the specifications established during the ship design phase, as they serve as the fundamental units that define the ship’s main dimensions. These dimensions are closely related to the ship’s operability, seaworthiness, and ice resistance capabilities3,4. The manufacturing process of plane blocks is crucial to the entire shipbuilding lifecycle, and the efficiency of their production directly affects the overall efficiency of a shipbuilding enterprise. Therefore, the production scheduling management of the plane block manufacturing procedure is of great significance.

The ship plane block is manufactured by assembling various spare parts, including the longitudinal bone, T beam, and Frame. These spare parts are fabricated simultaneously with the assembly process. Hence, the production management of plane blocks effectively becomes the scheduling optimization of block assembly processes. Although there exist lots of methods aiming to optimize the schedules of assembling flow lines, they are unsuitable for ship plane block assembly for several reasons as follows.

Existing research on flow line scheduling can be broadly categorized into two areas: one focusing on the structure of the flow line and the other on resource allocation, including workers, machines, and tools, while taking into account the flow line’s structural characteristics. Unlike these renewable resources, which are released after assembly task completion, spare parts in ship plane block assembly are non-renewable and cannot be reused. Most studies presume that spare parts are prefabricated and readily available, thereby concentrating solely on the assembly process. However, in ship plane block flow lines, spare parts fabrication and assembly occur within the same workshop. Spare parts are produced and then assembled sequentially, without bulk storage, resulting in restricted buffer space. An inadequate supply of spare parts can starve assembly stations, while an overflow buffer can block production. Consequently, spare parts availability becomes a critical constraint in plane block assembly. Additionally, plane block manufacturing is labor-intensive and depends heavily on the availability of work teams with specific skills and varying proficiency levels. Worker teams can only be assigned to workstations when they are available and possess the required skills. Even among workers with the same skills, differences in proficiency can affect efficiency. Because the number of worker teams is limited, labor resources present a second significant constraint in plane block assembly. These constraints add considerable complexity to the scheduling of ship plane block flow lines.

Based on the above analysis, solving the scheduling optimization problem for ship plane block flow lines requires simultaneously addressing task allocation for multiple work teams, spare parts supply, and block assembly sequence optimization. This multifaceted requirement adds complexity beyond traditional scheduling problems, which usually address either renewable resource constraints or task sequencing in isolation. Therefore, the ship plane block scheduling optimization problem is defined as a dual-resource-constrained block flow shop scheduling problem (DRCBFSP), where both work teams and spare parts supply are integrated into the solution framework. To the best of our knowledge, no existing literature addresses this specific combination of dual resource constraints in ship plane block manufacturing, highlighting the novelty of this work. The contributions of this paper are threefold:

  1. 1.

    The paper establishes a comprehensive mathematical model to capture the unique constraints of DRCBFSP.

  2. 2.

    A novel meta-heuristic algorithm, an improved Grey Wolf Optimization (IGWO), is proposed to solve the problem effectively.

  3. 3.

    The model and algorithm are validated through extensive experimental results, demonstrating significant improvements in scheduling performance and production efficiency in realistic ship plane block flow line scenarios. These contributions advance the field by addressing a practical and complex issue that has not been previously explored.

The remainder of this paper is organized as follows. Section “Related work” reviews related work, section “3” describes the problem and develops the model, section “The IGWO algorithm for solving the DRCBFSP” outlines the proposed solution approach, section “Experimental study” presents experimental results, and section “Conclusions and future research” concludes with future research directions.

Related work

Since Johnson introduced the flow shop scheduling problem (FSP) in 1954, it has been extensively studied by scholars5. As production processes and job environments in actual workshops have grown increasingly complex, numerous extensions of the classic FSP have garnered significant attention, such as the Flexible Flow Shop scheduling problem6, the Blocking Flow Shop scheduling problem7, the Permutation Flow Shop scheduling problem8, and the Distributed Flow Shop scheduling problem9. Given the large volume and weight of ship plane blocks, as well as the lack of buffer zones between workstations in the flow line, the ship plane block scheduling problem can be classified as a block flow shop problem (BFSP) based on the flow line’s structure. Wang et al.10 developed a nonlinear integer programming model and introduced rescheduling methods to minimize early and delayed delivery costs in hybrid flow line scheduling for shipbuilding panel blocks. Additionally, a comprehensive review of BFSP research conducted before 2019 is available in reference11. Since 2019, scholars have continued to explore this topic. For example, Qin et al.12 proposed a mathematical model for the blocking hybrid flow line workshop scheduling problem, addressing energy consumption, and developed an effective IGS algorithm to solve it. Guo et al.13 addressed blockages in plane block flow lines, aiming to minimize makespan, carbon emissions, and noise costs associated with ship blocks. Cheng et al.14 tackled blocking flow shop scheduling problems with sequence-dependent setup times using the Extended Iterative Greedy algorithm, demonstrating the superiority of their proposed algorithm. However, these studies do not account for the constraints posed by other external resources in optimizing flow line scheduling.

In various industries, Yang et al.15 required for events are crucial, as all resources are finite. The literature reviews the application of work-stealing techniques in the field of computer science to achieve load balancing across multi-processor resources, thereby optimizing computational power. Additionally, resource scheduling is a key research area in Network Function Virtualization (NFV) for 6G. Sun et al.16. proposed an efficient online service function chain deployment (OSFCD) algorithm that selects deployment paths based on proximity to the Service Function Chain (SFC) length. In real-world production scenarios, resources such as workers must be simultaneously considered to enhance overall productivity and performance17. Given the critical role of workers in production and constraints such as skills, availability, and preferences, efficient allocation of workers to each workstation can significantly boost workshop efficiency. Historically, the importance of worker allocation in assembly lines has attracted significant attention in production management. Winch et al.18 introduced the concept of matching workers with the required skills for tasks in assembly lines, aiming to minimize workforce size and laying the foundation for future research. In recent years, studies have continued to focus on the dynamics of worker allocation, particularly in flexible manufacturing systems. Lucia et al.19 examined job rotation among aging workers, emphasizing the need to optimize task-worker matching and reduce ergonomic loads. Behnamian20 proposed a hybrid competitive algorithm for mixed-flow operations with multiple worker allocations, noting that processing times depend on the number of workers assigned but did not account for variations in workers’ skills and production efficiencies. Liu et al.21 considered the multi-skilling of workers to address scheduling issues in mixed-flow assembly lines for complex products. Yang et al.22 proposed a filtered constraint search algorithm to optimize worker allocation and balance on automotive parts assembly lines, taking worker efficiency into account. Currently, research on allocation problems that consider worker mobility is limited in the existing literature. Wang et al.23 focused on aircraft final assembly workshops, optimizing worker allocation and mobility plans to minimize assembly cycles, balance work times, and reduce worker movement distances. Sikora et al.24 developed a mixed-integer linear programming model for the assembly line balancing problem, considering the transfer times of tasks and workers between workstations. However, the premise of the above research is that the workshop’s manufacturing plan is predetermined, and process scheduling and worker allocation are not simultaneously considered.

Since 2010, research on the integration of worker allocation and job process scheduling in workshop scheduling problems has experienced considerable growth. Caricato et al.25 explored the influence of workforce management on machine scheduling in manufacturing systems. They demonstrated that workforce availability and skills have a direct impact on machine schedules and propose a framework that integrates workforce planning into machine scheduling models to enhance overall system performance. Agnetis et al.26 addressed the workshop scheduling problem in handicraft production by assigning each task to a specific machine and operator. They proposed two heuristic algorithms using different decomposition strategies to optimize the sequence of each task. Gong et al.27 presented a hybrid evolutionary algorithm to tackle the flexible flow shop scheduling problem by jointly considering machine characteristics, worker skills, energy consumption, and worker-related costs. Marichelvam et al.28 investigated the mixed flow shop scheduling problem influenced by human factors, proposing an improved particle swarm optimization algorithm, which was validated through case studies involving automotive manufacturing units and a set of stochastic benchmark problems. Costa et al.29 introduced a discrete backtracking search algorithm to address the mixed flow line scheduling problem, where worker numbers are fewer than machines, aiming to minimize maximum completion time through optimal task and worker allocation. Liu et al.30 focused on the hybrid flow shop scheduling problem, incorporating multi-skilled workers and their fatigue factors. They employed agent-based simulation and optimization to simulate fatigue dynamics over time and dynamically adjust assignments to balance productivity and worker health. Han et al.31 explored hybrid flow shop scheduling, where worker constraints play a critical role in the scheduling process. They introduced a multi-objective evolutionary algorithm that incorporates heuristic decoding to optimize scheduling and worker assignment, effectively balancing objectives like minimizing makespan and labour utilization. Benavides et al.32 explored flow shop scheduling with heterogeneous workers, whose varying skills and proficiencies influence task allocation. Their model accounts for worker heterogeneity and enhances efficiency by assigning tasks according to workers’ abilities. Liu et al.33 analysed the dual challenge of scheduling and assigning multi-skilled workers in hybrid flow shops, proposing a bi-objective optimization approach that jointly optimizes the scheduling sequence and worker assignments, thereby enhancing efficiency and productivity. Zheng and Wang34 investigated the allocation of processing workers, solving the flexible job shop scheduling problem with an improved fruit fly optimization algorithm to minimize the maximum completion time. Méndez et al.35 examined the non-blocking flow line scheduling problem with a constrained discrete resource supply, addressing allocation, sorting, and renewable resources like electricity, workforce, and steam. Cheng et al.36 reformulated the development project relocation problem as a scheduling problem for a resource-constrained two-machine flow line, considering multiple resource types of consumption and recovery, and designed a polynomial algorithm to resolve it.

Metaheuristic algorithms have demonstrated significant success across various fields, as documented in existing literature. They have been applied effectively to optimize truss structures37,38, tune parameters of deep learning models39,40,41, and solve complex scheduling problems42,43,44.The Grey Wolf Optimization (GWO) algorithm is a swarm intelligence method that simulates the hunting behaviour of wolves. Its simplicity, minimal control parameters, and ease of implementation have led to extensive study and wide application. However, based on the above literature analysis and the comparison with representative studies in Table 1, existing research rarely addresses the hybrid problem of scheduling worker allocation and job processes under dual constraints. These constraints involve factors such as worker availability, skills, proficiencies, and non-renewable resource considerations, making current methods unsuitable for tackling the DRCBFSP encountered in ship plane block building. Therefore, this paper employs the improved Grey Wolf Optimizer (IGWO) to solve the DRCBFSP, highlighting its extraordinary significance.

Table 1 Comparison of this paper with the representative studies problem.
Full size table

Problem description and model building

Problem description and expression

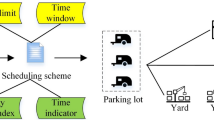
The DRCBFSP in ship plane block manufacturing, as illustrated in Fig. 1, is described as follows: There are N plane blocks \(I=\left\{ {1,2, \ldots ,i, \ldots ,N} \right\}\) that need to be assembled across M stations \(W=\left\{ {1,2, \ldots ,j \ldots ,M} \right\}\) in a block flow line, utilizing T work teams \(P=\left\{ {1,2, \ldots ,p, \ldots ,T} \right\}\). Each work team possesses varying skill levels, and their compatibility with machines and working efficiencies differ. The types and quantities of spare parts required for each block vary, with the required spare parts represented by \(R=\left\{ {1,2, \ldots ,r \ldots ,{\text{O}}} \right\},\) sourced from a buffer. The production efficiency of each spare part type is \(F=\left\{ {{F_1},{F_2}, \ldots ,{F_r} \ldots ,{F_O}} \right\}\), and the buffer capacity for storing each type of spare part is \(B=\left\{ {{B_1},{B_2}, \ldots ,{B_r} \ldots ,{B_O}} \right\}\).

Given that the production efficiency of spare parts is relatively stable and assumed to be a known constant, this paper adopts a “first fabricated, first assembled” approach. It focuses on the differences in production efficiency and buffer capacity for various spare part types, without addressing the workshop scheduling for spare part fabrication. The primary aim is to optimize task allocation among multiple work teams, manage the resource supply of spare parts, and determine the block assembly sequence to minimize the overall completion time for ship plane block assembly. The problem is characterized by the following constraints:

  • Spare Parts Constraint: Spare parts are fabricated simultaneously with the assembly process, and buffer storage is limited. Assembly at any station can only commence once the required spare parts are delivered to the assembly section.

  • Work Teams Constraint: Work teams must be assigned efficiently to tasks during assembly. Given their varying efficiencies and skill levels, it is critical to allocate tasks in a way that maximizes productivity.

Fig. 1
figure 1

Illustration of the DRCBFSP in the ship plane block manufacturing.

Full size image

Problem assumptions

To clarify the proposed problem, the following assumptions are considered:

  1. 1.

    Plane blocks cannot be interrupted once assembly has begun.

  2. 2.

    Each plane block can complete its assembly at the station and be stored there until the next station becomes available.

  3. 3.

    The transportation time from the buffer to the flow line is negligible.

  4. 4.

    Each plane block procedure can only be assembled at a unique station.

  5. 5.

    All stations and work teams are available at time 0.

  6. 6.

    Work teams cannot be interrupted during assembly process.

  7. 7.

    Stations can only be processed by one work team at a time.

  8. 8.

    The moving time of plane blocks between stations is not considered.

Model building

Based on the above problem description and assumption, the DRCBFSP described in this paper is established as a MILP model. The notations needed in the MILP model are listed as Table 2:

Table 2 Notations of the proposed DRCBFSP.
Full size table

In this paper, the objective function aims to minimize the maximum completion time for the entire assembly process. The mathematical representation of this objective is provided in Eq. (1):

$$\hbox{min} f=\hbox{max} \{ A_{{Me}}^{L}\} ,e \in E$$
(1)

The PFSP constraints are defined as follows: Eq. (2) limits assembly to one block per assembly event ___location. Equation (3) ensures each block is assigned to a single assembly event ___location. Equation (4) connects the start and end times of station assembly events. Equation (5) requires that assembly events at a station can start only after the completion of events at a preceding station and the occurrence of the preceding assembly event at the subsequent station. Equation (6) mandates that assembly events can move to the next station only after completion at the current station and availability of the subsequent station. Equation (7) represents the absence of blockage in the first assembly event, while Eq. (8) represents the absence of blockage in the last assembly workstation. Equations (9) and (10) establish the connection between the completion assembly time of assembly event locations and assembly operations on the station.

$$\sum\limits_{{i \in I}} {{y_{ie}}} \leqslant 1,\forall e \in E$$
(2)
$$\sum\limits_{{e \in E}} {{y_{ie}}} =1,\forall i \in I$$
(3)
$$A_{{je}}^{S}+\sum\limits_{{i \in I}} {(T_{{ij}}^{A} \cdot {y_{ie}})} =A_{{je}}^{E},\forall j \in J,e \in E$$
(4)
$$\hbox{max} (A_{{j - 1,e}}^{E},A_{{j,e - 1}}^{L})=A_{{je}}^{S},\forall 1<j \leqslant M,1<e \leqslant N$$
(5)
$$\hbox{max} (A_{{je}}^{E},A_{{j+1,e - 1}}^{L})=A_{{j,e}}^{L},\forall 1<j<M,1<e \leqslant N$$
(6)
$$A_{{j,1}}^{E}=A_{{j,1}}^{L},j \in J$$
(7)
$$A_{{M,e}}^{E}=A_{{M,e}}^{L},e \in E$$
(8)
$$C_{{ij}}^{S} \leqslant A_{{je}}^{S}+\varphi \cdot (1 - {y_{ie}}),\forall i \in I,j \in J,e \in E$$
(9)
$$C_{{ij}}^{S} \geqslant A_{{je}}^{S}+\varphi \cdot (1 - {y_{ie}}),\forall i \in I,j \in J,e \in E$$
(10)

The spare parts constraints are defined as follows: Eqs. (11) and (12) limit that spare parts of the same type must be assembled on the identical station. Equation (13) specifies that the reserve of any spare part at time \(\:t=0\) is zero. Equations (14) and (15) indicate that the quantity of spare parts stored in the buffer is related to the production, consumption, and buffer capacity of the spare parts.

$$\sum\limits_{{j \in J}} {{a_{rj}}} =1,r \in R$$
(11)
$$\sum\limits_{{r \in R}} {{a_{rj}}} =1,j \in J$$
(12)
$${B_{r,1,1}}=0,r \in R$$
(13)
$${B_{r,1,j}}=\hbox{min} ({F_r} \cdot {C_{1,j}},{B_r}),j>1$$
(14)
$${B_{r,i,j}}=\hbox{min} ({F_r} \cdot {C_{i,j}} - \sum\limits_{{i=1}}^{e} {\sum\limits_{{j=1}}^{M} {{a_{rj}} \cdot } {A_{rij}}} ,{B_r}),i>1,j>1,{y_{ie}}=1$$
(15)

The work teams constraints are defined as follows: Eq. (16) Ensures that each block is assembled by only one work team at any given workstation. Equation (17) enforces a precedence constraint, which mandates that any subsequent assembly event assigned to a work team can only start after the completion of the preceding event, maintaining a logical sequence of operations. Equation (18) specifies that the actual assembly duration of each section is determined by the availability of spare parts and the efficiency of the assigned work team. Equations (19) and (20) establish the connection between the completion times of the work team’s operations at event locations and the related assembly operations on the station.

$$\sum\limits_{{p \in P}} {{w_{ijp}}} =1,\forall i \in I,j \in J$$
(16)
$${x_{ijlp}} \geqslant {x_{ij,l+1,p}},\forall i \in I,j \in J,l<{H_P},p \in P,{w_{ijp}}=1$$
(17)
$$T_{{ij}}^{A}=\hbox{max} \left( {({A_{rij}} - {B_{rij}})/{E_r},0} \right)+\sum\limits_{{p \in P}} {{w_{ijp}} \cdot {\chi _{jp}} \cdot T_{{ij}}^{B}} ,i \in I,j \in J,r \in R$$
(18)
$$C_{{ij}}^{S} \leqslant D_{{lp}}^{S}+\varphi \cdot (1 - {x_{ijlp}}),\forall i \in I,j \in J,l \in L,p \in P,{w_{ijp}}=1$$
(19)
$$C_{{ij}}^{S} \geqslant D_{{lp}}^{S}+\varphi \cdot (1 - {x_{ijlp}}),\forall i \in I,j \in J,l \in L,p \in P,{w_{ijp}}=1$$
(20)

The IGWO algorithm for solving the DRCBFSP

Grey Wolf optimization Algorithm

The BFSP is classified as NP-hard45, making it computationally challenging to solve, especially as problem size increases such complexities. Metaheuristic algorithms like the GWO algorithm are highly effective due to their strong convergence properties, minimal parameter requirements, and ease of implementation. In the search and hunting process of the GWO algorithm, the alpha (α), beta (β), and delta (δ) wolves guide the omega (ω) wolves forward.

When the wolves discover the prey \({{\varvec{X}}_{\varvec{P}}}\), the following equations are used to simulate the process of surrounding the prey.

$${\mathbf{D}}=\left| {{\mathbf{C}} \cdot {{\mathbf{X}}_{\mathbf{P}}}(t) - {\mathbf{X}}(t)} \right|$$
(21)
$${\mathbf{X}}(t+1)={{\mathbf{X}}_{\mathbf{p}}}(t) - {\mathbf{A}} \cdot {\mathbf{D}}$$
(22)

\({\varvec{X}}\left( t \right)\) represents the position vector of the grey wolf in the iteration of t. \({\varvec{A}}\) and \({\varvec{C}}\) are coefficient vectors, which are represented by the following equations:

$${\mathbf{A}}=2{\mathbf{a}} \cdot {{\mathbf{r}}_{\mathbf{1}}} - {\mathbf{a}}$$
(23)
$${\mathbf{C}}=2{{\mathbf{r}}_{\mathbf{2}}}$$
(24)

\({{\varvec{r}}_1}\) and \({{\varvec{r}}_2}\) are random vectors in the interval from 0 to 1, and vector \({\varvec{a}}\) linearly decreases from 2 to 0 throughout the entire iteration cycle, which is represented by the following equation:

$${\mathbf{a}}=2 - 2(t/{{\text{T}}_{{\text{max}}}})$$
(25)

Therefore, based on the searching and hunting characteristics of the grey wolf, mathematical simulations of the processes are carried out by the Eqs. (26)–(28).

$$ {\mathbf{D}}_{{\mathbf{\alpha }}} = \left| {{\mathbf{C}}_{1} \cdot {\mathbf{X}}_{{\mathbf{\alpha }}} - {\mathbf{X}}} \right|,\;{\mathbf{D}}_{{\mathbf{\beta }}} = \left| {{\mathbf{C}}_{{\mathbf{2}}} \cdot {\mathbf{X}}_{{\mathbf{\beta }}} - {\mathbf{X}}} \right|,\;{\mathbf{D}}_{{\mathbf{\delta }}} = \left| {{\mathbf{C}}_{{\mathbf{3}}} \cdot {\mathbf{X}}_{{\mathbf{\delta }}} - {\mathbf{X}}} \right| $$
(26)
$$ {\mathbf{X}}_{{\mathbf{1}}} = {\mathbf{X}}_{{\mathbf{\alpha }}} - {\mathbf{A}}_{{\mathbf{1}}} \cdot {\mathbf{D}}_{{\mathbf{\alpha }}} ,\;{\mathbf{X}}_{{\mathbf{2}}} = {\mathbf{X}}_{{\mathbf{\beta }}} - {\mathbf{{\rm A}}}_{{\mathbf{2}}} \cdot {\mathbf{D}}_{{\mathbf{\beta }}} ,\;{\mathbf{X}}_{{\mathbf{3}}} = {\mathbf{X}}_{{\mathbf{\delta }}} - {\mathbf{A}}_{{\mathbf{3}}} \cdot {\mathbf{D}}_{{\mathbf{\delta }}} $$
(27)
$${\mathbf{X}}=({{\mathbf{X}}_{\mathbf{1}}}+{{\mathbf{X}}_{\mathbf{2}}}+{{\mathbf{X}}_{\mathbf{3}}})/3$$
(28)

The IGWO Algorithm for the DRCBFSP

The effectiveness of the GWO algorithm in addressing the BFSP, particularly when enhanced with the Ranked Order Value (ROV) method and a Variable Neighbourhood Search strategy, has been demonstrated in prior research13. These methods address the discrete nature of the problem while improving local search precision. Building on the ROV method’s mapping rules, this paper develops novel solution methods tailored to the unique characteristics of the DRCBFSP, focusing on task allocation, spare part resource supply, and the optimization of the block assembly sequence. Given that the DRCBFSP is NP-hard and prone to local optima, the basic GWO algorithm alone may not be sufficient. To improve solution quality, we incorporate several enhancements. First, we generate part of the initial population using the NEH heuristic method, combined with reverse learning to diversify the initial solutions. Additionally, we introduce nonlinear search factors, dynamic inertia weight adjustments, and Gaussian mutation perturbation strategies to enhance the exploration capabilities and avoid local optima during the optimization process.

Encoding and decoding

This paper aims to optimize the blocks assembly sequences and the task allocation of work teams. Therefore, each grey wolf is represented by two vectors: \(BSV\) (Block Assembly Sequence) and \(WAV\) (Work Team Assignment Sequence).

The vector \(BSV\) represents the blocks assembly sequence and uses a complete arrangement encoding method. The length of the \(BSV\) vector is equal to the number of blocks, N. For example, the vector \(BSV=\left\{ {1,3,2, \ldots 9,7,5} \right\}\) indicates that block 1 is the first to be assembled, block 3 is the second, and so on.

The vector \(WAV\) represents the allocation of work teams to each block at the stations along the flow line. The vector \(WAV=\left\{ {U{J_1},U{J_2}, \ldots U{J_i} \ldots U{J_N}} \right\}\) is divided into N sub-parts and each sub-part can be represented as \(W{J_i}=\left\{ {{u_{i1}},{u_{i2}}, \ldots {u_{ij}} \ldots {u_{iM}}} \right\}\). The length of each sub-part equals the number of stations and the \({u_{ij}}\) in the sub-part represents the work team assigned to the \(i~th\) block on the \(j~th\) station. The initial vector \(WAV\) is randomly generated by selecting work teams from the P set. A specific example is shown in Fig. 2.

Fig. 2
figure 2

Encoding and decoding example.

Full size image

The basic GWO is commonly used to solve optimization problems for continuous variable functions, while the DRCBFSP is a discrete problem. Therefore, the ROV rule was used to transform the discrete scheduling solution into a continuous individual position vector. For each position vector of the grey wolf individual, an element is generated and arranged in ascending order. Each element corresponds to an ROV value, which represents the process arrangement scheme corresponding to the position vector, as shown in Fig. 3a.

Similarly, it is necessary to transform the scheduling scheme of blocks into the position vector of individual grey wolves using the ROV rule. Firstly, \(\:n\) random numbers are generated in the range of [0,\(\:n\)] (where \(\:n\) is the number of blocks). Secondly, an ROV value is assigned to each grey wolf position element according to the ascending rule, corresponding to the block scheduling scheme. Lastly, the values of each element in the grey wolf individual position vector are determined by the ROV rule. The conversion process is shown in Fig. 3b.

Fig. 3
figure 3

The ROV rule.

Full size image

Population initialization

When initializing the \(\:BSV\) vector, this paper employs two methods to improve the quality and diversity of the initial population. A portion of the initial populations is generated based on the NEH heuristic method, while the others are generated using a random process, as shown in Eq. (29). Additionally, this paper utilizes the reverse learning strategy, as shown in Eq. (30).

$${X_{i,j}}=lowe{r_j}+(uppe{r_j} - lowe{r_j}) \cdot random,i=(1,2,\ldots p),j=(1,2,\ldots n)$$
(29)
$${\hat {X}_{i,j}}=(uppe{r_j}+lowe{r_j}) - {X_{i,j}},i=(1,2,\ldots p),j=(1,2,\ldots n)$$
(30)

The WAV vector is initialized randomly by allocating work teams to each block operation. After initializing the \(\:BSV\) and \(\:WAV\) vectors, the initial and reverse populations are merged, and the fitness function is evaluated for each individual in the population. Finally, the top \(\:N\) optimal solutions are then selected as the new initial population of grey wolves.

Individual position update

Each grey wolf updates its \(\:BSV\) and \(\:WAV\) vectors during the position update stage. To improve the search capability and avoid the basic GWO algorithm’s tendency to get stuck in local optima, several enhancements are applied. In the basic GWO search strategy, the \(\:A\) vector determines whether grey wolf individuals expand the global search range or perform local search optimization. The vector \(\:a\) is an essential factor of the \(\:A\) vector. This paper transforms the vector \(\:a\) from linearly decreasing to exponentially decreasing to improve the early global search ability. Moreover, this paper introduces a dynamic inertia weight factor to improve the searchability of candidate grey wolf individuals to jump out of local optimal solutions. At the same time, this paper introduces a Gaussian mutation perturbation strategy to avoid situations where local optima cannot be escaped promptly during the iteration process. The calculations are represented by Eqs. (31)–(34).

$${\mathbf{D}}=\left| {{\mathbf{C}} \cdot {{\mathbf{X}}_{\mathbf{P}}}(t) - \omega \cdot {\mathbf{X}}(t)} \right|$$
(31)
$${\mathbf{a}}{\text{=}}2 \cdot {e^{ - {{[( - 4 \cdot i)/Maxiter]}^2}}}$$
(32)
$${\mathbf{X}}=({{\mathbf{X}}_{\mathbf{1}}}+{{\mathbf{X}}_{\mathbf{2}}}+{{\mathbf{X}}_{\mathbf{3}}})/3$$
(33)
$${\mathbf{X}}(t+1)={\mathbf{X}}+{\mathbf{X}} \cdot N(0,1)$$
(34)

This paper cites the idea of chromosome crossover and mutation operations to update the \(\:WAV\) vectors. Specifically, the \(\:WAV\) vector employs a two-point crossover operation with a crossover probability (\({P_c}=0.5\)). When the crossover probability is met, this paper randomly selects two positions in the \(WAV\) vector and generates two offspring strings by exchanging all elements between the positions of the two parent strings. Based on the construction pattern designed in this paper, the generated offspring are feasible solutions. Figure 4 illustrates an example of two-point crossover operators.

Fig. 4
figure 4

Two-point crossover operators for \(\:WAV\) vectors.

Full size image

The \(\:WAV\) employs a random mutation operation with a mutation probability as specified in Eq. (35). During the early stages of iteration, a higher mutation probability enhances the global optimization ability, while in the later stages of iteration, a lower mutation probability enriches the local optimization ability.

$${P_m}{\text{=}}0.5\cdot {e^{^{{ - {{[( - 4\cdot i)/Maxiter]}^2}}}}}$$
(35)

When the mutation probability is met, this paper randomly selects \(\:f\) positions in the parents, and each operation mutates into other elements in the corresponding assignment work teams set that can be assigned. Figure 5 illustrates an example of mutation operators.

Fig. 5
figure 5

Random mutation operators for \(\:WAV\) vectors.

Full size image

Procedure of the IGWO Algorithm

Figure 6 illustrates the workflow of the IGWO algorithm proposed in this paper. The specific process is as follows:

  • Step 1: Set the parameters of the IGWO algorithm and generate the population based on the methods described in section “Population initialization”.

  • Step 2: Calculate the fitness value of the population and determine the values of \(\:\alpha\:\), \(\:\beta\:\), and \(\:\delta\:\).

  • Step 3: Update the \(\:BSV\) and \(\:WAV\) vectors based on the individual update mechanism described in section “Individual position update” to form a new grey wolf population.

  • Step 4: Determine whether the number of iterations has reached Maxalt or meets the requirement to stop the iteration. If so, proceed to step 5; otherwise, return to step 2.

  • Step 5: Stop algorithm iteration and output the optimal iteration plan.

Fig. 6
figure 6

The workflow of the IGWO algorithm.

Full size image

Figure 7 takes the optimization process of a single population individual as an example to further clarify the process of how the proposed algorithm handles the DRCBFSP problem.

Fig. 7
figure 7

The optimization process of a single population individual.

Full size image

Experimental study

Test by 10 benchmark functions and analysis

Benchmark functions

Ten types of typical benchmark function are selected to evaluate the performance of the IGWO algorithm46, as outlined in Table 3. These functions encompass both unimodal (functions \({F_1}\)–\({F_5}\)) and nonlinear multimodal functions (\({\text{functions}}~{F_6}\)–\({F_{10}}\)).

Table 3 Ten types of typical benchmark functions.
Full size table

Comparative analysis of benchmark functions

To demonstrate the effectiveness and convergence efficiency of the IGWO algorithm, this paper compares it with several widely used and classic algorithms, including the Differential Evolution algorithm (DE), Whale Optimization algorithm (WOA), Particle Swarm Optimization algorithm (PSO), and basic GWO algorithm, for comparative analysis. This paper runs this comparative experiment on a computer with an Intel (R) Core (TM) i7 11,390 H @ 3.40 GHz processor, 16 GB memory, and Windows 11 operating system and solved by using MATLAB 2022 software programming. The initial population size of each algorithm is set to 30, and the maximum iterations are set to 1000. Each algorithm is run 30 times separately. Table 4 presents the average and variance of the 30 iterations, with the best values for each standard test function marked in bold. Parameters for the PSO algorithm are set as follows: \(c1=1.6\), \(c2=1.6\), \({w_{max}}=0.9\), \({w_{min}}=0.4\), and the speed v is limited to 20% of the upper and lower bounds of the problem47. Parameters for the DE algorithm is set as follows: a single-point crossover operation with a crossover probability of 0.6 and a discrete mutation operation with a mutation probability of 0.348.

Table 4 Comparative results of benchmark functions.
Full size table
  1. 1.

    Convergence accuracy and analysis.

In terms of mean values, the IGWO algorithm obtains significantly better solutions than the DE algorithm in the \({F_1}\)-\({F_6}\) and \({F_8}\)-\({F_9}\) functions. Additionally, both the IGWO and DE algorithms achieve the optimal solution in \({F_{10}}\). The IGWO algorithm also outperforms the WOA algorithm, obtaining considerably better solutions in the \({F_1}\)-\({F_6}\) and \({F_9}\), with both algorithms achieving the optimal solution in \({F_8}\) and \({F_{10}}\). the IGWO algorithm achieves better solutions than the PSO algorithm in functions \({F_1}\)-\({F_4}\), \({F_6}\)-\({F_{10}}\) and better solutions than the GWO algorithm in the functions \({F_1}\)-\({F_7}\), \({F_9}\)-\({F_{10}}\). Both the IGWO and GWO algorithms achieve the optimal solution in \({F_8}\). Therefore, the IGWO algorithm performs better in most standard test functions.

Regarding variance, the IGWO algorithm exhibits lower variances than the GWO algorithm in \({F_1}\)-\({F_7}\) and \({F_{10}}\). The variances in \({F_8}\)-\({F_9}\) functions are 0, indicating that the IGWO algorithm is more stable than the GWO algorithm.

While the IGWO algorithm performs well in most standard test functions, there remains a gap between the IGWO algorithm and the actual optimal solution in \({F_5}\) and \({F_7}\). Thus, there is potential for further improvement in future research.

  1. 2.

    Convergence curves and analysis.

Figure 8 displays the optimization curves of the five optimization algorithms for the ten standard test functions. The IGWO algorithm exhibits the fastest convergence rate in single-mode normal test functions \({F_1}\)-\({F_4}\). Furthermore, it demonstrates better searchability in non-linear multi-mode functions \({F_6}\), \({F_8}\)-\({F_{10}}\).

Therefore, according to the performance of the IGWO algorithm in most function optimization problems, it exhibits advantages over other contrast algorithms in terms of solution accuracy and convergence rates.

Fig. 8
figure 8figure 8

Algorithm convergence graph.

Full size image

Numerical experiment

To compare the IGWO algorithm with other algorithms more reasonably in discrete problems, 18 datasets from the classic example49 (VFR data) are selected for numerical experiments. The two constraints of work teams and spare parts are considered in this paper. Therefore, it is necessary to randomly modify the dataset about work teams, production efficiency and consumption of spare parts as well as buffer capacity. The 18 datasets contain 6 data scales, and each data scale involves 3 distinct test datasets, as shown in Table 5. To verify the superiority of the IGWO algorithm, this paper compared it with two algorithms: Improved Genetic Algorithm50 which shows excellent performance in job scheduling problems, and basic GWO algorithm. To ensure the fairness, 10 experiments were conducted with the same population size (\(N=80\)), the same maximum iteration number (\({T_{max}}=300\)) and the same termination criteria (reaching the maximum number of iterations). This paper runs this comparative experiment on a computer with an Intel (R) Core (TM) i7 11,390 H @ 3.40 GHz processor, 16 GB memory, and Windows 11 operating system and solved by using MATLAB 2022 software programming.

Table 5 Specific parameters of VFR datasets.
Full size table

The Percentage Relative Deviation (\(RPD\)) values are calculated using Eq. (36), where\({f_{ct}}\) denotes the experimental value obtained in each experiment and \({f_{cb}}\) represents the best fitness value obtained across all algorithms51.

$$RPD=({f_{ct}} - {f_{cb}})/{f_{cb}}$$
(36)

Table 6 presents the RPD of the best fitness value (Best), average fitness value (Average), and computing time (CT) for IGWO and other tested algorithms after solving instances VFR01 ~ 18. The results clearly demonstrate that IGWO outperforms the other algorithms across the range of tested problem scales. Although the computing time of IGWO is higher than that of BGWO for instances of the same scale, the additional computational cost is justified and remains fully acceptable within the context of scheduling optimization for ship plane block flow lines.

Table 6 The RPD values from the comparative experiment.
Full size table

The violin plots in Fig. 9 illustrate the solution distribution for all algorithms across datasets VFR01-VFR18. The plots show that the IGWO algorithm demonstrates better performance in both best solutions and average solutions, across both small and large problem scales. Additionally, the IGWO algorithm effectively avoids getting stuck in local optima, highlighting its robustness in solving multimodal optimization problems.

Fig. 9
figure 9figure 9figure 9

Solution results of the compared algorithms.

Full size image

Case verification

To verify the mathematical model and the applicability of the IGWO algorithm to the DRCBFSP problem directly, this paper integrates ship plane block production data from the shipyard for scheduling optimization. The information regarding blocks, workstations, and spare parts is presented in Table 7. There are 20 blocks to be assembled (\({I_1}\)–\({I_{20}}\)), along with three types of spare parts (\({R_1}\)–\({R_3}\)). The flow line is equipped with 8 stations (\({J_1}\)–\({J_8}\)), and the corresponding work efficiency of work teams at each station is detailed in Table 8. If the work task of block 2 on the 3rd station is assigned to the eligible work team (\({P_5}\)), the processing time of the work task would be 6 considering the efficiency level. Finally, the production efficiency of various spare parts and the buffer capacity equipped are as shown in Table 9.

Table 7 Block-station—resource information of the instance.
Full size table
Table 8 Station-Work team information of the instance.
Full size table
Table 9 Resource-buffer information of the instance.
Full size table

In this case verification, 20 experiments are carried out by IGWO, GWO, and GA algorithms with a population size of 80 and a maximum of 300 iterations. The assignment of work teams and the assembly sequence planning of blocks when solving the actual shipyard problem can be observed in Fig. 10. The convergence curves of the proposed algorithm and the other two algorithms for solving this problem are depicted in Fig. 11. The IGWO algorithm consistently obtains superior values compared to the others. Specifically, compared with the solution results of the GA algorithm and the GWO algorithm, the block manufacturing time solved by the IGWO algorithm has been reduced by 14 h and 13 h, respectively, while its manufacturing efficiency has been enhanced by 8.54% and 7.98%, respectively. Therefore, the problem model and algorithm proposed in this paper have good applicability for solving the DRCBFSP problem.

Fig. 10
figure 10

Gantt chart of the optimal scheduling scheme.

Full size image
Fig. 11
figure 11

Iterative comparison of three algorithms.

Full size image

Since this problem is a multimodal problem, the GWO algorithm takes advantage of the dynamic hierarchy of α, β, and δ wolves to progressively narrow the search space, ensuring a balance between global and local searches. This results in strong global and local search capabilities, with fewer parameters, making it suitable for handling complex optimization problems such as nonlinear, multimodal, and multi-constraint issues. While Genetic Algorithm (GA) is a classic optimization method, its effectiveness can vary across different problems, and it may struggle to find global optima in complex combinatorial or discontinuous problems. However, GWO has certain limitations, such as a higher dependency on the initial solution and a tendency to get stuck in local optima. To address these issues, this paper incorporates nonlinear search factors, dynamic inertia weight factors, and Gaussian mutation perturbation strategies to enhance the algorithm’s exploitation and exploration capabilities. The experimental results in this paper also fully demonstrate the effectiveness of these improvements.

Conclusions and future research

This paper addresses the scheduling optimization of ship plane block flow lines, considering the dual resource constraints typical of shipbuilding operations, such as work teams and spare parts. This area has been relatively underexplored in academic research, and our work aims to fill this gap while providing practical guidance for improving operational efficiency in shipbuilding workshops. The main conclusions from this study are summarized as follows:

By extending traditional flow line scheduling models, we formulate a mathematical model that aligns with the actual constraints including spare parts and work teams faced in workshops and the objective is to minimize the completion time. To solve the above problem, a MILP model is formulated to determine the plane block assembly sequence, worker teams allocation and timetables for assembly. Besides, IGWO with nonlinear search factors, dynamic inertia weight factors, and Gaussian mutation perturbation strategies are developed to address the identified problem. Ultimately, the efficacy of the proposed approach is validated through three types of comprehensive experimental studies.

The results indicate that our approach can improve production efficiency by over 7% in real ship plane block flow lines. We recommend that practitioners in the shipbuilding industry adopt this method to optimize their scheduling processes. Future research could explore further refinements to the algorithm and investigate its applicability to other manufacturing contexts, thus enhancing the overall utility and adaptability of the proposed framework.

In the following study, it is essential to consider the dynamic scheduling problems caused by machine breakdown, emergency plugins, uncertainty in the work team, and other unexpected events with the dual resource constraints to better meet the applicability of workshop operations further.