Abstract
Particle Swarm Optimization (PSO), a meta-heuristic algorithm inspired by swarm intelligence, is widely applied to various optimization problems due to its simplicity, ease of implementation, and fast convergence. However, PSO frequently converges prematurely to local optima when addressing single-objective numerical optimization problems due to its inherent rapid convergence. To address this issue, we propose a hybrid differential evolution (DE) particle swarm optimization algorithm based on dynamic strategies (MDE-DPSO). In our proposed algorithm, we first introduce a novel dynamic inertia weight method along with adaptive acceleration coefficients to dynamically adjust the particles’ search range. Secondly, we propose a dynamic velocity update strategy that integrates the center nearest particle and a perturbation term. Finally, the mutation crossover operator of DE is applied to PSO, selecting the appropriate mutation strategy based on particle improvement, which generates a mutant vector. This vector is then combined with the current particle’s best position through crossover, aiding particles in escaping local optima. To validate the efficacy of MDE-DPSO, we evaluated it on the CEC2013, CEC2014, CEC2017, and CEC2022 benchmark suites, comparing its performance against fifteen algorithms. The experimental results indicate that our proposed algorithm demonstrates significant competitiveness.
Similar content being viewed by others
Introduction
Problems in engineering can be formulated as numerical function optimization problems1. Most of these problems are complex in nature with multiple peaks, high dimensions, or non-differentiability. Traditional optimization techniques struggle to find exact solutions for such complex problems. This led to the emergence of meta-heuristic algorithms (MAs), which are high-level heuristics designed to find approximate solutions by extensively exploring the solution space. MAs are adaptable and flexible, making them widely used across various fields, including artificial intelligence, power systems, healthcare, finance, and science2,3,4,5,6,7.
In the past decades, researchers have proposed many meta-heuristic algorithms, which can be summarized as single-solution based algorithms and population-based algorithms.Common single-solution algorithms, such as simulated annealing (SA)8 and taboo search (TS)9, deal with only one solution at each step and usually rely on neighborhood search or other local search strategies to improve the current solution, and thus easily fall into a local optimum. On the other hand, population-based algorithms deal with multiple solutions simultaneously at each step, improve the quality of solutions through collaboration and competition among individuals in the population, have powerful exploration capabilities, and have attracted the attention of more and more researchers.
Population-based algorithms can be broadly classified into evolutionary algorithms (EAs) and swarm intelligence optimization algorithms (SIOA). EAs are a subset of population-based optimization methods that improve solution quality by simulating natural evolution processes like selection, mutation, and inheritance. Notable EAs algorithms include genetic algorithms (GA)10, differential evolution (DE)11, and genetic programming (GP)12. Recent innovations in EAs include a differential evolution algorithm with exponential crossover (DE-EXP)13 and a co-evolutionary differential evolution algorithm (PaDE-pet)14. In contrast, SIOA achieve a balance between global exploration and local exploitation by leveraging collaboration and information sharing among individuals, offering enhanced adaptability and robustness. Among the diverse SIOA, animal group behaviors have inspired many algorithms. For instance, particle swarm optimization (PSO)15 simulates bird flocking behavior. The seahorse optimizer (SHO)16 is inspired by seahorses’ complex movements, while the grey wolf optimizer (GWO)17 mimics the hierarchical hunting strategies of grey wolves. The spider wasp optimizer (SWO)18 replicates the behaviors of spider wasps, providing a biologically inspired optimization method. This algorithm features distinct update strategies, suitable for various optimization problems with different exploration and exploitation needs. Additionally, some algorithms are inspired by physical laws, such as the optical microscope algorithm (OMA)19 and the kepler optimization algorithm (KOA)20. Some algorithms are inspired by mathematical principles, such as the sine cosine algorithm (SCA)21 and the exponential distribution optimizer (EDO)22.
PSO is a group intelligence algorithm proposed by Kennedy and Eberhart in 1995. Its core idea is to use the sharing of information by individuals in the group to make the movement of the whole group produce an evolution process from disorder to order in the problem solution space, so as to obtain a feasible solution to the problem. In the iterative process of the PSO algorithm, each individual (particle) is guided by its historical best position and the global best position found by the whole dynamic population to explore possible solutions. Although the PSO algorithm has the advantages of being easy to implement and having low computational complexity, it often faces issues such as premature convergence and limited global search capability in practical optimization problems.
To address these issues, researchers have proposed a series of improvements, including variants, hybridisation, etc. In the MPSO algorithm23, the authors propose a chaos-based nonlinear inertia weight to help particles better balance the exploration and utilisation of the solution space. In addition, an adaptive position update strategy is introduced to further balance the exploration and utilisation processes. In order to solve the single-objective numerical optimization problem, Meng et al.24 proposed a fully informed search scheme based on the global optimum of each generation, which makes use of the knowledge of the whole population to guide the global optimal particles out of their current positions, well avoiding the problem of premature convergence. In addition, some researchers have hybridised DE’s mutation operator in PSO in order to enhance the searching ability and population diversity of the particles25,26,27. Through the variation operation, it effectively helps particles caught in local minima to explore higher quality solutions. Although these improved PSO variants outperform the original PSO algorithm in terms of optimization performance, to the best of our knowledge, there is still room for further improvement in terms of solution diversity and convergence speed. This is what motivates our research.
In order to further enhance the diversity of solutions and the speed of convergence, we propose a hybrid differential evolution particle swarm optimization algorithm based on dynamic strategies (MDE-DPSO), which has the following main highlights:
-
(1)
Our algorithm employs a parametric strategy incorporating new inertia weights and acceleration coefficients to more effectively balance the ability of global and local search by dynamically adjusting the search range of the particles, thereby accelerating the convergence process.
-
(2)
During the iterative process, we adopt a dynamic velocity update strategy that includes the center nearest particle and the perturbation term. This strategy enhances the ability of individual particles to obtain effective information during the global search by referring to the optimal particles near the centre position, thus more effectively helping particles to adjust their direction and speeding up the convergence speed. Meanwhile, the perturbation term is introduced to increase the randomness of exploration.
-
(3)
The mutation crossover operator of DE is applied to PSO. The operator combines two variational strategies to enhance the diversity of candidate solutions by reasonably exploiting the properties of each strategy, thus helping the particle swarm to jump out of the local optimum and improve the overall optimization performance.
-
(4)
The algorithm is validated using all benchmark test functions from the CEC2013, CEC2014, CEC2017, and CEC2022 test suites, and the analysis of the results shows that MDE-DPSO is highly competitive compared to other algorithms.
The rest of the paper is organized as follows. Section "Related works" presents the classical PSO algorithm and other variants. Section "The MDE-DPSO algorithm" presents the MDE-DPSO algorithm proposed in this paper. The section "Experiment analysis" analyzes the new algorithm experimentally. Finally, in Section "Conclusion", the work we have done is summarized.
Related works
Classical PSO algorithm
PSO searches for an optimal solution in the solution space by a group of particles, each representing a potential solution. The particles update their velocity and position by keeping track of their own historical optimal position (Pbest) and the historical optimal position of all particles (Gbest). The position and velocity of each particle are updated by the following equation:
where \(t\) denotes the iteration number, \(w\) denotes the inertia weight, and \(c_1\) and \(c_2\) are acceleration coefficients. The terms \(r_1\) and \(r_2\) are random numbers in the range \([0,1]\).
Improved PSO algorithm
Over the past decades, researchers have proposed various PSO variants that can be broadly classified into three categories: improvements in learning strategies, parameter tuning, and hybridisation with other algorithms.
Learning strategy is an important factor that affects the performance of the algorithm and determines how the particles use information about themselves and other particles to update the position and velocity. CLPSO algorithm28 utilizes a comprehensive learning strategy, so that the particles can learn from multiple neighborhood optimal particles, thus enhancing the search capability. Wang et al.29 proposed an optimization by particle swarm optimization (OBPSO) algorithm based on generalized opposition learning and Cauchy mutation, which enhances the exploration ability and diversity of particles through the generalized opposition learning strategy and Cauchy mutation. In RSPSO30, the useful information in the population is retained by mixing a newly proposed dimensional learning strategy. Li et al.31 proposed a pyramid PSO (PPSO) with novel competitive and cooperative strategies to update the particle information.
The inertia weight (\(\omega\)) and acceleration factor are the most important parameters of the PSO. The inertia weight determines the influence of a particle’s current velocity on its next velocity, while the acceleration coefficients control the extent to which a particle is attracted to its personal best solution and the global best solution. A larger \(\omega\) facilitates global exploration, whereas a smaller \(\omega\) is more suitable for local exploitation32. To achieve a balance between global exploration and local exploitation, researchers have proposed various improvements to the inertia weight in recent years, including chaotic, linear/nonlinear decrement, and adaptive adjustments. For instance, in the MPSO23, a nonlinear chaotic inertia weight adjustment strategy was introduced to better balance the global exploration and local exploitation capabilities of PSO. Duan et al.33 combined linear and nonlinear methods to adaptively adjust the inertia weight, thereby enhancing the particles’ local and global search abilities. Furthermore, Tian et al.34 found that using sigmoid-based acceleration coefficients can effectively balance the particles’ global search ability in the early stages and their global convergence ability in the later stages. These methods provide valuable references for improving the performance of PSO.
According to the no free lunch theorem35, no single MAs can solve all optimization problems. As a result, researchers have become increasingly interested in combining the PSO algorithm with other optimization methods. Among these, the hybridization of DE and PSO has become a commonly used approach for improvement. Liu et al.36 proposed a hybrid PSO-DE algorithm, where DE is used to update the particle’s previous best position. Sayah and Hamouda37 introduced an effective combination strategy of DE and PSO, named DEPSO, for optimizing the economic load dispatch (ELD) problem in power generation. Zhai and Jiang38 developed a new hybrid DE and adaptive PSO (DEPSO) method for identifying targets obscured by leaves. Experimental results demonstrate that the proposed method is effective and robust in target detection through leaves. To address the stagnation problem in the time-optimal turn maneuvering problem with path constraints, Melton et al.39 combined PSO with DE, showing excellent performance. The computation time required was reduced by 40% compared to using DE alone for the same problem. Mohammadi et al.40 integrated a multi-layer perceptron (MLP) with PSO, which was further combined with DE for optimizing river suspended sediment load (SSL). In the HGPSODE algorithm proposed by Dadvar et al.41, DE and PSO collaborate based on nash bargaining theory, leading to significant improvements in the search for the optimal solution. Yuan et al.42 applied the concept of “cooperative win-win” to combine DE and PSO, improving PSO’s convergence accuracy and addressing the premature convergence issue in mobile robot path planning. It can be seen that by combining the two distinct methods, DE and PSO, greater performance improvements can be achieved compared to using either method alone.
The MDE-DPSO algorithm
In this section, we will introduce a new PSO variant, named MDE-DPSO. The algorithm improves performance through three main aspects: 1) introducing a new dynamic parameter adjustment strategy; 2) adopting a dynamic velocity update strategy that combines the center nearest particle and a perturbation term; 3) applying a mutation crossover operator with two mutation strategies to PSO.
Dynamic parameter adjustment strategy
Cosine-decreasing inertia weight
The inertia weight (\(\omega\)) is a key parameter in the PSO algorithm, significantly impacting the global search ability by enhancing population diversity and accelerating convergence43. Higher \(\omega\) values help improve global search capability, while lower \(\omega\) values enhance local search capability. However, maintaining a fixed \(\omega\) may lead to an insufficient balance between global search and local exploitation, potentially missing the global optimum. Both linear and nonlinear inertia weights effectively address this issue. The linear-decreasing inertia weight is commonly used for its simplicity, but its rigidity can lead to premature convergence. In contrast, the periodic cosine-decreasing inertia weight proposed in this paper, as shown in Eq. (2), allows for a smoother and more adaptive transition between exploration and exploitation. The settings of the parameters \(w_{\text {max}}\) and \(w_{\text {min}}\) refer to the research results of Shi and Eberhart44.
where \(w_{\text {max}}=0.9\), \(w_{\text {min}}=0.4\), \(\text {t}\) is the current iteration number, and \(\text {T}_{\text {max}}\) is the maximum iteration number.
As stated in (2), \(\cos \left( \frac{\pi }{2} \cdot \frac{\text {t}}{\text {T}_{\text {max}}} \right)\)is a cosine function that smoothly transitions from 1 to 0. As \(\text {iter}\) changes from 0 to \(\text {T}_{\text {max}}\), this term transitions smoothly from \(\cos (0) = 1\) to \(\cos \left( \frac{\pi }{2}\right) = 0\).
As can be seen from Fig. 1, compared to the linear-decreasing inertia weight, the cosine-decreasing inertia weight better balances global exploration and local exploitation, rather than simply varying. In Section "Ablation experiment", we will further compare the performance of these two types of inertia weights using the benchmarks of the CEC2013 test suite on the 30D optimization.
Variation curves of cosine-decreasing inertia weight versus linear-decreasing inertia weight.
Sine-cosine acceleration factor
In the PSO algorithm, the acceleration coefficients \(c_1\) and \(c_2\) are the key parameters, which determine the speeds of the particles moving to the individual best position and the global best position. In traditional PSO, the acceleration coefficient is usually a constant 2. This design, although simple, has some shortcomings in practical applications, which cannot be dynamically adjusted according to the needs of different stages, and may lead to insufficient exploration in the early stage or insufficient development in the later stage. In the optimization process, the early stage requires strong exploration ability to jump out of the local optimal solution, while the later stage requires strong development ability to search the optimal solution finely, and the constant learning factor is difficult to take care of these two needs at the same time.
Therefore, it is considered to take advantage of the periodicity of the sine and cosine functions to make the acceleration coefficients change continuously during the iteration process, so as to dynamically adjust the search behavior of the particles. At the same time, it can provide a smooth change curve, avoiding the impact of sudden changes in acceleration coefficients on the stability of the algorithm, and ensuring strong pre-search ability for the particles, as well as strong post-exploitation ability. The update equations for the learning factors are shown in Eqs. (3) and (4).
-
(1)
Logarithmic section:
\(\log \left( 1 + \left( \frac{\text {t}}{\text {T}_{\text {max}}} \right) \cdot (\exp (1) - 1)\right)\) causes larger changes at the beginning and smaller changes later, modeling a rapid adjustment process in the early stages and a gradual convergence in the later stages.
-
(2)
Cosine and sine section:
\(\left( 1 - \log \left( 1 + \left( \frac{\text {t}}{\text {T}_{\text {max}}} \right) \cdot (\exp (1) - 1)\right) \right) \cdot \frac{\pi }{2}\) ensure the smooth transition of the learning factors through the sine and cosine functions.
Dynamic velocity update strategy
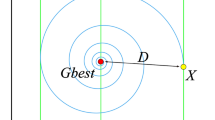
The velocity update of traditional PSO combines the current velocity of the particle, the Pbest and the Gbest to calculate the new velocity. This leads to a gradual concentration of the particle population in one sub-region, which prevents effective exploration of other potential optimal regions.Specifically, the Pbest and Gbest are so close to the current particle positions that the velocities may become very small or even zero, making it impossible for the particles to move further and thus fall into a local optimum. Generally speaking, the center of the group (Center) is not too far away from the Gbest and may exist around it, and the one closest to the center of the particle swarm is very likely to find the Gbest as a result. Therefore, the current position of the closest particle to the center region (CNPpos) is considered to be added to the original velocity formula to increase the momentum of the particle to move towards the center position.Where Center and CNPpos are generated by Eqs. (5) and (6). In addition, in order to be able to make the search of particles broad, the inclusion of a perturbation term strategy (Perturbation) is chosen, as shown in Eq. (7).
In summary, the updated velocity formula dynamically incorporates CNPpos and Perturbation, enabling particles to escape local optima. The new velocity update equation is presented in Eq. (8).
where the term \(\frac{1}{N}\) is normalized by the number of particles \(N\), and the term \(\sum _{i=1}^{N} X_{i}^{t}\) sums up the positions of all the particles at time \(t\).
where \(Distances_i\) denotes the Euclidean distance between the position of the i-th particle and the center position, \(\text {Closest\_idx}\) represents the index of the particle closest to the center, and \(CNPpos^t\) denotes the position of the nearest particle to the center at the t-th iteration.
where \(Perturbation\_strength\) denotes the strength of the Perturbation, set to 0.01; rand(N, D) generates a matrix of size \((N\times D)\) with random values between 0 and 1. \(Perturbation\) is the resulting matrix with Perturbations applied, with values in the range \([-0.005, 0.005]\).
where \(w\) is generated by Eq. (2), \(c_1\) and \(c_2\) are generated by Eqs. (3) and (4), respectively; \(r_1\) and \(r_2\) are random numbers in the range \([0,1]\); \({Pbest}_{i}^{t}\) is the historical best position of the \(i\)-th particle at time \(t\); \({Gbest}^{t}\) is the global best position at time \(t\); and \({CNPpos}^{t}\) is the position of the nearest particle to the center at the \(t\)-th iteration.
The mutation crossover operator
PSO algorithm has a fast convergence speed, but it is easy to fall into local optimality and lack of population diversity in the late search stage. And DE, as an efficient global optimization algorithm, has been widely used to solve complex real-world optimization problems45. Therefore, in this paper, the mutation crossover operator of DE is applied to PSO to help particles escape from local optima by generating candidate solutions. Regulated DE includes four basic steps: initialization, mutation, crossover, and selection. In this paper, it is uniformly referred to as the mutation crossover operator.
Mutation strategies influence the search direction of DE, making the choice of an appropriate strategy particularly crucial. Common mutation strategies include DE/rand/1, DE/rand/2, DE/best/1, and DE/best/2. Additionally, in order to achieve a balance between exploration and exploitation, Zhang et al.46 introduced a mutation strategy incorporating an external archive, known as the “DE/current-to-pbest/1” strategy, which has since been widely adopted by most DE variants or similar approaches. During the iteration process of PSO, the quality of particles varies, and using a single mutation strategy may destroy the characteristics of the particles. Therefore, this paper utilizes two mutation strategies: DE/rand/1 to enhance particle exploration, and DE/current-to-pbest/1 to facilitate local exploitation.
In the mutation crossover operator, we design an indicator to effectively combine two mutation strategies. The corresponding mutation strategy is dynamically selected based on the number of iterations in which a particle has not improved. Experimental results show that this approach enhances particle diversity and strengthens the ability to escape local optima. Specifically, particles are categorized based on whether the condition \(\text {unimproved\_num} \ge \text {limit\_num}\) holds. The Gbest particle bypasses this condition and is directly assigned to the industrious population. If the condition is met, it indicates that the particle’s fitness has stagnated for a certain number of iterations. In such cases, the particle is categorized into the lazy population, and the DE/rand/1 strategy is used to facilitate a broader search. On the other hand, if the condition is not met, the particle remains in the industrious population and employs the DE/current-to-pbest/1 strategy, which supports more focused optimization. Here, \(\text {unimproved\_num}\) refers to the number of consecutive iterations during which a particle’s fitness has not shown improvement. This value helps to track stagnation in the search process. If \(\text {unimproved\_num} \ge \text {limit\_num}\), it suggests that the particle has not made significant progress and thus is placed in the lazy population. The parameter \(\text {limit\_num}\) serves as a threshold that determines when the particle is considered to be stagnating. The DE/rand/1 and DE/current-to-pbest/1 strategies are formulated according to Eqs. (9) and (10), respectively. In particular, if a particle in the lazy population improves its fitness in subsequent iterations, its \(\text {unimproved\_num}\) is reset, allowing it to rejoin the industrious population and continue optimization with the DE/current-to-pbest/1 strategy.
where \(X_{r1}\), \(X_{r2}\), and \(X_{r3}\) are randomly selected individuals from the entire population, with \(r_{1} \ne r_{2} \ne r_{3}\). The scaling factor \(F\) is fixed at 0.5.
where \({V_{i}}\) denotes the mutation vector of the \(i\)-th particle, \({X_{i}}\) is the current position of the \(i\)-th particle, \({X^{p}_{\text {best}}}\) is the position of a particle randomly selected from the top \(p\%\) individuals in the population, \({X_{r4}}\) is a randomly selected position from the current population, and \({\tilde{X}}_{r5}\) is a randomly selected position from either the external archive (which stores high-quality solutions) or the current population. \(F\) is as defined in Eq. (9), and \(p\) is set to 20.
After generating the mutation vectors, a crossover operation is performed as per Eq. (11), followed by evaluation according to Eq. (12). If the candidate solution improves the current particle’s Pbest, the particle’s best fitness value and position are updated. If it improves the Gbest, the global best value and position are updated. If neither condition is met, no updates are made. Finally, the archive is updated: if the new candidate’s fitness is better than the worst in the archive, the worst solution is replaced with the new one.
where \(\text {U}_{i,j}\) is the \(j\)-th component of the trial vector of the \(i\)-th particle, \(V_{i,j}\) is the \(j\)-th component of the mutation vector of the \(i\)-th particle, \(X_{i,j}\) is the \(j\)-th component of the current position of the \(i\)-th particle, \(cr_i\) is the crossover probability, and \(j_{\text {rand}}\) is a randomly chosen index to ensure that at least one dimension from the mutation vector \(V_{i,j}\) is used.
where if the trial vector \(U_{i}\) has a better fitness value than the current position \(X_{i}\) or the \(Gbest\), they will be updated accordingly. Otherwise, they remain unchanged. Algorithm 1 gives a detailed description of the MDE-DPSO.
Pseudo code of the MDE-DPSO algorithm
Experiment analysis
This section uses 100 benchmark functions from the CEC2013, CEC2014, CEC2017,and CEC2022 test suites for real-parameter single-objective optimization, with the aim of evaluating the performance of the proposed algorithm in terms of accuracy and convergence speed. The benchmarks of the test suite can be divided into four groups: single-peak, multi-peak, hybrid, and combinatorial functions. Among them, \(f_{a1}\)-\(f_{a5}\) are single-peak, \(f_{a6}\)-\(f_{a20}\) are multi-peak, and \(f_{a21}\)-\(f_{a28}\) are combinatorial functions in CEC2013; \(f_{b1}\)-\(f_{b3}\) are single-peak, \(f_{b4}\)-\(f_{b16}\) are multi-peak, \(f_{b17}\)-\(f_{b22}\) are hybrid functions, and \(f_{b23}\)-\(f_{b30}\) are combinatorial functions in CEC2014; \(f_{c1}\)-\(f_{c3}\) are single-peak, \(f_{c4}\)-\(f_{c10}\) are multi-peak, \(f_{c11}\)-\(f_{c20}\) are hybrid functions, and \(f_{c21}\)-\(f_{c30}\) are combinatorial functions in CEC2017; \(f_{d1}\) is single-peak, \(f_{d2}\)-\(f_{d5}\) are basic functions, \(f_{d6}\)-\(f_{d8}\) are hybrid functions, and \(f_{d9}\)-\(f_{d12}\) are combinatorial functions in CEC2022.
The comparison algorithms include PSO variants, and other meta-heuristic algorithms.The PSO variants include the modified particle swarm optimization algorithm with adaptive policies (MPSO)23, a novel particle swarm algorithm with hybrid paradigms and parameter adaptive schemes (PSO-sono)24, particle swarm optimization algorithms driven by elite profiles (EAPSO)47, a particle swarm optimization algorithm based on Hummingbird flight patterns (PSO-HBF)48, multiple adaptive co-evolutionary particle swarm optimization (ACEPSO)49, a dynamic probability mutation particle swarm optimization with chaotic inertia weight (CWDEPSO)50, dual fitness PSO (DFPSO)51, and a sequential quadratic programming based strategy for particle swarm optimization (SQPPSO-sono)52; other meta-heuristic algorithms include cheetah optimizer (CO)53, the honey badger algorithm (HBA)54, artificial rabbit optimization (ARO)55, optical microscope algorithm (OMA)19, a novel population-based meta-heuristic algorithm called the exponential distribution optimizer (EDO)22, hybrid WOA algorithm that combines Lévy flight and differential evolution (WOA-LFDE)56, and JADE algorithm46. All comparison algorithms use the parameter configurations recommended by the authors, and the specific parameter values are listed in Table 1.
All experiments were performed on a Matlab version 2022a personal computer with an AMD Ryzen 9 7945HX 2.50 GHz CPU and a Microsoft Windows 11 Enterprise 64-bit operating system. The maximum number of evaluations for algorithm validation is set to \(10000 \times D\), where D represents the problem dimension. Each algorithm was run independently 51 times to obtain the mean value and standard deviation of the fitness error. We used the Wilcoxon signed-rank test with a significance level of \(\alpha =0.05\) and the Friedman test to determine whether there were significant differences between the algorithms. The symbols “>”, “<”, and “\(\approx\)” denote “significantly better” “significantly worse” and “similar” respectively. This section is organized as follows: optimization accuracy comparison in section "Optimization accuracy comparison", convergence analysis of our algorithm in section "Convergence analysis", ablation experiments in section "Ablation experiment", parameter settings in section "Parameter settings". Finally, the algorithm complexity is presented in section "Algorithm time complexity".
Optimization accuracy comparison
Test on the CEC2013, CEC2014, and CEC2017 test suites
The optimization results of the eleven recent algorithms and our MDE-DPSO algorithm are compared under the 10D, 30D, 50D CEC2013, CEC2014, and CEC2017 test sets, and the results are shown in Tables 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, respectively. In the table, the values before the symbol “/” represent the mean, while those after the “/” represent the standard deviation. The values in parentheses indicate the comparison results between each algorithm and MDE-DPSO. The best values are shown in bold. For example, the result of the MPSO algorithm on the 30D CEC2013 test suite for the function \(f_{a1}\) is “3.3202E-04/7.7069E-04 (<)”. Here, “3.3202E-04” and “7.7069E-04” represent the mean error and standard deviation achieved by the algorithm, respectively, with “E-04” denoting the scientific notation for the magnitude. The symbol “<” indicates that the performance of MPSO is significantly worse than that of MDE-DPSO. From the comparison results, it is evident that the MDE-DPSO algorithm demonstrates outstanding performance on the 10D, 30D, and 50D optimization tasks across multiple test sets. Notably, on 10D optimization tasks, MDE-DPSO achieves more significant performance gains compared to its results on 30D and 50D. This is evident from its best values achieved on 13, 15, and 13 functions on the 10D CEC2013, CEC2014, and CEC2017 test suites, respectively. This also demonstrates that the MDE-DPSO algorithm is very generalizable, and not just good on a particular test suite. At the same time, we have consolidated the results from Tables 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19 into Table 20. From Table 20, it can be seen that our MDE-DPSO algorithm is very competitive with other algorithms, achieving much better or similar performance. Specifically, the MDE-DPSO algorithm obtained 182 performance improvements and 8 similarities in 264 cases compared to MPSO, 154 performance improvements and 13 similarities in 264 cases compared to PSO-sono, 166 performance improvements and 13 similarities in 264 cases compared to EAPSO, 187 performance improvements and 6 similarities in 264 cases compared to PSO-HBF, 160 performance improvements and 16 similarities in 264 cases compared to ACEPSO, 178 performance improvements and 7 similarities in 264 cases compared to CO, 248 performance improvements and 6 similarities in 264 cases compared to HBA, 175 performance improvements and 8 similarities in 264 cases compared to ARO, 229 performance improvements and 6 similarities in 264 cases compared to OMA, 212 performance improvements and 5 similarities in 264 cases compared to EDO, and 200 performance improvements and 7 similarities in 264 cases compared to WOA-LFDE. Finally, we conducted Friedman test to compare the experimental results of five PSO variants and six meta-heuristic algorithms with our MDE-DPSO algorithm on the 10D, 30D, and 50D CEC2013, CEC2014, and CEC2017 benchmark suites, as shown in Tables 21 and 22. Specifically, Table 21 presents the comparison results between the PSO variants and MDE-DPSO, while Table 22 shows the comparison between the meta-heuristic algorithms and MDE-DPSO. To make the rankings more intuitive, we plotted the average rankings of each algorithm in Figs. 2 and 3. Lower average ranking means better algorithm performance. Experimental results show that the MDE-DPSO algorithm performs exceptionally well compared to other PSO variants, achieving a total of 8 lowest rank length scores. In comparison with other meta-heuristic algorithms, it obtained 8 lowest rank length scores, further validating its superior performance.
Comparison of the average ranking of the MDE-DPSO algorithm with the five PSO variants on different dimensions (10D, 30D, 50D) in the CEC2013, CEC2014 and CEC2017 benchmarks.
Comparison of the average ranking of the MDE-DPSO algorithm with the six meta-heuristic algorithms on different dimensions (10D, 30D, 50D) in the CEC2013, CEC2014 and CEC2017 benchmarks.
Test on the CEC2022 test suite
Based on the reviewers’ suggestions, we also validated the CEC2022 test suite in 10D and 20D. The comparison algorithms included JADE46, CWDEPSO50, DFPSO51, and SQPPSO-sono52. JADE is a widely recognized adaptive differential evolution algorithm. CWDEPSO improves the parameter settings and algorithmic mechanisms to effectively address the challenges of premature convergence and local optimization in real-world engineering optimization problems. DFPSO accurately evaluates particle fitness and diversity, and integrates the ability to evaluate these features. SQPPSO-sono is a recently proposed PSO variant that integrates the SQP method with NRAS into particle swarm optimization, demonstrating strong performance in single-objective numerical optimization problems. These considerations guided our selection of these algorithms for comparison. The comparative results are presented in Tables 23 and 24, with a summary provided in Table 25. The best values are shown in bold. As shown in Table 25, MDE-DPSO achieved 14 improvements and 2 ties compared to the JADE algorithm; 19 improvements and 3 ties compared to CWDEPSO; 23 improvements and 0 ties compared to DFPSO; and 19 improvements and 3 ties compared to SQPPSO-sono. Compared to these comparison algorithms, the MDE-DPSO algorithm still performs excellently on new test suite. MDE-DPSO introduces a mutation crossover operator based on PSO, using mutation strategies flexibly to help the algorithm conduct diversified searches in complex search spaces, which enables it to perform excellently on hybrid functions (\(f_{d6}\)-\(f_{d8}\)) and composite functions (\(f_{d9}\)-\(f_{d12}\)).However, the performance of the MDE-DPSO algorithm is poor on unimodal function (\(f_{d1}\)), as such functions have only a single optimal solution and require more precise searching. Our mutation strategy is selected based on the particle’s improvement, which makes it difficult for particles to stay focused around the optimal solution for an extended period during the search process, thus affecting their ability to quickly converge to the optimal solution. Finally, we conducted Friedman test to compare the experimental results of four excellent algorithms with our MDE-DPSO algorithm on the 10D, and 20D CEC2022 benchmark suite, as shown in Table 26. Similarly, we plotted the average ranking of each comparison algorithm in Fig. 4. It can be observed that, on the new test suite, our MDE-DPSO algorithm still achieves a competitive ranking compared to other advanced algorithms, receiving the lowest rank length scores on both dimensions.
Comparison of the average ranking of the MDE-DPSO algorithm with JADE, CWDEPSO, DFPSO, and SQPPSO-sono on different dimensions (10D, 20D) in the CEC2022 benchmarks.
Convergence analysis
Convergence curves and box plots on CEC2013, CEC2014, and CEC2017 test suites
In this section, the convergence speed and stability of the MDE-DPSO algorithm are further verified. The convergence curves for each algorithm are based on the median of 51 runs on the 30D CEC2013 test set, with the results illustrated in Figs. 5, 6 and 7. These convergence plots demonstrate that the MDE-DPSO algorithm achieves better or comparable performance relative to the following algorithms: compared to MPSO, it achieves better or similar performance on \(f_{a2}\)-\(f_{a5}\), \(f_{a7}\)-\(f_{a18}\), \(f_{a20}\), \(f_{a22}\)-\(f_{a24}\), and \(f_{a26}\)-\(f_{a27}\); compared to PSO-sono, it achieves better or similar performance on \(f_{a2}\)-\(f_{a4}\), \(f_{a6}\)-\(f_{a9}\), \(f_{a14}\)-\(f_{a16}\), \(f_{a22}\)-\(f_{a24}\), and \(f_{a26}\)-\(f_{a27}\); compared to EAPSO, it achieves better or similar performance on \(f_{a3}\)-\(f_{a4}\), \(f_{a7}\)-\(f_{a9}\), \(f_{a11}\)-\(f_{a13}\), \(f_{a15}\)-\(f_{a18}\), \(f_{a20}\), \(f_{a23}\)-\(f_{a24}\), and \(f_{a26}\)-\(f_{a27}\); compared to PSO-HBF, it achieves better or similar performance on \(f_{a2}\)-\(f_{a4}\), \(f_{a7}\)-\(f_{a10}\), \(f_{a12}\)-\(f_{a13}\), \(f_{a15}\), \(f_{a18}\), \(f_{a20}\), and \(f_{a23}\)-\(f_{a28}\); compared to ACEPSO, it achieves better or similar performance on \(f_{a2}\)-\(f_{a4}\), \(f_{a7}\)-\(f_{a10}\), \(f_{a12}\)-\(f_{a13}\), \(f_{a16}\), \(f_{a20}\), \(f_{a24}\), and \(f_{a26}\)-\(f_{a27}\); compared to CO, it achieves better or similar performance on \(f_{a3}\)-\(f_{a4}\), \(f_{a7}\)-\(f_{a10}\), \(f_{a12}\)-\(f_{a13}\), \(f_{a15}\)-\(f_{a16}\), \(f_{a18}\), \(f_{a20}\), and \(f_{a23}\)-\(f_{a28}\); compared to HBA, it achieves better or similar performance across all benchmark functions, \(f_{a1}\)-\(f_{a28}\); compared to ARO, it achieves better or similar performance on \(f_{a3}\)-\(f_{a4}\), \(f_{a7}\)-\(f_{a10}\), \(f_{a12}\)-\(f_{a13}\), \(f_{a15}\)-\(f_{a16}\), \(f_{a18}\), \(f_{a20}\), \(f_{a23}\)-\(f_{a24}\), and \(f_{a26}\)-\(f_{a27}\); compared to OMA, it achieves better or similar performance on \(f_{a2}\)-\(f_{a20}\), and \(f_{a22}\)-\(f_{a28}\); compared to EDO, it achieves better or similar performance on \(f_{a1}\), \(f_{a3}\)-\(f_{a24}\), and \(f_{a26}\)-\(f_{a28}\); and compared to WOA-LFDE, it achieves better or similar performance on \(f_{a3}\)-\(f_{a4}\), \(f_{a7}\)-\(f_{a20}\), and \(f_{a22}\)-\(f_{a28}\). Additionally, these results are summarized in Table 27, which highlights the benchmark functions where our algorithm outperforms or matches the best performance compared to the other algorithms. After the convergence plots, we have included box plots for some of the test functions. Box plots, also known as box-and-line plots, are often used to represent the consistency of the distribution between data. The narrower the box corresponding to the algorithm, the more stable the algorithm is and the better the performance. In the block diagrams in this paper, the boxes represent the middle 50 per cent range of the data, the black line represents the median, and the circles represent outliers, which indicate that the data are far from the main data distribution. The black dashed line represents the whiskers, showing the overall range of the data distribution. It is obvious from Figs. 8, 9 and 10 that MDE-DPSO has narrower boxes on most of the benchmark functions, and the box plots are all lower and do not have more outliers, indicating that the MDE-DPSO algorithm has good stability.
Convergence comparison on \(f_{a1}\) and \(f_{a12}\) using the median of 51 runs on the 30D CEC2013 test set.
Convergence comparison on \(f_{a13}\) and \(f_{a24}\) using the median of 51 runs on the 30D CEC2013 test set.
Convergence comparison on \(f_{a25}\) and \(f_{a28}\) using the median of 51 runs on the 30D CEC2013 test set.
From Figs. 5, 6, and 7 we can also see that MDE-DPSO has faster convergence speeds for different types of test functions in the 30D optimization problems. For single-peak (\(f_{a3}, f_{a4}\)), MDE-DPSO achieves better accuracy compared to other algorithms. For multi-peak (\(f_{a7}, f_{a8}, f_{a9}, f_{a20}\)), MDE-DPSO shows superior convergence accuracy over other algorithms, especially on \(f_{a7}\) and \(f_{a9}\), where MDE-DPSO quickly escapes local optima, benefiting from the powerful effects of the new dynamic strategy and mutation crossover operator. For combinatorial functions (\(f_{a24}, f_{a27}\)), MDE-DPSO not only achieves a fast convergence rate but also attains high accuracy.
Performance comparison of algorithms on \(f_{a2}\) and \(f_{a4}\) using box plots on the 30D CEC2013 test set.
Performance comparison of algorithms on \(f_{a8}\), \(f_{a9}\), \(f_{a11}\), \(f_{a12}\), \(f_{a13}\), and \(f_{a17}\) using box plots on the 30D CEC2013 test set.
Performance comparison of algorithms on \(f_{a18}\), \(f_{a21}\), \(f_{a22}\), \(f_{a24}\), \(f_{a27}\), and \(f_{a28}\) using box plots on the 30D CEC2013 test set.
Convergence curves and box plots on CEC2022 test suite
Similarly, we also validated the convergence speed and stability of the MDE-DPSO algorithm on the CEC2022 test suite. The convergence curves for each algorithm are based on the median of 51 runs on the 20D CEC2022 test suite, with the results illustrated in Fig. 11. These convergence plots demonstrate that the MDE-DPSO algorithm achieves better or comparable performance relative to the following algorithms: compared to JADE, it achieves better or similar performance on \(f_{d1}\)-\(f_{d2}\), \(f_{d4}\), \(f_{d6}\)-\(f_{d10}\), and \(f_{d12}\); compared to CWDEPSO, it achieves better or similar performance on \(f_{d2}\)-\(f_{d5}\), \(f_{d7}\), \(f_{d9}\)-\(f_{d10}\), and \(f_{d12}\); compared to DFPSO, it achieves better or similar performance on \(f_{d1}\)-\(f_{d12}\); compared to SQPPSO-sono, it achieves better or similar performance on \(f_{d2}\)-\(f_{d5}\), \(f_{d7}\), \(f_{d9}\)-\(f_{d10}\), and \(f_{d12}\). Similarly, we summarise these results in Table 28. Following the convergence plots, we have also included box plots of some of the test functions on the CEC2022 test suite. As can be seen in Figs. 12 and 13, the MDE-DPSO algorithm remains very stable and robust on most functions on the new test set.
Convergence comparison on \(f_{d1}\) and \(f_{d12}\) using the median of 51 runs on the 20D CEC2022 test set.
From Fig. 11 we can also see that MDE-DPSO achieves higher accuracy on half of the functions (\(f_{d2}\), \(f_{a4}\), \(f_{a7}\), \(f_{a9}\), \(f_{10}\), \(f_{d12}\)). Notably, on the combinatorial functions (\(f_{d9}\), \(f_{d10}\), \(f_{d12}\)), the MDE-DPSO algorithm successfully escapes from the local optimum after only a few iterations, and quickly finds a region close to the global optimum. This result shows that the design of the dynamic strategies and the mutation crossover operator greatly enhances the exploration capability of MDE-DPSO in complex search spaces.
Performance comparison of algorithms on \(f_{d1}\), \(f_{d2}\), \(f_{d4}\), \(f_{d5}\), \(f_{d6}\), and \(f_{d8}\) using box plots on the 20D CEC2022 test set.
Performance comparison of algorithms on \(f_{d11}\) and \(f_{d12}\) using box plots on the 20D CEC2022 test set.
Ablation experiment
In this section, we validate each module of the algorithm. Specifically, eight variants are included: (1) a parameter tuning scheme using a linear-decreasing inertia weight and constant acceleration coefficients (denoted as MDE-DPSO-1); (2) a parameter tuning scheme using a linear-decreasing inertia weight with a sine-cosine acceleration factor (denoted as MDE-DPSO-2); (3) a parameter tuning scheme using a cosine-decreasing inertia weight with constant acceleration coefficients of 2 (denoted as MDE-DPSO-3); (4) a conventional velocity approach (denoted as MDE-DPSO-4); (5) a velocity update approach with a center nearest particle (denoted as MDE-DPSO-5); (6) a version without the mutation crossover operator (denoted as MDE-DPSO-6); (7) a mutation crossover operator strategy using only the DE/rand/1 strategy (denoted as MDE-DPSO-7); and (8) a mutation crossover operator strategy using only the DE/current-to-pbest/1 strategy (denoted as MDE-DPSO-8). It is worth noting that all the eight variants of the MDE-DPSO algorithm proposed in this paper are modifications of the original algorithm, which are only adapted for specific strategies or parameters, while all other parts remain unchanged. We compare these variants with the full MDE-DPSO algorithm, and the experimental results are shown in Tables 29, 30 and 31. The best values are shown in bold. As can be seen from Tables 29, 30 and 31, the performance of MDE-DPSO is improved by 19 compared to MDE-DPSO-1, indicating that the new dynamic parameter adjustment strategy effectively supports the particles to adjust their searching ability at different stages. The performance of MDE-DPSO is improved by 13 and 20 compared with MDE-DPSO-2 and MDE-DPSO-3, respectively, indicating that relying solely on the sine-cosine acceleration factor or the cosine-decreasing inertia weight leads to a significant degradation of the performance; a single parameter adjustment strategy is not sufficient to provide the optimal search capability. Further comparisons with MDE-DPSO-4 and MDE-DPSO-5 show that the performance of MDE-DPSO improves by 17 and 15, respectively, suggesting that the combination of the center nearest particle and the perturbation term helps the algorithm to improve the global search capability and convergence speed. The combination of the center nearest particle, which contains valuable solution information through which the optimal solution can be converged by more efficient particles, and the perturbation term, which provides the algorithm with a certain degree of randomness and helps the particles to explore new regions of the solution space, improves the overall performance of the algorithm. Compared with MDE-DPSO-6, MDE-DPSO-7, and MDE-DPSO-8, the performance of MDE-DPSO is improved by 19, 14, and 20, respectively, which suggests that the flexibility of switching the mutation strategy in the mutation crossover operator achieves a better performance than not using the mutation crossover operator or using only a single mutation strategy. Further comparative analyses of the multi-peak and combinatorial functions show that the performance of MDE-DPSO improves by a factor of 16, 12, and 15 compared to MDE-DPSO-6, MDE-DPSO-7, and MDE-DPSO-8, which are more than half of the evaluated functions. This result further confirms that the introduction of mutation crossover operator with two mutation strategies in PSO enhances the exploration of particles in complex search spaces and effectively maintains the diversity of the population. In conclusion, the absence of any strategy negatively impacts the algorithm’s performance to varying degrees.
Parameter settings
In this section, we analyze the algorithm parameters Nar and \(limit\_num\). The former holds a collection of high-quality solutions found in previous iterations, allowing them to be utilized in subsequent iterations to help the algorithm escape local optima and enhance population diversity. The latter tracks the improvement of each particle in the population, enabling the application of different mutation strategies accordingly. In each test, we varied only one parameter while keeping the others at their default values. For the parameter Nar, we tested four different values: 25, 50, 75, and 100. As shown in Table 32, the best results (in bold) are obtained when \(Nar=100\), with optimal values obtained on 12 functions. This suggests that increasing Nar allows the algorithm to retain more high-quality solutions, which is particularly beneficial for maintaining diversity during the optimization process and avoiding premature convergence. For the parameter \(limit\_num\), we tested six different values: 5, 10, 15, 20, 25, and 30. Increasing \(limit\_num\) means that particles switch to different mutation strategies less frequently, which may cause them to stagnate around local optima for longer periods, potentially preventing them from fully utilizing the stochastic mutation strategy to expand the search space. Conversely, decreasing \(limit\_num\) may cause particles to enter the “lazy” state earlier, potentially enhancing the algorithm’s global exploration capability but also possibly weakening the fine-grained exploitation of local optima. Therefore, selecting an appropriate value is crucial to ensure a balance between global exploration and local exploitation. As shown in Table 33, the alternating mutation strategy performs best when \(limit\_num=10\), providing higher optimization accuracy on most multi-peak and combinatorial functions, outperforming other parameter configurations. This result suggests that \(limit\_num=10\) is a reasonable switching frequency that effectively balances global exploration with local exploitation.
Algorithm time complexity
In this section, we also perform a time complexity test of the proposed MDE-DPSO algorithm and compare it with all PSO variants. The time complexity is evaluated according to the recommendations of the CEC2013 test set for 30D optimization, and the results are shown in Table 34. Specifically, \(T_0\) denotes the time consumed for the basic arithmetic operations recommended by the CEC2013 competition guidelines, and \(T_0\) is the time obtained by calculating the following statements:
for \(i = 1:1000000\)
\(x = (double)i + 5.5; \, x = x + x; \, x = x./2; \, x = x \times x;\)
\(x = \sqrt{x}; \, x = \log (x); \, x = \exp (x); \, y = x / x;\)
end
\(T_1\) denotes the time required for 200000 function evaluations of the 14th benchmark function of the 30D CEC2013 test set, and \(T_2\) reflects the total time consumed to optimize the \(f_{14}\) function. We run 21 times to get the average \(\bar{T_1}\) and \(\bar{T_2}\), and the ratio \(\frac{\bar{T_2}-\bar{T_1}}{T_0}\) is used to evaluate the time complexity of each algorithm. From the results, it can be seen that the MDE-DPSO algorithm has the lowest computational complexity among all the PSO variants, followed by SQPPSO-sono. This suggests that MDE-DPSO achieves more efficient exploration and exploitation of the solution space by employing dynamic strategies as well as mutation crossover operator, which significantly reduce the running time on complex problems.
Conclusion
In this paper, we propose a hybrid differential evolutionary particle swarm optimization algorithm based on dynamic strategies (MDE-DPSO). MDE-DPSO employs a dynamic and novel parameter adjustment strategy and velocity update strategy to optimise the search range and direction of particles. To further prevent particles from stagnating in local optima, MDE-DPSO introduces a mutation crossover operator that combines two mutation strategies to generate diverse candidate solutions. MDE-DPSO outperforms fifteen comparison algorithms on most benchmark functions in different dimensions of the CEC2013, CEC2014, CEC2017, and CEC2022 test suites. Future research will explore the application potential of the MDE-DPSO algorithm in addressing complex real-world challenges, including fire evacuation path planning.
Data availability
The datasets used and/or analysed during the current study available from the corresponding author on reasonable request.
References
Bozorg-Haddad, O., Solgi, M. & Loáiciga, H. A. H. A. Meta-heuristic and evolutionary algorithms for engineering optimization (Wiley, 2017).
Okoji, A. I., Okoji, C. N. & Awarun, O. S. Performance evaluation of artificial intelligence with particle swarm optimization (PSO) to predict treatment water plant DBPs (haloacetic acids). Chemosphere 344, 140238 (2023).
Priyadarshi, N., Padmanaban, S., Maroti, P. K. & Sharma, A. An extensive practical investigation of FPSO-based MPPT for grid integrated PV system under variable operating conditions with anti-islanding protection. IEEE Syst. J. 13, 1861–1871 (2018).
Zeng, N., Zhang, H., Liu, W., Liang, J. & Alsaadi, F. E. A switching delayed PSO optimized extreme learning machine for short-term load forecasting. Neurocomputing 240, 175–182 (2017).
Hu, G., Zheng, Y., Houssein, E. H. & Wei, G. DRPSO: A multi-strategy fusion particle swarm optimization algorithm with a replacement mechanisms for colon cancer pathology image segmentation. Comput. Biol. Med. 178, 108780 (2024).
Iliyasu, A. M., Benselama, A. S., Bagaudinovna, D. K., Roshani, G. H. & Salama, A. S. Using particle swarm optimization and artificial intelligence to select the appropriate characteristics to determine volume fraction in two-phase flows. Fractal Fract. 7, 283 (2023).
Mazhoud, I., Hadj-Hamou, K., Bigeon, J. & Joyeux, P. Particle swarm optimization for solving engineering problems: A new constraint-handling mechanism. Eng. Appl. Artif. Intell. 26, 1263–1273 (2013).
Kirkpatrick, S., Gelatt, C. D. Jr. & Vecchi, M. P. Optimization by simulated annealing. Science 220, 671–680 (1983).
Glover, F. Future paths for integer programming and links to artificial intelligence. Comput. Oper. Res. 13, 533–549 (1986).
Rajeev, S. & Krishnamoorthy, C. Discrete optimization of structures using genetic algorithms. J. Struct. Eng. 118, 1233–1250 (1992).
Storn, R. & Price, K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 11, 341–359 (1997).
Deb, K., Pratap, A., Agarwal, S. & Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 6, 182–197 (2002).
Meng, Z. & Chen, Y. Differential evolution with exponential crossover can be also competitive on numerical optimization. Appl. Soft Comput. 146, 110750 (2023).
Meng, Z. Dimension improvements based adaptation of control parameters in differential evolution: A fitness-value-independent approach. Expert Syst. Appl. 223, 119848 (2023).
Eberhart, R. & Kennedy, J. Particle swarm optimization. Proc. IEEE Int. Conf. Neural Netw. 4, 1942–1948 (1995).
Zhao, S., Zhang, T., Ma, S. & Wang, M. Sea-horse optimizer: A novel nature-inspired meta-heuristic for global optimization problems. Appl. Intell. 53, 11833–11860 (2023).
Mirjalili, S., Mirjalili, S. M. & Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 69, 46–61 (2014).
Abdel-Basset, M., Mohamed, R., Jameel, M. & Abouhawwash, M. Spider wasp optimizer: A novel meta-heuristic optimization algorithm. Artif. Intell. Rev. 56, 11675–11738 (2023).
Cheng, M.-Y. & Sholeh, M. N. Optical microscope algorithm: A new metaheuristic inspired by microscope magnification for solving engineering optimization problems. Knowl.-Based Syst. 279, 110939 (2023).
Abdel-Basset, M., Mohamed, R., Azeem, S. A. A., Jameel, M. & Abouhawwash, M. Kepler optimization algorithm: A new metaheuristic algorithm inspired by Kepler’s laws of planetary motion. Knowl.-Based Syst. 268, 110454 (2023).
Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl.-Based Syst. 96, 120–133 (2016).
Abdel-Basset, M., El-Shahat, D., Jameel, M. & Abouhawwash, M. Exponential distribution optimizer (EDO): A novel math-inspired algorithm for global optimization and engineering problems. Artif. Intell. Rev. 56, 9329–9400 (2023).
Liu, H., Zhang, X.-W. & Tu, L.-P. A modified particle swarm optimization using adaptive strategy. Expert Syst. Appl. 152, 113353 (2020).
Meng, Z., Zhong, Y., Mao, G. & Liang, Y. PSO-SONO: A novel PSO variant for single-objective numerical optimization. Inf. Sci. 586, 176–191 (2022).
Chen, Y., Li, L., Peng, H., Xiao, J. & Wu, Q. Dynamic multi-swarm differential learning particle swarm optimizer. Swarm Evol. Comput. 39, 209–221 (2018).
Lin, M., Wang, Z. & Zheng, W. Hybrid particle swarm-differential evolution algorithm and its engineering applications. Soft. Comput. 27, 16983–17010 (2023).
Lin, A., Liu, D., Li, Z., Hasanien, H. M. & Shi, Y. Heterogeneous differential evolution particle swarm optimization with local search. Complex Intell. Syst. 9, 6905–6925 (2023).
Liang, J. J., Qin, A. K., Suganthan, P. N. & Baskar, S. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions. IEEE Trans. Evol. Comput. 10, 281–295 (2006).
Wang, H., Wu, Z., Rahnamayan, S., Liu, Y. & Ventresca, M. Enhancing particle swarm optimization using generalized opposition-based learning. Inf. Sci. 181, 4699–4714 (2011).
Li, H., Li, J., Wu, P., You, Y. & Zeng, N. A ranking-system-based switching particle swarm optimizer with dynamic learning strategies. Neurocomputing 494, 356–367 (2022).
Li, T., Shi, J., Deng, W. & Hu, Z. Pyramid particle swarm optimization with novel strategies of competition and cooperation. Appl. Soft Comput. 121, 108731 (2022).
Wang, Z., Chen, Y., Ding, S., Liang, D. & He, H. A novel particle swarm optimization algorithm with lévy flight and orthogonal learning. Swarm Evol. Comput. 75, 101207 (2022).
Duan, Y. et al. CAPSO: Chaos adaptive particle swarm optimization algorithm. IEEE Access 10, 29393–29405 (2022).
Tian, D., Zhao, X. & Shi, Z. Chaotic particle swarm optimization with sigmoid-based acceleration coefficients for numerical function optimization. Swarm Evol. Comput. 51, 100573 (2019).
Wolpert, D. H. & Macready, W. G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1, 67–82 (1997).
Liu, H., Cai, Z. & Wang, Y. Hybridizing particle swarm optimization with differential evolution for constrained numerical and engineering optimization. Appl. Soft Comput. 10, 629–640 (2010).
Sayah, S. & Hamouda, A. A hybrid differential evolution algorithm based on particle swarm optimization for nonconvex economic dispatch problems. Appl. Soft Comput. 13, 1608–1619 (2013).
Zhai, S. & Jiang, T. A new sense-through-foliage target recognition method based on hybrid differential evolution and self-adaptive particle swarm optimization-based support vector machine. Neurocomputing 149, 573–584 (2015).
Melton, R. G. Differential evolution/particle swarm optimizer for constrained slew maneuvers. Acta Astronaut. 148, 246–259 (2018).
Mohammadi, B., Guan, Y., Moazenzadeh, R. & Safari, M. J. S. Implementation of hybrid particle swarm optimization-differential evolution algorithms coupled with multi-layer perceptron for suspended sediment load estimation. CATENA 198, 105024 (2021).
Dadvar, M., Navidi, H., Javadi, H. H. S. & Mirzarezaee, M. A cooperative approach for combining particle swarm optimization and differential evolution algorithms to solve single-objective optimization problems. Appl. Intell. 52, 4089–4108 (2022).
Yuan, Q., Sun, R. & Du, X. Path planning of mobile robots based on an improved particle swarm optimization algorithm. Processes 11, 26 (2022).
Wang, J., Wang, X., Li, X. & Yi, J. A hybrid particle swarm optimization algorithm with dynamic adjustment of inertia weight based on a new feature selection method to optimize SVM parameters. Entropy 25, 531 (2023).
Shi, Y. & Eberhart, R. C. Empirical study of particle swarm optimization. In Proceedings of the 1999 congress on evolutionary computation-CEC99 (Cat. No. 99TH8406) 3, 1945–1950 (1999).
Li, J. & Meng, Z. Global opposition learning and diversity enhancement based differential evolution with exponential crossover for numerical optimization. Swarm Evol. Comput. 87, 101577 (2024).
Zhang, J. & Sanderson, A. C. JADE: Adaptive differential evolution with optional external archive. IEEE Trans. Evol. Comput. 13, 945–958 (2009).
Zhang, Y. Elite archives-driven particle swarm optimization for large scale numerical optimization and its engineering applications. Swarm Evol. Comput. 76, 101212 (2023).
Zare, M. et al. A modified particle swarm optimization algorithm with enhanced search quality and population using hummingbird flight patterns. Decis. Anal. J. 7, 100251 (2023).
Hu, G., Cheng, M., Sheng, G. & Wei, G. ACEPSO: A multiple adaptive co-evolved particle swarm optimization for solving engineering problems. Adv. Eng. Inform. 61, 102516 (2024).
Li, Q. & Ma, Z. A hybrid dynamic probability mutation particle swarm optimization for engineering structure design. Mob. Inf. Syst. 2021, 6648650 (2021).
Rezaei, F. & Safavi, H. R. Sustainable conjunctive water use modeling using dual fitness particle swarm optimization algorithm. Water Resour. Manag. 36, 989–1006 (2022).
Hong, L., Yu, X., Tao, G., Özcan, E. & Woodward, J. A sequential quadratic programming based strategy for particle swarm optimization on single-objective numerical optimization. Complex Intell. Syst. 10, 2421–2443 (2024).
Akbari, M. A., Zare, M., Azizipanah-Abarghooee, R., Mirjalili, S. & Deriche, M. The cheetah optimizer: A nature-inspired metaheuristic algorithm for large-scale optimization problems. Sci. Rep. 12, 10953 (2022).
Hashim, F. A., Houssein, E. H., Hussain, K., Mabrouk, M. S. & Al-Atabany, W. Honey badger algorithm: New metaheuristic algorithm for solving optimization problems. Math. Comput. Simul. 192, 84–110 (2022).
Wang, L., Cao, Q., Zhang, Z., Mirjalili, S. & Zhao, W. Artificial rabbits optimization: A new bio-inspired meta-heuristic algorithm for solving engineering optimization problems. Eng. Appl. Artif. Intell. 114, 105082 (2022).
Liu, M., Yao, X. & Li, Y. Hybrid whale optimization algorithm enhanced with lévy flight and differential evolution for job shop scheduling problems. Appl. Soft Comput. 87, 105954 (2020).
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. U1805264), the Fujian Provincial Department of Science and Technology Industrial Technology Development and Application Plan Guiding Project (Grant Nos. 2022Y0077, 2023Y6004), the Fujian Provincial Department of Science and Technology Major Special Project (Grant No. 2022YZ040011), and the 2024 Fujian Provincial Department of Science and Technology’s Science and Technology Promotion Police Research Special Project (Grant Nos. 2024YZ040001, 2024Y0072).
Author information
Authors and Affiliations
Contributions
H.X.: Propose ideas and project funding, complete the experimental part and review and edit the thesis. Q.D.: Complete the experimental part and be responsible for the first draft. Z.Z.: Review and edit the first draft. S.L.: Review and edit the first draft.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Xu, H., Deng, Q., Zhang, Z. et al. A hybrid differential evolution particle swarm optimization algorithm based on dynamic strategies. Sci Rep 15, 4518 (2025). https://doi.org/10.1038/s41598-024-82648-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-82648-5
