Introduction

Operational maintenance and safety have gained importance in the last few decades due to the dramatic increase in global photovoltaic (PV) capacity. Photovoltaic arrays are susceptible to a range of unforeseen malfunctions resulting from the unpredictable conditions in which they operate outside. These malfunctions can lead to significant power loss, irreversible damage to the modules, and, in extreme cases, even fires1,2, Nevertheless, PV modules are vulnerable to extreme environmental conditions such as humidity, snow, sand, dirt, and wetness due to their exterior placement. They can also potentially sustain damage during transit or installation3.

Fault diagnosis is essential for ensuring the reliability, safety, and efficiency of solar systems. In the absence of effective fault identification, uncleared defects in photovoltaic arrays not only result in power losses4, but also challenge conventional protection devices based on NEC, IEC, and UL standards. These devices struggle to detect and differentiate faults in the DC portion of the PV system (PVS) due to the low fault current rating, Maximum Power Point Tracking (MPPT) availability, nonlinear characteristics of PV systems, and their dependence on radiation5.

Generally, these protection devices fail to detect faults in the PV system due to low fault current rates, MPPTs, the nonlinear nature of PV, and high reliance on solar input. Complete system degradation can also occur despite the presence of protective mechanisms6,7.

Consequently, in recent years, several research institutes have begun studying fault detection technologies in PV systems8, presently, numerous academics have conducted studies on the detection and diagnosis of problems in PV systems. This research can be categorized into two distinct groups: threshold techniques and intelligent algorithms9, fault diagnosis via the threshold approach involves measuring many electrical parameters, including output power, voltage, and current. These values are then contrasted with pre-established thresholds to ascertain the existence and characteristics of each imperfection10.

The I–V curve can be utilized, either partially or whole, for the purpose of fault diagnostics. During a test, the decision-making process focuses on a limited number of specific factors, such as open-circuit voltage (Voc), short-circuit current (Isc), and peak potential power (Pmpp). Drawbacks of this technique encompass limited detection mistakes and a heightened susceptibility to environmental fluctuations11. Nevertheless, the I-V curve is extensively discussed because it provides valuable information regarding the condition of the PV module12, however, to acquire this curve, a tracer is required, and production must be temporarily halted during measurement. Providing an I-V tracer at an affordable price while minimizing manufacturing losses is a difficult task13.

Recent studies have highlighted advancements in fault feature extraction methods for bearing systems, particularly under time-varying speed conditions14. Zhao, Cui, and Liu introduced a novel frequency matching demodulation transform to address weak fault features in such environments15. Additionally, a multiple-medium AC-port power electronic transformer was introduced by Zhang et al., providing new solutions for power systems16. The adaptive synchronous demodulation transform method, as proposed by Miaofen et al., further enhances the analysis of multicomponent signals for machinery fault diagnostics17. Wang and colleagues developed a fault characteristic order (FCO) analysis for rolling element bearings, significantly improving fault diagnosis18. Wang et al. also introduced a SKRgram-based demodulation technique, which proved effective for planet bearing fault detection19. In the field of permanent magnet synchronous machine systems, Hang and colleagues improved fault diagnosis methods by applying lightweight multisource information data layer fusion20. Robust diagnosis of partial demagnetization faults under complex conditions was advanced by He et al., who leveraged radial air-gap flux density measurements21. Meng et al. proposed a novel approach to revolutionize photovoltaic consumption and electric vehicle charging in residential distribution systems22. Yang et al. presented a framework based on a parallel convolutional neural network and bidirectional gated recurrent unit for structural damage detection23. Finally, Li et al. introduced a deep dynamic high-order graph convolutional network for diagnosing wear faults in hydrodynamic mechanical seals24.

PV defect detection models are established using fuzzy classifiers, artificial neural networks, the multiclass adaptive neuro-fuzzy classifier (MC-NFC), and the kernel-based extreme learning machine algorithm (KELM). While AI technologies can enhance fault classification accuracy to a certain degree, only a limited number of researchers have made efforts to validate the generalization capability of AI fault diagnosis algorithms or AI training models. The variability in output voltages and currents in PV modules is mostly due to their susceptibility to changes in irradiance and temperatures. Additionally, the installation environments of a PVS might vary significantly25.

The accuracy of PV fault detection can be significantly influenced by the variability of derived indicators, particularly if proper normalization is not applied. This variability is often due to the differing Standard Test Condition (STC) characteristics of PV modules. In one approach, solar irradiance and PV output power were utilized as inputs to an artificial neural network (ANN) for defect detection in PV systems26,27, faults were detected by a radial basis function neural network. Additionally, several combined fault detection methods were merged, and a new combination of evidence was developed to improve diagnostic accuracy28, while another method employed a radial basis function neural network to detect faults, improving detection accuracy29.

Additionally, several fault detection techniques were combined, and a novel evidence fusion strategy was developed to enhance diagnostic precision30. A prototype system based on a single diode model was constructed to simulate PV array characteristics, with a support vector machine (SVM) used to evaluate the residual output power of the simulation model for fault detection31, Another approach incorporated experimental data into a PV model using the K-nearest neighbor (KNN) algorithm for fault identification, leveraging operating conditions and weather data to compare real and simulated data32, Furthermore, artificial neural networks were applied to enhance fault detection by recognizing key patterns in the data. However, while these methods show promise, they often lack detailed information about PV faults, especially when multiple faults occur simultaneously. This challenge underscores the need for more comprehensive approaches to fault detection in distributed PV systems33.

Recent studies have utilized I–V curves as input data in combination with AI algorithms to enhance diagnostic capabilities. For instance, Honglu Zhu and colleagues34 applied the output characteristics of photovoltaic arrays and the distribution of electrical eigenvectors under fault conditions with a probabilistic neural network model. However, their approach was limited by the use of direct I–V vectors, which did not contribute significant improvements. In contrast, Mahmoud Dhimish and his team35 proposed incorporating new vectors within a fuzzy classification system, but their method remained largely theoretical. Nguyen Thi Ngoc Trinh and colleagues36 also used I–V curves as input, combining Principal Component Analysis (PCA) with Support Vector Machines (SVM), though concerns arose that PCA might reduce the comprehensiveness of the information by oversimplifying the I–V curve features. Baojie Li and his team37 advanced the research by converting I–V curve features into images using Gramian Angular Difference Fields (GADF) and integrating them with an Artificial Neural Network (ANN). However, their study primarily focused on identifying the most appropriate features for the algorithms, while overlooking the selection of critical features within the vectors that could further enhance the efficiency of photovoltaic system diagnosis. This highlights the need for a more comprehensive approach that integrates the strengths of AI methods with improved feature selection to boost diagnostic accuracy.

This paper addresses the limitations of previous methodologies by introducing a novel approach that integrates I–V curves as vectors with advanced AI algorithms. The proposed model employs sophisticated classification algorithms alongside an enhanced optimization algorithm, specifically the Harris Hawks Optimization (HHO) that has never been used before in PV system diagnosis, to identify and select the most critical features within the I–V curve data. By preserving the essential diagnostic information, the model ensures high accuracy in fault diagnosis. HHO plays a key role in filtering the I–V curve features, enabling the model to focus solely on the most relevant information for effective classification. This synergy between classification and optimization algorithms creates a robust and comprehensive framework for diagnosing PV system conditions. Not only does this approach overcome the shortcomings of previous methods, but it also demonstrates superior performance, as evidenced by experimental test results. The proposed framework significantly outperforms existing methodologies, making it a powerful tool for achieving accurate and reliable PV system diagnosis.

The paper is structured as follows: Sect. 2 explores the fundamental principles of photovoltaic systems and their application to system analysis. Section 3 details the development and configuration of the experimental test bench, focusing on implementing a DC/DC buck-boost converter for extracting real-time data. Section 4 provides a comprehensive analysis of PV system faults by examining I-V curve characteristics to monitor system status. Section 5 introduces innovative methodologies for real-time monitoring and fault detection, integrating feature selection with classification algorithms. Section 6 presents a detailed analysis of the results obtained from the proposed AI techniques. The final section summarizes and discusses the key insights and implications of the study, highlighting the efficiency and effectiveness of the proposed strategy.

Theoretical foundations and system analysis applications

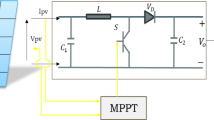
The major power source of the I-V tracer for photovoltaic systems is a solar panel, which is equipped with current and voltage sensors to precisely monitor output characteristics. A DC-DC converter, regulated by a Pulse Width Modulation (PWM) signal, modifies the voltage to align with the load demands. The load refers to the equipment that consumes power38, data from the sensors is collected by a data acquisition system. The TMS320F28379D LaunchPad orchestrates the entire system, ensuring precise control and accurate data collection, as illustrated in Fig. 1.

Fig. 1
figure 1

Proposed Circuit for Extracting Voltage-Current Characteristics Using a DC-DC Buck-Boost Converter.

Full size image

The proposed circuit, illustrated in Fig. 1, integrates a DC-DC Buck-Boost Converter with a carefully designed network of series and parallel resistors that serve as voltage and current sensors. This configuration allows all components to share a common ground, ensuring direct and stable connection to the TMS320f28379d microcontroller.

For voltage measurement, a voltage divider circuit is created by connecting two resistors in parallel across the PV panel’s output. This voltage divider reduces the PV panel’s output voltage to a level compatible with the microcontroller’s input specifications, allowing accurate readings within its analog-to-digital converter (ADC) range.

The current sensor, on the other hand, is configured by placing a precision resistor in series with the PV panel output. Based on Ohm’s law, this series resistor converts the current from the PV panel into a proportional voltage, which the microcontroller can then measure. The values of the series and parallel resistors were selected based on the PV panel’s rated voltage and current to ensure accurate measurements without exceeding the microcontroller’s input limits.

In operation, the TMS320F28379D LaunchPad reads the analog signals from these sensors in real-time, capturing both voltage and current data from the PV panel. This data is processed and transmitted to a monitoring device. The circuit also controls the DC-DC buck-boost converter via Pulse Width Modulation (PWM), which dynamically adjusts the converter’s switching patterns to regulate the output voltage according to varying load demands.

The collected data is then logged into an Excel-based system for further analysis. This allows for efficient diagnostics and optimization of the PV system’s performance, as well as an enhancement of the Maximum Power Point Tracking (MPPT) process. By continuously monitoring the actual operational state of the PV panels, the system can select and implement the most effective MPPT algorithm, further improving overall energy efficiency39.

Modelling of a PV cell

The Single-Diode Model (SDM), depicted in Fig. 2, is a widely used electrical circuit for photovoltaic (PV) cells. It incorporates five key parameters: photocurrent, diode saturation current, ideality factor, series resistance, and shunt resistance40.

Fig. 2
figure 2

Equivalent Circuit of a PV Cell.

Full size image

As shown in Fig. 2, the solar PV device can be represented as an ideal solar cell with a current source (\(\:{I}_{ph}\)) in parallel with the diode41,42. The output current of an ideal solar cell is defined by Eq. (1).

$$\:{I\:=I}_{ph}-\:{I}_{s}\left[exp\left(\frac{q\:\left(\frac{{V}_{pv}}{{N}_{s}}+{I}_{pv}{R}_{s}\:\right)}{nk{T}_{k}}\right)-1\right]-\left(\frac{\frac{{V}_{pv}}{{N}_{s}}+{I}_{pv}{R}_{s}}{{R}_{sh}}\:\right)\:\:\:$$
(1)
$$\:I\:={I}_{ph}-{I}_{d}$$
(2)

where:

\(\:{I}_{ph}\) is the photo-generated current (or light-generated current).

\(\:{I}_{d}\) : the current through the diode.

\(\:{I}_{s}\) : the reverse saturation current of the diode.

\(\:{V}_{pv}\)​: the voltage across the solar cell.

\(\:{N}_{s}\) : the number of series-connected cells.

\(\:{I}_{pv}\)​: the current through the solar cell.

\(\:{R}_{s}\)​: the series resistance of the solar cell.

\(\:n\) : the ideality factor of the diode.

\(\:k\) : the Boltzmann constant.

\(\:{T}_{k}\)​: the temperature in Kelvin.

Buck-boost converter

A buck-boost converter is a type of DC-DC converter that has the ability to increase or decrease the output voltage with respect to the input voltage Similar to how transformers are used in AC circuits, they are used to increase the DC voltage43, the fly-back converter is essentially replaced by a solitary inductor in lieu of a transformer. There are two distinctly different types referred to as buck-boost converters44,45,46,47. DC-DC converters, commonly referred to as choppers, utilize the versatile Buck-Boost converter. This converter can function as either a step-down or step-up converter, depending on its duty cycle, which is denoted as DA. The following diagram illustrates a standard configuration of a Buck-Boost converter circuit48, as illustrated in Fig. 3.

Fig. 3
figure 3

The Circuit Representation of Buck-Boost Converter.

Full size image

Mode I: switch is ON, diode is OFF

Let us denote the duration of the switch being in the on state as TON and the duration of the switch being in the off state as TOFF. We may define the total time period, T, as:

$$\:T={T}_{ON}+{T}_{OFF}$$
(3)

and the switching frequency:

$$\:{f}_{\text{switching\:}}=\frac{1}{T}$$
(4)

Let us now define another term, the duty cycle:

$$\:D=\frac{{T}_{ON}}{T}\:\:$$
(5)

Let’s analyze the Buck Boost converter in steady state operation for this mode using KVL.

$$\:\left\{\begin{array}{l}\:{V}_{in}={V}_{L}\:\:\:\:\:\:\:\:\:\:\:\\\:{V}_{L}=L\frac{d{i}_{L}}{dt}={V}_{in}\\\:\frac{d{i}_{L}}{dt}=\frac{\varDelta\:{i}_{L}}{\varDelta\:t}=\frac{\varDelta\:{i}_{L}}{DT}=\frac{{V}_{\text{in\:}}}{L}\end{array}\right.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$
(6)

Since the switch is closed for a time TON = DT we can say that Δt = DT.

$$\:{\left({\Delta\:}{i}_{L}\right)}_{\text{closed\:}}=\left(\frac{{V}_{in}}{L}\right)DT\:\:\:$$
(7)

When analyzing the Buck-Boost converter, it is important to consider that the inductor current must be continuous. This can be achieved by carefully choosing an acceptable value for the inductor, denoted as L.

In steady state, the current in the inductor increases from a starting value with a positive rate of change until it reaches a maximum value during the ON state, Subsequently, it reverts to the initial value with a negative rate of change. Therefore, the overall change in the inductor’s current throughout an entire cycle is insignificant.

Mode II: switch is OFF, diode is ON

Let us now analyse the Buck Boost converter in steady state operation for Mode II using KVL.

$$\:\left\{\begin{array}{l}\:{V}_{L}={V}_{o}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\\\:{\:V}_{L}=L\frac{d{i}_{L}}{dt}={V}_{o}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\\\:\frac{d{i}_{L}}{dt}=\frac{{\Delta\:}{i}_{L}}{{\Delta\:}t}=\frac{{\Delta\:}{i}_{L}}{(1-D)T}=\frac{{V}_{o}}{L}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\end{array}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\right.$$
(8)

Since the switch is open for a time

$$\:{T}_{OFF}=T-{T}_{ON}=T-DT=(1-D)T\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$
(9)

We can say that

$$\:\left\{\begin{array}{l}\varDelta\:t=(1-D)T\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\\\:{\left({\Delta\:}{i}_{L}\right)}_{\text{open\:}}=\left(\frac{{V}_{o}}{L}\right)\left(1-D\right)T\:\:\:\end{array}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\right.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$
(10)

It is a well-established fact that the net change in the current of an inductor during a whole cycle is zero.

$$\:\left\{\begin{array}{l}{\left({\Delta\:}{\text{i}}_{\text{L}}\right)}_{\text{closed\:}}+{\left({\Delta\:}{\text{i}}_{\text{L}}\right)}_{\text{open\:}}=0\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\\\:\left(\frac{{V}_{o}}{L}\right)\left(1-D\right)T+\left(\frac{{V}_{\text{in\:}}}{L}\right)DT=0\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\\\:\frac{{V}_{o}}{{V}_{\text{in\:}}}=\frac{D}{1-D}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\end{array}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\right.$$
(11)

The range of values ​​for D is from 0 to 1. If the value of D is greater than 0.5, the output power exceeds the input power. Conversely, When the value of D is less than 0.5, the output voltage is less than the input voltage. However, when the value of D is exactly 0.5, the output voltage is equal to the input voltage.

A Fig. 4 for the output voltage as a function of the duty cycle is shown in the figure for different types of DC-DC converters, including Buck, Boost, and Buck-Boost converters49. The ideal curves illustrate the theoretical output voltage without considering losses, while the practical curves account for non-ideal behavior in components such as inductors, capacitors, and semiconductor switches. The Buck-Boost curve starts with the load increasing from zero, and at a duty cycle of around 0.5, the PV panel appears directly connected to the load. Beyond this, the Boost mode maximizes power output, covering all functional points and providing a more accurate VI curve compared to using only Boost or Buck converters.

Fig. 4
figure 4

Dependence of VOUT/ VIN on Duty Cycle in Buck, Boost, and Buck-Boost Converters.

Full size image

Experimental test bench

Figure 5 illustrates an experimental test bench developed for the setup. It includes PV panels that convert solar energy into electrical power, which is then fed into an advanced electronic device for processing and analysis. The device integrates several key components: a transistor (MOSFET) for signal switching, controlled by a gate drive circuit; a capacitor for energy storage and voltage stabilization; and a load representing the system’s energy-consuming element.

Fig. 5
figure 5

Experimental Test Bench for Integrating the PV System and Buck-Boost Converter Controlled by the TMS320F28379D LaunchPad.

Full size image

The core of the device’s control mechanism is the TMS320F28379D LaunchPad, which acts as the real-time control algorithms necessary for fault diagnosis by analysis of I-V curve characteristics The system also includes a series resistance to control current flow, ensuring that circuit safety and stability.

The laptop connected to the instrument acts as a monitoring interface, displaying real-time data, system performance metrics, and analysis results. These interfaces are critical for evaluating power parameters and detecting I-V curve anomalies, thus facilitating proper fault diagnosis The test bench is an example of renewable energy technologies to be integrated into energy management systems that are surprisingly, providing a robust platform for testing and developing fault-finding methods in solar power systems.

Comprehensive analysis of photovoltaic system faults using I-V curve characteristics

The proposed test can monitor the status of the PV system and detect faults in real time through the I-V curve, where emergency changes are detected indicating the status of the PV module. The provided Fig. 6. I-V curves illustrate the effects of various fault conditions in photovoltaic (PV) strings under standard test conditions, such as dust, humidity, partial shading, short-circuit, and PV degradation. Each fault uniquely alters the I-V characteristics, with faults like short-circuit and shading causing steep declines in current and voltage due to the activation of bypass diodes, which prevent damage but reduce power output. Faults like dust and humidity lead to more gradual efficiency losses, while the healthy curve represents ideal PV system performance.

Fig. 6
figure 6

Typical I–V Characteristics of PV Panels Under Different Fault Conditions.

Full size image

The Fig. 7A–H, gives a detailed plot of the I-V curves for each of the photovoltaic (PV) systems under various conditions including optimum operation (healthy), dust accumulation, shadow effects, humidity rise, open circuit, short circuit, and PV degradation .The graph shows the typical I-V curve patterns associated with these conditions, and provides the insight needed to detect and troubleshoot faults and to ensure the efficiency of the solar system. These faults have been extensively studied and documented in other studies11,32, making them important for understanding and improving the performance of the PV system under different environmental conditions and operating conditions.

Fig. 7
figure 7figure 7

Graphical Representation of Experimentally Extracted I–V Characteristics of a Photovoltaic System Under Various Fault Conditions.

Full size image

Fault differences of the PV system

The Fig. 7(A) shows the typical I-V curves of a healthy PV system compared to several fault conditions such as dust, shadows, open circuit, PV degradation and short circuit Each fault exhibits a different characteristic of the I-V curve, as it helps to detect and identify various types of faults.

Healthy

Figure 7(B) shows the I-V curves of a healthy PV system under different irradiation levels. fluency and predictability of the curves reflects the optimal performance of the system, where the increase in radiation is proportional to the increase in current voltage.

Dust

Figure 7(C) shows the impact of dust accumulation on the PV panels. I-V curves below radiation levels show a reduction in current output and obvious distortion, emphasizing the importance of regular maintenance and repair.

Shadow

Figure 7(D) shows the impact of partial shading on the PV panels. The I-V curves show large fluctuations and decreases compared to the healthy condition, which can significantly affect the system performance and power output.

Humidity

Figure 7(E) shows the impact of the humidity intensity on the PV system. The I-V curves are irregular and show decreased efficiency, indicating the need for moisture protection measures.

Open circuit

Figure 7(F) shows the open circuit condition in the PV system. I-V curves exhibit a sharp drop in current, indicating a continuity failure in the circuit, requiring immediate attention.

Short circuit

Figure 7(G) shows the impact of short circuit in PV system. The I-V curves exhibit a significant voltage drop, which emphasizes the need for regular maintenance.

PV degradation

Figure 7(H) shows the impact of degradation of PV panels with time. The I-V curves show a gradual decrease in performance, indicating the importance of timely repair and replacement of old deteriorating components.

Proposed methodology

The proposed method shown in Fig. 8 aims to detect faults in photovoltaic (PV) systems by utilizing a combination of gathering experimental data, extracting relevant features, optimizing feature selection, and employing machine learning algorithms. Here, the method is presented in a comprehensive and sequential manner.

Fig. 8
figure 8

Proposed approach for PV system fault detection.

Full size image

PV panels and external influences

A PV system generates electricity through radiation, converting sunlight into usable energy. The efficiency of this process is directly influenced by the amount of sunlight that reaches the panels.

However, external influences such as shade, dust, humidity, and other environmental factors can reduce the system’s performance, potentially causing defects that limit its effectiveness.

Device and data collection

An I-V curve device measures the current and voltage characteristics of the PV panel, which is crucial for understanding its operation and detecting any faults. The measured I-V curves are collected and stored in a database, with data gathered over an extended period to assess panel performance under various conditions. Once collected, the data is processed in a dedicated environment, where it is cleaned, filtered, normalized, and transformed. This phase includes removing noise, handling missing values, and organizing the data. The final dataset consists of seven PV system cases, each containing 94 samples, totaling 658 samples. For each sample, there are 200 current features and 200 voltage features, resulting in 400 total features (IV). The dataset is organized into a matrix with 658 rows representing samples and 400 columns representing features, structured as matrix [V, I].

Harris Hawks optimization-based feature selection

Harris Hawks optimization (HHO) is a newly developed approach in the field of metaheuristic optimization50,51. It was proposed by Haidari and his colleagues in their publication52, HHO is classified as a population-based algorithm, where a collective of hawks collaboratively hunt for prey using diverse strategies. The Harris hawks undergo two primary phases, namely exploitative and explorative, during which they strategically locate their target, swiftly approach it, and employ a range of attack techniques53. Figure 954 illustrates the several stages of HHO, which will be explained in the next subsections.

Fig. 9
figure 9

The schematic diagram of the HHO algorithm.

Full size image

Exploration phase

HHO employs two tactics during the exploration phase:

$$\:X\left(t+1\right)=\left\{\begin{array}{ll}{\varvec{X}}_{\text{rand\:}}\left(\varvec{t}\right)-{\varvec{r}}_{1}\left|{\varvec{X}}_{\text{rand\:}}\left(\varvec{t}\right)-2{\varvec{r}}_{2}\varvec{X}\left(\varvec{t}\right)\right|&\:\varvec{q}\ge\:0.5\\\:\left({\varvec{X}}_{\text{rabbit\:}}\left(\varvec{t}\right)-{\varvec{X}}_{\varvec{m}}\left(\varvec{t}\right)\right)-{\varvec{r}}_{3}\left(\varvec{L}\varvec{B}+{\varvec{r}}_{4}(\varvec{U}\varvec{B}-\varvec{L}\varvec{B})\right)&\:\varvec{q}<0.5\end{array}\right.\:$$
(12)

X represent the position of the hawk, t represent the number of iterations, Xrand indicate the randomly selected hawk from the population, Xrabbit denote the position of the rabbit, r1,r2,r3,r4,, and q represent random numbers between 0 and 1, UB and LB represent the upper and lower bounds of variables, and Xm(t) represents the average position of hawks. Xm(t) is calculated as follows:

$$\:{X}_{m}\left(t\right)=\frac{1}{N}\sum\:_{i=1}^{N}\:{X}_{i}\left(t\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$
(13)

where N indicates the population size.

Transition from exploration to exploitation

The shift from the exploration phase to the exploitation phase in the search process is mostly determined by the escaping energy coefficient (E), which is calculated using the following formula:

$$\:E=2{E}_{0}\left(1-\frac{t}{T}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$
(14)

where \(\:{E}_{0}\) represents a random number within the range of -1 to 1, whereas T signifies the maximum number of iterations.

Exploitation phase

HHO uses the following strategies to simulate the exploitation process.

Soft Besiege: if the value of r is greater than or equal to 0.5 and the absolute value of E is greater than or equal to 0.5, then the rabbit still possesses sufficient energy to flee. Therefore, the hawks quietly surround the rabbit in order to deplete its energy more prior to executing a sudden attack. The concept of soft besiege can be expressed mathematically in the following manner:

$$\:X\left( {t + 1} \right) = \Delta \:X\left( t \right) - E\left| {JX_{{{\text{rabbit}}\:}} \left( t \right) - X\left( t \right)} \right|\:$$
(15)
$$\:{\Delta\:}X\left(t\right)={X}_{\text{rabbit\:}}\left(t\right)-X\left(t\right)\:\:$$
(16)

Hard Besiege: if the value of r is equal to or greater than 0.5 and the absolute value of E is less than 0.5, then the rabbit is weary and its likelihood of escaping is low. In this situation, the hawk circles the rabbit with minimal movement in order to carry out a sudden and decisive surprise strike. The subsequent position of the hawk is determined by the following Eq. 

$$\:X\left(t+1\right)={X}_{\text{rabbit\:}}\left(t\right)-E\left|{\Delta\:}X\left(t\right)\right|\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$
(17)

Soft besiege with progressive rapid dives: When the value of r is less than 0.5 and the absolute value of E is greater than or equal to 0.5, the amount of escaping energy is sufficient and the prey has an opportunity to escape. This phase consists of two phases. The initial step is carried out using the subsequent equation:

$$\:Y={X}_{\text{rabbit\:}}\left(t\right)-E\left|{X}_{\text{rabbit\:}}\left(t\right)-X\left(t\right)\right|\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$
(18)

Following the completion of the initial phase, if the locations of the hawks have not been enhanced, the subsequent step, which utilizes the L´evy flight operator, is done as follows:

$$\:Z=Y+S\times\:LF\left(D\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$
(19)

D represent the dimension of the problem, S represents a random vector with a size1 × D, and LF is the L´evy flight function, which is calculated as follows:

$$\:LF\left(x\right)=0.01\times\:\frac{u\times\:\sigma\:}{|v{|}^{\frac{1}{\beta\:}}},\sigma\:={\left(\frac{{\Gamma\:}\left(1+\beta\:\right)\times\:\text{sin}\left(\frac{\pi\:\beta\:}{2}\right)}{{\Gamma\:}\left(\frac{1+\beta\:}{2}\right)\times\:\beta\:\times\:{2}^{\left(\frac{\beta\:-1}{2}\right)}}\right)}^{\frac{1}{\beta\:}}\:\:\:\:\:\:$$
(20)

Where u and v represent the random parameters of LF, and β is assigned a value of 1.5.

During this phase, the placements of the hawks are modified using the following equation:

$$\:X\left(t+1\right)=\left\{\begin{array}{c}Y\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\text{\:}\text{i}\text{f}\text{\:}F\left(Y\right)<F\left(X\right(t\left)\right)\\\:Z\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\text{\:}\text{i}\text{f}\text{\:}F\left(Z\right)<F\left(X\right(t\left)\right)\end{array}\right.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$
(21)

Hard besiege with progressive rapid dives: When the value of r is less than 0.5 and the absolute value of E is less than 0.5, the prey perceives that its energy is insufficient to flee. Therefore, the locations of hawks are updated by:

$$\:X\left(t+1\right)=\left\{\begin{array}{c}{Y}^{{\prime\:}}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\text{\:}\text{i}\text{f}\text{\:}F\left({Y}^{{\prime\:}}\right)<F\left(X\right(t\left)\right)\\\:{Z}^{{\prime\:}}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\text{\:}\text{i}\text{f}\text{\:}F\left({Z}^{{\prime\:}}\right)<F\left(X\right(t\left)\right)\end{array}\right.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$
(22)

where Y′ and Z′are determined by:

$$\:{Y}^{{\prime\:}}\hspace{0.25em}={X}_{\text{rabbit\:}}\left(t\right)-E\left|{X}_{\text{rabbit\:}}\left(t\right)-{X}_{m}\left(t\right)\right|\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$
(23)
$$\:{Z}^{{\prime\:}}={Y}^{{\prime\:}}+S\times\:LF\left(D\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$
(24)

Objective function for feature selection

Finally, the calculation of the fitness function (objective function) includes the error rate of the classifiers and a minimum number of selected features. The main goal of feature selection is to enhance the prediction accuracy of the proposed classification algorithms (SVM, RF, KNN, and XGBoost), which can be mathematically formulated as follows:

$$\:\downarrow\:Fitness\:Function\:=\:\alpha\:Error\:+\:\beta\:\frac{\left|F\right|}{\left|N\right|}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$
(25)

where Error is the error rate calculated by the classification algorithm, |F| is the number of selected features, |N| is the total number of features, and α \(\: \varepsilon\) [0; 1] and β = (1 − α) are two factors used to control the effect of the performance of the classification algorithm and feature size.

In a feature selection process using the binary Harris Hawks optimization (BHHO) algorithm, the solution is represented in binary form, where each bit can be either “0” or “1”. A bit value of “1” indicates that the corresponding feature is selected, while a bit value of “0” indicates that the feature is not selected, according to the transfer function55. For example, as shown in Table 1, out of a total of ten features, six were selected, demonstrating the algorithm’s capability to effectively identify the most relevant features.

Table 1 Example of a binary search space for BHHO.
Full size table

Classification algorithms

This section discusses the intelligence techniques used in the proposed model, to detect faults in PV system, namely the classification algorithms of Support Vector Machine algorithm, K-nearest neighbor algorithm, Random Forest algorithm, XGBoost algorithm.

K-nearest neighbor (KNN)

The K-Nearest Neighbors (KNN) algorithm is a popular classification technique known for its straightforwardness and effectiveness. The fundamental tenet of the K-nearest neighbors (KNN) algorithm is that features belonging to the same class exhibit proximity to one another inside the feature space. The classification decision is determined by the majority consensus among the K nearest neighbors of the object in issue56.

Nearest neighbors are determined using the Euclidean method, which is described as follows:

$$\:d\left(x,y\right)=\sqrt{\sum\:_{i=1}^{k}{({x}_{i},{y}_{i})}^{2}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$
(26)

where d(x, y) represents the Euclidean distance between points x and y in k-dimensional space. The coordinates of the points are given by x=(x1​,x2​,…,xk​) and y=(y1,y2,…,yk).

Support vector machine (SVM)

The Support Vector Machine (SVM) algorithm is based on the Vapnik-Chervoninskis (VC) theory. First introduced by Boser et al., they presented an algorithm that maximizes the difference between training data points57. The main objective of Support Vector Machines (SVM) is to determine the optimal hyperplane that can efficiently separate the data into two distinct classes, while maximizing the margin between them. The SVM algorithm is able to perform classification tasks, whether they are linear or nonlinear, depending on the characteristics of the data58, the optimal hyperplane is defined as the one that maximizes the difference between two classes of adjacent points, known as the support vector The decision function of the SVM is given as:

$$\:f\left(x\right)=sign\left(\sum\:_{i=1}^{N}{\alpha\:}_{i}{y}_{i}k\left({x}_{i},x\right)+b\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$
(27)

where:

x denotes the input vector to be segmented, \(\:{\alpha\:}_{i}\) the Lagrange coefficients, \(\:{y}_{i}\) the class labels of the training data,\(\:\:k\left({x}_{i},x\right)\) the kernel function, \(\:b\) the bias term.

The kernel function \(\:k\left({x}_{i},x\right)\) can map the input vectors into the SVM into a higher dimensional feature space and perform nonlinear classification where linear separation is possible.

By enhancing margins and reducing classification errors, SVM achieves better classification performance, making it a more robust and effective classifier.

Random Forest (RF)

The Random Forest (RF) method is a popular supervised machine learning technique mostly used for classification and regression applications. The method utilizes bagging ensemble learning, where many decision trees are built using different subsets of input data to improve prediction accuracy59. The cumulative prediction of all individual trees chosen by the majority given60, the final result of a random forest classification is established C(x) is denoted by the cumulative decision for a given sample x, calculated using the expected class score from each individual tree. The distribution equation is expressed as follows:

$$\:C\left(x\right)=\:mode\:\left[{Class}_{1},\:{Class}_{2},\:\dots\:,\:Clas{s}_{n}\:\right]\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$
(28)

where:

C(x) represents the final class label for the input sample x, Classi denotes the class label predicted by the i-th decision tree in the forest, n is the total number of decision trees in the forest.

EXtreme gradient boosting (XGBoost)

XGBoost (Extreme Gradient Boosting) is a high-performance boosting technique designed to minimize the loss function through various optimizations. It is a gradient boosting method that iteratively adds models to an ensemble, focusing on instances that the model struggles to predict correctly61. The core principle behind boosting is to enhance the model’s performance on difficult examples by directing subsequent weak learners to focus on these hard-to-predict instances. The XGBoost algorithm combines multiple simple prediction rules into a comprehensive and powerful predictor62. The complexity of the decision tree in XGBoost is quantified by the following equation:

$$\:B\left(ft\right)=\alpha\:A+\frac{1}{2}{\uplambda\:}\sum\:_{j=1}^{L}{\omega\:}_{j}^{2}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$
(29)

where:

\(\:B\left(ft\right)\) represents the complexity measure of the decision tree \(\:ft\), \(\:\alpha\:\:\)and λ are regularization parameters that control the complexity, \(\:A\) denotes the number of leaves in the decision tree, L is the total number of leaves, ωj the weight of the j-th leaf.

By minimizing this complexity measure along with the loss function, XGBoost effectively balances model accuracy and complexity, leading to a robust and efficient classification performance.

The iterative process of focusing on challenging examples and refining the model through successive boosting rounds results in a highly accurate and generalized classifier, making XGBoost a powerful tool for various machine learning tasks.

Evaluation measurements

The machine learning model analyzes new data and predicts the type of fault present in the PV system. The detection system can identify multiple fault conditions such as Healthy (the panel is functioning correctly), Dust (accumulation of dust on the panel surface), Shadow (partial shading on the panel affecting performance), Humidity (moisture affecting the panel), Open Circuit (disconnection in the electrical circuit), Short Circuit (a short in the circuit causing high current flow), and PV Degradation (long-term performance degradation of the PV panel). In machine learning, especially in classification tasks, it is important to evaluate the performance of the model. Several metrics are often used to evaluate the effectiveness of a model. Key assessment measures include accuracy, precision, recall, F1-score, and specificity. These metrics offer valuable information on several facets of the model’s performance, guaranteeing a comprehensive comprehension of its strengths and areas that need enhancement.

$$\:Accuracy=\frac{TN+TP}{TN+TP+FN+FP}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$
(30)

where:

TN: (True Negatives), TP: (True Positives), FN: (False Negatives), FP: (False Positives).

$$\:Precision=\frac{TP}{TP+FP}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$
(31)
$$\:Recall=\frac{TP}{TP+FN}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$
(32)
$$\:F1-score=\frac{2\left({Pr}ecision\times\:{Re}call\right)}{{Pr}ecision+{Re}call}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$
(33)
$$\:Specificity=\frac{TN}{TN+FP}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$
(34)

This evaluation measurement is important to understand how the classification model works. Accuracy provides general understanding, Precision focuses on optimal positive predictions, recall emphasizes the ability to identify all positive cases, F1-score balances Precision and Recall for detailed analysis, and specificity reflects the accuracy of the model in detecting anomalies.

Result and discussion

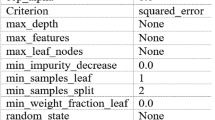
A Harris Hawks Optimization (HHO) algorithm combined with machine learning methods is proposed to address the feature selection challenge and enhance the reliability of photovoltaic (PV) systems. Table 2 outlines the key parameters of the HHO algorithm. Specifically, different feature subsets were selected by various machine learning classifiers from the dataset: K-Nearest Neighbors (KNN) selected subset F1 with 190 features, Support Vector Machine (SVM) selected subset F2 with 165 features, Random Forest (RF) selected subset F3 with 120 features, and XGBoost selected subset F4 with 130 features. Figure 10 illustrates the fitness values, showcasing the best results achieved by the HHO algorithm for each feature subset, demonstrating its effectiveness in optimizing feature selection.

Fig. 10
figure 10

Optimal Fitness Values Achieved by HHO for Feature Subsets Selected by Various Machine Learning Classifiers.

Full size image
Table 2 The HHO parameters.
Full size table

Figure 11 presents the convergence curve of the Harris Hawks Optimization (HHO) algorithm and the impact of parameter variations, illustrating the relationship between the number of iterations and the population size (number of hawks) in the context of feature selection. The curves represent hawk populations ranging from 5 to 25, increasing in increments of 5. As iterations progress, the fitness values generally decrease, showcasing the HHO algorithm’s capability to enhance the objective function over time. This decline in fitness values signifies convergence towards an optimal solution, a fundamental characteristic of optimization algorithms.

The curves highlight the impact of different population sizes on the optimization trajectory. Populations of 10 and 15 hawks demonstrate superior performance, achieving better fitness improvement rates and final values compared to smaller populations (5 hawks) or larger ones (20 and 25 hawks). This suggests that an optimal balance in population size is crucial for maximizing algorithm performance. The interplay between population size and iteration count is pivotal, underscoring the need for a well-balanced parameter selection to achieve effective optimization.

Additionally, among the 400 features in the original dataset, the XGBoost-HHO combination efficiently selected 130 features, labeled as F4, as depicted in Fig. 10. This reinforces the HHO algorithm’s effectiveness in identifying optimal feature subsets for reliable and enhanced PV system performance.

Fig. 11
figure 11

The impact of parameter variations for HHO.

Full size image

Table 3 provides a comparative analysis of the performance of the Harris Hawks optimization (HHO) algorithm for different feature subsets selected by different machine learning classifiers The evaluated metrics are best ftness, mean fitness, and standard deviation (STD).

The best fitness values ​​indicate the lowest error obtained when optimizing each feature subset, with F4 (XGBoost) having the lowest best fitness value of 0.0303, indicating high performance in selecting the most appropriate features compared to F3 (RF) 0.0395, followed F2 (SVM) was 0.0455, and F1 (KNN) was 0.0516.

Mean fitness values ​​give the average performance measure between iterations. F4 also outperforms the other methods with an average of 0.0416, much lower than the others. F1, F2, and F3 have the same fitness values ​​of about 0.0735, 0.0717, and 0.0720, respectively, indicating consistent performance in these methods but higher error rates compared to F4.

The standard deviation (STD) refers to the change in fitness values ​​across iterations. F4 exhibits the least variability with an STD of 0.0020, indicating a robust and reliable performance. In contrast, F1, F2, and F3 show high variability with STDs of 0.0089, 0.0121, and 0.0109, respectively.

Table 3 HHO performance across different feature subsets.
Full size table

The feature subset selected by XGBoost (F4) exhibits good performance in terms of best fitness, mean fitness, and STD, so it is the preferred choice for feature selection in this case. Low error rate and variability indicate F4 is more effective in determining the relative features for optimizing the PV system reliability.

Performance evaluation results classification algorithms

The proposed model is evaluated using experimental data including 658 samples. These samples are divided 70% for training and 30% for testing to evaluate the performance of classification algorithms (SVM, KNN, RF, XGBoost) combined with the Harris Hawks Optimization (HHO) algorithm. The evaluation includes seven cases: Case 1 = Healthy, Case 2 = Dust, Case 3 = Shadow, Case 4 = Humidity, Case 5 = Open Circuit, Case 6 = Short Circuit, Case 7 = PV degradation. According to performance metrics Precision (PER%), Recall (REC%), F1-score (F1-S). %), and specificity (SPE%).

Tables 4, 5 and 6, and 7 provide a comprehensive analysis of the integration of the HHO algorithm with four different machine-learning classifiers in K-Nearest Neighbors (KNN), Support Vector Machine (SVM), Random Forest (RF), and XGBoost to specify PV system cases.

Figure 12A–D show that across all classifications, the HHO-XGBoost consistently scores near-perfect on all metrics, and shows exceptional performance in accurately detecting all cases including health, dust, shadow, humidity, open circuit, short circuit, and PV degradation are included HHO’s accuracy -XGBoost, recall, F1-score, and specificity values ​​are an impressive 100% in most cases, demonstrating its robustness and reliability.

HHO-SVM and HHO-RF also show strong performance, especially excellent in Open Circuit, Short Circuit, and PV Degradation cases with 100% in all metrics but with slight differences in precision and recall compared to the HHO-XGBoost.

HHO-KNN performs well but exhibits slightly lower precision and recall in specific cases such as healthy and dusty compared to other classifiers. Despite these minor setbacks, it still maintains high performance.

Table 4 Performance Metrics for KNN-HHO Across different PV system cases.
Full size table
Table 5 Performance Metrics for SVM-HHO Across different PV system cases.
Full size table
Table 6 Performance Metrics for RF-HHO Across different PV system cases.
Full size table
Table 7 Performance Metrics for XGBoost-HHO Across different PV system cases.
Full size table
Fig. 12
figure 12

Radar Charts Comparing Performance Metrics of HHO with Different Machine Learning Classifiers Across PV System Cases.

Full size image
Table 8 Overall Performance Metrics of HHO Integrated with various machine learning classifiers.
Full size table
Fig. 13
figure 13

Comparative Analysis of Overall Performance Metrics for HHO Integrated with Various Machine Learning Classifiers.

Full size image

Table 8; Fig. 13 present the comparative analysis of the overall performance metrics of the combined Harris Hawkes Optimization (HHO) algorithm with four different machine learning classifiers: K-Nearest Neighbors (KNN), Support Vector Machine (SVM), Random Forest (RF), and XGBoost. The metrics considered are overall accuracy (ACC%), overall precision (PER%), overall recall (REC%), overall F1-score (F1-S%), and overall specificity (SPE%).

The HHO-XGBoost combination demonstrates excellent performance across all metrics, achieving a perfect score of 100% in Overall PER, REC, F1-S, and SPE, and an Overall ACC of 99.49%. This indicates its exceptional capability in accurately identifying and classifying all cases related to the health and operational conditions of the photovoltaic (PV) system.

HHO-RF and HHO-SVM also exhibit strong overall performance with similar scores for overall PER 94.12%, REC 100%, F1-S 96.97%, and SPE 98.80%, and overall ACC show little difference, HHO-RF is 97.98%, and HHO-SVM is 97.47%. These results highlight its high accuracy and reliability, especially for recall and specificity.

HHO-KNN, while still performing admirably, shows marginally lower scores compared to the other classifiers. It achieves an Overall ACC of 96.97%, Overall PER of 96.84%, Overall REC of 96.92%, Overall F1-S of 96.78%, and Overall SPE of 99.50%. Despite these minor deviations, HHO-KNN maintains a high level of performance, indicating its effectiveness in feature selection and classification within the PV system context.

Generally, HHO-XGBoost is the preferred choice for feature selection due to its high accuracy, recall, F1-score, and specificity, followed closely by HHO-RF and HHO-SVM, and HHO-KNN also demonstrated performance which manifested itself appropriately. For classifier selection of features in PV systems, these results demonstrated the robustness of the HHO algorithm when combined with advanced machine learning classifiers.

Validation and comparison with previous methods in the field

In order to ensure the quality of the proposed method through verification and comparison with previous methods in the field of PV system diagnosis, a new experimental dataset consisting of 132 samples was proposed to evaluate the efficiency of the proposed HHO-XGBoost model and compare it with previous methods. Table 9 explains these new 132 experimental samples, which serve as a basis for evaluating the performance of the proposed model and comparative analysis with previously used methods.

Table 9 New experimental samples.
Full size table

Table 10; Fig. 14 provide a detailed comparison of the results achieved by the proposed HHO-XGBoost model against existing methods, including GADF-ANN, PCA-SVM, PNN, and a Fuzzy Logic system. The evaluation focuses on the accuracy of diagnosing specific fault cases (Case 1 through Case 7) as well as the overall diagnostic accuracy. Notably, the proposed HHO-XGBoost technique demonstrates superior performance across the board, achieving the highest overall diagnostic accuracy of 98.48%. This surpasses GADF-ANN (96.21%), PNN (95.45%), Fuzzy Logic system (93.94%), and PCA-SVM (93.18%).

The enhanced performance of HHO-XGBoost can be attributed to the HHO algorithm’s ability to effectively select features for photovoltaic (PV) systems. These results highlight the strength of combining the HHO algorithm with XGBoost, yielding significantly better classification accuracy in diagnosing various health and operational conditions in PV systems across all fault cases.

Table 10 Validation and comparison with previous methods.
Full size table
Fig. 14
figure 14

Comparison of proposed HHO-XGBoost method with previous methods.

Full size image

Conclusion

This paper introduces an enhanced state detection method for PV systems, which facilitates real-time monitoring and data extraction through automated current-voltage (I-V) curves. These curves are analyzed under both normal operating conditions and various fault conditions, including dust, shadow, humidity, open circuit, short circuit, and PV degradation.

The proposed test bench, utilizing a DC-DC converter for data extraction, demonstrates high accuracy in identifying and analyzing different PV faults, proving its reliability for diagnosis.

The Harris Hawks (HHO) optimization algorithm, which has been proven in previous studies and is a novel advanced metaheuristic algorithm, is used to process the data and identify critical features. For precise classification of PV panel conditions, the HHO algorithm is integrated with various advanced classification algorithms, including KNN, SVM, RF, and XGBoost. The results indicate that the HHO-XGBoost combination surpasses other algorithms in terms of accuracy, recall, F1-score, and specificity. The HHO-RF and HHO-SVM algorithms also exhibit strong performance, while HHO-KNN yields satisfactory results. In the validation and comparison with previous methods, the proposed HHO-XGBoost model outperforms all other approaches, including GADF-ANN, PCA-SVM, PNN, and the Fuzzy Logic system. This superior performance underscores the model’s effectiveness in accurately diagnosing the condition of photovoltaic (PV) systems, further validating its robustness and reliability in fault detection and classification.

These findings highlight the effectiveness of combining the proposed hardware setup with advanced machine learning algorithms and AI techniques. The integration of the DC-DC converter with sophisticated AI-driven methods significantly enhances the accuracy and robustness of fault detection and classification in PV systems, demonstrating a powerful approach for real-time monitoring and diagnostic analysis.