Introduction

The flexible job shop scheduling problem (FJSP), first explored by Brucker and Schlie1 and Brandimarte2, evolved from the classic job shop scheduling problem (JSP). This problem poses a complex combinatorial optimization challenge involving multiple equalities and inequalities constraints. Due to its wide range of engineering applications and inherent complexity, FJSP has consistently attracted significant research attention3,4.

The FJSP with parallel batch (p-batch) processing operation (FJSP_PBPO), explored in this study enables multiple jobs to be processed jointly on the same machine, thus posing a challenge to the traditional constraint of the FJSP, where each machine can handle only one job at a time. This problem is motivated by real-world scenarios observed in electronic product testing workshops. In electronic product testing, the workshop devises an overarching testing process plan for prototypes of the same product model. These prototypes are grouped into distinct categories, and each group undergoes sequential testing operations according to specified sub-routes within the plan. Figure 1 illustrates a performance testing process plan for a mobile phone, where 14 prototypes are divided into 7 groups. Each group of prototypes is treated as a single job. However, certain prototypes necessitate cross-group combination testing, leading to parallel batch processing operation (PBPO) on the same machine, as illustrated by (O14, O24) and (O33, O44) in Fig. 1 The introduction of PBPO to the FJSP further complicates the already NP-hard nature of the FJSP4,5, making it significantly challenging to find viable and optimal solutions, which urgently needs resolution in electronic product testing workshops.

Fig. 1
figure 1

Performance testing process plan of the mobile phone.

Full size image

Recently, swarm-based metaheuristic algorithms have gained significant attention for addressing FJSP due to their efficiency in producing high-quality solutions6,7,8,9,10. Integrating FJSP_PBPO characteristics with advanced swarm-based metaheuristic mechanisms shows promise for improving optimization in this area. The walrus optimization algorithm (WaOA) is a relatively recent metaheuristic inspired by the behavior of walruses. It is known for its strong exploration capabilities and a balanced approach between exploration and exploitation. This balance allows the algorithm to avoid local optima and effectively explore the solution space, making it particularly well-suited for tackling global optimization problems. However, the algorithm uses a continuous encoding scheme, making it unsuitable for directly solving the FJSP_PBPO addressed in this study. Additionally, the No Free Lunch theorem asserts that no single algorithm is universally effective for all optimization problems, indicating that strong performance on one problem does not guarantee similar results on others11. In industrial applications, the selection, design, and fine-tuning of metaheuristic algorithms must consider the unique demands and characteristics of specific problems to optimize performance effectively12. Therefore, this study aims to leverage the potential of WaOA and improve it to better address the FJSP_PBPO and enhance its solution quality. The specific innovative contributions are as follows:

  1. (1)

    An optimization model for FJSP_ PBPO is formulated using mixed-integer programming (MIP).

  2. (2)

    An enhanced WaOA (eWaOA) is proposed specifically for FJSP_PBPO.

  3. (3)

    New encoding, conversion, inverse conversion and decoding schemes tailored to FJSP_PBPO are developed.

  4. (4)

    A random optimal matching initialization (ROMI) strategy is designed to generate diverse and high-quality initial solutions.

  5. (5)

    Enhancements to feeding, migration, and fleeing strategies, coupled with the introduction of a novel gathering strategy, enhance the algorithm’s effectiveness in both global exploration and local exploitation.

The subsequent sections are structured as follows: “Related works” section reviews literature on FJSP with p-batch processing and swarm-based metaheuristic algorithms for FJSP. “Description and modeling of FJSP_PBPO” section presents the problem description and model of FJSP_PBPO. “Walrus optimization algorithm” section details the mathematical modeling of WaOA. “The proposed improved WaOA for FJSP_PBPO” section outlines the design of the eWaOA, encompassing encoding, conversion and inverse conversion technique, decoding, population initialization, enhancements of WaOA’s strategies, and newly designed gathering strategy. “Computational experiments and real-word case study” section presents the created benchmark instances, along with the conducted experiments, engineering case study, and results. “Conclusion and future research” section provides the conclusions and the future work.

Related works

FJSP and FJSP with p-batch processing

Since its inception in the beginning of the 90s1,2, the FJSP has evolved significantly over the past three decades. During this time, researchers have incorporated additional resource constraints, including transport resources13,14,15,16, molds17, and dual human–machine resources18,19. Furthermore, new time-related constraints, such as setup times 20 and uncertain processing times21,22, have been introduced. These advancements continuously broaden the applicability of FJSP, aligning the problem more closely with the optimization demands of real-world workshops4. In addition, the FJSP with p-batch processing has also been extensively studied4,5, with a primary focus on wafer fabrication environments.

According to the standard three-field α|β|γ notation in scheduling, introduced by Graham et al.23, the FJSP with p-batch processing can be represented as FJ|p-batch |γ, where γ denotes the objective to be optimized. The objectives in these studies mainly include minimizing makespan (Cmax), total weighted tardiness (TWT), total tardiness (TT), total completion time (TC), total weighted completion time (TWC), maximum lateness (Lmax), maximum tardiness (Tmax), and number of tardy jobs (NTJ).

Many studies have proposed heuristic methods based on disjunctive graph (DG), with the most widely explored being variations of the shifting bottleneck heuristic (SBH) initially introduced by Adams et al.24. Mason et al.25,26 presented a modified SBH to address the FJ| p-batch |TWT. Experimental results show that their modified SBH outperforms dispatching rules and surpasses an MIP heuristic in all but small instances. To reduce computational costs, Mönch and Drießel27,28 adopted a two-layer hierarchical decomposition approach, using a modified SBH27 and a SBH enhanced by a genetic algorithm (GA)28 for sub-problems optimization. Mönch and Zimmermann29 further applied the SBH to the same problem in a multi-product setting. Barua et al.30 developed a SBH to optimize Lmax, TT, TC of the problem within a stochastic and dynamic environment using discrete-event simulation, demonstrating superior performance compared to traditional dispatching methods. Upasani et al.31 streamlined the problem by focusing on bottleneck machines in the DG while representing non-bottlenecks as delays, effectively balancing solution quality and computational effort. Sourirajan and Uzsoy32 introduced a SBH that employs a rolling horizon approach to create manageable sub-problems. Upasani and Uzsoy33 further integrated this rolling horizon strategy with the reduction approach proposed by Upasani et al.31. Pfund et al.34 expanded the SBH to optimize TWT, Cmax, and TC, employing desirability functions to evaluate criteria at both the sub-problems and machine criticality levels. Yugma et al.35 proposed a constructive algorithm for a diffusion-area FJSP, incorporating iterative sampling and simulated annealing (SA), which demonstrated effectiveness on real-world instances. Knopp et al.36 introduced a new DG and a greedy randomized adaptive search procedure (GRASP) metaheuristic combined with SA, yielding excellent results on benchmark and industrial instances. Ham and Cakici37,38 developed an enhanced optimization model employing MIP and constraint programming (CP) for the FJ| p-batch |Cmax, which was solved using IBM ILOG CPLEX. The computational results demonstrate that the proposed MIP model significantly reduces computational time compared to the original model, while the CP model outperforms all MIP models. Wu et al.39 introduced an efficient algorithm based on dynamic programming and optimality properties for scheduling diffusion furnaces. The developed algorithm not only surpasses human decision-making but also enhances productivity compared to existing methods.

The FJ|p-batch |γ has also been investigated across various other industrial environments. Boyer et al.40 investigated this problem in seamless rolled ring production, where jobs are processed in batch furnaces, often in a first-in, first-out sequence, resulting in a PBPO structure. Zheng et al.41 examined the JSP with p-batch processing, inspired by practical military production challenges, and proposed an auction-based approach combined with an improved DG for solution optimization. Xue et al.42 developed a hybrid algorithm integrating variable neighborhood search (VNS) with a multi-population GA to address this problem, validated in a heavy industrial foundry and forging environment. Ji et al.43 constructed a novel multi-commodity flow model for the FJ|p-batch |Cmax, introducing an adaptive large neighborhood search (ALNS) algorithm with optimal repair and tabu-based components (ALNSIT) to effectively solve large-scale instances.

The above research provides valuable references for this study. However, existing optimization methods for FJSP with p-batch constraints are challenging to apply directly to the scheduling requirements of electronic product testing workshops. The main reasons are as follows: (1) Most of the research above, particularly studies on wafer fabrication scheduling, primarily focuses on batch processing machines (BPMs) scheduling and multi-level local optimization. In contrast, electronic product testing requires integrated scheduling of all jobs and machines throughout the workshop. (2) Except for the studies by Xue et al.42 and Ji et al.43, the process plans of all jobs are similar, and all jobs require processing through BPMs (e.g., acid bath wet sinks, heat treatment machines). In contrast, in this study, job process plans vary significantly, and only the jobs forming the PBPO need to undergo specified p-batch processing in the BPMs. (3) In existing studies, batch processing decisions are dynamically made based on each job’s ready time and the capacity of the BPMs. In contrast, p-batching in this study pertains to specific operations from different jobs that must be processed jointly according to a predefined testing process plan.

Swarm-based metaheuristic algorithms for FJSP

Swarm-based metaheuristic algorithms are inspired by the collective behaviors observed in natural phenomena among mammals, birds, insects, and other organisms. Prominent examples include particle swarm optimization (PSO) (PSO)44, ant colony optimization (ACO)45, and artificial bee colony (ABC)46, which are considered classical swarm-based metaheuristic algorithms. These algorithms have been extensively applied to the FJSP. For instance, Ding and Gu developed an enhanced PSO for addressing the FJSP47. Shi et al.48 proposed a two-stage multi-objective PSO to tackle a dual-resource constrained FJSP. Zhang and Wong49 addressed the FJSP in dynamic environments using a fully distributed multi-agent system integrated with ACO. Li et al.50 introduced a reinforcement learning (RL) variant of the ABC for the FJSP with lot streaming.

In the past decade, swarm-based metaheuristic algorithms have seen rapid development, with new algorithms continually emerging. Notable examples include grey wolf optimization (GWO)51, whale optimization algorithm (WOA)52, satin bowerbird optimizer (SBO)53, emperor penguin optimizer (EPO)54, squirrel search algorithm (SSA) 55, harris hawks optimization (HHO)56, red deer algorithm (RDA)57, tuna swarm optimization (TSO)58, remora optimization algorithm (ROA)59, African vultures optimization algorithm (AVOA)60, white shark optimizer (WSO) 61, WaOA62, and walrus optimizer (WO)12. Some of these algorithms provide novel approaches for addressing (F)JSP.

Luo et al.6 introduced an advanced multi-objective GWO (MOGWO) aiming at minimizing both makespan and total energy consumption for the multi-objective FJSP (MOFJSP). Lin et al.63 introduced a learning-based GWO tailored for stochastic FJSP in semiconductor manufacturing. It employs an optimal computing budget allocation strategy to enhance computational efficiency and adaptively adjust parameters using RL.

Liu et al.7 combined the WOA with Lévy flight and differential evolution (DE) strategies to tackle the JSP. The Lévy flight boosts global search and convergence during iterations, while DE enhances local search capabilities and maintains solution diversity to avoid local optima. Luan et al.64 proposed an improved WOA (IWOA) for the FJSP, focusing on minimizing makespan. The IWOA features a conversion method to translate whale positions into scheduling solutions and employs a chaotic reverse learning strategy for effective initialization. Additionally, it integrates a nonlinear convergence factor and adaptive weighting to balance exploration and exploitation, and incorporates a VNS for enhanced local exploitation.

Ye et al.8 addressed the FJSP with sequence-dependent setup times and resource constraints by introducing a self-learning HHA (SLHHO) aimed at minimizing makespan. The SLHHO employs a two-vector encoding for machine and operation sequences, introduces a novel decoding method to handle resource constraints, and uses RL to intelligently optimize key parameters. Lv et al.10 developed an enhanced HHO for both static and dynamic FJSP scenarios. This enhanced algorithm incorporates elitism, chaotic mechanisms, nonlinear energy updates, and Gaussian random walks to reduce premature convergence.

Fan et al.65 introduced the genetic chaos Lévy nonlinear TSO (GCLNTSO) for the FJSP with random machine breakdowns, focusing on minimizing a combined index of maximum completion time and stability. He et al.66 developed an improved AVOA for the dual-resource constrained FJSP (DRCFJSP). Enhancements to the AVOA include employing three types of rules for population initialization, establishing a memory bank to store optimal individuals across iterations for improved accuracy, and implementing a neighborhood search operation to further optimize makespan and total delay. Yang et al.9 developed a hybrid ROA with VNS aimed at optimizing FJSP makespan. The algorithm incorporates a machine load balancing-based hybrid initialization method to enhance initial population quality and a host switching mechanism to improve exploration capabilities.

The advancements in FJSP research and engineering applications are notable, but the existing studies did not address PBPO constraints, which limits their applicability to FJSP_PBPO. Thus, new research is required to integrate the unique aspects of FJSP_PBPO with the selected swarm-based metaheuristic algorithms.

Description and modeling of FJSP_PBPO

The FJSP_PBPO extends the classic NP-hard problem FJSP5. It involves processing N jobs on M machines, with each job following a specific process plan composed of sequentially ordered operations. Each operation can be executed on a set of alternative machines with defined processing times. Additionally, some machines can process multiple operations from different jobs simultaneously, subject to PBPO constraints. The primary objective of the FJSP_PBPO is to determine the optimal processing order of each “task” (encompassing both operations and PBPO) on each machine to minimize the makespan (Cmax), while also respecting precedence relationships among operations within the same job and among tasks on the same machine. Building on the complexities of FJSP, FJSP_PBPO further increases problem intricacy by incorporating PBPO constraints. Table 1 presents an example of an FJSP_PBPO scenario with four jobs and four machines, where the values under each machine indicate the processing time for each task. As with FJSP, FJSP_PBPO assumes that:

  1. (1)

    All jobs can start processing at time 0, and all the jobs have the same priority.

  2. (2)

    All machines are available at time 0.

  3. (3)

    Each machine can handle only one task at a time.

  4. (4)

    Each job is processed on only one machine at a time.

  5. (5)

    Once a task begins on a machine, it must be completed without interruption.

  6. (6)

    Each task can only start processing after its preceding tasks have been completed.

  7. (7)

    All operations that form the PBPO must start and finish simultaneously.

Table 1 Instance of FJSP_PBPO.
Full size table

The FJSP_PBPO is defined using specific notations. Below, we provide a concise overview of these notations and the corresponding problem formulations.

M: total number of machines;

N: total number of jobs;

m: machine index;

\(Tu\): the task set for all the jobs;

\(u\): task index,\(u \in Tu\);

\(JP[u]\): the immediate job predecessor task(s) of \(u,u \in Tu\);

\(P_{u}^{m}\): the processing time of task \(u,u \in Tu\) on machine m;

\(S_{u}^{{}}\): the processing time of task \(u,u \in Tu\);

\(C_{u}^{{}}\): the completion time of task \(u,u \in Tu\);

\(P_{o}^{m}\): the corresponding processing time of specific operation \(o,o \in u\) on machine m;

\(S_{o}^{{}}\): the start time of specific operation \(o,o \in u\);

\(C_{o}^{{}}\): the completion time of specific operation \(o,o \in u\);

\(C^{m}\): the completion time of the last task on machine m;

\(C_{\max }\): makespan;

\(Q\) : a sufficiently large integer;

\(X_{u}^{m}\): decision variable representing whether task u is processed on the machine m;

$$X_{u}^{m} = \left\{ {\begin{array}{*{20}c} 1 & {{\text{machine }}m{\text{ is assigned to task }}u} \\ 0 & {{\text{elsewise}}} \\ \end{array} } \right.;$$

\(Y_{uv}^{{}}\): decision variable representing the order of two different tasks processed on the same machine;

\(Y_{uv}^{{}} = \left\{ {\begin{array}{*{20}c} 1 & \begin{gathered} {\text{if the task }}u{\text{ is processed before }} \hfill \\ {\text{the task }}v{\text{ on the same machine}} \hfill \\ \end{gathered} \\ 0 & {{\text{elsewise}}} \\ \end{array} } \right..\)

Based on this, an optimization model is constructed using MIP, with the objective of minimizing the maximum completion time.

$$C_{max} = \min \{ \max \{ C^{m} \} \} ,1 \le m \le M.$$
(1)

Subject to:

$$C_{u} - S_{u} = P_{u}^{m} \times X_{u}^{m} {, }\forall u,m,$$
(2)
$$\sum\limits_{m = 1}^{M} {X_{u}^{m} = 1{,}\forall u},$$
(3)
$$C_{u} \le C_{max} {,}\forall u,m,$$
(4)
$$C_{u} \le S_{v}^{{}} + Q \times (1 - Y_{uv} ),\forall u,v,m,$$
(5)
$$S_{u}^{{}} \ge \max \{ C_{u^{\prime}}^{{}} \} ,\forall m,u^{\prime} \in JP[u],$$
(6)
$$(S_{u}^{{}} \ge 0{)} \cup {(}C_{u}^{{}} \ge 0) \, \forall u,m,$$
(7)
$$(S_{o}^{{}} = S_{o^{\prime}}^{{}} ) \cup (C_{o}^{{}} = C_{o^{\prime}}^{{}} ),\forall m,o \in u,o^{\prime} \in u.$$
(8)

Equation (1) represents the optimization objective function. Equation (2) indicates that tasks cannot be interrupted during processing. Equation (3) states that each task can only be processed on one machine. Equation (4) ensures that the completion time of any task does not exceed the maximum completion time \(C_{max}\). Equation (5) ensures the precedence order between tasks on the same machine. Equation (6) guarantees the precedence order between tasks of the same job. Equation (7) asserts that the start and completion time of any task is non-negative. Equation (8) specify that the various operation of task u must start and finish simultaneously.

Walrus optimization algorithm

In WaOA, each walrus serves as a candidate solution in the optimization problem. Therefore, the position of each walrus within the search space determines the candidate values for the problem variables. The optimization process begins with a population of randomly generated walruses X, representing by D-dimensional random vectors, as defined by Eq. (9).

$$\begin{gathered} \, X_{p} = lb + rand(ub - lb) \hfill \\ \, X_{p} = [\begin{array}{*{20}c} {X_{p,1} } & {...} & {X_{p,j} } & {...} & {X_{p,D} } \\ \end{array} ] \hfill \\ \, 1 \le p \le P,1 \le j \le D, \hfill \\ \end{gathered}$$
(9)

where, \(\, X_{p}\) is the pth initial walrus (candidate solution), lb and ub are the lower and upper boundaries of the problem, rand is a uniform random vector in the range 0 to 1, \(X_{p,j} ,1 \le j \le D\) is the value of the jth decision variable of the initial walrus \(\, X_{p}\), P is the number of walruses in the population, i.e., the population size, D is number of decision variables. Based on the suggested values for the decision variables, the objective function of the problem can be evaluated, and the resulting fitness function \(F(X_{p} ),1 \le p \le P\) can be obtained.

Walruses are agents that perform the optimization process. Their positions are iteratively updated using feeding, migration, fleeing strategies until a termination condition is met. Each iteration follows a structured approach divided into three phases. In Phase 1, the WaOA utilizes feeding strategy to explore globally. In this phase, the best candidate solution so far is identified as the strongest walrus \(X_{str}^{{}}\) according their fitness. Other walruses adjust their positions under the guidance of \(X_{str}^{{}}\) according to the Eqs. (10) and (11).

$$X_{p,j}^{t + 1} = X_{p,j}^{t} + rand_{p,j} \times (X_{str,j}^{{}} - I_{p,j} \times X_{p,j}^{t} ),1 \le p \le P,1 \le j \le D,$$
(10)
$$\, X_{p}^{t + 1} = \left\{ {\begin{array}{*{20}c} {X_{p}^{t + 1} ,} \\ {X_{p}^{t} ,} \\ \end{array} \begin{array}{*{20}c} {F(X_{p}^{t} ) < F(X_{p}^{t + 1} )} \\ {else,} \\ \end{array} } \right.$$
(11)

where \(X_{p,j}^{t + 1}\) is the new position for the pth walrus on the jth dimension, \(X_{p,j}^{t}\) is the current position for the pth walrus on the jth dimension, randp,j is a random number lies in the range (0,1), \(X_{str,j}^{{}}\) is the position for the strongest walrus \(X_{str}^{{}}\) on the jth dimension, \(I_{p,j}\) is an integer selected randomly between 1 or 2.

In Phase 2, each walrus migrates to a randomly selected walrus position in another area of the search space and the new position for each walrus can be generated according to Eqs. (12) and (13).

$$X_{p,j}^{t + 1} = \left\{ {\begin{array}{*{20}c} {X_{p,j}^{t} + rand_{p,j} \times (X_{k,j}^{t} - I_{i,j} \times X_{p,j}^{t} ),} & {1 \le p,k \le P,1 \le j \le D,\;if \, F(X_{k}^{t} ) \ge F(X_{p}^{t} )} \\ {X_{p,j}^{t} + rand_{p,j} \times (X_{p,j}^{t} - X_{k,j}^{t} ),} & {1 \le p,k \le P,1 \le j \le D,\;if \, F(X_{k}^{t} ) < F(X_{p}^{t} )} \\ \end{array} } \right.,$$
(12)
$$\, X_{p}^{t + 1} = \left\{ {\begin{array}{*{20}c} {X_{p}^{t + 1} ,} \\ {X_{p}^{t} ,} \\ \end{array} \begin{array}{*{20}c} {F(X_{p}^{t} ) < F(X_{p}^{t + 1} )} \\ {else,} \\ \end{array} } \right.$$
(13)

where \(X_{k}^{t} ,1 \le k \le P\) and \(k \ne p\) is the position of the selected walrus to migrate the pth walrus towards it, \(X_{k,j}^{t} ,1 \le k \le P,1 \le j \le D\) is its jth dimension, and \(F(X_{k}^{t} )\) is its objective function value.

In Phase 3, the WaOA utilizes fleeing strategy to adjust the positions of each walrus within its neighborhood radius. This strategy is used to exploit the problem-solving space around candidate solutions. The new position can generate randomly in this neighborhood using Eqs. (14) and (15).

$$\begin{gathered} X_{p,j}^{t + 1} = X_{p,j}^{t} + \left( {lb_{local,j}^{t} + \left( {ub_{local,j}^{t} - rand \cdot lb_{local,j}^{t} } \right)} \right) \hfill \\ \, local\;bound:\left\{ {_{{ub_{local,j}^{t} = ub_{j} /t}}^{{lb_{local,j}^{t} = lb_{j} /t}} } \right., \hfill \\ \end{gathered}$$
(14)
$$\, X_{p}^{t + 1} = \left\{ {\begin{array}{*{20}c} {X_{p}^{t + 1} ,} \\ {X_{p}^{t} ,} \\ \end{array} \begin{array}{*{20}c} {F(X_{p}^{t} ) < F(X_{p}^{t + 1} )} \\ {else,} \\ \end{array} } \right.$$
(15)

where \(lb_{j}\) and \(ub_{j}\) are the lower and upper bounds of the jth position, respectively, \(lb_{local,j}^{t}\) and \(ub_{local,j}^{t}\) are allowable local lower and upper bounds for the jth position, respectively. The pseudocode for WaOA is shown in Algorithm 1.

Algorithm 1
figure a

Walrus optimization algorithm (WaOA).

Full size image

The proposed improved WaOA for FJSP_PBPO

Framework of the eWaOA

Due to the introduction of new constraints by FJSP_PBPO, existing encoding, conversion, and decoding methods for swarm-based metaheuristics used in FJSP are not directly applicable. Consequently, we first develop new encoding, conversion, inverse conversion and decoding schemes tailored to these constraints. Preliminary experiments have identified several shortcomings of the original WaOA when applied to FJSP_PBPO, such as premature convergence to local optima and inefficient updates. To address these issues, this study first create new initialization strategy and then enhance the WaOA’s feeding, migrating, and fleeing strategies. Additionally, a gathering strategy is introduced to enhance both global and local optimization capabilities. The framework for the proposed eWaOA is illustrated in Fig. 2 and detailed below.

Fig. 2
figure 2

Flowchart of the proposed eWaOA for the FJSP_PBPO.

Full size image

Step 1—Data input: Operation set, operation sequence for the N jobs, alternative machines with their associated processing times for each operation, and the PBPOs, with both operations and PBPOs collectively described as tasks.

Step 2—Parameter setting: Population size (P) of walruses, termination parameter (maximum iterations maxT or time limit T), control factor A, and matching parameter K for ROMI.

Step 3—Population initialization: The optimization process begins with P randomly generated walruses based on the ROMI strategy according to the parameter K. Each walrus is encoded as a real vector \(X_{p} ,1 \le p \le P\) and an integer vector \(X_{p}^{\prime} ,1 \le p \le P\). On this basis, segmented conversion are developed to convert the \(X_{p}\) to \(X_{p}^{\prime}\), while the inverse conversion method is created to transform the \(X_{p}^{\prime}\) into \(X_{p}\). The \(X_{p}^{\prime}\) are decoded using a designed semi-active decoding method to generate feasible scheduling scheme.

Step 4—Update the position of each walrus. Walruses serve as search agents in the optimization process, with their positions continuously updated through enhanced feeding, migration, fleeing strategies, or through the enhanced feeding and introduced gathering strategy. The decision between choosing the gathering strategy or the migration and fleeing strategies is controlled by A. For the feeding, migration, and fleeing strategies, real vectors X are updated directly during each iteration, with simultaneous conversion of the updated real vector \(X_{new}\) into corresponding integer vector \(X_{new}^{\prime}\). Conversely, gathering strategy involve direct updates of \(X_{{}}^{\prime}\) to generate \(X_{new}^{\prime}\), followed by inversely converting it to corresponding \(X_{new}\). This ensures synchronization in updating the X and \(X_{{}}^{\prime}\) at each iteration.

Step 5—Updating the strongest walrus: Each \(X_{new}^{\prime}\) are decoded into a feasible semi-active schedule for FJSP_PBPO, and the fitness values of the walruses is assigned the reciprocal of makespan corresponding to the schedule. And the walrus with the highest fitness so far is update as the strongest walrus \(X_{str}^{{}}\).

Step 6—Termination criterion: If the iterations reaches its preset maxT or the runtime reaches its preset T, the best solution is output, and the iteration stops; else, it proceeds to Step 4.

Representation of walrus and FJSP_PBPO

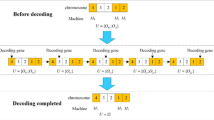
In our eWaOA, a vector \(X_{p} = \{ X_{p,1} ,X_{p,2} ,...X_{p,D} \}\) is represented as a D-dimensional real vector, constrained by the specific requirements of the problem. FJSP_PBPO involves two sub-problems: task sequencing and machine assignment. Therefore, Xp should encompass information from both aspects. Let TN denote total number of all tasks in the FJSP_PBPO, then D = 2TN. The first half part \(X1_{p} = \{ X_{p,1} ,X_{p,2} ,...X_{p,TN} \}\) of \(X_{p}\) represent task sequencing, while the second half part \(X2_{p} = \{ X_{p,TN + 1} ,X_{p,TN + 2} ,...X_{p,2TN} \}\) describes machine assignment for each task. Specifically, \(X_{p,j} ,1 \le j \le TN\) denotes the value of the jth task decision variable in the vector \(X_{p}\), \(X_{p,j} ,TN < j \le 2TN\) represents the machine assignment decision variable for the (j-TN)th task of \(X_{p}\). The \(X1_{p}\) is defined as the real sub-vector for task (RVT) and \(X2_{p}\) is defined as the real sub-vector for machine assignment (RVM) in this study. Additionally, the value of \(X_{p,j} ,1 \le j \le 2TN\) is bound to be in the real range (-N, N), where N is the total number of jobs.

The WaOA is designed for continuous functions but is not directly applicable to discrete problems such as FJSP_PBPO. Additionally, the presence of PBPO implies that a single position in \(X1_{p}\) may correspond to multiple operations across different jobs. Consequently, decoding \(X_{p}\) into a feasible schedule and evaluating the objective function value presents significant challenges. To address these issues, we further propose a task-based encoding method for FJSP_PBPO. This encoding scheme consists of an integer vector divided into two parts. The first part, the integer sub-vector for tasks (IVT), represents each position with job ID(s). To maintain consistency, the number of elements in each position is set to \(s = \max \{ |PBPO_{k}^{{}} |\} ,\forall k\), and the length of the vector is set to the number of tasks (TN), where \(|PBPO_{k}^{{}} |\) is the number of operations in the k-th PBPO. Positions with fewer than s elements are padded with zeros. If a position contains more than one job ID, it indicates that the position corresponds to a PBPO. For simplicity, padded zeros are omitted in the subsequent description. The second part, the integer sub-vector for machine assignment (IVM), has positions with potential values ranging from 1 to M. Each position in IVM corresponds to the processing machine for the task indicated by the same position in IVT. Figure 3 illustrates the integer vector code for FJSP_PBPO, showing the specific operations or PBPOs in IVT and their corresponding processing times. Thus, each walrus contains both continuous encoding vector \(X_{p} = [RVT,RVM]\) and integer vector \(X_{p}^{\prime} = [IVT,IVM]\).

Fig. 3
figure 3

An instance of two integer sub-vectors code for the FJSP_PBPO.

Full size image

Conversion and inverse conversion scheme

The conversion process transforms a real vector to integer vector, allowing the eWaOA to solve FJSP_PBPO. The ranked order value (ROV) rule, originally designed for FJSP or JSP, uses order relationships and random keys to map a real vector into an integer operation sequence, which outlines the order of operations on all machines and forms a scheduling scheme7,65. However, the inclusion of PBPO in the FJSP_PBPO renders the traditional ROV method unsuitable. To address this, a novel segmented conversion algorithm is developed to convert the real vector \(X_{p} = [RVT \, RVM]\) into integer vector \(X_{p}^{\prime} = [IVT,IVM]\). This algorithm introduces a task template (TP) segmented into three sections: the first section corresponds to tasks from jobs without PBPO; the second section consists of sequential PBPO tasks; and the third section includes tasks from jobs with PBPO, excluding the PBPOs themselves. For each segment, elements in the RVT are categorized and converted based on the methods outlined in Table 2 ensure that the constraints are maintained. Additionally, when converting the RVM to the IVM, the machine index for each task must be determined first, with the conversion formula provided in Eq. (16):

$$MI_{j} = \left\lfloor {\frac{{(RVM_{j} + N) \times s(j)}}{2N}} \right\rfloor + 1,TN + 1 \le j \le 2TN,$$
(16)

where N denotes the number of jobs, TN represents total number of all tasks,\(s(j)\) indicates the total number of alternative machines for the task \(IVT_{j - TN} ,TN + 1 \le j \le 2TN\). The segmented conversion algorithm is described as follows:

Algorithm 2
figure b

Segmented conversion.

Full size image
Table 2 Categorization and post-processing strategy of a RVT.
Full size table

Figure 4 illustrates an example of the segmented conversion process from RVT to IVT. First, the task template TP is created with three sections according to the job process plan: the first section, from \(TP_{1}\) to \(TP_{4}\), contains tasks for jobs without PBPO; the second section consists of sequentially arranged PBPO tasks \(TP_{5}\) and \(TP_{6}\); and the third section, from \(TP_{7}\) to \(TP_{14}\), includes tasks for jobs with PBPO but excludes the PBPOs themselves. The RVT is divided into three sections according to the TP structure, and its elements of RVT is copy to CRVT. Next, related values in the second and third sections of the CRVT are updated according to the conversion formulas given in Table 2. In this example, since O22 in {O22, O33} is a predecessor of O24 in {O24, O43}, the value 3.28 in RVT for {O22, O33} is initially converted to -0.03 in CRVT using the “Predecessor” conversion formula. Subsequently, the “Predecessor”, “Middle”, and “Successor” conversion formulas are applied sequentially to convert the predecessor tasks for {O22, O33} and {O24, O43}, as well as the tasks O23 (middle of the two PBPOs) and the successor tasks. The original RVT values and their converted counterparts in the CRVT for the example in Table 2, are highlighted in red in Fig. 4 Finally, the ranked values of each element in the CRVT are obtained to generate the ROV vector. Following the ascending order of the ROV vector, job IDs are sequentially copied from corresponding positions in the TP to construct the IVT.

Fig. 4
figure 4

Example of the segmented conversion from RVT to IVT.

Full size image

The inverse conversion is designed to transform \(X_{p}^{\prime}\) to \(X_{p}\) while ensuring that the updates of \(X_{p}^{\prime}\) remains consistent with the update of \(X_{p}\). When converting the IVT to the RVT, a randomly generated RVT is introduced, and the ROV is determined based on the TP and IVT. Then, the RVT is reordered according to the ROV, and the corresponding values in RVT are updated based on the categorization strategies in Table 3, forming the new RVT. When converting IVM to RVM, the value corresponding to each task are first obtained using the following Eq. (17).

$$RVM_{j} = [\frac{{2 \times N \times (MI_{j} - 1) - N \times s(j)}}{s(j)}] + \frac{N}{s(j)},TN + 1 \le j \le 2TN,$$
(17)

where \(MI_{j}\) is the machine index of the \(j - TN\) th task, the mean of N, TN and \(s(j)\) consistent with those in Eq. (16). This inverse conversion process is detailed in Algorithm 3.

Algorithm 3
figure i

Inverse conversion.

Full size image
Table 3 Categorization and post-processing strategy of a RVT for inverse conversion.
Full size table

Figure 5 illustrates an example of the inverse conversion from IVT to the RVT. First, the positions of each TP element within the IVT are recorded to construct the ROV vector. For instance, the 12th and 7th elements of TP, with values (4, 1) and (2, 1) respectively, rank first and second in the IVT. Consequently, the 12th and 7th positions in the ROV vector are assigned the values 1 and 2, respectively. Next, a Reordered RVT is generated by sorting the RVT according to the ROV vector. For example, as shown in the figure, the first and second elements of the ROV vector are 3 and 5, respectively, so the third and fifth elements of the RVT are placed into the first and second positions of the Reordered RVT. Subsequently, the values in the Reordered RVT are converted according to the strategies outlined in Table 3 to generate NewRVT. The conversion process first applies to non-PBPO predecessor tasks, O23 (between the two PBPOs {O22, O33}, {O24, O43}), as well as the successor tasks for both PBPOs. Then, the conversion is performed for {O22, O33}, the predecessor tasks for {O24, O43}. The red-highlighted text in the Reordered RVT and NewRVT in Fig. 5 indicates the corresponding values before and after the inversion conversion, as shown in Table 3.

Fig. 5
figure 5

Example of the inverse conversion from IVT to RVT.

Full size image

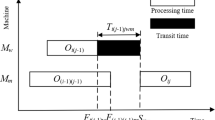
Semi-active decoding

Bierwirth and Mattfeld67 introduced decoding methods that transform encoded permutations into semi-active, active, non-delay, and hybrid schedules. Among these, the semi-active schedule is particularly straightforward to implement, provides high decoding efficiency, and frequently produces high-quality solutions. Therefore, the semi-active decoding is adopt to decode the \(X_{p}^{\prime} = [IVT \, IVM]\) for a walrus. This decoding approach ensures that each task adheres to the precedence constraints both within the same job and on the same machine. However, for the FJSP_PBPO, it is crucial to thoroughly evaluate the completion times of all predecessors for each job in the PBPO. The constraints considered during the decoding process become more complex. The specific semi-active decoding designed for FJSP_PBPO is outlined in Algorithm 4.

Algorithm 4
figure p

Semi-active decoding.

Full size image

Random optimal matching-based initialization

To quickly obtain high-quality initial solutions, it is necessary to comprehensively balance the quality and diversity of the initial population during the initialization. For the optimization of FJSP_PBPO, the quality of the corresponding initial population is related to the matching of task and machine assignment. Based on this, a ROMI method is proposed to initialize the population. Specifically, for each walrus \(X_{p} ,1 \le p \le P/2\) in the first half of the population, one RVT and K RVM are generated randomly accordingly to \(RVT = - N + rand(2N)\), \(RVM_{k} = - N + rand(2N),1 \le k \le K\), respectively, where N is the number of jobs. Then, segmented conversion and semi-active decoding are employed to determine the makespan of the matched \(RVT\) and \(RVM_{k} ,1 \le k \le K\), and the pair of RVT and \(RVM_{k^{\prime}}\) with the smallest makespan is selected to initialize \(X_{p} = [RVT,RVM_{{^{k^{\prime}} }} ],1 \le p \le P/2\).

Conversely, for each walrus in the second half of the population \(X_{p} ,P/2 + 1 \le p \le P\), K RVT and one RVM are generated randomly accordingly to \(RVT_{k} = - N + rand(2N),1 \le k \le K\), \(RVM = - N + rand(2N)\), respectively. Similarly, the pair of \(RVT_{k^{\prime}}\) and RVM with the smallest makespan is selected to construct \(X_{p} = [RVT_{k^{\prime}} ,RVM]\). Since the RVT in the first half and the RVM in the second half of the population are generated randomly, the randomness and diversity of the initial population generation are ensured.

Enhanced feeding strategy

In the original feeding strategy of WaOA, each walrus moves toward the strongest individual \(X_{str}\) in the population. And a random number randp,j within the interval (0,1) controls how each dimension of a walrus approaches the \(X_{str}\), limiting the solution space. Preliminary experiments indicate that when solving the FJSP_PBPO, walruses often get stuck in local optima and experience a slower convergence speed. To enhance the global search capability and efficiency of WaOA, Lévy flight68 is incorporated into the feeding strategy. Many animals, including walruses, perform fine-grained searches within a localized area for a period, followed by longer movements to explore other regions. Lévy flight, which alternates between short-distance searches and occasional long-range moves, effectively models this behavior and aligns well with the natural feeding patterns of walruses. The feeding strategy, now integrated with Lévy flight for updating walrus positions, can be expressed by modifying the previous formula as follows:

$$X_{p,j}^{t + 1} = X_{p,j}^{t} + sign[rand_{p,j} - 0.5] \times (X_{str,j}^{{}} - I_{p,j} \times X_{p,j}^{t} ) \oplus Levy(s),\quad 1 \le p \le P,1 \le j \le D,$$
(18)

where sign [rand − 0.5] can take one of three values: − 1, 0, or 1. ⊕ means entry wise multiplication.

Lévy flight is a kind of non-Gaussian random process, and its step length obeys a Lévy distribution.

$$Levy(s)\sim \left| s \right|^{ - 1 - \beta } ,\quad 0 < \beta \le 2,$$
(19)

where s represents the step length of the Lévy flight, and β is an index parameter. The value of s can be calculated using Mantegna’s algorithm as follows:

$$s\sim \frac{u}{{|v|^{1/\beta } }},$$
(20)

where β is set to be 1.5, and both μ and v follow normal distributions.

$$\sigma = [\frac{\Gamma (1 + \beta ) \times sin(\pi \beta /2)}{{\Gamma ((1 + \beta )/2) \times \beta \times 2^{(\beta - 1)/2} }}]^{1/\beta } ,$$
(21)

where Γ denotes the standard Gamma function. According to Eqs. (18)–(21), Eq. (18) can be reformulated as:

$$X_{p,j}^{t + 1} = X_{p,j}^{t} + sign[rand_{p,j} - 0.5] \times \frac{u}{{|v|^{1/\beta } }} \times (X_{str,j}^{{}} - I_{p,j} \times X_{p,j}^{t} ),\quad 1 \le p \le P,1 \le j \le D.$$
(22)

Enhanced migration strategy

In the original migration strategy of the WaOA, each walrus randomly selects another walrus from the population as its migration destination. Throughout the iteration process, the updates of the walruses lack an adaptive adjustment mechanism, leading to slower convergence speeds or entrapment in local optima. To enhance global exploration in the early stages and strengthen local exploitation in the later stages of iteration, the migration strategy of WaOA is modified by introducing a self-adjusting factor C to replace rand in Eq. (12). The position update formula for walrus can then be rewritten as:

$$X_{p,j}^{t + 1} = \left\{ {\begin{array}{*{20}c} {X_{p,j}^{t} + C \times (X_{k,j}^{t} - I_{i,j} \times X_{p,j}^{t} ),1 \le p \le P,1 \le j \le 2TN,\;if \, F(X_{k,j}^{t} ) \ge F(X_{p,j}^{t} )} \\ {X_{p,j}^{t} + C \times (X_{p,j}^{t} - X_{k,j}^{t} ),1 \le p \le P,1 \le j \le 2TN,\;if \, F(X_{k,j}^{t} ) < F(X_{p,j}^{t} )} \\ \end{array} } \right.,$$
(23)
$$C = \left[ {\frac{1}{2} + \cos \left( {\frac{\pi }{2} \times \frac{t}{T}} \right)} \right] \times rand,$$
(24)

where t denotes the current iteration number and T represents the maximum number of iterations. In the early stages, when t is relatively small, the value of C is large, allowing individuals to explore with a greater step size during position updates. This facilitates rapid coverage of a broader search space and enhances global exploration. As the iterations progress, t gradually increases while C decreases. In the later stages, a smaller value of C promotes fine local exploitation within these improved regions, enhancing the algorithm’s convergence efficiency.

Enhanced fleeing strategy

The original update expression for the fleeing strategy is shown in Eqs. (14) and (15). However, the local lower bound and upper bound in the Eq. (14) is controlled by the inverse proportional function \(lb_{local,j}^{t} = lb_{j} /t\) and \(ub_{local,j}^{t} = ub_{j} /t\) respectively. The inverse proportional function prioritizes global exploration at the beginning of the algorithm’s iterations, with a larger radius to discover optimal regions within the search space. However, the neighborhood radius of the inverse proportional function decays rapidly, leading to a quick decline in global exploration capability, which makes it difficult for the fleeing strategy to play an exploitation role in the later stages of the algorithm. Therefore, this study replaces the original inverse proportional function with an arctangent function to control the local bound in fleeing. Then the fleeing strategy can be mathematically modelled by the Eq. (25).

$$\begin{gathered} X_{p,j}^{t + 1} = X_{p,j}^{t} + \left( {lb_{local,j}^{t} + \left( {ub_{local,j}^{t} - rand \cdot lb_{local,j}^{t} } \right)} \right) \hfill \\ new\;local\;bound:\left\{ {_{{ub_{local,j}^{t} = ub_{j} \times \frac{{\frac{\pi }{2} - \arctan (\frac{t - 0.5 \cdot T}{{0.03 \cdot T}})}}{\pi }}}^{{lb_{local,j}^{t} = lb_{j} \times \frac{{\frac{\pi }{2} - \arctan (\frac{t - 0.5 \cdot T}{{0.03 \cdot T}})}}{\pi }}} } \right., \hfill \\ \end{gathered}$$
(25)

where the mean of t and T consistent with those in Eq. (24).

Gathering strategy

Walruses enhance their foraging and movement efficiency by interacting and sharing ___location information with one another. To model this behavior, we propose a “gathering strategy” in which walruses form pairs and exchange information, thereby improving the herd’s ability to identify areas with higher food availability. To assess this information-sharing process, walruses are paired through a random selection method. Based on these paired walruses, such as Xp't and \(X^{\prime t}_{p^{\prime}}\), the position of each individual is updated according to the following Algorithm 5.

Algorithm 5
figure q

Gathering strategy.

Full size image

A control factor, denoted as A, is introduced to regulate the population’s updating strategy. If A reaches or exceeds 0.4 after the feeding strategy, walruses will adopt migration, fleeing strategies to explore and exploit search area. Conversely, if A falls below 0.4, a gathering strategy will be employed. In this strategy, walruses search for new territories in pairs. Multiple pairs will form within the walrus population, thereby further enhancing search range. The value of A is controlled by the Eq. (26):

$$A = \frac{{e - e^{{[(t - 1)/T]^{2} }} }}{e - 1} \cdot \left| {\sin (2\pi \times rand)} \right|,$$
(26)

where the rand denotes a random number between 0 and 1.

Enhanced WaOA for FJSP_PBPO

Based on the above improvements, the pseudocode of the proposed eWaOA for FJSP_PBPO in this study is outlined in Algorithm 6. The eWaOA is initialized using the ROMI strategy, and the mathematical models for the enhanced feeding, migration, fleeing strategies are shown in Eqs. (18)–(25), in combination with Eqs. (11), (13), and (15). The gathering strategy is described in Algorithm 5.

Algorithm 6
figure r

eWaOA for FJSP_PBPO.

Full size image

Computational complexity analysis

In the proposed eWaOA, the key components contributing to computational complexity include conversion and inverse conversion, population initialization, decoding, an enhanced feeding strategy, an enhanced migration strategy, an enhanced fleeing strategy, and a gathering strategy. Notably, population initialization, decoding, as well as the enhanced feeding, migration, fleeing, and gathering strategies, all involve either conversion or inverse conversion operations. Let P denote the population size, D represent the dimension of each individual, TN denote the total number of all tasks in the FJSP_PBPO (where D = 2TN), K be the parameter in the ROMI strategy, and T be the maximum number of iterations.

Conversion involves task template partitioning, data duplication, updating CRVT-related values, constructing the IVT, and determining machine indices, each with a time complexity of O(D). The corresponding inverse conversion process includes obtaining the ROV vector, generating random vectors, updating NewRVT values, and computing the RVM, all with a time complexity of O(D). Therefore, the time complexity of both conversion and inverse conversion is O(D). For decoding, the primary time consumption is spent iterating through the task sequence. For each task, it is necessary to retrieve the task, machine, and processing time, as well as determine the task’s start and completion time. Since the loop runs for a total of TN tasks, the time complexity is O(TN).

The computational complexity of population initialization using the ROMI strategy is O(PKD). For each individual in the first half of the population (a total of P/2 individuals), 1 task sequence random vectors (RVTs) and K machine assignment random vectors (RVMs) are generated. For each individual in the second half of the population (a total of P/2 individuals), K RVTs and 1 RVM are generated. The time complexity of generating each random vector is O(TN). Since the initialization process for each individual involves both conversion and decoding operations, their respective time complexities are O(D) and O(TN). Therefore, the total time complexity of generating random vectors is O(P/2(1 + K) × (TN + TN + D) + P/2(1 + K) × (TN + TN + D) = O(PKD).

The enhanced feeding, migration, fleeing, and gathering strategies each have a computational complexity of O(PD) per iteration. This complexity arises because, for each dimension of every walrus, calculating the new position involves operations such as multiplication, addition, and random number generation, all with a constant time complexity of O(1). Furthermore, the conversion or inverse conversion process for each walrus has a complexity of O(D). Given a population size of P, updating the positions of all walruses leads to a total time complexity of O(PD). Hence, the overall complexity of these strategies is O(PD).

Therefore, the overall computational complexity of the eWaOA is expressed as O(PDK + TPD). Since the value of K is generally much smaller than the maximum number of iterations T, the total computational complexity can be simplified to O(TPD).

Computational experiments and real-word case study

We first develop 30 test instances based on existing benchmark FJSP instances. We then compare the performance of original WaOA with WaOA that incorporates the ROMI initialization strategy (WaOA-R) to assess the effectiveness of the ROMI approach. Subsequently, we design and conduct experiments with four enhanced WaOA variants and eleven state-of-the-art (SOTA) metaheuristic algorithms across these test instances, followed by a real-world engineering case study to evaluate the superiority of eWaOA. To ensure the stability and reliability of the results and minimize the effects of randomness, we run each test instances and engineering case ten times. The experiments are performed using MATLAB R2018a on a desktop computer equipped with an Intel Core i7-8700 processor, 16 GB of RAM, and Windows 10.

Instance generation

Due to the absence of benchmark for FJSP_PBPO, this study extends the MK01–MK15 benchmarks provided by Brandimarte2 by introducing one or two randomly selected PBPOs to create new test instances, resulting in the EMK01-EMK15 benchmarks for FJSP_PBPO. Detailed information about these PBPOs is presented in Table 4.

Table 4 Description of the test instances.
Full size table

All other data remain consistent with the original benchmarks. For example, in EMK02, the first PBPO consists of tasks O34 and O93, which can be processed on machines 2, 5, and 6 with processing times of 4, 2, and 3 units, respectively. The second PBPO includes tasks O82 and O10(3), which are processed on machines 4 and 6 with processing times of 5 and 3 units, respectively. Test instances are identified with the suffixes “s” and “d”, where “s” denotes instances considering only the first PBPO, and “d” denotes instances that include both PBPOs. Accordingly, the test instances are EMK01(s)-EMK15(s) and EMK01(d)-EMK15(d), totaling 30 instances. The extension to additional PBPOs follows the same principle as the scenario with two PBPOs, as these two PBPOs are generated randomly.

Parameter setting and notations

The performance of an algorithm is significantly influenced by its parameter configurations, which are selected based on extensive experimental validation and practical experience to ensure optimal results within a reasonable time. In this study, the parameters are configured as follows: the walrus population size is set to 200, maximum iterations is 250, different T are assigned based on the scale of each case when using time limit as the termination criterion, the parameter K in the ROMI is set to 7, as determined by the experiments discussed in “Effectiveness of ROMI” section.

To facilitate subsequent discussions and analyses, this paper standardizes the naming and descriptions for the algorithm variants as follows: WaOA-R denotes the original WaOA enhanced with ROMI strategy; WaOA-RF builds upon WaOA-R by incorporating the enhanced feeding strategy; WaOA-RFM further advances WaOA-RF by implementing the enhanced migration strategy; WaOA-RFMF, in turn, adds the improved fleeing strategy to WaOA-RFM. Finally, eWaOA integrates the gathering strategy into WaOA-RFMF. For performance evaluation, the following metrics are used for quantitative analysis in this section.

  • B(Cmax): the best makespan achieved across ten runs, assessing the optimal performance potential of algorithm.

  • Av: the average makespan over ten runs, indicating the algorithm’s overall performance.

  • Sd: the standard deviation of Cmax across ten runs, measuring performance of stability and consistency.

  • RPD (%): the relative percentage difference between the current algorithm and the best-performing algorithm, calculated as \(RPD = 100\% \times (C_{\max } - Min)/Min\), where Min is the smallest Cmax value obtained by all algorithms on the same test instance. A lower RPD value signifies closer proximity to the optimal solution and better search capability.

  • SdMean: the average Sd value for each algorithm across all test instances of varying sizes, reflecting the algorithm’s stability and consistency across different problem scales.

  • RPDMean: the average RPD value across all test instances of varying sizes, providing a comprehensive evaluation of the algorithm’s search capabilities across diverse problem scales.

Effectiveness of ROMI

To determine the optimal value for the “K” in the ROMI, experiments are conducted using the EMK05(s) benchmark. The “K” values range from 2 to 10, resulting in nine distinct experimental setups. The results, depicted in Fig. 6, show that when “K” is set to 7, the algorithm consistently achieves lower B(Cmax) and Sd values across the ten runs. Therefore, 7 is selected as the optimal parameter for the ROMI strategy. Figure 7 illustrates a detailed comparison of convergence processes for WaOA-R and WaOA, with walruses initialized by ROMI converging faster and more efficiently to a better makespan than those initialized randomly in WaOA.

Fig. 6
figure 6

Optimal selection of ROMI strategy parameter “K”.

Full size image
Fig. 7
figure 7

Convergence for two initialization strategies in EMK05(s).

Full size image

Table 5 presents the comparative experimental results of WaOA-R and the original WaOA across 30 test instances. The comparison reveals that incorporating the ROMI strategy improves B(Cmax) in 25 instances, with 1 instance yielding identical results and only 4 instances performing worse. For Av, improvements are observed in 28 instances, with only 2 instances performing worse. Regarding the Sd metric, 22 instances show improvement, and 8 instances perform worse. These comparisons, illustrated in Table 5 and Fig. 7, suggest that WaOA-R with the ROMI strategy not only demonstrates superior search capability but also exhibits improved stability and consistency compared to WaOA, while further enhancing the algorithm’s convergence efficiency.

Table 5 Comparison between WaOA-R and WaOA.
Full size table

Comparative experiments with enhanced WaOA variants

To validate the effectiveness and advantages of the enhanced feeding, migration, and fleeing strategies and the proposed the gathering strategy, we compare the metrics B(Cmax), Av and Sd across ten runs for the algorithms WaOA-R, WaOA-RF, WaOA-RFM, WaOA-RFMF and eWaOA. The experimental results are detailed in Table 6.

Table 6 Results obtained by different WaOA variants.
Full size table

Table 6 shows that WaOA-RF surpasses WaOA-R in terms of B(Cmax) for 20 out of 30 test instances, with 8 instances achieving identical results and only 2 instances showing slightly lower performance. For the Av metric, WaOA-RF demonstrates superior performance in 25 instances compared to WaOA-R, while 5 instances exhibit relatively lower Av values. Regarding the Sd metric, WaOA-RF outperforms WaOA-R in 17 instances, with 13 instances exhibiting comparatively higher Sd values. These results suggest that incorporating Lévy flight into WaOA’s feeding strategy enhances both makespan and solution stability. The key benefit of Lévy flight is its combination of short- and long-distance moves, which enables more effective exploration of the search space and better balance between exploration and exploitation.

The comparative analysis between WaOA-RFM and WaOA-RF highlights a significant performance improvement due to the enhanced migration strategy. For the B(Cmax) metric, 24 test instances show notable improvement, with 2 instances experiencing a minor decline and 4 remaining unchanged. Similarly, in the Av metric, 28 test instances demonstrate performance gains, while only 2 show slight declines. Regarding the Sd metric, WaOA-RFM outperforms WaOA-RF in 25 instances, with 5 instances exhibiting relatively higher Sd values. These findings underscore the enhanced migration strategy’s effectiveness in achieving an optimal makespan, along with improved stability and consistency. This improvement is likely due to the self-adjusting factor in the migration strategy, which promotes global exploration in early iterations and strengthens local exploitation in later stages.

Comparing WaOA-RFMF with WaOA-RFM reveals that the enhanced fleeing strategy positively impacts WaOA. Specifically, for the B(Cmax) metric, 21 test instances show performance gains, 6 instances experience slight declines, and 3 instances remain unchanged. In the case of the Av metric, 27 test instances show improvements, while only 3 instances perform worse than with the original fleeing strategy. For the Sd metric, 23 instances show improvements, while 7 instances perform relatively worse. These results conclusively demonstrate that the fleeing strategy with arctangent function-controlled local bounds significantly outperforms the original strategy, enhancing makespan, maintaining algorithmic consistency and stability, and reducing variability across runs.

Table 6 shows that eWaOA significantly improves the B(Cmax) metric in 27 test instances compared to WaOA-RFMF, with performance in the remaining 3 instances being comparable. This result robustly demonstrates eWaOA’s potential in global optimization. Additionally, eWaOA consistently improves the Av metric across all test instances. For the Sd metric, eWaOA achieves lower values in 28 instances, with 1 instance showing the same value as WaOA-RFMF, and only 1 instance showing a minor 0.1 increase. These findings strongly indicate that the gathering strategy significantly enhances WaOA’s ability to achieve a globally optimal makespan while markedly improving stability and consistency across multiple executions and diverse test scenarios.

The evolutionary trajectories of these algorithms on EMK09(s) are analyzed to assess whether the refined strategies accelerate WaOA’s convergence, as illustrated in Fig. 8a. This figure demonstrates that each improvement, relative to the baseline (WaOA-R), enhances convergence speed and achieves a better makespan. As shown in Fig. 8b, Curve 1, representing the difference between WaOA-RF and WaOA-R, displays fluctuations in the early and middle iterations, suggesting that Lévy flight significantly enhances WaOA’s global exploration capabilities. In the later stages, the differences in results continue to increase until reaching stability, indicating that Lévy flight also strengthens exploitation in the middle and later iterations, allowing the algorithm to escape local optima through occasional long-distance moves.

Fig. 8
figure 8

The diversity curves for the five algorithms to solve EMK09(s).

Full size image

Curve 2, representing the difference between WaOA-RFM and WaOA-RF, oscillates above the baseline with a broader range of values than Curve 1 during the early and middle stages. This pattern indicates that the enhanced migration strategy strengthens WaOA-R’s global exploration through the introduced adaptive parameter. In the middle and later stages, the differences continue to increase, reaching values significantly higher than those of Curve 1. This trend demonstrates that the adaptive parameter also facilitates more effective local search guidance.

Curve 3, which represents the difference between WaOA-RFMF and WaOA-R, shows pronounced fluctuations in the early and middle stages before transitioning into a phase of steady, stepwise improvement. Notably, Curve 3 consistently remains above Curve 2 throughout the process. This suggests that introducing the arctangent function to replace the inverse proportional function in the fleeing strategy does not diminish the global exploration capability provided by the enhanced feeding and migration strategies. Instead, it further enhances WaOA’s local search capacity in the middle and later stages. This improvement is mainly attributed to the extended global search range produced by the combined effect of the three enhanced strategies in the early and middle stages. The arctangent function expands the local bound, enabling the algorithm to perform more detailed local searches within a larger search space, thereby enhancing solution optimization in the later stages.

The combined application of all three enhanced strategies substantially improves WaOA-R's exploration and exploitation capabilities, leading to a reduced makespan. However, results indicate that WaOA still risks becoming trapped in local optima, with local search improvements progressing slowly during the middle and later stages. The proposed gathering strategy effectively addresses this issue. As shown in Fig. 8b, Curve 4, representing the difference between eWaOA and WaOA-R, remains consistently above Curve 3 throughout the process. Alongside Fig. 8a, it is clear that the algorithm demonstrates strong global search capabilities, leading to a rapid reduction in makespan and producing significantly better results than WaOA-RFMF in the early and middle stages. In the mid-to-later stages (e.g., after 75 generations), the stepwise increases in Curve 4 occur more frequently than in Curve 3, stabilizing around 200 iterations. Overall, the gathering strategy significantly enhances both exploration and exploitation in WaOA. The primary advantage of the gathering strategy lies in its random pairing of agents for positional information exchange, which prevents excessive concentration in specific regions and reduces the risk of becoming trapped in local optima. As iterations progress into the middle and later stages, shared positional information among paired agents converges, allowing individuals to refine their positions within localized areas. This process enhances both convergence speed and solution accuracy.

Figure 9 depicts the variation in the value of A according to Eq. (26) over iterations when solving EMK09(s), showing that in the early stages, the gathering strategy is highly likely to be employed, thereby enhancing WaOA’s exploration capability. Conversely, in the middle and later stages, the probability of using the gathering strategy decreases, shifting the focus toward improving exploitation. Thus, this strategy effectively balances exploration and exploitation throughout different phases. Figure 10 shows the Gantt chart for EMK09 (d), generated using the eWaOA algorithm. The chart illustrates that all operations comply with both the sequential order constraints of the process plan and the PBPO requirements. This demonstrates that the proposed methods for encoding, conversion, inverse conversion, and decoding effectively can handle the constraints of FJSP_PBPO.

Fig. 9
figure 9

The value of A over iterations of a run while solving EMK09(s).

Full size image
Fig. 10
figure 10

Gantt chart of a scheduling scheme for EMK09 (d).

Full size image

Comparative experiments with other metaheuristic algorithms

Due to the novelty of FJSP_PBPO, there are no publicly available algorithms for direct comparison. Meanwhile, the eWaOA proposed in this study is a standalone algorithm rather than a hybrid one. Therefore, this study selected 11 SOTA standalone metaheuristic algorithms for evaluation. Each algorithm uniformly employs the encoding scheme, conversion scheme and semi-active decoding method. The main differences among the algorithms lie in their initialization and iterative processes. These algorithms can be categorized into four groups: evolutionary-based, swarm-based, physics-based, and human-based. Evolutionary-based algorithms mimic natural evolution using selection, crossover, and mutation to optimize solutions. The GA and DE69, renowned for their robust global search capabilities, are the most prevalent evolutionary-based algorithms. They are widely applied in scheduling optimization and are chosen as comparison algorithms for this study. Swarm-based metaheuristic algorithms are developed by modeling the collective behaviors seen in natural phenomena. This study compares classic swarm-based metaheuristic algorithms, including PSO44 and GWO51, alongside newer algorithms such as HHO56, artificial rabbits optimization (ARO)70, and the latest WO12. Physics-based algorithms utilize principles from physics to address optimization challenges. In this paper, multi-verse optimization (MVO)71 and optical microscope algorithm (OMA)75 are chosen as comparison algorithms within the physics-based category. Human-based algorithms, inspired by human cognitive processes and behaviors, are represented here by the teaching learning based optimization (TLBO)76 and poor and rich optimization (PRO)72. To eliminate variations from differences in initial candidate solutions, enhance the repeatability and stability of the experiments, and ensure fairness and consistency in evaluation, the initial population size is uniformly set to 200. Other parameters are configured according to the default settings of each algorithm, with the specific values presented in Table 7.

Table 7 Parameter settings for the comparison algorithms.
Full size table

To comprehensively evaluate the performance of the algorithms across 30 extended test instances, we conducted two experiments: one with a fixed maximum number of iterations (Experiment 1) and the other with a time-limited termination criterion, where the algorithms terminate once the time limit is reached (Experiment 2). These experiments assess each algorithm’s capability to find the global optimal solution and its trade-off between solution quality and search efficiency. We compare the metrics B(Cmax), Av, Sd, RPD, SdMean, RPDMean for all 12 algorithms.

The results of Experiment 1 are presented in Table 8. Notably, eWaOA achieves optimal values for the B(Cmax), Av, and PRD metrics across all 30 test instances. Specifically, eWaOA attains optimality in 26 instances for B(Cmax), while in the remaining 4 instances, it ties with other top algorithms. For the Av metric, eWaOA achieves optimality in all 30 instances. Furthermore, among the 12 algorithms, eWaOA records the lowest Sd value in 22 of the test instances. In terms of SdMean and RPDMean metrics across all instances, eWaOA demonstrates superior performance with values of 3.3 and 0, respectively. Table 9 presents the termination time settings (Time) and the results of Experiment 2. As shown, eWaOA also demonstrates strong competitiveness. Specifically, eWaOA achieves the minimum values for the B(Cmax), Av, and Sd metrics in 28, 30, and 15 instances, respectively. Notably, eWaOA also performs well in the SdMean and PRDMean metrics, with the lowest values of 3.9 and 0.1, respectively. These results indicate eWaOA’s efficient optimization capability within a fixed termination time.

Table 8 Comparison results with the same maximum number of iterations.
Full size table
Table 9 Comparison results with identical time-limited termination.
Full size table

For each algorithm, we select the iteration data with the minimum Cmax from 10 runs and then plot the Cmax variation curves for different test instances, as shown in Fig. 11. In this figure, eWaOA attains the lowest Cmax in all 30 instances. Moreover, the eWaOA achieves better Cmax values with significantly fewer iterations (less than 50) for instances like EMK01(s), EMK01(d), EMK03(s), EMK04(s), EMK04(d), EMK05(s), EMK08(s), EMK08(d), EMK14(s), and EMK14(d). For instances EMK03(d), EMK05(d), EMK07(s), EMK11(d), EMK12(s), and EMK12(d), the convergence curve of eWaOA stabilizes within 50–100 iterations. For instances EMK02(s), EMK07(d), EMK09(s), EMK09(d), EMK13(d), EMK15(s), and EMK15(d), convergence stability is achieved within 100–200 iterations. For instances EMK02(d), EMK06(s), EMK06(d), EMK10(d), EMK11(s), and EMK13(s), stability is achieved before 250 iterations.

Fig. 11
figure 11figure 11

Iterative results of various algorithms for solving FJSP_PBPO instances.

Full size image

To highlight the remarkable advantages of eWaOA over other algorithms, a paired t-test was conducted at a significance level of α = 0.05 to explore the existence of statistically significant differences between eWaOA and various comparative algorithms. The data for this paired t-test were obtained from the outcomes of running eWaOA and each comparative algorithm 10 times per instance. Figure 12 shows the results of the paired t-test regarding the Cmax of eWaOA and comparative algorithms for each test instance. In this figure, each group on the x-axis represents the paired t-test results of eWaOA against a specific comparative algorithm, and the log2FC shown is calculated based on the average values of Cmax. Specifically, we first determine the fold change of the average Cmax of eWaOA compared to that of each comparative algorithm and then take the logarithm to the base 2 of this fold change. Moreover, according to the p-values from the paired t-test, the scatter points in the graph are divided into two groups: the group with a “p-value ≤ 0.05” is represented by red scatter points, indicating a statistically significant difference, while the group with a “p-value > 0.05” is shown by blue scatter points. To avoid complete horizontal overlap of data points and improve the readability of the scatter plot, random perturbations have been applied to each data point during the plotting process. As can be seen from the figure, except for the EMK14(d) instance in the comparison between eWaOA and ARO, and the EMK07(d) instance in the comparison between eWaOA and TLBO, eWaOA shows highly significant differences from other algorithms in most instances, as demonstrated by the distribution of red and blue scatter points as well as the values of log2FC.

Fig. 12
figure 12

The results of the paired t -test between eWaOA and the other 11 SOTA algorithms for the 30 test instances.

Full size image

Based on the results in Tables 8 and 9, as well as Figd. 11 and 12, we conclude that the proposed eWaOA significantly outperforms the 11 SOTA algorithms in both optimization effectiveness and efficiency. Specifically, eWaOA demonstrates superior performance in terms of makespan, stability, consistency, and optimization efficiency-achieving better results within the specified time.

Engineering case study

This study aims to further validate the proposed eWaOA by applying it to a practical engineering scenario involving three distinct product categories tested at an electronic product performance lab. The products include mobile phones (MP), in-vehicle navigators (IVNs), and unmanned aerial vehicles (UAVs). The performance testing process plan for MP is illustrated in Fig. 1, while the testing process plan for IVNs and UAVs are detailed in Tables 10 and 11, respectively.

Table 10 Process plan of the IVNs.
Full size table
Table 11 Process plan of the UAVs.
Full size table

The results obtained by applying the 12 algorithms to the engineering case are presented in Table 12. All algorithms use an time-limited termination criterion, with the corresponding time limit set to 55(s). It is evident that PSO, GWO, ARO, TLBO, and eWaOA yield the smallest B(Cmax), with eWaOA achieving the lowest Av and Sd. This further demonstrates that eWaOA not only minimizes B(Cmax) but also shows superior stability and consistency. Figure 13 displays the Gantt chart of the optimal scheduling results from 10 runs of eWaOA, with PBPOs highlighted in red boxes. The chart demonstrates that all operations adhere to the sequential order constraints of the process plan and satisfy the PBPO requirements, reaffirming the feasibility and effectiveness of eWaOA in solving the FJSP_PBPO.

Table 12 Comparison of scheduling results for instance from testing workshop.
Full size table
Fig. 13
figure 13

Gantt chart of a scheduling scheme obtained by eWaOA for the practical example.

Full size image

Conclusion and future research

To optimize the makespan for the FJSP_PBPO problem, this study develops an optimization model using MIP and introduces an enhanced swarm-based metaheuristic algorithm, eWaOA, which extends the WaOA framework. In eWaOA, new schemes for encoding, conversion, inverse conversion, and decoding tailored to the specific constraints of FJSP_PBPO are designed. Additionally, a ROMI strategy is designed to generate diverse and high-quality initial solutions. Enhancements are made to the feeding, migration, and fleeing strategies of WaOA, and a novel gathering strategy is introduced to improve both exploration and exploitation.

To evaluate these improvements, 30 test instance, extended from existing benchmark FJSP instances, are used. The ROMI initialization strategy shows superior search capability, stability, and consistency compared to WaOA, enhancing convergence efficiency. Comparisons are made with four enhanced WaOA variants and eleven SOTA metaheuristic algorithms on the 30 test instances, followed by a real-world engineering case study. Results from these comparisons confirm that the eWaOA effectively addresses the FJSP_PBPO, demonstrating superior optimization capability, stability, consistency, and efficiency.

The proposed eWaOA primarily addresses the FJSP with PBPO. However, electronic product performance testing introduces additional constraints, including multi-resource coupling and sequence-dependent setup times. Future research will focus on enhancing eWaOA to effectively handle these constraints, extending its applicability to more complex engineering scenarios.